一道矩形翻折问题的拓展与思考

深圳实验学校初中部 秦 哲 （邮编：518028）

矩形的翻折问题一直被用作中考填空或选择压轴题，学生遇到这类问题常常无法将已知条件和数学知识建立联系，更不知从哪方面进行突破. 现借助一道矩形翻折问题的变式拓展，帮助学生熟悉“数学模型”，引导学生从不同角度分析问题，帮助学生内化解决数学问题的方法和技巧，进一步探索如何帮助学生提高解题能力.

1 例题讲解

例题如 图1，在 矩形ABCD中，AB=4，BC=6，点E为BC的 中 点，将△ABE沿AE折叠，使点B落在矩形内的点F处，连接CF，求CF的长.

图1

简解如图2，连接BF交AE于点K，点F由点B翻折所得，则AE垂直平分BF于点K，故∠AKB=90°. ∠ABE=90°，则∠1+ ∠ABK=∠2+∠ABK=90°，故∠1=∠2.AB=4，BE=3，易得因EF=EC=BE=3，在Rt△BFC中

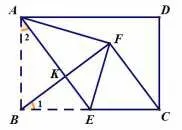
图2

分析本由EF=EC=EB形成的直角三角形BFC，将求线段CF的长转化为“解直角三角形”. 由“翻折”的性质得到垂直，再由已知直角（∠ABE=90°），得到常见的“双垂直模型”（∠ABE=∠BKA=90°），其常用的结论是“三组直角三角形相似”和“角的等量关系”，本题也可以利用△ABE∽△BFC进行求解.

变式训练1 如图3，连接BF并延长BF交线段AD于点G，求线 段FG的长. 因AD∥BC，则∠1=在Rt△AGB中，AB=4，则在

图3

2 变式训练

变式训练2. 如图4，延长EF交线段AD于点G，求线段FG的长.

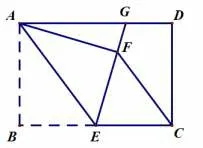
图4

分析将问题变式的出发点是想让学生体会“角 平 分 线”“平 行”和“等腰三角形”在矩形翻折问题中的应用，这里称之为“角平分线平行模型”（解题过程详见方法1）. 正所谓“无心插柳柳成荫”，在现实的课堂教学中，学生透过不同角度思考，一共想出了8 种解题方法，而这些方法都涉及到平面几何中常用的解题技巧和思路.

2.1 解法归纳

方法1 “角平分线平行模型”

如 图5，因△AFE由△ABE翻折所得，则∠1= ∠2. 因AD∥BC， 得∠2=∠EAD，故∠EAD= ∠1，则GE=GA. 设GF=x，AG=GE=3+x，AF=4，在Rt △AFG中，AF2+FG2=AG2，则42+x2=(3+x)2，解 得

图5

方法2等腰三角形“三线合一”的性质

方法3延长CF“8字型相似”

图6

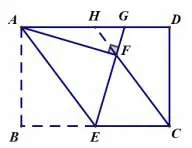
图7

方法4三角形相似（1）

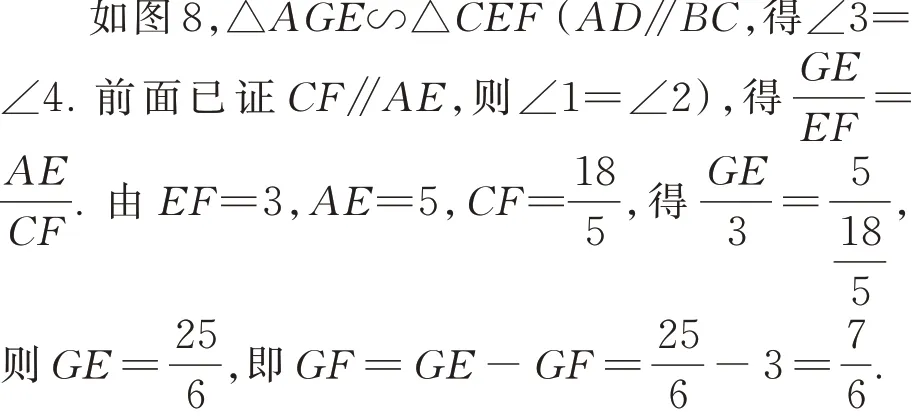
方法5三角形相似（2）

如图9，延长AF交CD于点H，连接BF. 前文已证∠BFC=90°，则∠FBC+∠FCB=90°，又∠FCB+ ∠FCH=90°，则∠FBE= ∠FCH. 因∠EFH= ∠HCE=90° ，则∠FHC+ ∠FEC=180°，因∠FEC+∠FEB=180°，则∠FEB=∠FHC，由此可得

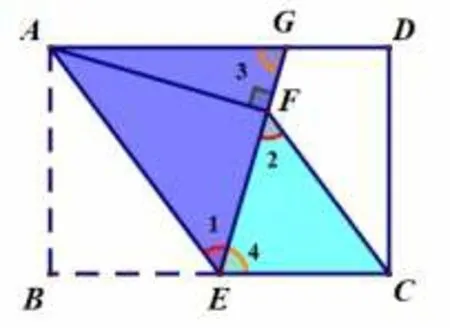
图8

图9

方法6 “斜化直”

方法7三角形全等

如图11，过点G作BC的垂线交BC于点H，易证四边形AGHB为矩形，则GH=AB=AF，∠AGH=90°. 由AG∥BH，得∠AGF=∠GEH，易证△AFG≌△GHE. 设GF=x，则GE=3+x，EH=GF=x，GH=AB=4. 在Rt △GEH中，EH2+GH2=EG2，则42+x2=(3+x)2，解 得

图10

图11

2.2 解题反思

对学生而言，能够在经历系统的数学学习和利用数学知识与方法解决特定情境中的问题后，通过体验、认识、内化成较为稳定的数学化地理解问题和解决问题的思维方式，也是数学素养中提到的重要标志之一[1]. 本文试图透过“一题多解”帮助学生总结矩形翻折问题中常用的“技巧”和“方法”，学生通过不同角度对问题进行整合产生的7 种解法，这看似独立又互相联系.

方法1 与方法2 的突破口在“等腰三角形”，学生通过角平分线和平行线产生的角度数量关系得到一组相等的角，进而得到的“等腰三角形”. 方法1 侧重于等腰三角形的“腰相等”，通过设未知数，利用勾股定理列方程求解；方法2 关注于等腰三角形的对称性，利用“三线合一”的性质求出相应的线段，再利用“三角函数”求解线段.

方法3、方法4 和方法5 利用相似进行求解，许多教师在教学中都会让学生熟记常见的“相似模型”，方法1 中已知EF，求GF，学生观察到AD∥BC，进而通过延长线段，构造常见的“8 字型”相似求解；在方法2 中，“几何直观”强的同学发现图中不需要添加辅助线便得到线段EF和线段GE所在的三角形相似（△AGE∽△CEF）进行求解；方法3 相对复杂，学生首先延长AF，想通过△AFG∽△ADH求解，而求DH则需要通过另一组相似△FHC∽FEB，此方法复杂，但这两组相似在解决线段问题中经常用到.

方法6 与方法7 则引出解决以矩形为背景的问题中最常见的方法：“斜化直”，本质上是通过作垂直构造直角三角形，利用直角三角形特殊的边角关系联系题目的已知条件进行求解. 由此，通过多种方法的总结与内化，我们发现：“角平分线平行模型”“三角形相似”和“斜化直”是解决矩形翻折问题重要的“突破口”.

4 拓展训练

变式训练3 如图12，在 矩 形ABCD中，AB=4，BC=6，点E为AB的 中 点，将△BEC沿EC折叠，使点B落在矩形内的点F处，连 接EF并延长交线段AD于点G，求AG的长.

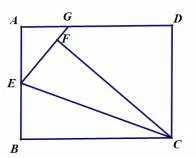
图12

4.1 解法归纳

为了检验学生是否将课堂中总结的方法和技巧内化为稳定的数学化理解问题和解决问题的思维方式，继续对例题进行变式，作为课后作业. 现将学生的解法整理如下.

方法1“斜化直”

如 图 13，连 接AF，过 点F作 线 段AD的垂线交线段AD于点M，交线段BC于点N，因为四边形ABCD是 矩 形，则AD∥BC，所以∠FNB=90°. 因EF=AE=BE，则∠AFB=90°，由 此易证：△AMF∽△FNB，这就是常见的“K 型图”相似模型. 翻折的性质可得EC⊥BF，再由∠EBC=90°，可得到前文提及的“双垂直模型”，易得，故△AMF与△FNB的相似比为1∶3，可 设 未 知数MF=a，则BN=3a，易 证AMNB为 矩 形，则AM=BN=3a，FN=9a，因MN=AB=4，则a+9a=4，即可得由MF∥AE，易证：△GMF∽△GAE，则即解 得

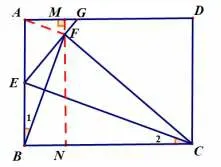
图13

方法4 “角平分线平行模型”

如图14，延长EF和CD交于点K. 由∠1= ∠2，AB∥CD，易 得KE=CK，设DK=x，则EK=KC=4+x. 因EF=2，则KF=EK－EF=4+x－2=2+x. 由翻折可得FC=BC=6，在Rt △KFC中，利 用“勾股定理”列方程，得62+(2+x)2=(4+x)2，解得x=6. 易证△AEG∽

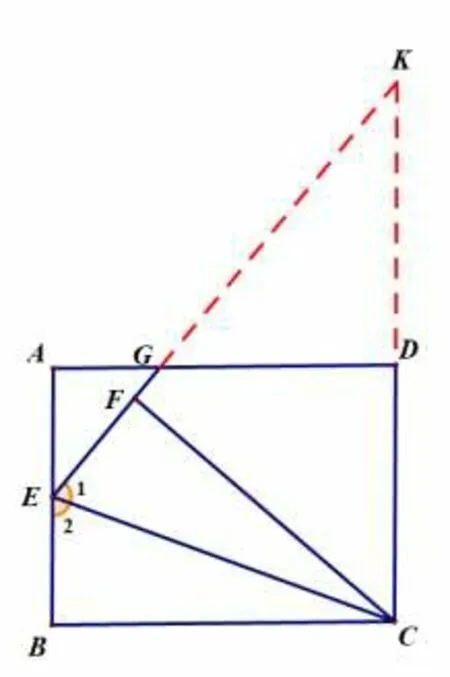
图14

方法3“倍角公式”

图15

因为∠B=∠EFC=90°，则∠FEB+ ∠FCB=180°，又∠1+ ∠FEB=180°，则∠1=∠FCB.在Rt△AEG中

4.2 解题反思

变式训练3 中，点E从线段BC的中点改为线段AB的中点，“沿着AE翻折”改为“沿着CE翻折”，虽对题目只是微小的变化，难度却有提升.

方法1 经由垂直构造“K 型图”的相似模型，利用相似比设未知数，通过矩形边的等量关系列出方程，求出线段，方法虽然复杂，计算量偏大，但学生最容易想到此方法解题；在变式训练2 中，仔细观察便能准确找到等腰三角形进行解题，而在变式训练3 中，等腰三角形却不易被发现，此时需要延长线段（如方法2），也就是在矩形外作辅助线，才能得到等腰三角形. 在教学中，笔者发现：学生在添加辅助线时倾向于在图形内作辅助线，特别不擅长通过“延长线段”或“旋转图形”，因此在教学中需提醒学生关注“在图形外作辅助线”；熟练掌握“倍角公式”的同学通过方法3 顺利解题.

课后与学生进行交流，总结他们在解题中的一些“弯路”：有学生连接BF，尝试寻找相似三角形进行求解，学生寻找到的相似三角形仅存在于四边形EFCB内，无法与矩形ABCD进行联系，解题失败；有学生延长GE和CB相交于点K，尝试求出∠AGE的三角函数，结果失败；又尝试利用Rt△FKC，希望通过勾股定理列方程，此时则分别对GF和BK设未知数，然而GF和BK无法继续找到等量关系进行消元，仍然无法求解.

在教学中，我们困惑于解题技巧和方法已经反复强调，然而学生还是不会，解题能力的提升并不是一蹴而就，它涉及到“几何直观”“分析与联想”等多方面的能力的协调发展和提高. 教学中仅仅是“方法”和“技巧”的传授远远不够，还需关注学生在解题中遇到的具体困难和失误，剖析解题失败的原因，培养他们通过“整体”分析问题，引导使用正确的“策略”解题.

5 反思与总结

从一道矩形翻折问题出发，进行变式，引导学生深入思考. 文中的方法相互联系，有的方法简便明了，有的方法稍稍复杂，各种方法都有重要的价值. 课堂中，笔者欣喜地看见学生踊跃发言，津津乐道于自己独特的解题方法，又常常为自己的“独到眼光”而感到自豪，教室中时常爆发出热烈的掌声.“一题多解”启发学生从不同角度思考问题，进而巩固“常见解法”和“基本技巧”，学生积极表达自己的想法，洋溢着自信的喜悦，极大地获得学习数学的兴趣，有效地发展学生的逻辑推理、数学建模等核心素养.

在教学中充分发挥学生的主观能动性，启发和训练学生的模型思想. 波利亚说：“解题的成功要靠正确的思路选择，要靠从可以接近他的方向攻击堡垒.[2]”这里的“方向”可以是平面几何中常见的“几何模型”，本文中运用的模型有：“双垂直模 型”“平 行 线 角 平 分 线 模 型”“K型 图”等；“方向”可以是题目中的特殊图形，如“等腰三角形”“三条边已知的三角形”等. 在教学中，提醒学生关注上述两点，积累解题经验，训练模型思想.

提升学生的解题能力，打通解题思路还需要帮助学生分解和整合题目的已知条件，帮助学生进行合理地联想，拓展学生的解题思维. 无论是哪种解法，其本质都是抓住题目中的条件特征，并对其进行分解和重组，多种解法的生成与诸多因素有关[3]. 多种解法的形成和巩固，有助于学生加深对解题方法的理解，更加大对解题技巧的熟练应用. 进一步深化学生对“数学模型”的理解.

《义务教育数学课程标准（2011 年版）》指出：数学思想蕴藏在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次的抽象与概括[4]. 前文已强调在平时的教学中需要训练学生的“模型思想”，若只关注数学模型的熟记和训练无异于“只见树木，不见森林”. 教师让学生关注解题常用的方法和技巧，分析各种解法后，还应该引导学生总结解法之间的共性，提炼解决一般问题的数学方法和思想.