指向数学核心素养的深度学习途径探究

浙江省临海市第六中学 陈冬菊 （邮编：317000）

浙江省临海市回浦中学 李昌湛 （邮编：317000）

在以提升学生数学核心素养为目标，以减轻学生学业负担为愿景的新课程背景下，教师要努力提高课堂效率，培养学生分析问题和解决问题的能力，开展深度学习是实现这一目标的有效途径．但笔者发现我们的课堂依然存在大量的浅表性学习和假性学习，那么，如何开展有效的深度学习？下面从四个方面进行阐述，不到之处请批评指正．

途径一 开展一题多解进行深度学习

一个数学问题往往有多种解法，每种解法都可以开拓学生的思路，融会贯通各知识和方法．一题多解让学生对问题进行多角度、多层次的深度学习，从中选择更快捷准确的最优解法，能培养学生思维的全面性和灵活性，从而提升学生数学核心素养．

案例一等差数列的前n项和Sn的最值问题

例1(多选)已知递减的等差数列的前n项和为Sn，若S7=S11，则（ ）

A.a10＞0 B.当n=9 时，Sn最大

C.S17＞0 D.S19＞0

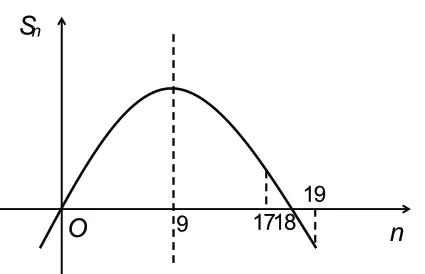
图1

途径二 设计变式教学进行深度学习

变式教学是通过变换数学问题的非本质特征来暴露本质特征的教学方法．变式教学能促进学生数学思想方法的内化，能培养学生的创造性思维，能培养学生思维的深刻性，从而提升学生数学核心素养．

在求解与圆锥曲线的中点弦有关的问题时，点差法是一种非常重要的方法，这种方法能较好体现解析几何的设而不求思想，为了更好地深化这类问题，下面以椭圆为例设计变式教学．

例2如图2，已知椭圆b＞0)，斜率为k1的直线交椭圆于A、B两点，若点M是线段AB的中点，O是坐标原点，且直线OM的斜率为k2，求k1·k2的值．

图2

解析设 点A(x1，y1)，B(x2，y2)，M(x0，y0)，两式作差可得

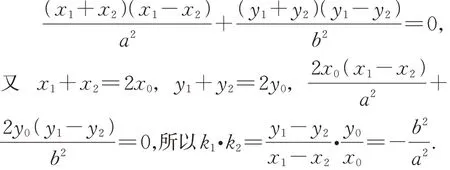
这一性质看似简单，但应用广泛，高考试题经常涉及这一性质，值得深化学习，所以可设计下面的变式进行深度学习．

变式1如图3，已知A、B是 椭 圆1(a＞b＞0)上关于原点O对称的两点，P是椭圆上任意一点，且直线PA、PB的斜率分别为k1、k2，求k1·k2的值．

图3

解析取AP的中点M，连接OM，因为O是AB的中点，所以OM//PB，那么此题就变成例2 的问题了，由例2 知

变式2如图4，过椭圆b＞0)上任意一点P（不是椭圆的顶点）作椭圆的切线，设切线的斜率为k1，O是坐标原点，直线OP的斜率为k2，求k1·k2的值．

糖尿病为临床多发疾病,是一种慢性消耗性疾病类型,以老年患者作为常见人群,该疾病的发病因素主要与不良饮食习惯和生活方式、遗传因素、环境因素等密切相关[1]。该疾病的常见表现为血糖水平异常上升,对患者的生活质量和身心健康均造成不利影响。而控制血糖为治疗该疾病的主要目标[2]。本院对阿卡波糖对社区糖尿病患者的治疗效果及安全性进行分析,并总结分析结果(2016至2017年),具体情况见下文描述。

图4

解析如图2，事实上利用极限的思想，当AB往外平移至与椭圆相切时，则A、B、M三点重合于切点P，所以仍然有

教师还可以对双曲线设计类似上面的变式教学，另外，上面的问题都是针对焦点在x轴上的椭圆或双曲线，我们还可以设计焦点在y轴上的椭圆或双曲线的变式教学，问学生结论还会一样吗？通过这样的变式开展圆锥曲线的中点弦问题的深度学习，效果比较好．

途径三 制作微课进行深度学习

微课具有内容短小精悍、能重复使用、能激发学生学习兴趣等特点．实践证明微课取得了实质性的教学效果．教师可利用微课这种新的教学手段针对某个知识点开展深度学习．

案例三空间轨迹问题的求法

空间的轨迹问题图形抽象，对学生的空间想象能力要求高，并且求解方法多样，对学生来说是个难点．这时，可制作微课《空间轨迹问题的求法》开展深度学习，突破这一难点，学生兴趣很高，教学效果良好．

例3如图5，在正方体ABCD－A1B1C1D1中，P是侧面BB1C1C内一动点，若P到直线BC的距离与到直线C1D1的距离相等，则动点P的轨迹所在的曲线是（ ）

图5

A. 直线 B. 圆 C. 双曲线 D. 抛物线

解析在正方体中，易知直线C1D1⊥平面BB1C1C，所以C1D1⊥PC1，所以PC1就是点P到直线C1D1的距离，那么，点P到直线BC的距离等于它到点C1的距离，根据抛物线的定义，点P的轨迹是抛物线，故选D．本题利用抛物线的定义得出所求轨迹的形状，这是求解空间轨迹问题的第一种方法——定义法．

例4如图6－1，平面α的斜线AB交平面α于点B，且与平面α成60°，平面α内一动点C满足∠BAC=30°，则动点C的轨迹所在的曲线是（ ）

A. 直线 B. 圆

C. 椭圆 D. 双曲线的一支

解析 因为∠BAC=30°，所 以直线AC绕着轴AB旋转形成的图形是圆锥的侧面，又因为动点C在平面α内，所以，原问题相当于用一个与轴成60°的平面去截圆锥的侧面，那么得到的轨迹是椭圆，如图6－2 所示．故选C．本题利用不垂直于轴的平面截圆锥截口曲线的形状的结论得出答案，这是求解空间轨迹问题的第二种方法——几何法．

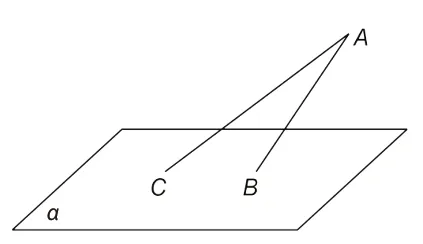
图6 -1

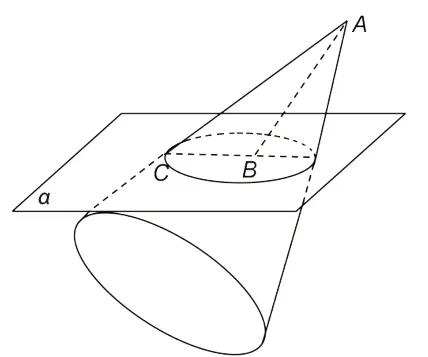
图6 -2

7）图7

例5如图7，已知正方 体ABCD－A1B1C1D1的棱长为1，点P是平面ABCD上的动点，若点P到直线A1D1的距离等于点P到直线CD的距离，则动点P的轨迹所在的曲线是（ ）

A. 抛物线 B. 双曲线 C. 椭圆 D. 直线

利用以上三个例题制作的微课内容精简，主题突出，能使学生较好地掌握空间轨迹问题的三种典型求法：定义法、几何法和代数法．

途径四 组织小组合作学习进行深度学习

小组合作学习可以提升课堂的活跃程度，能引发学生的深层思考，能培养学生的主动参与意识．小组合作学习形成了师生、生生之间的全方位、多层次、多角度的交流模式，是进行深度学习的一种重要方式．

案例四四点共面问题

例6如图8，在四棱锥P－ABCD中，ΔPAD是以AD为斜边的等腰直角 三 角 形，BC∥AD，AB⊥AD，AD=2AB=2BC=2，PC= 2，E、F

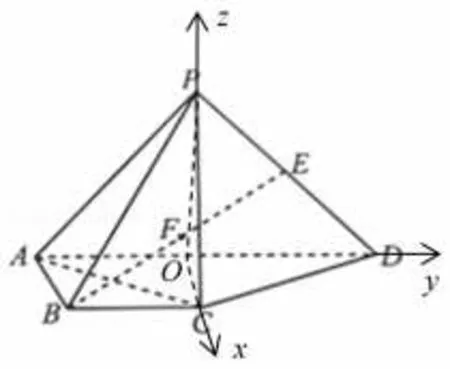
图8

分别为线段PD、BE的中点．判断点F是否在平面PAC内，并证明你的结论．