野战火箭炮装填系统柔性机构多目标拓扑优化

葛世程,郭着雨,梁熙,莫宗来,李军

(南京理工大学 机械工程学院,南京 210094)

野战火箭炮的快速再装填是提高火箭武器打击效能的主要研究方向之一。相较于传统的绳索装填和刚性装填技术,新兴的柔性装填系统利用柔性机构的柔顺性在发射箱的对接、起吊、转运和落装过程中拥有较好的综合性能。其中,柔性机构需要同时满足空载工况下的刚度及负载工况下的柔度,在保证准确空间位置的同时保证柔顺性。结构是影响柔性机构工作性能的关键因素之一,因此对柔性机构的多目标结构优化有较为深入的研究[1-4]。

拓扑优化是一项在特定区域内寻找满足一定约束条件下的最佳材料分布的技术。其起源于Michell在1904年提出的桁架结构优化设计理论,但其属于离散结构拓扑优化,对一般问题的描述较差[5-6]。为了增强拓扑优化的一般性,以均匀化方法和变密度法为代表的连续体结构拓扑优化技术得以快速发展[7-8]。例如轻量化设计,在保证静态刚度和动态刚度的同时有效降低了质量,在运输工业特别是航空航天领域得到了高度重视[9-10]。

然而对于柔性机构,优化目标通常不以质量为首要目标,而是关注结构的刚度分配。例如在轴孔装配领域,柔性机构需要在轴向保持较高的刚度并提高径向的柔度从而提高其引导装配的能力[11-12]。再如在微型柔性机构研究中,需要结构整体的柔度最小,同时提高输出端的位移[3]。为了满足柔性机构的多目标设计要求,使用折衷规划法、物理规划法和线性加权法等多目标优化方法建立拓扑优化目标函数,对柔度、输出位移和模态等性能进行多目标优化的技术得到较为广泛的应用[1-3,13-14]。然而对于空载工况下需要的整体结构刚度和负载工况下的整体结构柔度的多目标优化未见深入研究报道。

综上所述,针对柔性机构空载工况下的刚度和负载工况下的柔度要求,以SIMP方法为拓扑优化方法,采用折衷规划法定义静态刚度和动态振动频率的多目标优化函数。进一步借助HyperWorks软件中的OptiStruct拓扑优化模块对柔性机构进行多工况下的多目标拓扑优化。优化后,利用Abaqus软件对优化结果进行检验,以期获得满足野战火箭炮装填要求的柔性机构。

1 多目标拓扑优化方法

1.1 SIMP法

拓扑优化中的变量根据性质可分为物理变量和材料变量。变密度法引入了一系列与离散单元对应的人工密度,变化范围为[0,1],并构建人工密度与其依附的离散单元的物理属性(如体积和弹性模量)的关系实现离散单元在整体结构中的“有无变化”。变密度法中变量的连续变化大大方便了数学求解但不可避免的带来了中间密度,既实际中不存在的的单元。为了避免中间密度,Sigmund等提出了SIMP法,通过引入惩罚因子对中间密度值进行惩罚使其向0和1逼近[15]。以结构柔顺度最小为目标函数,体积为约束条件,单元密度为变量的SIMP拓扑优化模型如下:

(1)

式中:C(x)为结构柔度用应变能定义,x为设计变量的向量;p为惩罚因子;f为规定的体积分数。

惩罚因子作为SIMP法的关键参数,当p>1但较小时惩罚效果差,随着的p增大则边界越清晰,但过大的p容易丢失最优结构。为了保证惩罚效果和获得最优结构,对于壳单元p通常取3,对于体单元p通常取2[16]。解决中间密度后仍存在棋盘格问题和网格依赖性等数值不稳定现象,为此通常需要结合其它方法进行补充。例如敏度过滤法、周长约束法和下限约束法等,通过建立单元与相邻单元的关系和限制条件来消除数值不稳定现象[17]。

本文采用Altair公司的OptiStruct软件对柔性机构进行拓扑优化。OptiStruct软件的材料模式采用SIMP方法,同时采用下限约束法和周长约束法限制数值不稳定现象,并采用数学规划方法作为优化算法[18]。

1.2 多目标优化方法

拓扑优化中的优化目标主要分为响应类和载荷类。响应类目标根据零件的性能指标分为刚度,质量和固有频率等,载荷类目标根据零件的载荷情况进行分类,进而得到不同工况下的目标值。对于目标间有交互影响的多目标问题的处理方法以将其转为单目标问题为主,进而获得满足多个目标的有效解(或Pareto解)。这里主要介绍加权系数法和折衷规划法[3,19]。

1) 加权系数法

对于只有载荷类目标的多目标问题,无需考虑目标间的单位不同带来的影响。加权系数法通过给定目标的权值可以将多目标问题转为单目标问题,适用于只有载荷类目标的多目标问题。加权系数法模型如下:

(2)

2) 折衷规划法

响应类和载荷类目标同时存在时,目标函数间的差异会产生不可靠的优化结果。对此,功效系数法根据多目标规划原理,对函数值进行无量纲化。其中线性功效函数为

(3)

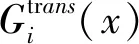
为了得到尽可能满足各个目标函数的Pareto解,一种折衷方法定义如下

(4)

式中：n(x)为多个目标函数合成的单目标函数;p≥2。

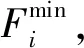
(5)

2 柔性机构及其工作原理

柔性装填系统方案如图1所示,吊臂和吊装平台提供装填的6个自由度运动,用于控制安装在吊装平台上摆动柔顺式吊钩完成发射箱装填的对准、对接、起吊、转运、落装和脱钩这6个步骤。具体工作过程如下:吊装平台运动至发射箱上部并对准对接位置,对准后吊装平台进行U型运动完成对接;对接完成后顺势起吊发射箱并将其转运至发射车上方使发射箱底部定位孔对准发射车上的定位销;吊装平台向下运动,发射箱在重力的作用下完成落装后吊装平台进行U型运动完成脱钩。

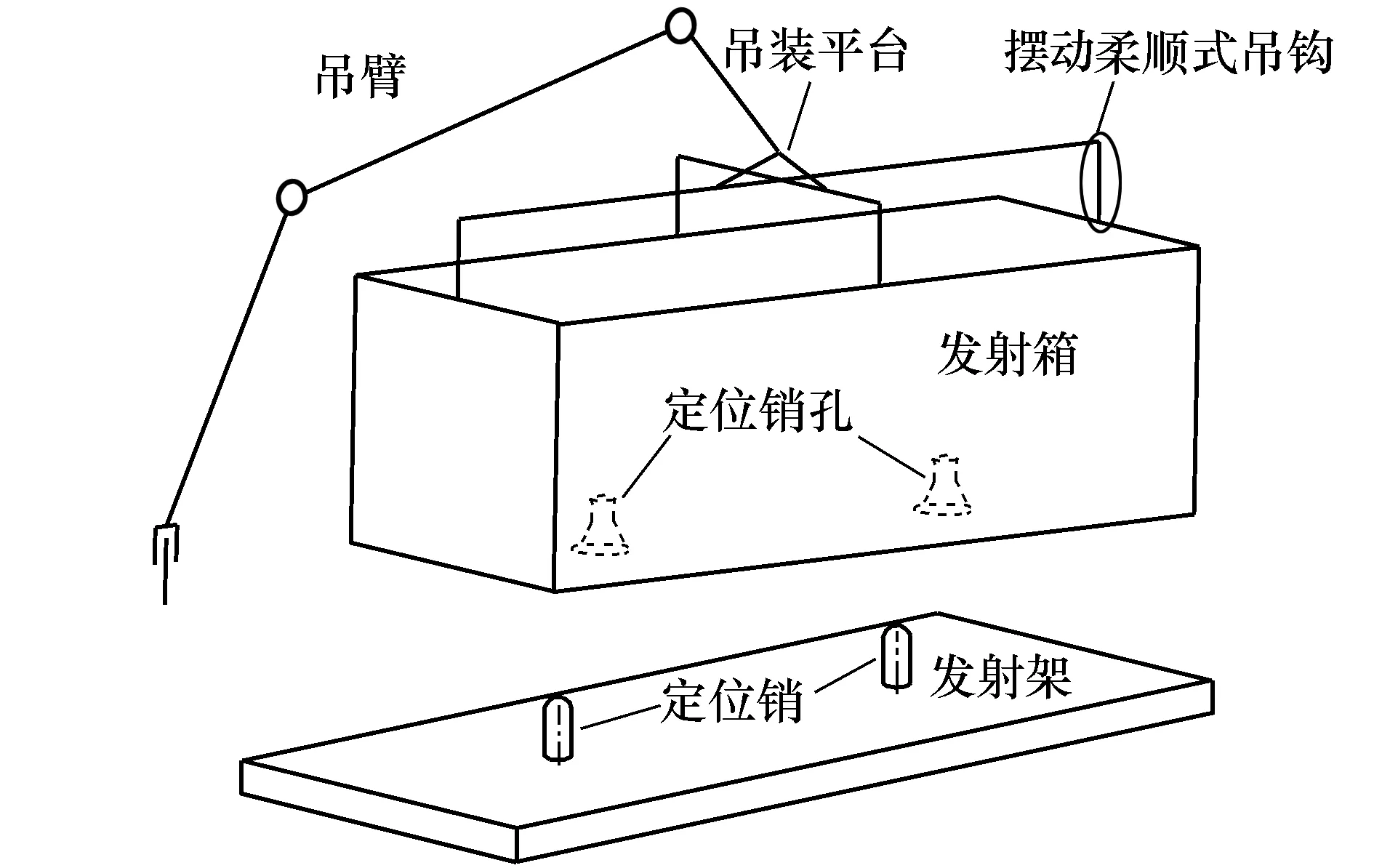
图1 柔性装填系统方案

如图2所示,摆动柔顺式吊钩通过定支座固定在吊装平台上,定支座、动支座和吊钩形成二自由度虎克铰链,柔性机构分别与定支座、动支座和吊钩联接,用于限制吊钩的二自由度摆动。快速和倾斜地形装填(与水平面最大倾角为5°)是柔性装填系统的两个主要性能要求。

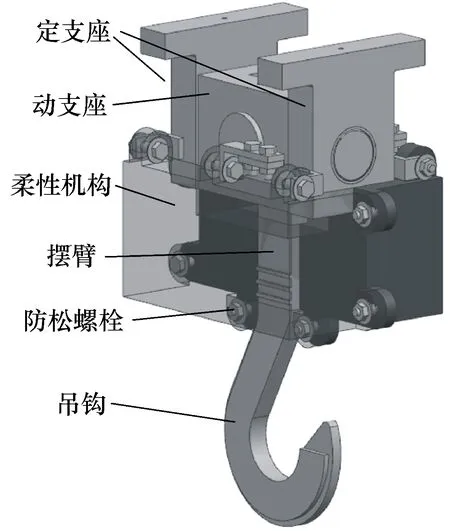
图2 摆动柔顺式吊钩几何模型

摆动柔顺式吊钩对准发射箱的过程为空载工况,如图3a)所示,需要柔性机构拥有良好的静态刚度和动态刚度,以限制吊钩相对吊装平台的位移及缩短稳定时间。摆动柔顺式吊钩转运发射箱的过程为负载工况,如图3b)所示,需要柔性机构有良好的柔度使吊钩相对吊装平台的位移最大既吊钩受力点连线在重力方向上。可以看出,柔性机构空载工况下的刚度和负载工况下的柔度是以吊装平台位姿确定吊钩和发射箱位姿的前提。

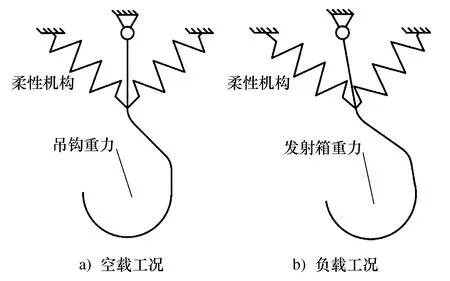
图3 柔性机构工作原理

为了保证射击密集度,发射箱在发射车上的位置由配合精度较高的定位销和定位孔确定。由于柔性机构的设置在一定程度上降低了精度要求,本文取空载工况下吊钩相对吊装平台的最大角位移为1°,负载工况下吊钩与重力方向的最大角偏差为1°。

3 拓扑优化模型

3.1 有限元模型

1) 模型简化

本文涉及的工况较多,且需要计算柔性机构前四阶频率,为了减少计算量,如图4所示,对柔性机构进行简化,将动支座和吊钩用一维单元表示。为了避免非线性的接触分析,将原有的两个柔性机构合并。进一步地,上表面用于联接的螺栓简化为点A1,A2,B1,B2,C1和C2,并通过rigids单元与对应的螺栓联接凸台内壁联接。柔性机构与吊钩的接触简化为点D,并通过rigids单元与柔性机构下端的内壁联接。

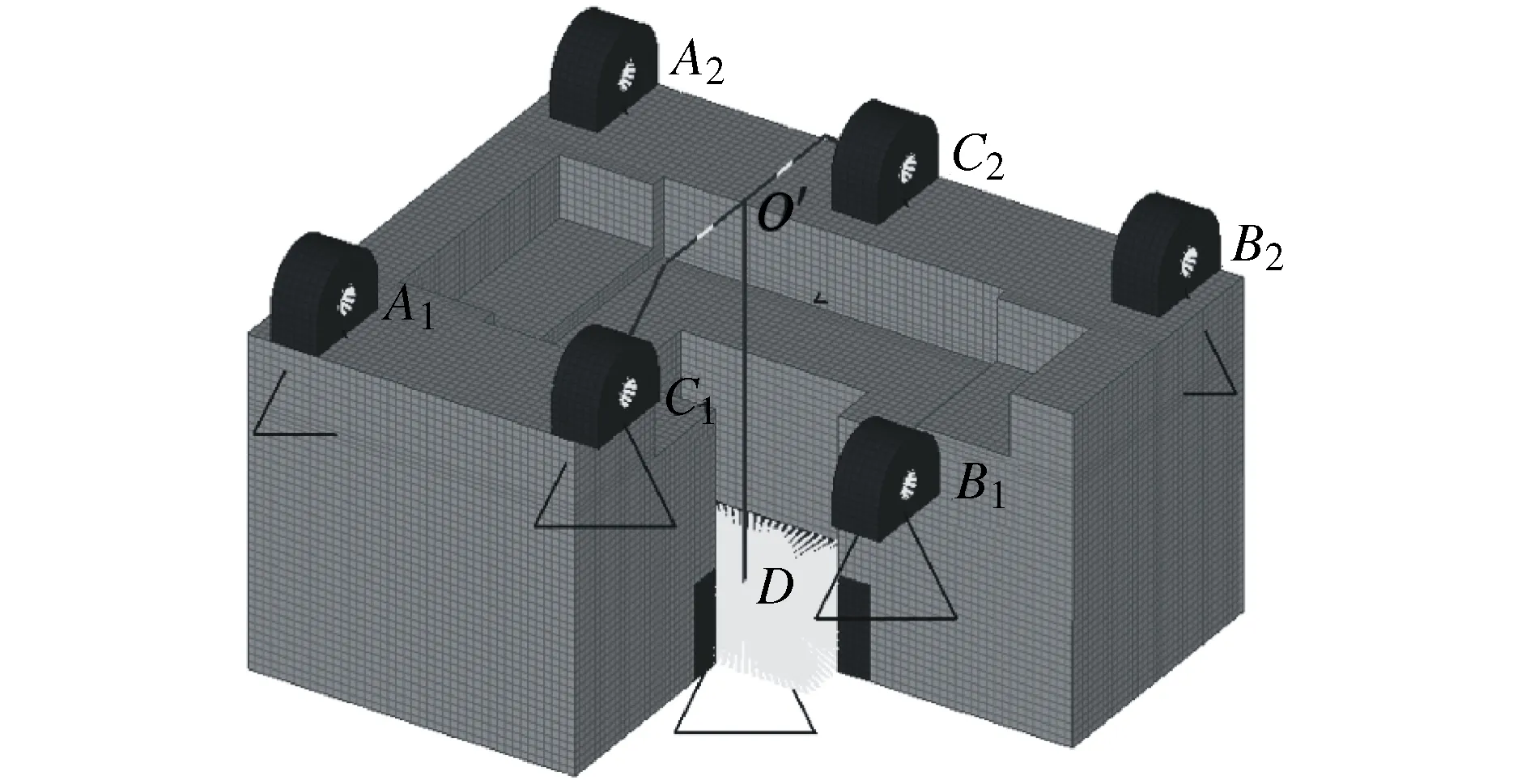
图4 柔性机构拓扑优化有限元模型(剖视)

如图4所示,原点位于吊钩的摆动中心,定支座的轴线方向为X轴,未发生变形时的摆臂轴线和动支座轴线分别为Z轴和Y轴。各联接点坐标分别为A1(-90,70,23)、A2(-90,-70,23)、B1(90,70,23)、B2(90,-70,23)、C1(0,70,23)、C2(0,-70,23)和接触点D(0,0,123)。

2) 材料定义

本文关注的是柔性机构的材料分布对其性能的影响,涉及的材料参数有弹性模量E和泊松比μ,对于动支座和摆臂,取E=210 000 MPa和μ=0.3。

柔性机构的材料为复合橡胶材料,各项参数随变形程度而改变,且呈非线性变化。考虑到现有复合橡胶材料的性能,取E=24 MPa、μ=0.45,密度取1 g/cm3。

3) 边界条件

本文通过添加等效作用力模拟吊装平台的倾斜状态,因此约束螺栓联接点A1,A2,B1和B2的3个方向的位移自由度,点C1和C2和动支座固定联接,动支座保留绕X轴转动自由度,吊钩与动支座通过铰链副联接。

根据起吊的发射箱质量为7吨及快速吊装的设计要求,取满足要求的直柄单钩毛坯质量为8.8 kg[20]。考虑到吊钩可能添加的导向结构,取吊钩等效质量为10 kg。根据质点到D点的距离,设作用在D点的等效重力大小为192.4 N。

发射箱质量较大,实际应用中的联接和材料均难以达到理想状态,因此负载工况下的偏角要求容易满足。为了降低负载状态下柔性机构的应力,延长其使用寿命,通过优化柔性机构的柔度降低其负载工况下的应力。本文通过添加强制位移使吊钩与重力方向重合模拟负载工况[21]。

为保证柔性机构的对称性,空载工况下设4个等效作用力方向不同的子工况及负载工况下D点的位移载荷如表1所示。

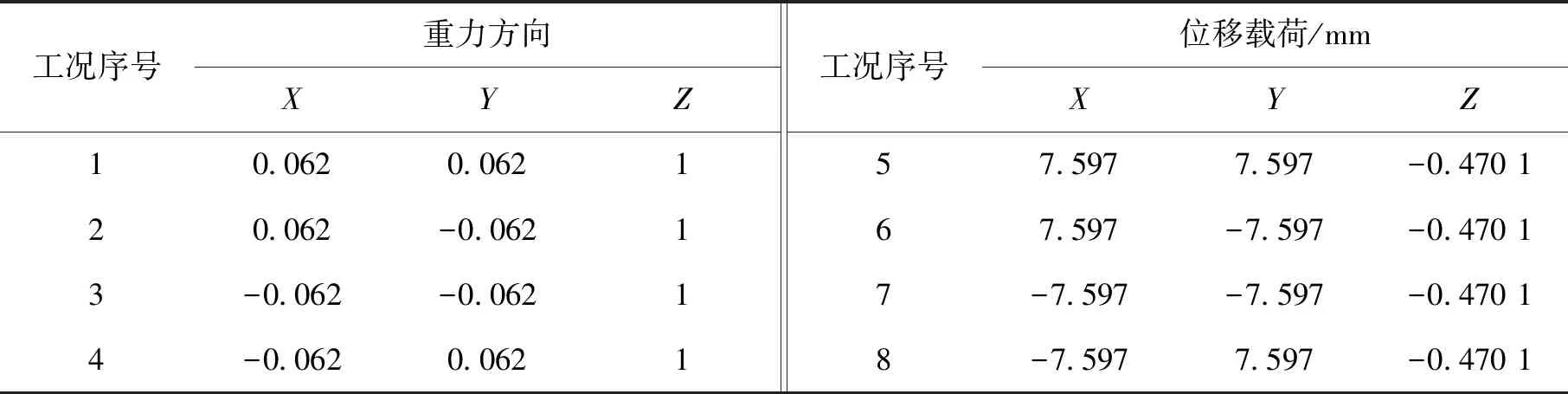
表1 部分边界条件

3.2 优化模型

柔性机构满足静态刚度和柔度的前提下,可以通过最大化结构的动态响应,提高结构的动态刚度,进而缩短柔性机构对准所需的时间。为了避免某一阶次的频率增大时其它阶次的频率降低带来的频率目标函数振荡现象,需要定义一个单独的固有频率优化目标函数,由式(2)得

(6)

式中：Λ(x)为平均频率;λk为第k阶特征频率;wk为第k阶频率的权重。

空载工况以力为载荷,其刚度最大问题等价于柔度最小问题,应变能越小则柔度越小。负载工况以位移为载荷,此时应变能越小则柔度越大。由折衷规划法得综合考虑空载刚度、负载柔度及动态振动频率的多目标拓扑优化模型为:

(7)

4 柔性机构拓扑优化实验

4.1 优化参数确定

1) 工况权值

根据柔性机构材料的性能可以调整空载工况和负载工况的权值以满足柔性机构的工作要求,如当材料弹性模量较小则增加空载工况的权重以更好的满足刚度要求。本文各工况的权重均取wi=0.125,各阶频率权重均取wk=0.25,为了突出柔度函数的重要性,取w=0.4。

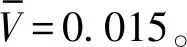
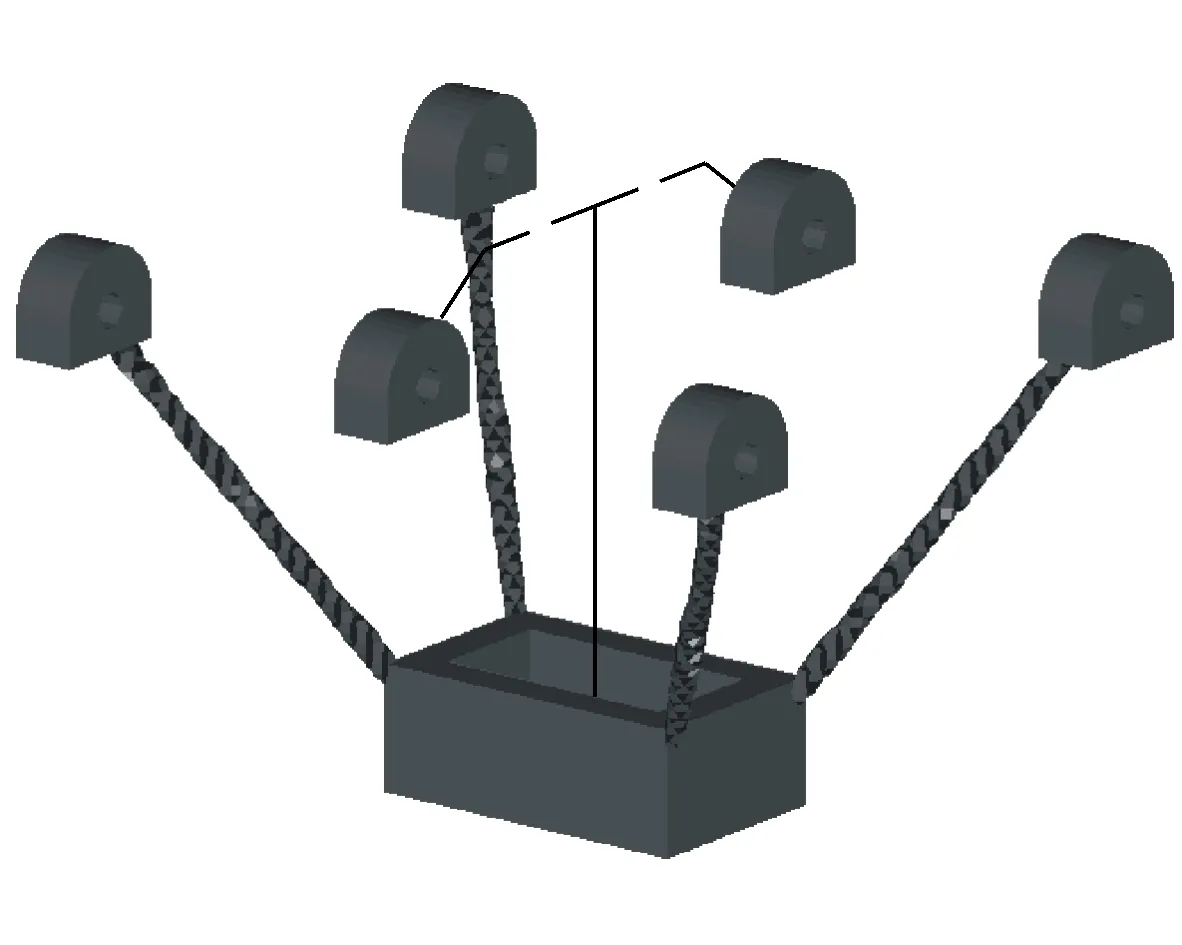
图5 空载工况单目标优化结果

3) 优化函数极值

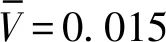
4.2 优化结果

选择OptiStruct默认收敛容差(0.5%)为收敛准则,经过60步迭代,保留密度阈值0.51以上的单元,柔性机构拓扑优化结果如图6所示。可以看到,优化结果保留了较多的弧形结构和腔体,符合工程中允许产生大变形的机械结构(如蜂窝结构)的结构特点。综合考虑实际加工工艺和柔性机构联接等因素,对拓扑优化结果抽象出最终的柔性机构几何模型如图7所示。

图6 柔性机构多目标拓扑优化结果

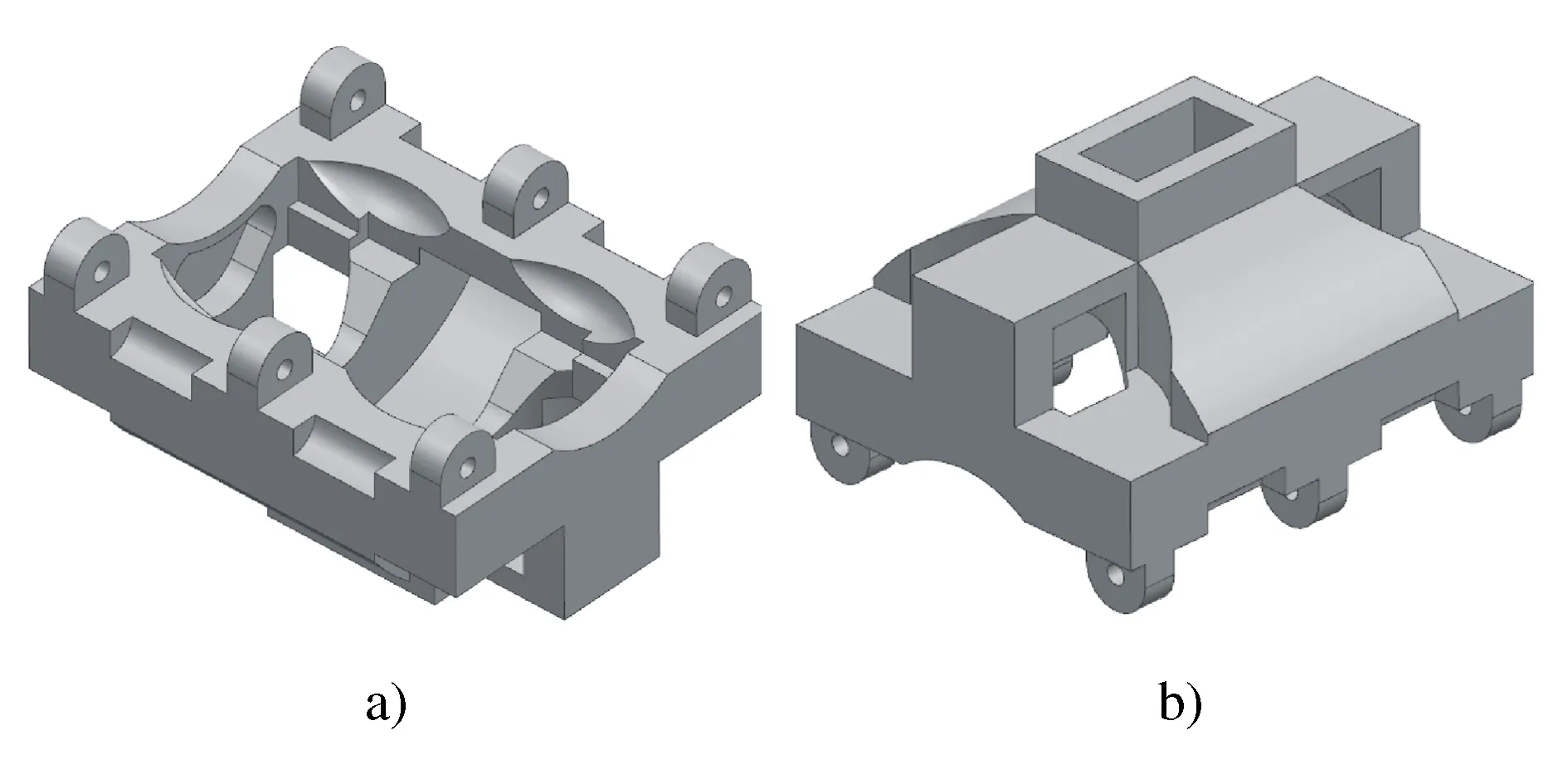
图7 柔性机构几何模型

图8为柔度迭代历程,从图8中可以看出,空载工况下的柔度有了适当的提升同时负载工况下的柔度有相应降低。既柔性机构空载工况下的整体结构刚度降低以提升负载下的整体结构柔度,并达到综合性能最优的状态。

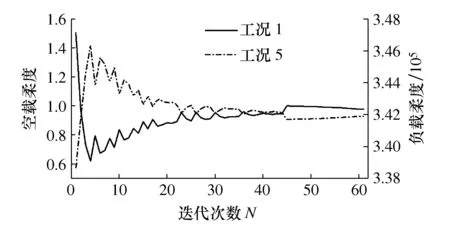
图8 柔度迭代历程

图9为频率迭代历程,可以看出前4阶频率在一定程度上都得到了提高且没有发生频率振荡现象。另一方面,58步～60步的函数值依次为:0.077 50、0.076 90、0.076 75,柔度和频率的变化趋于平缓,保证了迭代过程的收敛性。

图9 频率迭代历程

4.3 模型检验

在Abaqus中对优化后并重新设计的柔性机构进行仿真分析。为了更加贴近柔性机构的真实情况,仿真模型保留了柔性机构间的接触并通过螺栓联接约束二者的相互滑动,其它设置与拓扑优化模型相同。仿真分析结果如图10所示。

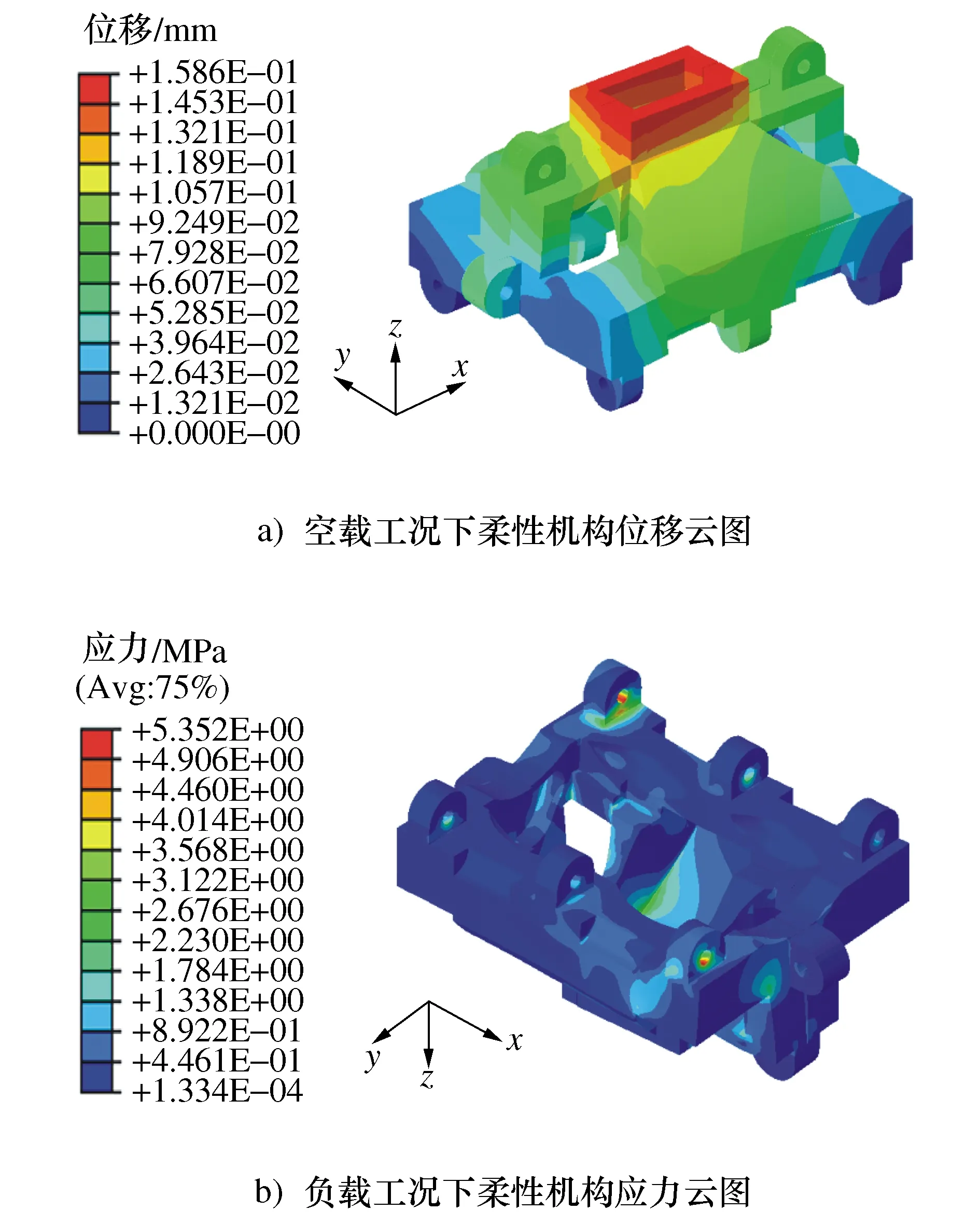
图10 Abaqus检验结果

从图10a)中可以看出优化后的柔性机构空载工况下的最大位移出现在柔性机构与吊钩的接触部分,位移最大值为0.15 mm等价于0.07°的角位移,满足空载工况下的刚度要求。如图10b),负载工况下柔性机构最大Mises应力出现在位移方向的螺栓联接凸台,应力值为5.3 MPa,同时柔性机构整体的应力较小且分布均匀,满足负载工况下的柔度要求。

5 结论

采用以SIMP方法为拓扑优化方法的OptiStruct软件对柔性机构进行拓扑优化实验。以应变能表示力载荷作用下的刚度和位移载荷作用下的柔度。采用折衷规划法定义空载刚度、负载柔度和低阶振动频率的多目标函数,消除了目标间的差异同时获得了各个优化目标的有效解。在优化过程中,各个子目标的收敛性较好,结果显示优化后的柔性机构满足空载刚度要求且负载柔度得到了优化,同时柔性机构的低阶频率也得到了提高。