柴油甲醇双燃料发动机进气均匀性优化

2022-06-27贾德文徐加恒雷基林邓晰文邓伟

机械科学与技术 2022年6期

贾德文，徐加恒，雷基林，邓晰文，邓伟

(昆明理工大学云南省内燃机重点实验室,昆明 650500)

随着排放法规日益严苛和石油资源的日渐减少,煤炭和天然气将成为能源结构调整的方向,因此需要寻找合适的发动机替代燃料[1]。由于甲醇在理化性质上具有辛烷值高、含氧量丰富、碳含量低等特点,被认为是一种理想的发动机替代燃料。在柴油机上,由于甲醇与柴油不互溶,而且难以压燃,所以甲醇在进气管内喷射形成均质混合气,然后在缸内依靠柴油引燃,是甲醇在柴油机上应用的主要方式[2]。甲醇在进气总管喷射时,柴油机进气总管通常为单侧进气方式,另外随气门开启和关闭产生进气压力波动,造成各缸甲醇混合气进入量存在差异,会直接造成各缸间进气均匀性以及工作性能的差异[3-4]。许多学者进行了汽油机和柴油发动机进气均匀性的相关工作,其主要采用数值模拟的方法针对影响进气不均匀度的进气歧管角度[5]、稳压腔容积[6]、进气管结构[7-8]、进气歧管温度[9]、点火顺序[10]等关键参数进行了大量的研究,但针对的是单一结构参数对进气均匀性的影响,故无法考虑各个参数间的相互作用。因此,对发动机的进气系统结构参数综合考虑进行优化分析,具有重要的意义。

改变进气系统中的结构参数如直径、长度和谐振腔容积以及进气正时,可以有效利用进气谐振效应,提高充气效率,降低各缸甲醇混合气进入量差异,从而提高发动机整体进气均匀性和性能。本文以某四缸柴油甲醇双燃料发动机为研究对象,分析进气系统中的进气总管、进气歧管、进气正时等结构参数对进气不均匀度的影响,在此基础上,建立响应面模型并利用多岛遗传算法对进气不均匀度进行优化,提高了发动机的进气均匀性。

1 研究对象和方法

1.1 研究对象

研究对象为某直列四缸、增压中冷、电控单体泵柴油甲醇双燃料发动机,其主要技术参数详见表1。

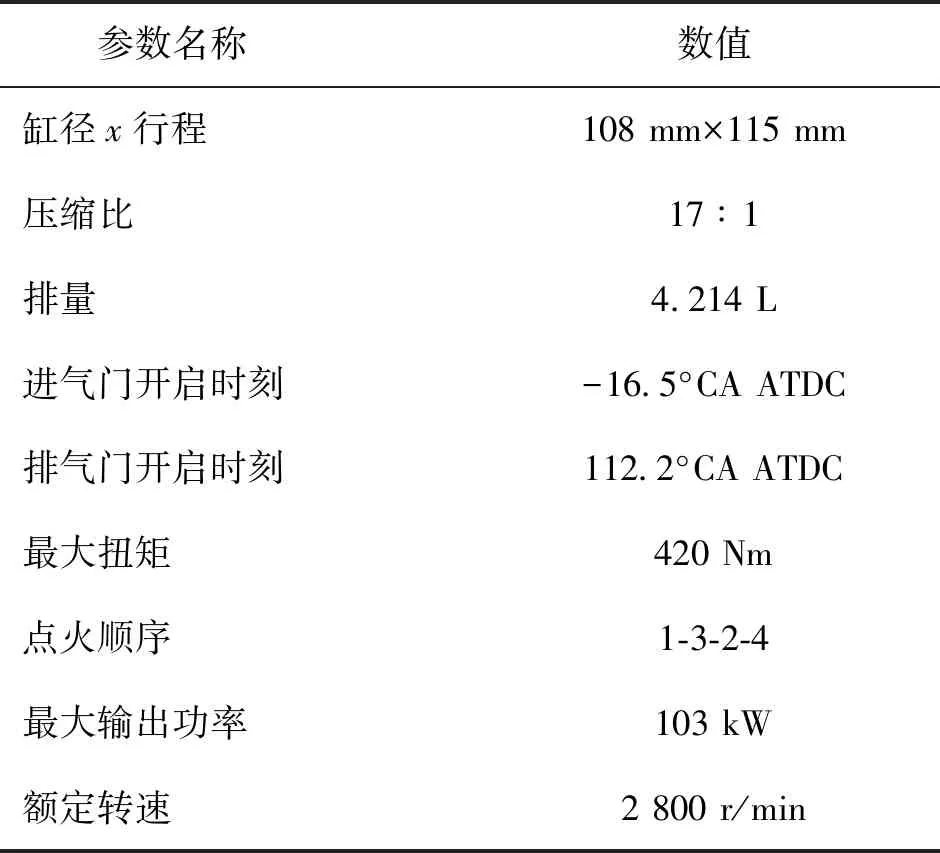
表1 发动机主要技术参数

柴油甲醇双燃料发动机的进气管结构为进气总管单侧进气方式如图1所示,其主要技术参数详见表2。

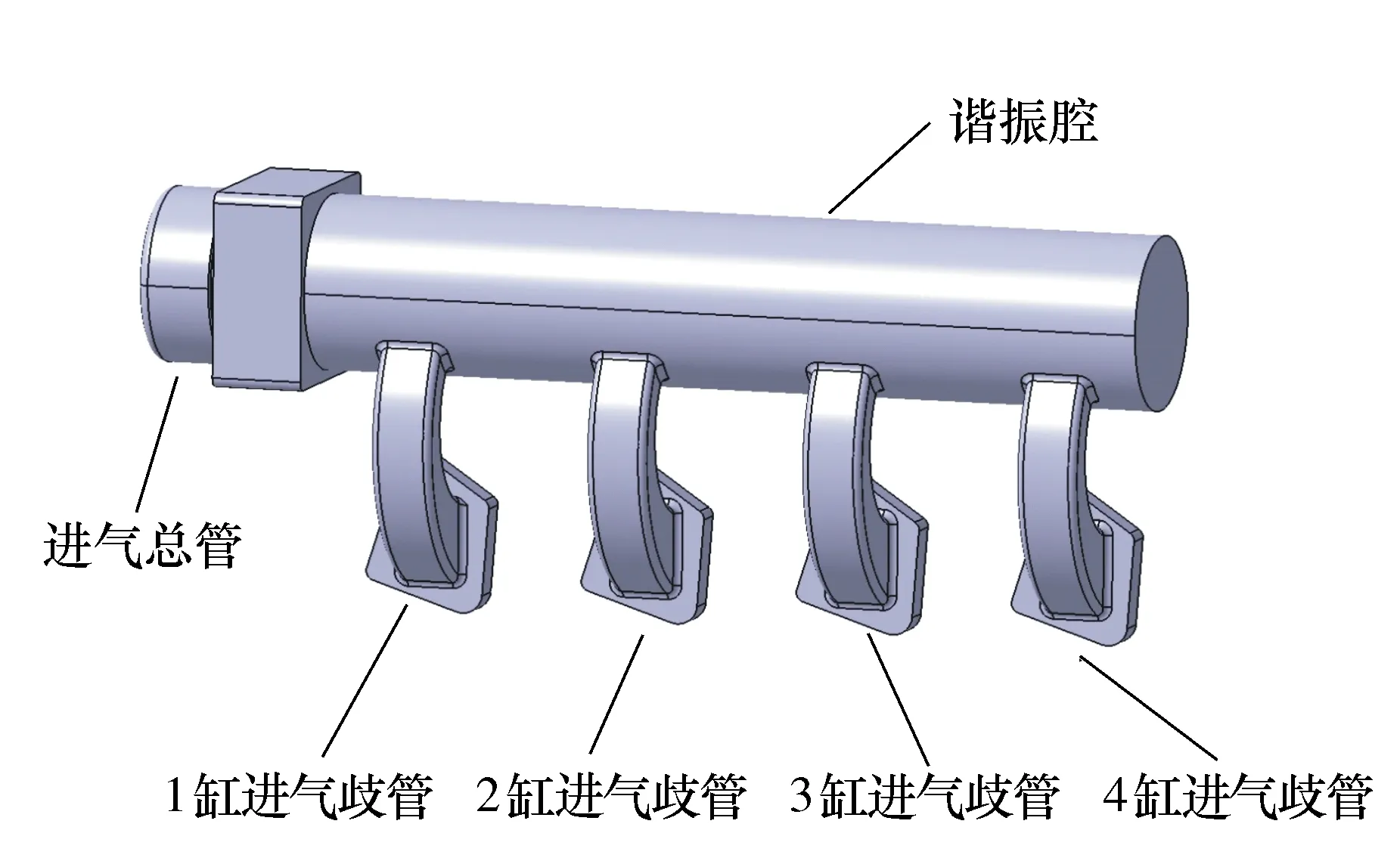
图1 进气总管单侧进气方式的进气系统示意图

表2 进气系统主要技术参数

1.2 研究方法

一维流动计算时需要满足流动模型的基本方程[11]为：

质量守恒方程

(1)

动量守恒方程

(2)

能量守恒方程

(3)

式中:ρ为气体密度,kg/m3;u为气体流速,m/s;M为管道当量直径,mm;L为管道截面积,mm2;p为压力,Pa;f为摩擦因数;q为外界传入微元体中的热量传热率。

一维仿真软件GT-power是以管内一维流动和缸内容积法为理论基础,各离散单元通过相连的边界进行质量、动量及能量的传递和交换。根据上述的理论和发动机结构参数建立了柴油甲醇双燃料发动机的仿真模型如图2所示。主要包括:进排气系统、喷醇器、喷油器、气缸、增压器、曲轴箱等。

图2 柴油甲醇双燃料发动机GT-Power模型

1.3 研究方案

选取负荷75%、转速1 660 r/min、甲醇替代率为0、30%两种工况进行模型验证,其中甲醇的替代率是通过燃料的质量分数和燃烧热值来进行计算的,即

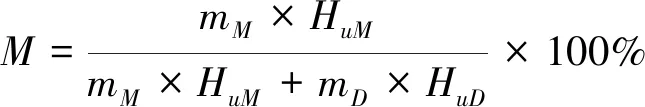
(4)

式中:mD为双燃料模式下单位时间内柴油的消耗量,kg/h;mM为双燃料模式下单位时间内甲醇的消耗量,kg/h;HuD为柴油的质量低热值,取HuD=42.5 MJ/kg;HuM为甲醇的质量低热值,取HuM=19.66 MJ/kg;当M=0时,表示纯柴油模式。

为验证计算模型的准确性,通过仿真计算对比文献[12]中的试验数据,图3和图4分别为甲醇替代率为0、30%仿真计算结果和试验结果的对比。由图3和图4可见,该仿真模型计算得到的缸内压力与文献试验结果的最大误差分别为2.1%、3.6%。由此可知,该仿真模型是合理的,能够用于该款柴油甲醇双燃料发动机后续的改进和优化。

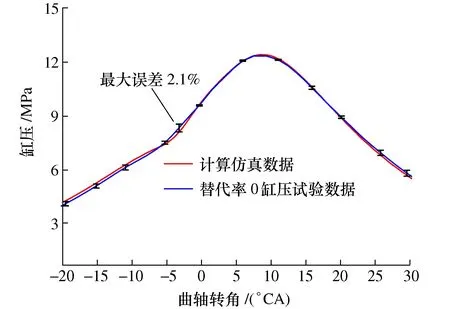
图3 替代率0，166 0 r/min时的缸内压力对比

图4 替代率30%，1 660 r/min时的缸内压力对比

2 进气不均匀度的定义

由于发动机在工作过程中各缸的进气量不相同,为了定量地表达发动机的进气不均匀程度,定义进气流量不均匀度为T如式(5)所示,T的值越小代表越均匀。

(5)

式中:Fmax为气缸中进气量最大的气缸的进气质量流量,g/s;Fmin为气缸中进气量最小的气缸的进气质量流量,g/s;Fmean为各缸进气质量流量的平均值,g/s。

3 进气均匀性优化

研究不同进气结构参数对甲醇柴油双燃料发动机进气均匀性的影响,一般采用参变量扫值法,故无法考虑各个参数变量间的相互作用,所以优化结果容易受主观影响[13]。而响应面法的优点是可以找出整个参数的取值范围、研究参数变量之间相互作用关系、对优化目标建立响应面模型以及进行分析,进而寻求最优的参数,达到优化该目标的目的[14-16]。

3.1 设计变量及其取值范围的确定

在负荷75%、替代率为30%、转速1 660 r/min工况下对原机型进行仿真计算得到各歧管的进气质量流量如表3所示,通过式(5)计算得到原机型的进气不均匀度为10.35%。1缸和4缸歧管进气量和甲醇的流入量较大,使得各缸进气量和燃烧均匀性变差,这对整机的动力性能和排放等会造成不良影响。为使发动机各缸之间的进气和燃烧均匀性趋近相同,有必要对发动机歧管进行优化。根据流动力学原理,同时增大2、3缸进气歧管直径进行优化,并保持1、4缸进气歧管不变。

表3 发动机各歧管进气质量流量

由于进气系统结构参数较多,而且不是所有参数都是进气均匀性的关键影响因素,因此主要考虑以下因素:进气总管直径D1、进气歧管长度L、2、3缸进气歧管直径D2以及进气正时K共4个变量。对各个结构参数的研究方法主要是采用控制变量法,在保证其他参数不变的前提下,选定该参数的各个水平作为计算测试点,分析仿真计算后的进气不均匀度的变化规律。

以D2对进气不均匀度影响及其范围的确定为例,其他参数同理可得。D2从40 mm开始,依次增加2 mm,直至60 mm共11个水平进行计算仿真试验。由仿真计算获得所得的进气不均匀度和各歧管平均进气量如图5所示。

图5 2、3缸歧管直径对进气不均匀度与各歧管平均进气量的影响

由图5可知,在改变歧管直径40～50 mm过程中,进气不均匀度T由10.09%减少到3.59%,继续增大D2对于进气不均匀度的影响较小;各歧管平均进气量随D2增加而变大,在改变歧管直径44 mm～60 mm过程中,进气量由157 g/s增加到168 g/s。由此可以看出D2对发动机进气均匀性以及各歧管平均进气量影响较大,因此D2在48 mm时,可以保证进气量的同时降低进气不均匀度。其他3个参数同理可得,根据单一变量对目标的影响,确定参数范围可以提高响应面拟合的精度。单一变量仿真计算得到参数的范围与水平数设置如表4。

表4 各参数水平的设置

3.2 试验设计及方差分析

通过合理的试验方法选取样本点,可以有效建立各参数与响应之间的曲面模型,试验设计方法的运用可以快速识别关键试验参数,确定参数的最佳组合,并分析输入参数与响应之间的关系,以及用于构建回归方程和响应面模型等。本文采用Box-Behnken Design设计,通过较少的试验次数,取得的样本点分布具有更好的均匀性,使得各参数与响应之间的拟合精度更高。选取D1(A)、L(B)、D2(C)以及K(D)为优化变量设计四参数三水平响应面仿真(表4)。试验结果通过正交试验软件回归分析得到二次回归方程T(x),将进气不均匀度二次回归方程经过二次拟合后,得出进气不均匀度回归方程方差分析结果(见表5)。

由表5可知,该模型的显著性水平P<0.0001,说明所选模型显著程度高。比较F值得出,各参数对进气不均匀度的影响强弱顺序为:B>D>C>A,表明模型选择合适。从模拟项的P值与0.05比较大小可知,模拟一次项B、C、D与模拟二次项AD、BC、BD、A2、B2、C2均显著,与方差分析结果一致。

表5 响应面模型的方差分析

3.3 响应面模型的建立

由试验设计到一组仿真模型信息的数据点,利用回归分析方法可以建立起所需的响应面模型。由Box-Behnken Design设计得到样本点,并采用函数多项式作为基函数通过最小二乘回归来构造近似函数建立关于以进气不均匀度为响应值的各参数交互作用响应面,以D1、L、D2、K这4个参数为设计变量,进气不均匀度T为优化目标,可以建立6个响应面的3D曲面。选取其中两个具有代表性的3D曲面,如图6和图7所示。由图6和图7可知,以D1、L、D2为设计变量,T为响应值的模型中存在进气不均匀度最小稳定点。

图6 进气总管直径与进气歧管长度的交互作用响应面图

图7 进气歧管长度与2、3缸进气歧管直径的交互作用响应面图

3.4 响应面模型的精度分析

为了保证响应面模型拟合进气结构参数与进气不均匀度函数关系的有效性,必须进行检验。检验响应面有效性的方法是首先在设计变量空间内随机生成几个样本点,并调用仿真模型进行计算;其次计算在样本点处响应面上对应值与计算值的偏离程度。随机选取的12个随机样本点如表6所示。

表6 随机生成的样本点

响应面模型的精度是通过复相关系数来进行评定,计算公式为

(6)

根据公式计算得到的R2=0.971,表明建立的响应面模型符合精度要求,由函数多项式法建立的响应面可以用于替代仿真模型进行下一步的优化。

3.5 最优进气不均匀度确定

在响应面拟合精度较好的基础上,结合优化算法可以在较少的计算时间完成对进气不均匀度的优化。遗传算法是具有鲁棒性的搜索算法,可以解决复杂的大尺度、多变量非线性反演问题,多岛遗传算法是在遗传算法基础上改进的,具有比普通遗传算法更好的计算效率及全局优化的能力[17-18]。选取负荷75%、替代率为30%、转速1 660 r/min工况下的最小进气不均匀度为优化目标如式(7)所示,以参数的取值范围作为优化目标的约束条件如式(8)所示,并采用多岛遗传算法进行参数优化。

目标函数为

Tm=min[T(D1,L,D2,K)]

(7)

约束函数为

(8)

多岛遗传算法中为了得到较稳定的结果,采用两点交叉方式进行杂交,最优淘汰制进行选择,统一变异方式进行突变,设置初始种群个体为10,岛数为4,进化代数为10,交叉概率为0.8,共对400个数据点进行寻优,进气不均匀度目标函数迭代寻优过程如图8所示。