飞机IDG可靠性参数估计方法对比研究

孔祥芬,刘敬赟,王杰,唐淑珍

(中国民航大学 航空工程学院,天津 300300)

2020年初新冠肺炎疫情的突然爆发,对全球航空运输业造成了极大的负面影响,与航空运输业密切相关的航空维修业也受到了前所未有的冲击和挑战[1]。为落实我国对当前民航 “保安全运行、保应急运输、保风险可控、保精细施策”的要求以及为后续航空市场的恢复做准备,不少维修单位开始调整对整机和航空附部件的维修计划。其中准确获取航空附部件的可靠性参数对调整维修计划起关键性作用。整体驱动发电机(IDG)作为飞机电源系统的核心部件[2-3],为机载用电设备提供恒频交流电,其可靠运行是飞机安全运行的重要保障。因此,结合飞机IDG的故障数据特点,寻找可更加客观准确估计飞机IDG可靠性参数的方法,对提高飞机IDG的使用可靠性和制定经济合理的维修计划具有重要意义。

针对飞机IDG这类关键航空附部件产品,可靠性要求高而能获取的历史故障数据较少,属于小样本范畴(n≤30)[4]。目前工程实际中普遍采用最小二乘法(Least square regression,LSR) 对具有小样本故障数据特征的部件进行可靠性分析。文献[5]对竞争失效可靠度模型中的参数采用最小二乘法进行估计。文献[6]通过对比分析中位秩公式和平均秩次法的拟合效果,运用最小二乘法对航空装备进行参数估计分析;随着现代应用统计学和计算机科学的发展,出现了不少针对小样本数据进行可靠分析的方法,文献[7]针对某机械产品的故障数据小样本删失的特点,建立了分布识别和参数估计模型利用支持向量机训练样本进而对数据进行预测扩充,最后利用扩充后的样本进行可靠性参数估计;文献[8]使用支持向量回归模型对小样本故障数据进行威布尔分布MTBF估计;文献[9]将支持向量回归应用到风电机组的可靠性参数估计中,并提出该方法更适用于小样本数据的情况;文献[10]提出一种支持向量机的改进算法——最小二乘支持向量机对服从威布尔分布的发动机系统进行参数估计;文献[11]通过模拟仿真得到滚动轴承的数据,采用最小二乘支持向量机进行回归预测其剩余使用寿命。

目前在航空维修可靠性分析方面,较少考虑到部件的故障数据为小样本时对可靠性参数估计的影响。因此,以某航空公司B737-800飞机IDG部件的故障数据(可靠性指标故障间隔时间)为研究对象,以威布尔分布为例,对比分析最小二乘支持向量回归机、支持向量回归机和最小二乘法3种方法的可靠性参数估计结果,找到更加客观准确的飞机IDG可靠性参数估计方法。

1 飞机IDG的可靠性参数估计

1.1 飞机IDG可靠性分布模型

威布尔分布可以描述产品部件处于浴盆曲线各个阶段的分布规律的特征,比其他的分布模型的适用范围更广,尤其适用于机电类产品失效的分布规律描述。研究和实践结果表明,飞机机电、液压等系统及其子系统、零部件大都适用威布尔分布来拟合[3,12-14]。

两参数威布尔分布的累计失效概率函数为

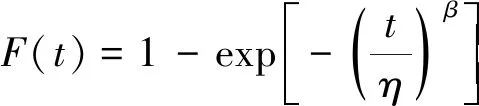
(1)

式中:t为部件产品的故障时间;β为形状参数；η为尺寸参数。

一般地,当样本量n≤20时通常使用中位秩公式来求解累计失效概率密度

(2)

式中:n为部件故障数据的样本量；i为部件故障时间从小到大排序序号。

将威布尔分布模型线性化为

ln(ln[1/(1-F(t))])=βln(t)-βln(η) (3)

设:

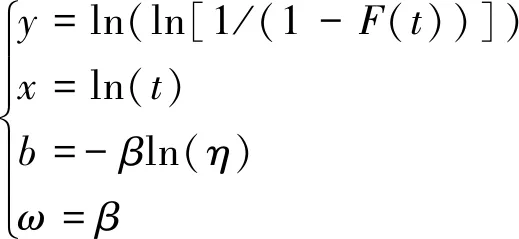
(4)

可得线性关系式为

y=ωx+b

(5)

对于一组故障数据样本{ti},i=1,…，n,将数据线性化后得到数据集T={(x1,y1),(x2,y2),…(xn,yn)}。数据集T={(x1,y1),(x2,y2),…，(xn,yn)}线性相关程度通常用相关系数ρxy来度量，即

(6)

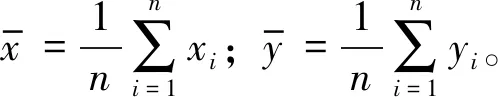
1.2 最小二乘法

最小二乘法LSR通过最小化观测值和拟合值之间误差的平方和,来寻找数据的最佳函数匹配,该方法对观测样本量无特定要求[15]。当研究对象服从威布尔分布时,参数估计思路如下:

对于平面直线l:y=ωx+b与数据集T={(x1,y1),(x2,y2),…(xn,yn)},量|yi-(b+ωxi)|描述了点(xi,yi)沿y轴方向到直线l的距离。令

(7)

描述数据集T={(x1,y1),(x2,y2),…，(xn,yn)}与直线l的偏离程度。显然,偏离越小越好。

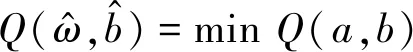
(8)

(9)

解该方程组得:

(10)

由式(4)得β和η的估计值为:

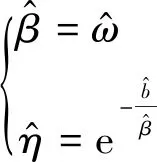
(11)

1.3 支持向量回归机

支持向量回归机(Support vector regression,SVR)是通过一个非线性函数变换,将低维空间映射到高维空间,在高维空间找到线性可分的超平面,使得拟合点到超平面中最远的样本点的“距离”最小。该算法在解决小样本问题中表现出了独特的优势[16]。

对于给定的数据集

T={(xi,yi)，…，(xl,yl)}∈(Rn×y)l

(12)

式中:xi∈Rn；yi∈y=R；i=1,…,l。

在高维空间中,输入样本点和输出样本点回归函数关系表示为

f(x)=ωTφ(x)+bφ:Rn→F

(13)

式中:ω为权向量；b为偏差量;φ(x)为高维空间F中非线性变换函数。

选择适当的数ε>0和惩罚参数C>0,支持向量回归机模型可表示为求解以下优化问题:

(14)

(15)

一般引入Lagrange函数求解此类问题,

(16)

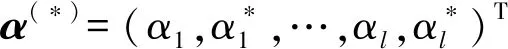
进而得到优化问题的对偶形式

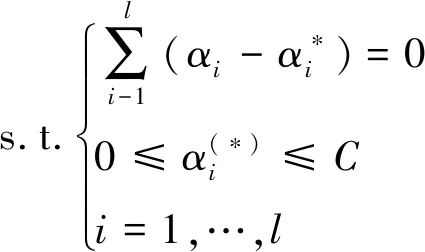
(17)

解得

(18)

解得线性方程

(19)

式中k(xi,xj)为满足Mercer条件的核函数。

1.4 最小二乘支持向量回归机

最小二乘支持向量回归机(Least squares support vector regression,LSSVR)是在SVR的基础上发展而来。与SVR不同的是,LSSVR在优化问题用平方误差项代替了SVR中的ε-不敏感损失函数,降低了模型优化过程中的复杂性,克服了模型训练时间较长的问题[17]。

对于给定的数据集

LSSVR可表示为求解以下优化问题:

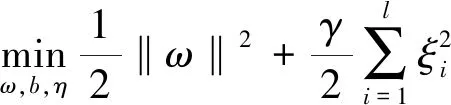
(20)

s.t.y-((ω·φ(x)+b)=ξii=1,…,l

式中:γ为正则化常数；ξi为误差项。

一般用拉格朗日法求解这类优化问题:

(21)

式中αi是拉格朗日乘子。

(22)

引入核函数K(xi,xj)=φ(xi)·φ(xj)。根据式(22),优化问题转化为求解线性方程:

(23)

最后可得回归方程为

(24)

1.5 SVR和LSSVR方法下的Weibull分布参数估计

步骤1 核函数及其参数的选择。SVR和LSSVR模型性能的优劣主要取决于所选择的核函数及其参数。其中主要的核函数有线性核函数,多项式核函数、RBF核函数、sigmoid核函数。本文采用常用的RBF核函数。

K(xi,xj)=exp(-‖xi-xj‖/σ2),γ>0

(25)

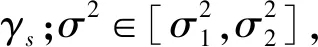
(26)

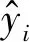
步骤2 Weibull分布参数估计。分别使用MATLAB的LIBSVM、LS-SVM工具箱,对SVR和LSSVR模型进行参数寻优,得到最优回归直线。然后,结合图估计法对飞机IDG所服从的威布尔分布进参数估计:根据式(4)和式(5)可知,形状参数β为所得最优回归直线的斜率;尺寸参数η又称特征寿命,即当累计故障概率分布函数F(t)=63.2%时所对应的寿命。根据式(4),当F(t)=63.2%时相应的yi=0,故直线yi=0与所得回归直线交点的横坐标即为lnη的值。

1.6 参数估计结果评价

通常,可采用统计学中的统一化的均方根误差(NRMSE)对不同参数估计方法所得结果进行定量评价。

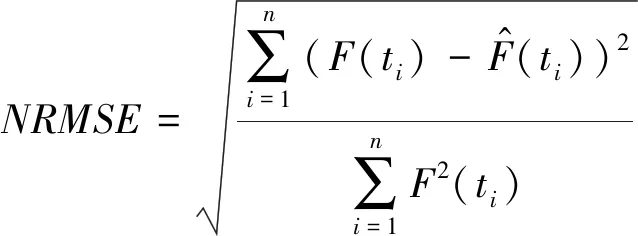
(27)

2 案例分析

2.1 飞机IDG部件介绍

飞机整体驱动发电机(IDG)又称组合驱动发动机,是目前国内外一些大中型客机供电系统中普遍采用的主要电源,如B737系列,A320等。以B737-800机型作为研究对象,其中每架B737-800飞机配备两台飞机IDG,分别位于左、右发动机附件轮箱上。飞机IDG主要由恒速传动装置(Constant speed drive,CSD)和交流发电机两大部分组成,主要工作原理为:恒速传动装置将变化的发动机转速转变为恒定的转速,然后通过交流发电机产生115 V/400 Hz的恒频交流电,以保障机载用电设备的正常运行。飞机IDG的工作原理如图1所示。

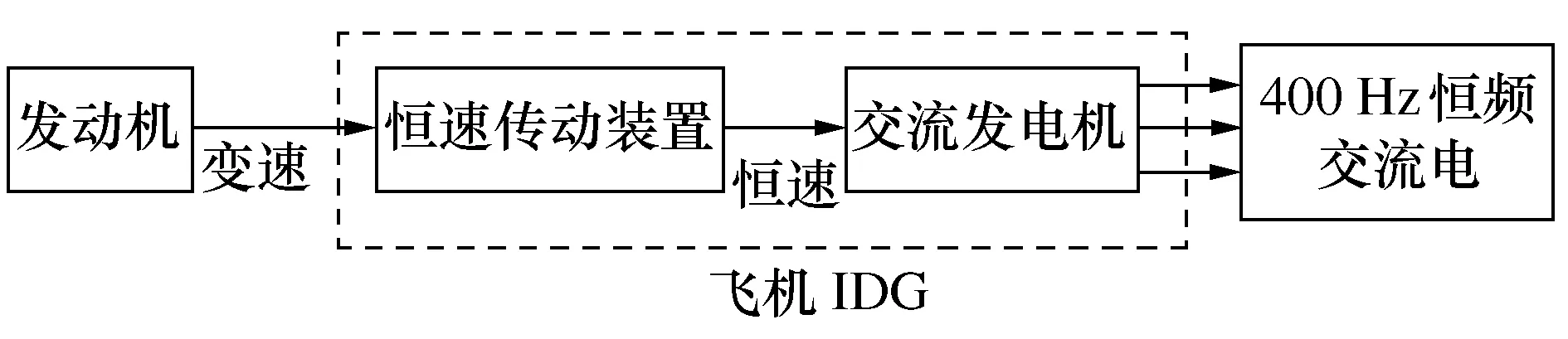
图1 飞机IDG的工作原理

2.2 故障数据预处理

本文统计的故障数据来源于国内某航空公司45架B737-800飞机电源系统的故障数据电子记录,记录时间为2015年2月到2018年7月。通过对该组故障数据记录归类、筛选预处理,从中提取出飞机IDG部件的故障发生时间、故障描述、维修措施和飞行时间等故障数据信息。最终得到飞机IDG部件的故障数据即同一机号同一位置的IDG部件相邻两次故障间的飞行时间(可靠性指标故障间隔时间),共计15条,部分飞机IDG故障数据记录如表1所示。

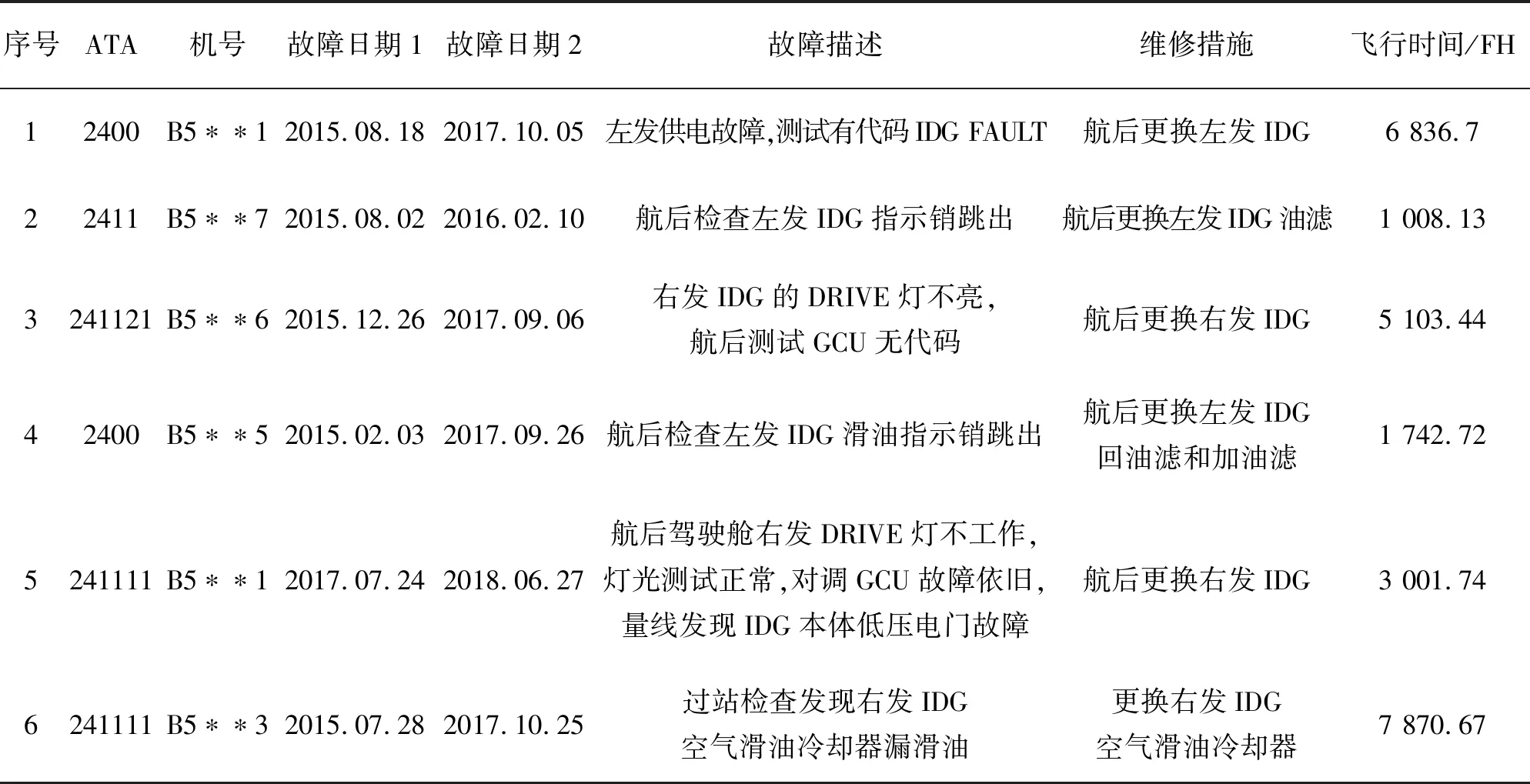
表1 飞机IDG的部分故障数据记录

然后,将飞机IDG故障数据进行从小到大排序,如表2第1列所示。

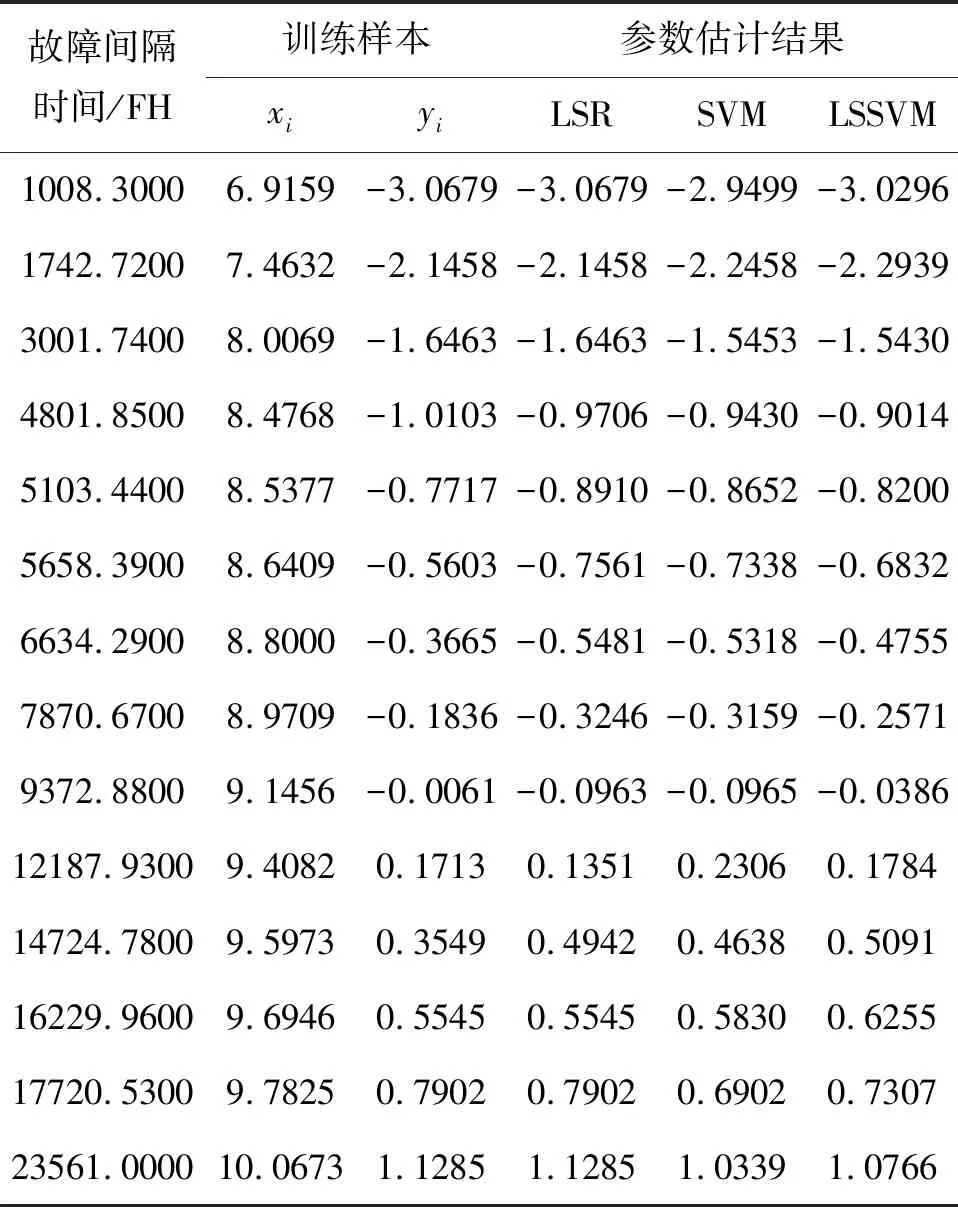
表2 故障数据、训练样本及参数估计结果

采用式(3)将得到的飞机IDG故障数据线性化处理,得到数据集T={(x1,y1),(x2,y2),…(xn,yn)}。计算x与y之间的相关系数得

(28)

根据结果可知,x与y近似线性关系,说明该B737-800机队飞机IDG的寿命分布较好地服从二参数威布尔分布。

2.3 飞机IDG可靠性参数估计

在MATLAB平台上分别对SVR和LSSVR进行编程。SVR和LSSVR采用网格搜索法和交叉验证法对参数进行优化选择。同时得到最优回归拟合线,分别如图2和图3所示,拟合结果如表2第5和第6列所示。

图2 SVR方法下的最优拟合直线

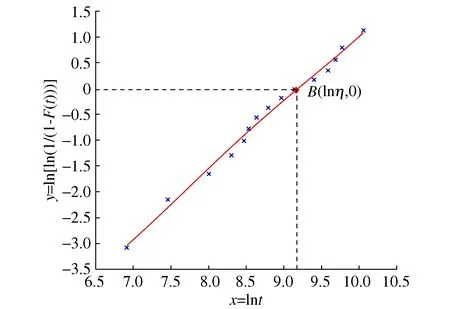
图3 LSSVR方法下的最优拟合直线

根据图估计法,SVR和LSSVR所得拟合直线的斜率即为形状参数β,通过图2和图3中的虚线所示,直线y=0与直线的交点A的横坐标x=lnη,从而得到尺寸参数η的值。同时,运用LSR得到参数估计结果,3种方法的结果如表3所示。

表3 飞机IDG的可靠性参数估计结果

2.4 不同参数估计方法的结果对比研究

为了评价3种方法的可靠性参数估计效果,采用式(22)指标进行可靠性参数估计结果评价,所得结果如表4第2列所示。

表4 飞机IDG(实际数据)的可靠性参数估计结果评价

从以上分析结果可知,LSSVR的误差最小,参数估计精度最高;SVR其次;LSR的误差最大,参数估计精度最低。

其次,3种可靠性参数估计方法在MATLAB平台的运行时间如表4第3列所示。由于LSR无需进行模型内的参数寻优,速度最快。LSSVR相比SVR运行速度较快。

2.5 不同样本量下的3种参数估计方法对比研究

在飞机IDG故障数据为小样本情况下,为观察样本量变化时3种可靠性参数估计方法的稳定性[18]。将采集到的2015年～2018年飞机IDG故障数据,分成一年内的故障数据(即2015年～2016年)、两年内的故障数据(即2015年～2017年)和三年内(即2015年～2018)的故障数据,对各组的故障数据分别使用LSR,SVR,LSSVR这3种方法估计飞机IDG可靠性参数,并以NRMSE为指标进行参数估计结果评价,评价结果如图4所示。

图4 不同样本量下3种方法的参数估计误差结果(实际数据)

由图4可知,随着样本量的减小,3种可靠性参数估计方法的误差均呈现出增大的趋势。但LSSVR的参数估计误差增长速度最慢,受样本量变化的影响最小,具有较高的稳定性。当样本量相同时,LSSVR的参数估计误差普遍小于SVR和LSR。即在飞机IDG故障数据为小样本情况下,相比LSR和SVR,LSSVR所得参数估计结果普遍具有较高的精度。

3 蒙特卡罗仿真验证

为进一步验证3种可靠性参数估计方法对比分析结果的准确性,对服从两参数威布尔分布的飞机IDG部件进行蒙特卡罗仿真[19],其中形状参数和尺度参数分别设定为β=1.5,η=10 000。

首先,对3种方法的可靠性参数估计结果及其评价进行验证。将飞机IDG部件的运行时间设定为20 000FH进行多次仿真,得到小样本故障数据{ti}。将该组故障数据{ti}线性化后得到小样本数据集T={(x1,y1),(x2,y2),…,(xn,yn)}后,采用3种方法进行可靠性参数估计。3种方法下的可靠性参数估计结果及其评价如表5所示。

表5 飞机IDG(仿真数据)的可靠性参数估计结果及其评价

然后,对样本量变化时3种方法的可靠性参数估计结果的稳定性进行验证。将故障样本量分别设定为5、10、15、20进行蒙特卡罗仿真。根据多次仿真抽样得到故障数据样本,采用3种参数估计方法计算得到不同样本量下3种方法的可靠性参数估计评价结果,如图5所示。

图5 不同样本量下3种方法的参数估计误差结果(仿真数据)

由两组仿真结果可知,当飞机IDG故障数据为小样本时,LSSVR算法下的可靠性参数估计误差最小,SVM次之,LSR较大,与案例分析中所得结果一致;3种可靠性参数估计方法在MTALAB平台的运行时间、当样本量变化时的稳定性所得结果也与案例分析中所得结果基本一致。

4 结论

本文针对飞机IDG可靠性高而故障数据为小样本的特点,分别采用LSSVR、SVR和LSR对飞机IDG进行可靠性参数估计。通过实际案例分析以及蒙特卡罗仿真验证,对比分析了3种方法的可靠性参数估计结果。可得以下结论:

在飞机IDG 可靠性参数估计中,当获取的故障数据属于小样本(n≤30)、寿命分布服从两参数威布尔分布时,LSSVR的参数估计精度最高,SVR次之,LSR最低;在运行时间方面,LSR由于无需进行模型内的参数寻优速度较快,LSSVR次之,SVR 较差。当样本量变化时,随着样本量的减小,3种参数估计方法的精度均呈现减小的趋势。但LSSVR的参数估计精度受样本量变化的影响最小,具有较高的稳定性。可知,当飞机IDG的故障数据为小样本时,采用LSSVR可获得较为客观准确的可靠性参数估计结果。

根据本文研究结果可为航空维修单位制定飞机IDG相关维修计划提供理论依据,以节约维修成本提高飞机的使用效率;此外,该小样本故障数据情况下的可靠性参数估计方法还可以为飞机其他系统、附部件以及其他领域的高可靠性装备提供参考依据。