增强经验小波分解和自组织深层网络在轴承工况识别中的研究
2022-06-27张康智毕永强曹鹏飞
张康智,毕永强,曹鹏飞
(1.西安航空学院 机械工程学院,西安 710077;2.西安兴航航空科技股份有限公司,西安 710077)
滚动轴承的运行工况影响着整机的工作性能,及时地对滚动轴承进行状态监测与工况识别,对于保证整机的运行安全,具有重要意义[1]。然而,实际采集到的轴承振动数据受噪声干扰严重,且存在一定的非线性和非平稳性。因此有必要对采集得到的轴承振动数据进行预处理以增强工况特征信息,从而获得更好的工况识别结果。
深度学习[2]能自动从轴承振动数据中学习本质特征,克服了传统“特征提取+模式识别”方法的缺陷[3],在轴承工况识别领域取得了较大突破。Shao等[4]在缺少轴承工况信息的情况下,使用深层玻尔兹曼机取得了较高的工况识别准确率;Shao等[5]提出深层特征融合方法,增强了深层网络的轴承振动数据特征学习能力。上述基于深层模型的轴承工况识别研究取得了一定的成果,但仍存在以下缺陷:1)模型在训练过程中结构固定不变,这将会导致基于确定结构的深层模型难以处理滚动轴承这种非线性和非平稳性振动信号[6]。2)若直接将带噪声轴承振动数据输入深层网络,噪声的存在会降低工况识别准确率且还会导致深层网络的收敛速度变慢。在众多信号降噪方法中,EMD[7]、EEMD[8]、LMD[9]等模态分解降噪方法缺乏严格的数学理论基础;VMD[10]具有较为坚实的数学理论,但分解模态个数难以确定;经验小波分解(Empirical wavelet decomposition,EWD)[11]具有较为完备的数学理论,分解结果较稳定,但难以对频谱边界进行有效检测。
针对经验小波分解和深度学习的优势,提出一种基于EEWD和SODN的滚动轴承工况识别方法,实验结果表明该方法具有较好的可行性和有效性。
1 增强经验小波分解
1.1 EEWD
经验小波分解对轴承振动信号的频谱边界进行有效检测和分割,然后建立小波滤波器提取相应的调幅-调频成分,从而将信号分解为若干个本征模态函数(Intrinsic modal functions,IMF)之和,但目前存在的几种信号频谱边界检测法均存在较大的缺陷。本文中提出一种新的经验小波分解频谱分割方法,考虑频谱形状,使用最大值滤波器的包络寻找主频值,筛选有效的频率峰值准则如下:
准则1 包络平顶频谱宽度要大于统计滤波器尺寸。
准则2 有效包络平顶不能出现在信号频谱的下降趋势段。
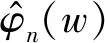
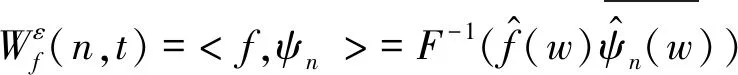
(1)
(2)
重建公式如下
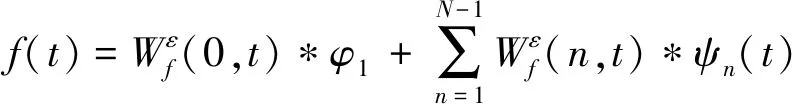
(3)
式中*代表卷积操作。信号f(t)可被分解为:
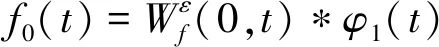
(4)
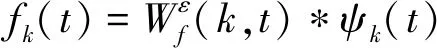
(5)
式中k=1,2,…,N-1。
采用仿真信号进行分析,即:
(6)
式中:f1(t)为余弦信号;f2(t)、f3(t)为调频信号;f4(t)为调幅-调频信号;f5(t)为白噪声。
分别采用EEWD和原始EWD对f(t)进行分解,分解结果如图1和图2所示,并取与原信号相关性较强的前4层进行重构分析,时频谱分别如图3和图4所示。可见,原始EWD产生了较为严重的模态混叠效应,频谱杂乱;而EEWD能较准确地分解仿真信号,对噪声鲁棒性较强。

图1 EEWD分解结果
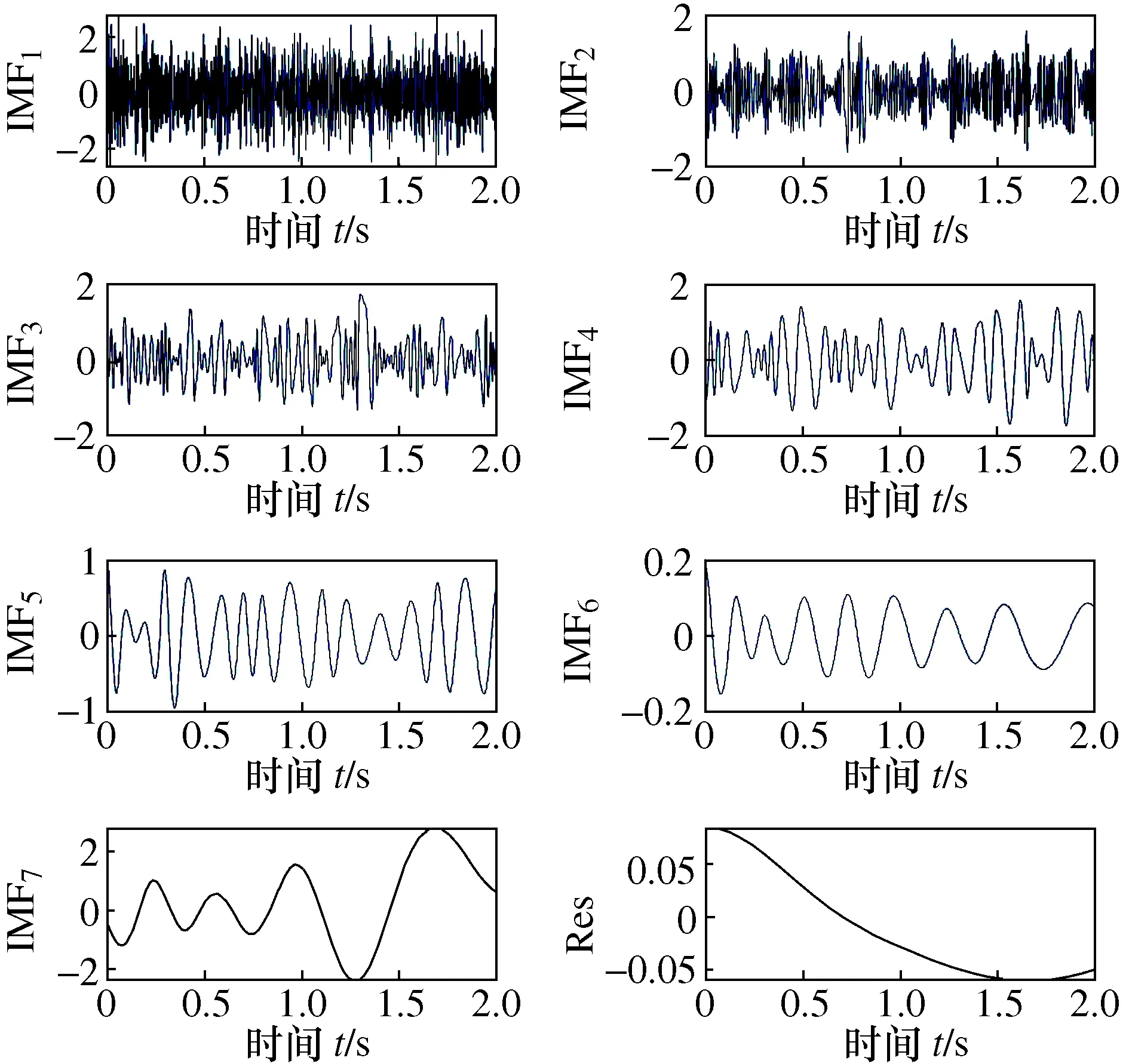
图2 原始EWD分解结果
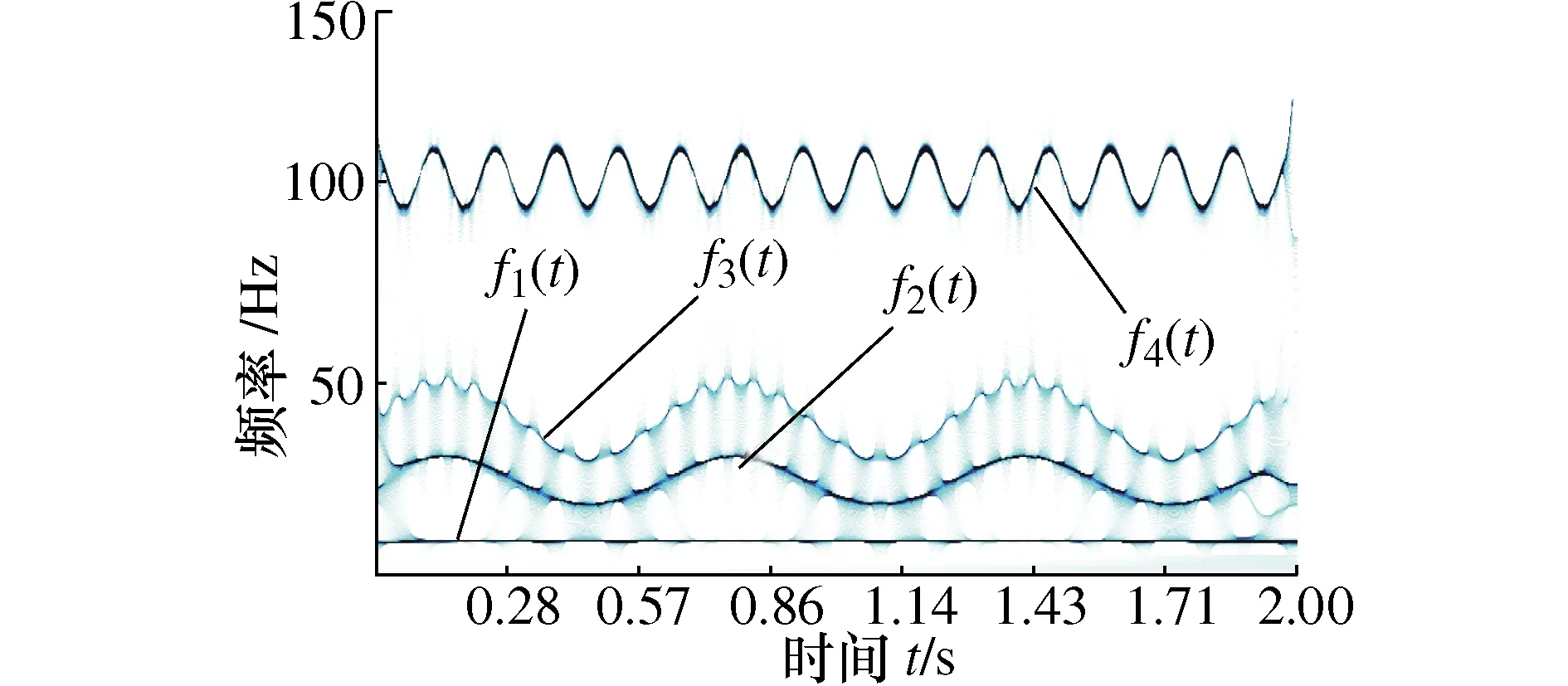
图3 EEWD时频图
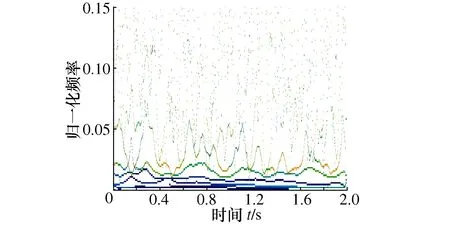
图4 原始EWD时频图
1.2 综合评价指标
使用综合评价指标对EEWD分解的信号进行选择性重构,表达式为:
P=ηKr+φrxy+ξexy
(7)
η+φ+ξ=1
(8)
式中:φ,η,ζ均为比例系数,取值为0~1;Kr为峭度,值越大,表明信号中周期性冲击成分比重越大;rxy为相关系数,值越大,表明各模态与原始信号相关程度越大;exy为能量比,可剔除EEWD因能量泄漏引入的附加成分。经反复实验,取各指标为相同权值,选择P最大的前4个分量进行重构,这样具有较好的稳定性。
2 自组织深层网络
2.1 小波卷积网络
小波自编码器兼具自动编码器的无监督特征学习能力和小波的时频聚集特性,其结构如图5所示。
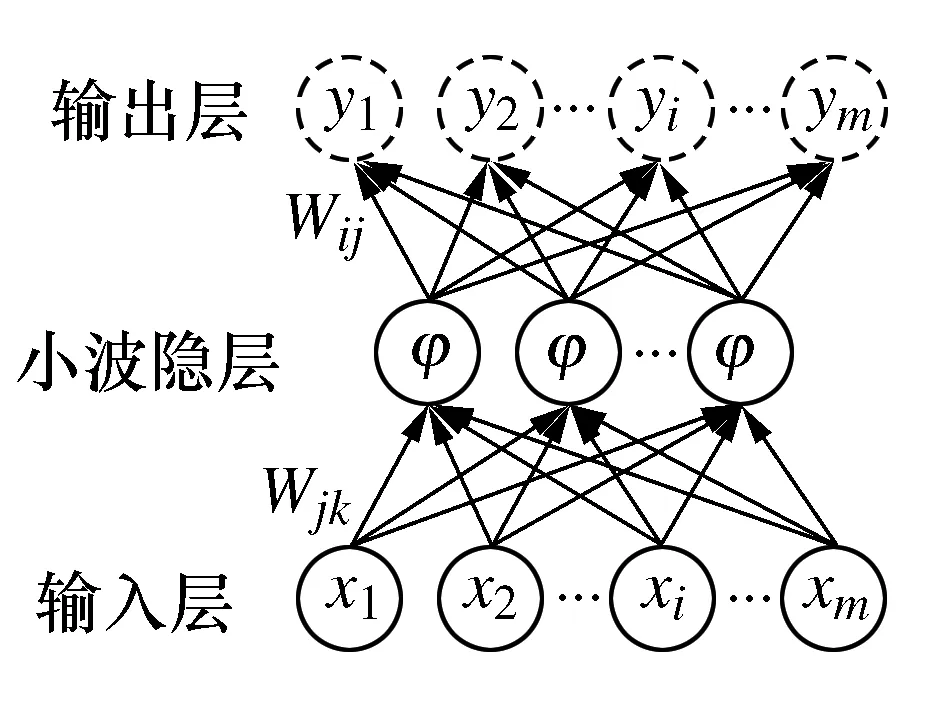
图5 小波自编码器
小波自编码器为全连接网络,参数众多,训练速度慢,且学习到的特征不具备平移不变性;卷积网络具有稀疏连接特性,学习到的特征在位移、尺度上具备较好的不变性。因此本文将小波自编码器和卷积网络结合,构造小波卷积网络。设网络的输入为x,则网络隐层第k个节点输出如下:
hk=ψ[(x*Wk-ck)/ak]
(9)
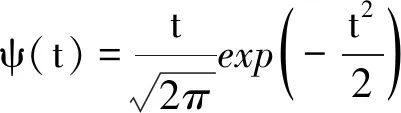
(10)
式中:ψ为高斯小波;Wk为卷积核权重;ak和ck分别为网络隐层小波节点的尺度和平移向量。重构信号为
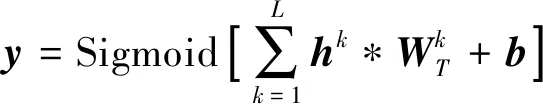
(11)
式中:L为隐层节点个数;WTk为反卷积核权重;b为偏置。
深层小波卷积网络堆叠多个小波卷积网络,能进一步提高网络学习到的特征的质量,首先,利用无标签的轴承振动数据训练第一层小波卷积网络,得到第1隐层特征;其次,将第1隐层特征输入第2层小波卷积网络,得到第2隐层特征,以此类推;最后,利用少量带标签样本对整个网络有监督微调。
2.2 自组织深层网络
深层小波卷积网络在训练过程中结构固定不变,这将会导致基于确定结构的深层模型难以处理滚动轴承这种非线性和非平稳性振动信号,因此引入自组织策略,使网络结构在训练过程中自适应动态变化,更适用于非线性和非平稳性轴承振动信号。自组织策略基于网络节点激活值和损失函数梯度下降率最小化。首先,在预训练阶段将隐层节点激活强度作为节点“贡献度”,并根据“贡献度”大小对节点进行增加或删减;然后,在微调阶段,当损失函数梯度下降率首次出现递减时删掉一个隐层,否则增加一个隐层,激活强度S计算为
(12)
式中:α为常数,α>0;oi.l为第l个隐层的第i个节点的输出;Nl为第l个隐层节点个数;si.l为第l个隐层的第i个节点的输入权值之和。
(13)
式中:rij为第i个节点的第j个输入;wij为第j个节点和第i个节点的连接权重。自组织策略见图6。

图6 自组织策略
整体轴承工况识别步骤如下:
1) 采集不同工况的轴承振动信号,随机选取80%作为训练样本,其余为测试样本;
2) 对样本进行EEWD分解,并利用综合评价指标对IMF分量进行信号重构;
3) 将重构后的训练样本输入SODN进行无监督预训练和有监督微调训练;
4) 使用测试样本对训练好的网络进行测试。工况识别方法流程图如图7所示。
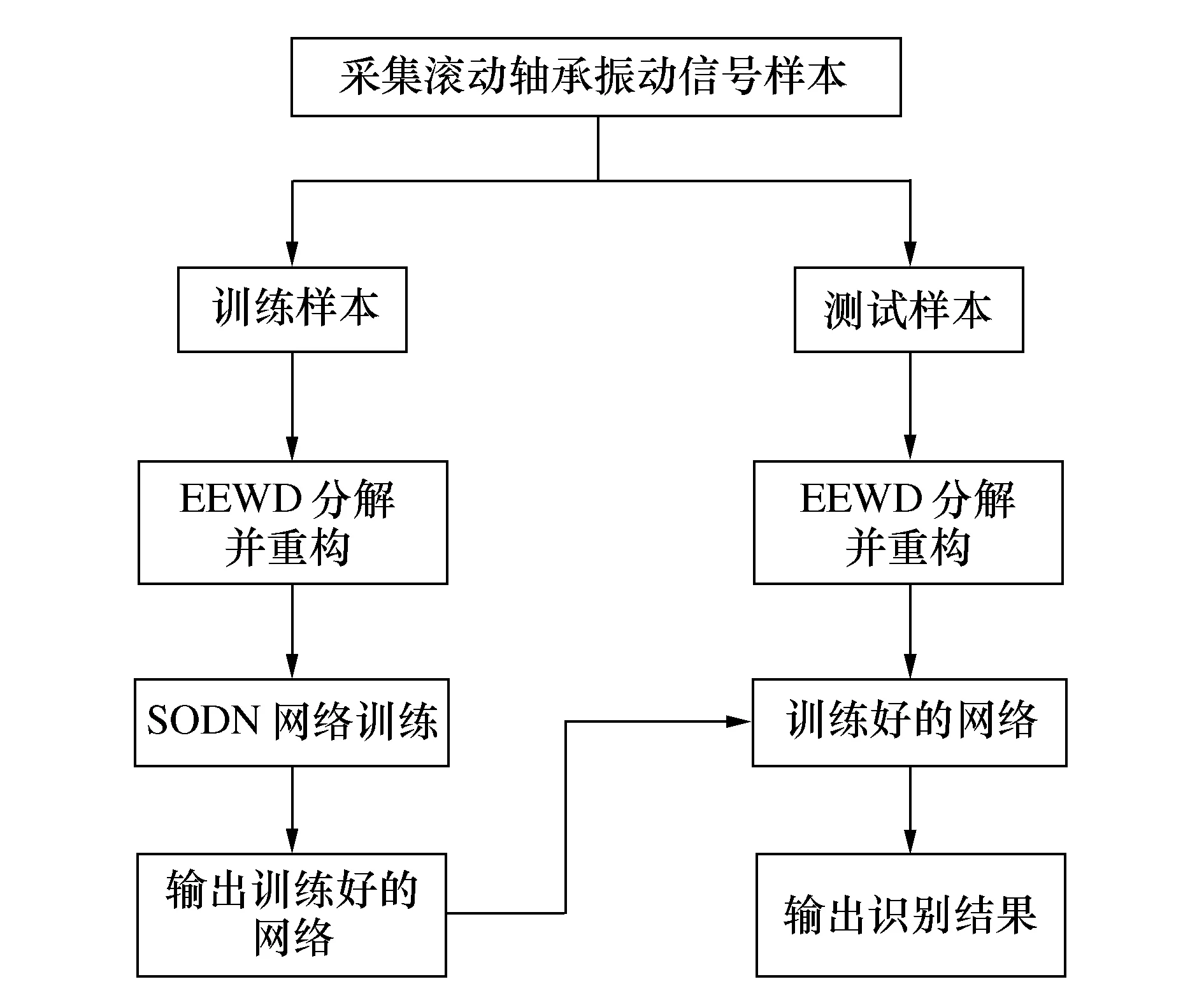
图7 工况识别流程图
3 实验验证
3.1 实验数据描述
为验证算法的可行性和有效性,以XJTU-SY滚动轴承试验数据集[13]为对象。试验台如图8所示,由交流电动机、转速控制器、转轴和测试轴承等组成。

图8 轴承测试实验台
限于文章篇幅,在XJTU-SY数据集中选取7种不同的轴承运行工况,见表1。
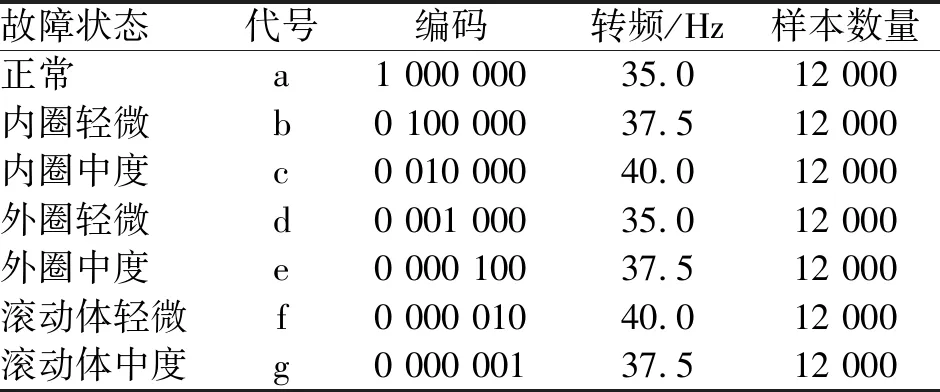
表1 7种滚动轴承工况
图9为7种滚动轴承工况的时域图,可知信号受噪声干扰严重,难以对轴承运行工况进行有效区分。
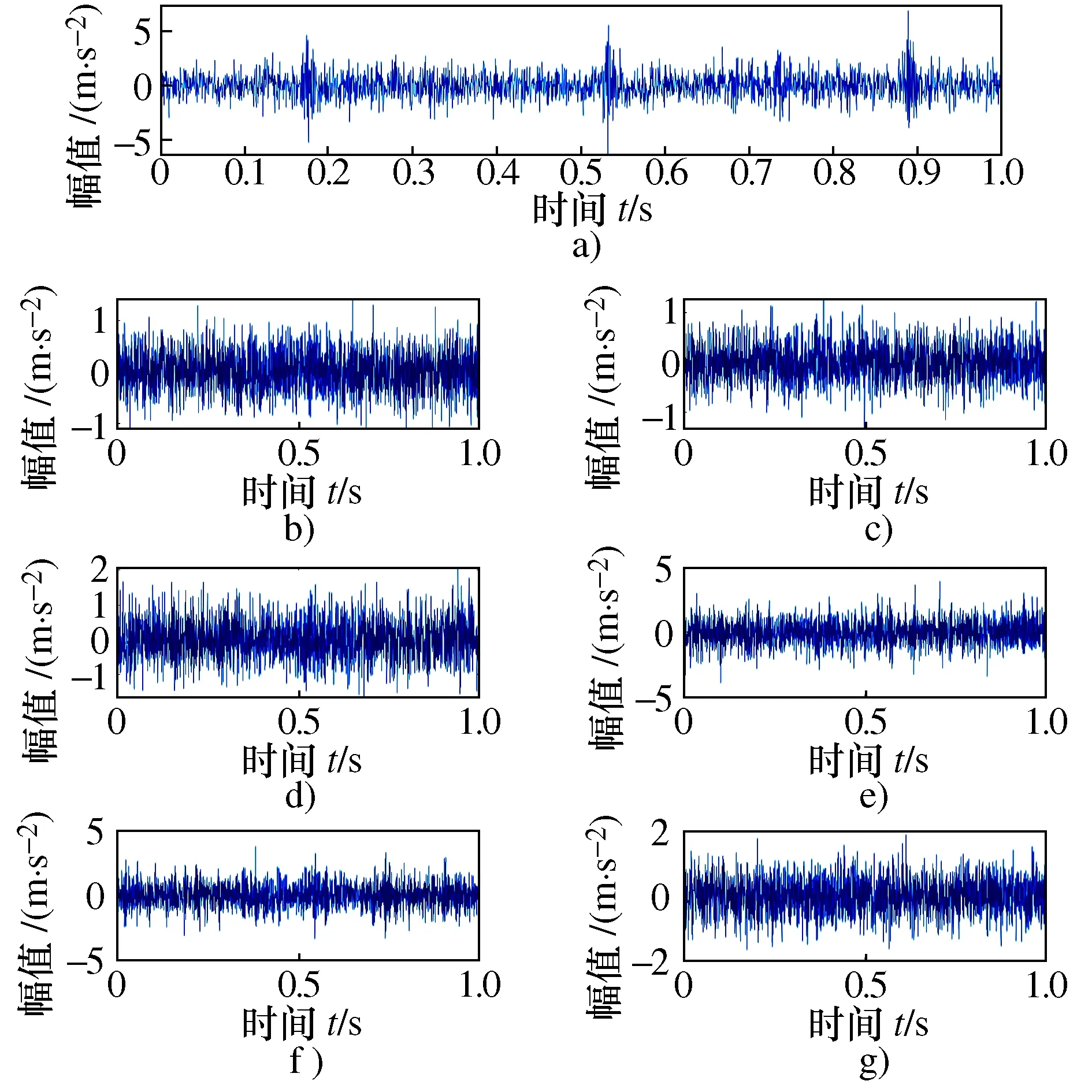
图9 滚动轴承7种工况的时域图
3.2 实际信号分解效果对比
以XJTU-SY数据集中轴承外圈轻微故障振动信号为例,分别采用EEWD和原始EWD对其进行分解,如图10和图11所示。可见,原始EWD分解结果模态混叠严重,干扰过多;而EEWD分解模态数明显小于原始EWD,根据综合评价指标,对信号重构并进行相应的时频变换,如图12和图13所示。

图10 EEWD分解结果
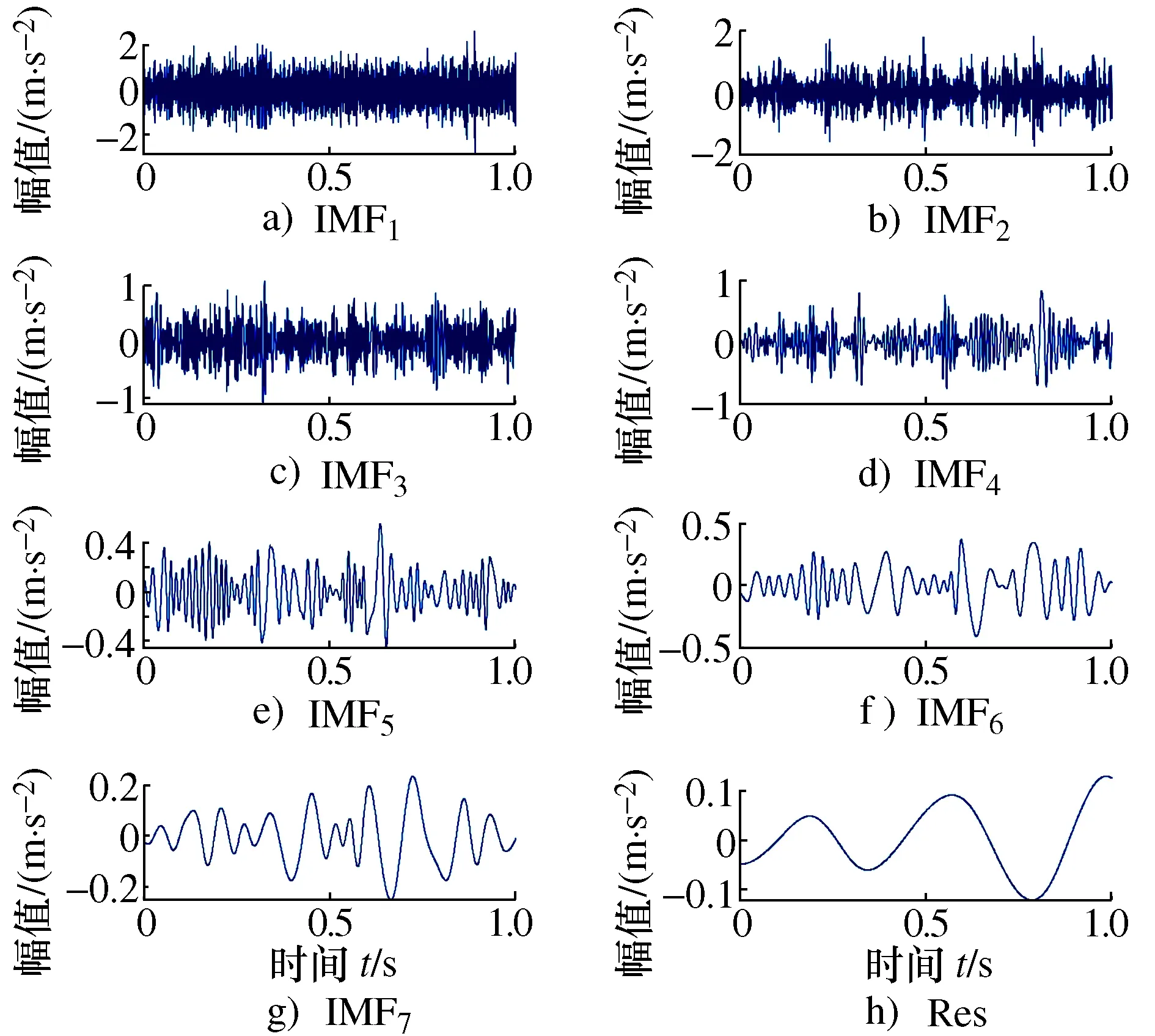
图11 原始EWD分解结果
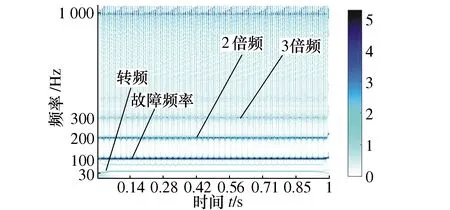
图12 EEWD时频图
(14)
式中:d为滚子直径;D为节圆直径;a为接触角;Z为滚子数;fr为转频30 Hz。
从IEWD时频谱中可以比较清晰的看出故障外圈故障频率以及倍频,验证了EEWD的有效性。
3.3 工况识别与分析
为证明本文方法的优越性,采用深层自动编码器(Deep auto-encoder,DAE)、深层稀疏编码器(Deep sparse auto-encoder,DSAE)、深层降噪编码器(Deep denoising auto-encoder,DDAE)、深层收缩编码器(Deep contractive auto-encoder,DCAE)和深层小波编码器(Deep wavelet auto-encoder,DWAE)等方法进行对比分析,输入均为EEWD分解重构后的1 024维信号样本,超参数均由文献[14-15]所提方法确定,如下:
1) SODN(本文方法):SODN初始结构为1 024-512-256-128-64-32-7,每个小波卷积网络的学习率和迭代次数分别为0.05和200。
2) DAE:DAE结构为1 024-512-256-128-64-32-7,每个自编码器的学习率和迭代次数分别为0.05和200。
3) DBN:DBN结构同DAE,每个RBM的学习率和迭代次数分别为0.05和200。
4) DDAE:DDAE结构同DAE,Dropout率取0.2,每个自编码器的学习率和迭代次数分别为0.05和200。
5) DSAE:DSAE结构同DAE,稀疏因子取0.2,每个自编码器的学习率和迭代次数分别为0.05和200。
6) DCAE:DCAE 结构同DAE,收缩因子取0.1,每个自编码器的学习率和迭代次数分别为0.05和200。
7) DWAE:DWAE结构同DAE,取高斯小波作为激活函数,每个编码器的学习率和迭代次数分别为0.05和200。
共进行10次试验,表2列出了各方法的平均识别精度和训练时间,图14为每次试验结果。

表2 不同方法的识别结果
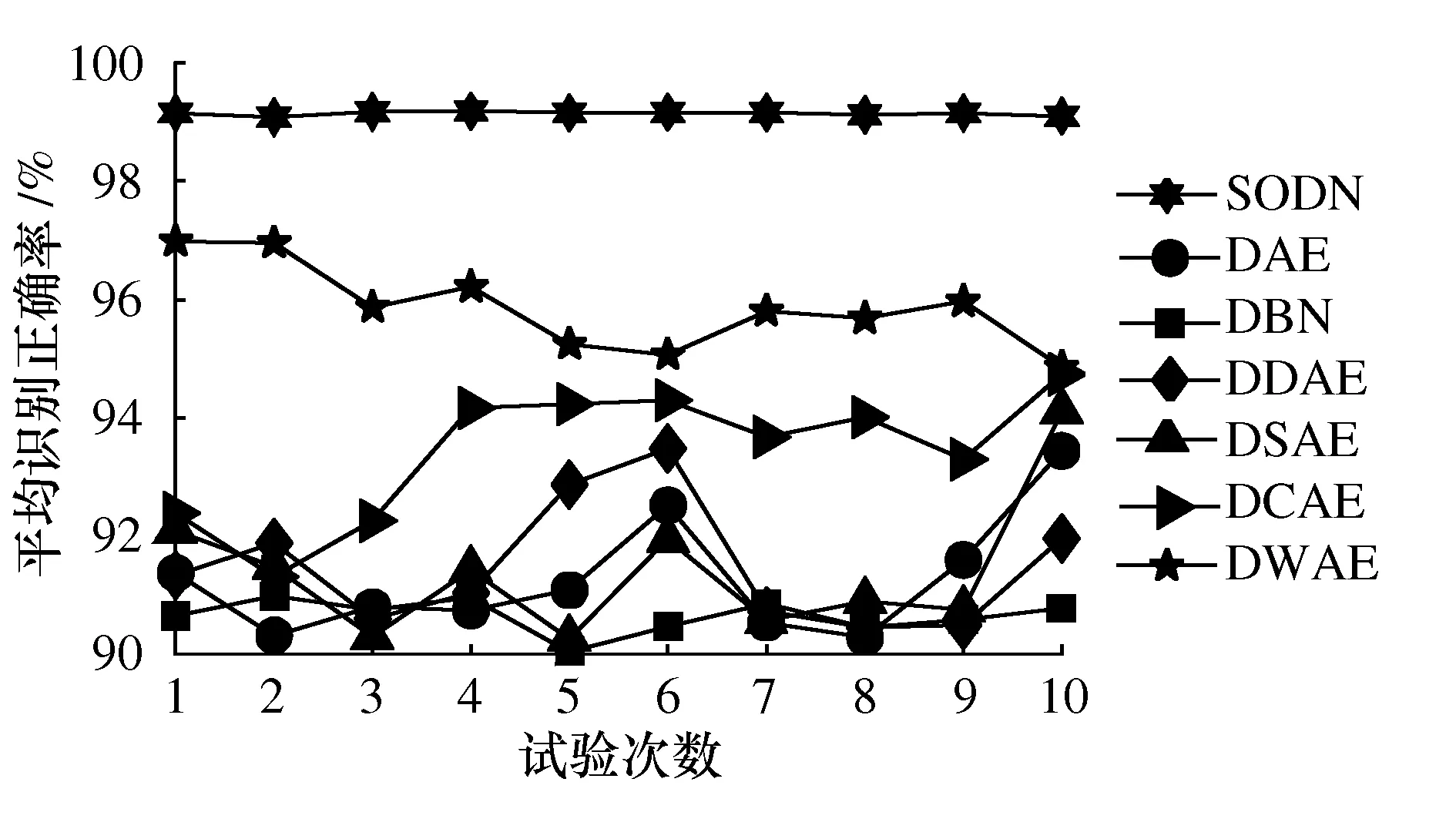
图14 不同方法的10次测试结果
由表2可知,SODN利用自组织策略确定较优的网络结构,使网络具有更高的识别准确率(98.93%)和更小的标准差(0.11),DAE的故障识别率最低;DSAE加入稀疏项限制,可捕捉输入数据的较重要的信息;DDAE可提高网络对噪声的鲁棒性;DCAE加入收缩性限制,使网络对输入信号在一定程度下的扰动具有不变性;DWAE使用小波作为激活函数,具备一定的时频聚焦特性,能有效学习轴承振动信号的时频特征,综上,DSAE、DDAE、DCAE和DWAE的故障识别效果均优于DAE,但均低于SODN模型。
3.4 不平衡数据集下的识别准确率
实际工业中,正常样本所占比例通常较高,本节研究SODN模型在面对不平衡样本时的有效性,共设计4种数据集,比较5种不同方法(DWAE、DCAE、DSAE、DDAE和SODN)的性能。设置正常与各故障工况的训练样本比例分别为12000∶10000、12000∶8000、12000∶6000和12000∶4000,实验共进行10次,5种方法的识别准确率如图15所示。
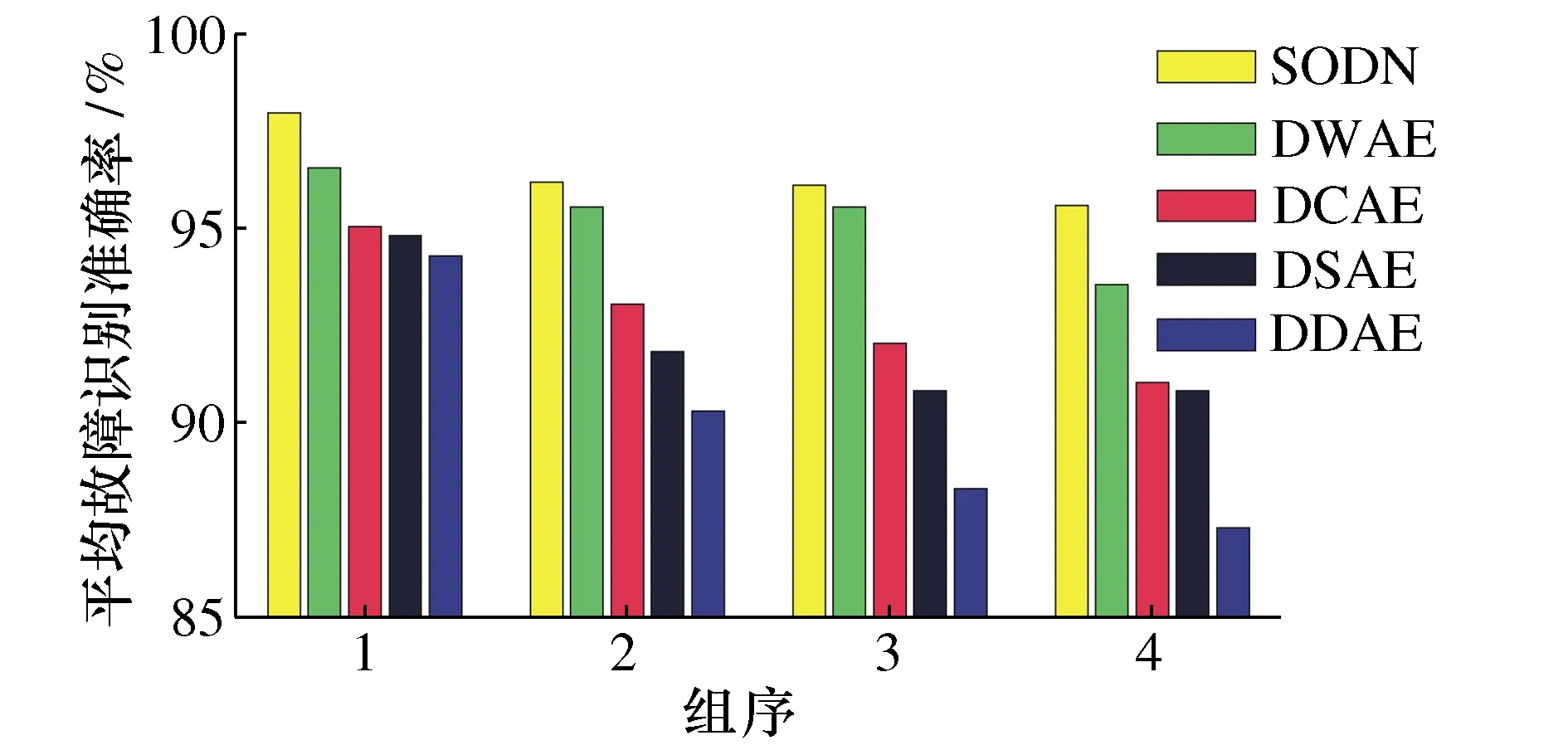
图15 不平衡样本下5种方法的识别准确率
由图15可知,5种方法的平均识别准确率随不平衡比例的增大整体呈现下降趋势,但本文方法相较于另外几种方法表现更加优异,具有更高的泛化性能。还定量计算了几种方法基于不平衡数据集的精确率P、召回率R和F1值,表达式分别为:
(15)
式中:TP为正样本中被模型判断为正的个数;FP为在负样本中被模型判断为正的个数;FN为正样本中被模型判断为负的个数;F1值在[0,1]之间,反映查准率和召回率的信息,0代表最差,1代表最好。以第4组为例,表3列出了第4组中3种方法的精确率和召回率,表4列出了相应的F1值。
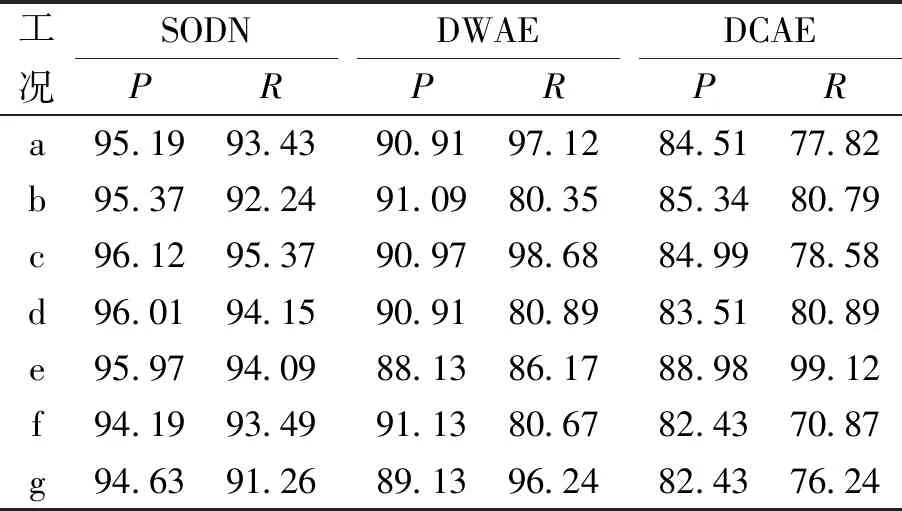
表3 第4组不同方法的精确率和召回率
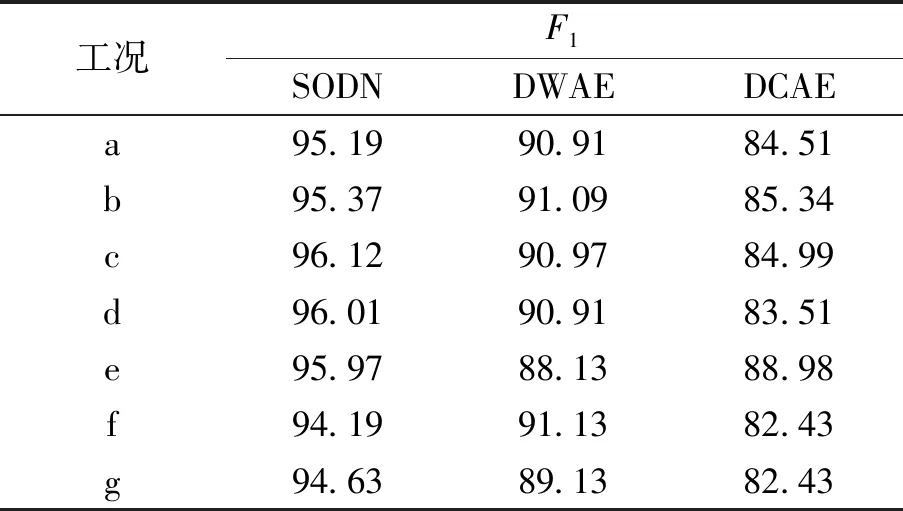
表4 第4组不同方法的F1值
由表3和表4可知,第4组中SODN的P、R和F1指标值均较高,类似的结果在其他组中也有较为明显的体现,这些对比结果进一步验证了SODN在面对不平衡数据集时的有效性。
3.5 不同激活函数对SODN识别准确率的影响
激活函数对SODN的性能有一定影响,本节讨论几种不同激活函数对SOAECN识别准确率的影响,几种激活函数的方程及相应的平均识别准确率如表5所示可知,Gaussian小波、Morlet小波和Mexican hat小波的故障识别效果好于其他激活函数,Gaussian小波在时域、频域均有良好的分辨率,取得了最好的识别结果。
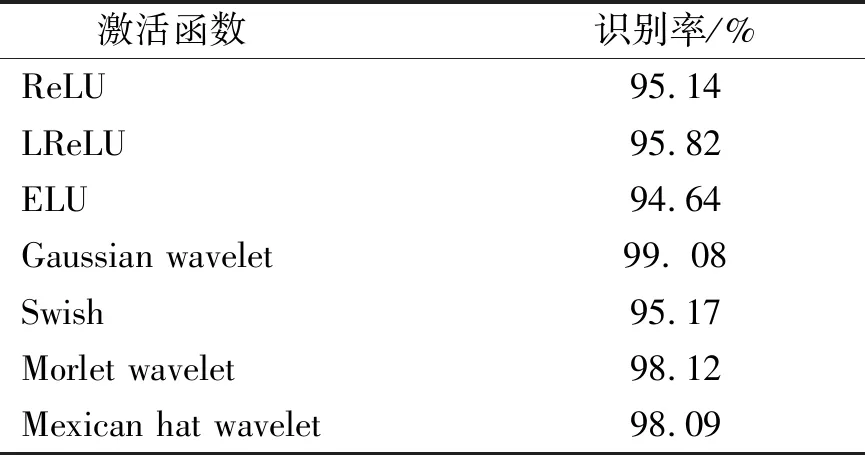
表5 不同激活函数对识别准确率的影响
4 结论
1) 提出的EEWD能自适应划分轴承振动信号频谱的边界,自动确定分解模态数,利用综合评价指标进行IMF的选取,重构效果较好。
2) 提出的小波卷积网络具有稀疏连接特性,学习到的特征在尺度、位移上具有不变性;并将自组织策略用于小波卷积网络,使网络结构在训练过程中自适应动态变化,使网络更适用于非线性和非平稳性轴承振动信号。
