考虑经济相关性的复杂二维保修装备组合维修策略

董恩志, 程中华, 王荣财

(1. 陆军工程大学石家庄校区, 河北 石家庄 050003;2. 河北省机械设备状态检测与评价重点实验室, 河北 石家庄 050003)

0 引 言

随着新军事技术和理论不断创新,一大批性能先进、系统性强的复杂装备陆续列装部队。在列装部队的复杂装备中,有大量装备的寿命受日历时间、使用程度等因素的共同影响,即过久的使用时间或过高的使用强度都会加快装备部件的退化速度。二维保修服务所涵盖的变量数量通常包括日历时间和使用程度,如某型高炮有长达3年与250 000公里的二维保修期。复杂装备的编配极大提高了部队的作战效能,但由于部队难以在短时间内形成自主保障能力,因此完全依靠建制力量完成复杂装备的维修保障面临较大困难。将承制单位这一地方维修保障力量纳入新型复杂装备的维修保障体系之中的方式,在实际运作过程中缺乏具体的决策技术支持,使部队在装备保修期内的保修成本支出较大,保修效果不够理想。

除此之外,复杂装备大多技术先进、内部结构复杂,包含众多多部件系统,保修服务通常针对多部件系统展开。多部件经济相关是指对系统部件的维修工作进行组合后,系统的保修费用高于或低于分别保修费用之和。

本文选择串联多部件系统为研究对象,在保修期内若孤立地对各单部件进行维修,会出现频繁停机等情况,浪费维修资源,增加预防性维修准备费用的支出,因此采用恰当的组合维修策略可大幅缩减其保修期内的保修费用。

本文的研究目标是使保修期内的保修费用最低,若达到此要求,则表明本文所建立的模型有效。保修期内保修费用的影响因素包括保修方式和维修策略。保修方式包括一维保修、二维保修等;维修策略包括修复性维修、预防性维修、组合维修等。本文拟采取的保修方式为二维保修,采取的维修策略为不完美预防性维修与组合维修。在实例分析部分,通过与其他保修方式或维修策略下的保修费用比较,验证本文所建立模型的优越性。本文结合装备保障实际,研究了二维预防性维修服务下新型复杂装备组合维修策略,用以降低保修期内部队的保修费用,减少军地双方的利益冲突,优化保修效果。

1 二维保修研究现状分析

1.1 二维保修决策模型研究现状

二维保修的特征是保修期包含日历时间与使用程度两个变量,通常可由二维平面上的一块区域表示,保修政策会引起保修区域形状的变化,Wang等详细梳理了二维保修政策及其对应的保修区域形状。二维保修的研究思路一般为:先确定二维保修区域,然后将其划分为若干子区域,确定各子区域的维修方式,以保修费用、可用度、费效比等为目标建立优化模型。文献[10-13]等都按照上述思路进行研究,依据不同的优化目标进行建模。近几年,二维保修研究又呈现出一些新的趋势:Peng等开发了一个随机动态的维修模型,随机和动态使用率直接影响预防性维修决策;文献[15]为双渠道(线上与线下)销售厂家制定了一种使用价值风险方法同时优化二维保修政策和定价。在充分考虑了保修服务对象异质性的基础上,文献[16-19]为不同客户量身定做二维保修服务;文献[20-22]在二维保修服务中采用预防性维修措施,用以降低保修费用,提高可用度。从历史索赔数据中获取关键信息作为建模的依据,文献[23-25]研究了数据驱动的二维保修决策模型。通过文献回顾可以看出,当前对二维保修的研究越来越关注消费者的利益诉求与产品的多样性,也逐步凸显了保修数据的重要性。此外,由于预防性维修能够预防故障或故障的严重后果,减少因故障停机造成的损失,也越来越受到研究者的重视。

但是,当前对于复杂多部件系统二维保修策略的研究较少,在一定程度上脱离了工程实践。

1.2 多部件系统经济相关性研究现状

针对复杂多部件系统的经济相关性问题,学者们从不同角度开展研究:文献[26]提出了一种考虑经济依赖和状态依赖检查间隔的多状态串并联系统维修优化方法;针对具有随机和经济相依关系的两部件系统,文献[27]提出了一种基于状态的维修策略模型; Dao等探索了部件经济相关的多状态串并联系统的选择性维修策略的制定:决策者可以根据维修目标、资源可获得性以及每个部件的维修时间和成本,选择不同的部件进行维修以降低维修成本;苏春等考虑了风力机部件之间的经济相关性,基于更新过程理论建立状态维修策略下长期运行平均成本率模型,分析出多部件系统最优检测周期。文献[30]考虑了多部件串联系统的维修分组方法,在维修时间与维修人员均有限并随时间变化的条件下得到系统最优的维修计划。文献[31]提出一种退化状态空间划分方法，用于具有经济相关性的相同多部件系统的机会维修建模,为具有相同部件的多部件系统的维修优化提供了一种新的广义建模方法。可以看出,复杂多部件系统的保修研究中,多部件之间的经济相关性较为受研究者关注,分别从不同角度给出维修工作的组合策略,但是,这些研究都是采用的一维保修方式,考虑经济相关性的二维保修策略的研究很少。文献[32]为了降低二维保修期内的保修费用,将多部件的预防性维修工作进行了组合优化,研究区分了用户和厂家进行预防性维修的修复因子,而在实际中开展预防性维修经常由用户或厂家独立进行,这种联合开展的情况较少。除此之外,该研究缺乏与其他保修方式或维修策略的对比分析,导致模型的优劣难以直观体现出来。

针对现有研究的不足,本文研究包含多部件系统的复杂装备的二维预防性维修策略,并在此基础上考虑多部件系统的经济相关性,研究二维预防性维修策略下串联多部件系统组合维修策略。通过建立单部件二维预防性维修费用模型,得到使保修费用最低的最优预防性维修间隔期,将不同部件之间的预防性维修工作进行组合,重新设置各单部件的预防性维修间隔期,降低保修期内部队的保修费用。本文可为二维预防性维修服务下复杂装备组合维修策略的制订提供科学依据与定量化分析方法。

2 模型描述与假设

2.1 模型描述

本文以串联多部件系统为研究对象,部件按照间隔(0,0)进行预防性维修。其中，0表示部件在时间维度的预防性维修间隔期,0表示部件在使用程度维度的预防性维修间隔期。部件使用时间和使用程度有一个达到0或0则开展预防性维修。以二维保修期(,)内单部件预防性维修费用模型为基础,借助预防性维修基准间隔期,将各单部件预防性维修工作组合优化,用以降低串联多部件系统保修的费用。

2.2 模型假设

(1) 复杂装备的某子系统由若干单部件串联组成。

(2) 各单部件均是可修部件,具有随时间和使用度两个维度同时退化的特性,故障率随使用期限增加而增加。

(3) 对各单部件执行定期预防性维修,全部由承制单位执行,维修程度为不完美维修,每次预防性维修之前都需支付一定的预防性维修准备费用,用 表示,部件单次预防性维修费用为。

(4) 相对于保修期长度,维修时间很短,忽略不计。

(5) 部件在两次不完美预防性维修间隔期之间故障后实行最小维修,全部由承制单位执行,部件单次最小维修费用为。

(6) 串联多部件具有相同的使用率分布,()为部件使用率的概率密度函数,其概率累积分布函数为()。

(7) 系统内多部件之间具有经济相关性,在同一时刻进行多个部件的预防性维修工作,只需缴纳一次预防性维修准备费用。如果孤立地开展各个部件预防性维修工作,会导致系统频繁停机,产生大量的预防性维修准备费用。各个部件的预防性维修工作组合之后,将会减少系统的停机次数,减少预防性维修准备费用的缴纳,保修期内的保修费用支出将会减少。

3 模型构建

3.1 故障率模型

一般来说,系统的可靠性与使用率关系密切,在设计阶段,可靠性指标是在一定的使用强度下设计的,因此在使用阶段,使用率的变化必然会导致可靠性及故障函数的变化。基于此,本文在加速失效时间(accelerated failure time, AFT)模型的基础上构建部件的故障率函数。Lawless利用AFT的概念和比例风险模型来构造使用率对系统故障的影响,该方法具有一定的理论基础且应用较为成熟。

假设和分别表示在设计使用率和使用率下首次故障的时间,则其关系可表示为

(1)

假设(;,)为在设计使用率下的累计故障分布函数。其中,设计使用率下故障分布的尺度参数和形状参数分别用和表示。在使用率为时,系统累计故障分布函数与设计使用率下系统的累计故障分布函数有形式相同,但是尺度参数发生了变化:

(2)

其中,AFT参数≥1。基于此,使用率为时系统的累计故障分布函数可以表示为

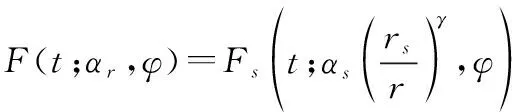
(3)

由于形状参数不随使用率的变化而改变,因此在以下表达式中将其省略。使用率为时系统的故障率函数为

(4)

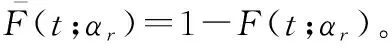
(5)

3.2 单部件二维预防性维修费用模型

本文采取的维修策略为:在预防性维修间隔期内的故障采取最小维修,部件最小维修后故障率不变;预防性维修为不完美预防性维修,部件在维修后介于“修复如新”与“修复如旧”之间。本文运用“虚拟工龄方法”对不完美预防性维修进行建模,其基本思想为:预防性维修降低了部件或系统的故障率,提高了系统或部件的性能,如同部件或系统的年龄向前推移了一段时间。引入改善因子(用表示)描述不完美预防性维修的效果。假设部件的改善因子受部件的实际工龄、不完美预防性维修间隔期0和单次不完美预防性保修费用的影响,则改善因子可表示为

(6)

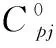
第次不完美预防性维修后,部件或系统的故障率下降到维修前0时的故障率,因此,部件或系统的故障率为

(7)

其中,(;)表示部件在使用率下的第次与第+1不完美预防性维修之间的故障率函数。图1演示了部件进行不完美预防性维修时故障率函数的变化情况。

图1 不完美预防性维修下故障率变化Fig.1 Failure rate change under incomplete preventive maintenance

图1中,表示部件在第次不完美预防性维修后的虚拟工龄。由于装备的保修期限是二维的,即(,),预防性维修间隔期不是确定值,因此由预防性维修间隔期导出的使用率0存在不确定性,建模时应分两种情况讨论,分别是0≤与0>。

(8)

因为实际使用时使用率不是定值,因此保修期限会出现不同情况。具体来说,当实际使用率较低时,如图2中所示,保修期限为[0,);当实际使用率较高时,如图2中所示,保修期限为[0,)。

图2 不同使用率对应的保修期限Fig.2 Warranty period corresponding to different usage rates

基于不同的保修期限,不完美预防性维修的次数又有4种情况,如表1所示。其中，int表示向下取整。

表1 不同期限下不完美预防性维修次数

(1) 当0≤时。如图3所示,在这种情况下又要区分≤0,0<≤和>3种不同情况。部件的预防性维修间隔为0，在二维保修期下部件的预防性维修次数为。

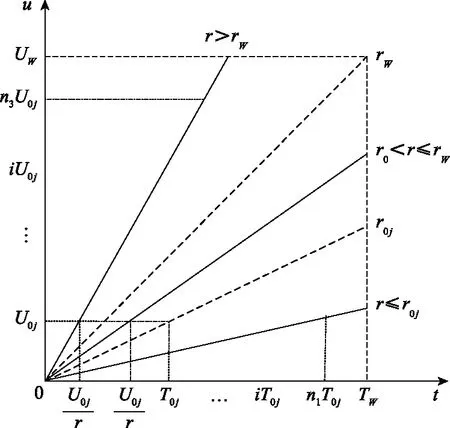
图3 二维不完美预防性维修周期(r0j≤rW)Fig.3 Two-dimensional incomplete preventive maintenance cycle (r0j≤rW)

部件的期望保修费用包括两部分:总预防性维修费用和总故障后维修费用,分别用和 表示。当≤0时,保修期内部件期望保修费用为

= +=(+ )·+

(9)

当0<≤时,部件的预防性维修间隔期为0,在二维保修期下预防性维修次数为。保修期内部件的期望保修费用为

= +=(+ )·+

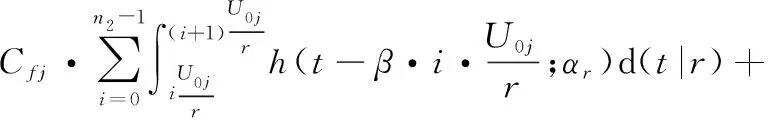
(10)

当>时,部件的预防性维修间隔期为0,在二维保修期下预防性维修次数为。保修期内的期望保修费用为

= +=(+ )·+

(11)

那么,在保修期(,)内,当0≤时,部件的总期望保修费用:

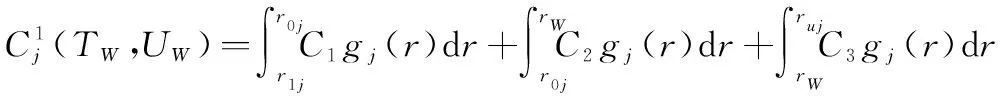
(12)

其中,1为部件使用率的下限;为部件使用率的上限。

(2) 当0>时。如图4所示,当≤时,部件的维修间隔期为0,在二维保修期下预防性维修次数为。

图4 二维不完美预防性维修周期(r0j>rW)Fig.4 Two-dimensional incomplete preventive maintenance cycle (r0j>rW)

部件的期望保修费用为

= +=(+ )·+

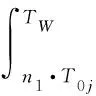
(13)

当<≤0时,部件的维修间隔期为0,在二维保修期下完整的预防性维修次数为。装备的期望保修费用为

= +=(+ )·+

(14)

当>0时,部件的预防性维修间隔期为0,在二维保修期下预防性维修次数为。部件的期望保修费用为

= +=(+ )·+

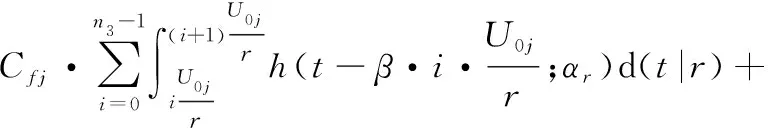
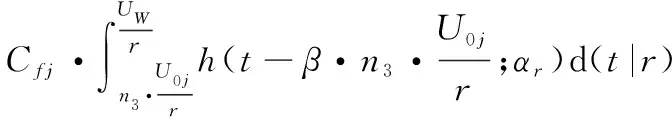
(15)

那么在二维保修期(,)内,当0>时,部件的总期望保修费用为

(16)

综合考虑以上两种情况,在保修期(,)内,当部件使用率服从一定的分布()时,在二维不完美预防性维修下,部件的总期望保修费用为

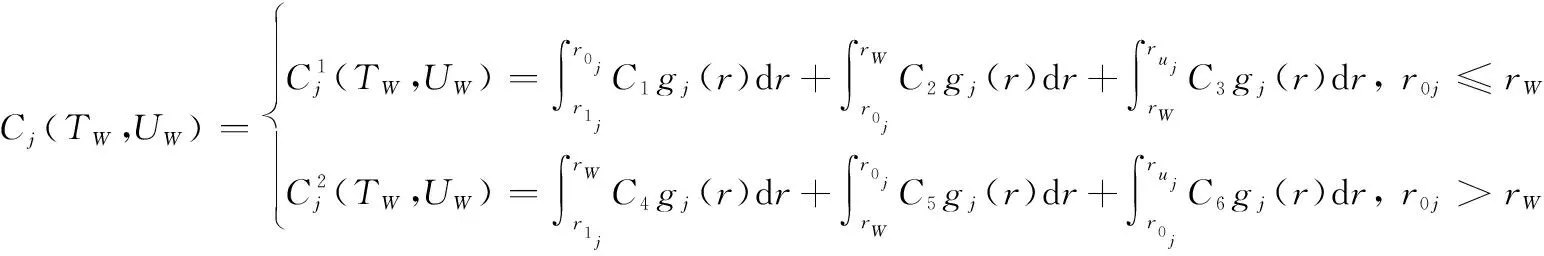
(17)

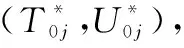
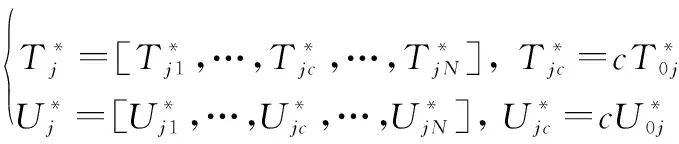
(18)

预防性维修组合之前,多部件系统的保修费用就是各单部件最优保修费用相加,即

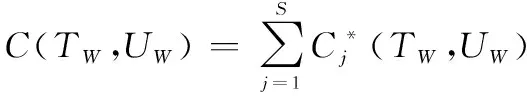
(19)

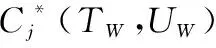
3.3 多部件系统二维预防性组合维修费用模型

由于每一次预防性维修都需要投入固定的准备费用,因此如果将各单部件预防性维修工作进行组合,可以减少二维保修期内多部件系统停机的总次数,降低预防性维修所需投入的准备费用。

基于此,引入预防性维修基准间隔期(,),分别为所有单部件最优预防性维修时间间隔期和使用程度间隔期的最小值,即

(20)

(21)

其中,[·]表示四舍五入后取整。

图5给出时间维度预防性维修工作组合优化的示意图。

图5 各部件预防性维修时刻优化Fig.5 Optimization of preventive maintenance time for components

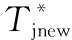
(22)

4 实例分析

批量列装部队的某新型防空导弹武器系统,其导弹发射车的动力装置属于二维保修串联多部件系统,可看作由3个单部件组成。在设计使用率下,单部件的累积故障分布函数为

(;)=1-exp[-()]

(23)

在使用率为时,单部件的累积故障分布函数为

(24)

单部件的故障率函数为

(25)

保修期内由承制单位对多部件系统内各单部件执行预防性维修,每次执行预防性维修部队都需要缴纳一定的维修准备费用,任一单部件出现故障,都会导致系统故障,部件之间存在经济相关性。对该动力装置各单部件预防性维修工作进行组合优化,实现降低保修费用的目标。该动力装置具有二维保修期，日历时间维度的保修期为3年，行驶里程维度的保修期为3×10公里。最低使用率为01×10公里年,最高使用率为10×10公里年。该动力装置使用率服从双参数威布尔分布,即:

(26)

其中,为尺度参数;为形状参数。其他参数如表2所示。

表2 参数设置

采用数值解法对单部件的二维预防性维修费用进行计算,具体的算法流程如图6所示。

图6 单部件二维预防性维修费用算法流程图Fig.6 Flow chart of single component two-dimensional preventive maintenance cost algorithm

如图6所示,令0以步长01年在[01年,3年]内取值,0以步长01万公里在[01万公里,3万公里]内取值,分别计算每一组(0,0)对应的保修费用(,),并储存。最终生成900组(0,0),分别对应不同的保修费用值。

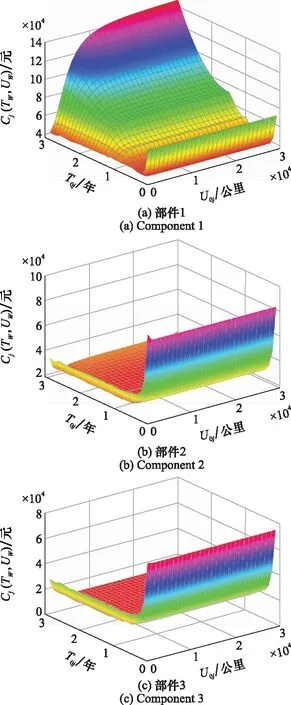
图7 各部件保修费用变化趋势Fig.7 Trend of warranty cost of each component

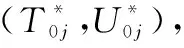
对各部件保修费用的变化趋势进行降维分析,研究某一维度的预防性维修间隔确定时,保修费用随另一维度预防性维修间隔期的变化趋势,如图8所示。图8(a)与图8(d)、图8(b)与图8(e)、图8(c)与图8(f)分别代表部件1～3,图8(a)～图8(c)展示了0取不同值时,各单部件保修费用随0的变化情况,图8(d)～图8(f)展示了0取不同值时,保修费用随0的变化情况。

图8 各部件保修费用变化降维分析Fig.8 Dimension reduction analysis of each component warranty cost

通过图8可以看出,单部件的保修费用随着预防性维修间隔期的变化而变化。固定任一维度的预防性维修间隔期,都存在另一维度上的最优预防性维修间隔期使部件的保修费用达到最低。对于部件2与部件3而言,当两个维度上的预防性维修间隔期都较小时,部件在保修期内进行的预防性维修次数变多,因此会产生较大的保修费用。当固定时,部件1的保修费用随的增加呈现先减少后增加的趋势,这主要是因为部件1的故障率与部件2和部件3相比较大,若长时间不进行预防性维修会增加修复性最小维修的费用,进而导致保修期内部件的保修费用增加。

4.1 采取一维保修与二维保修方式保修费用对比

引言中提到,影响保修期内保修费用的因素包括保修方式与维修策略,本文所采取的保修方式为二维保修。本节将对一维保修与二维保修下的保修费用进行对比,用以验证二维保修下预防性组合维修策略的优越性。两种保修方式下的维修策略相同,即均采取预防性组合维修策略。两种保修方式保修费用的对比如表3所示。

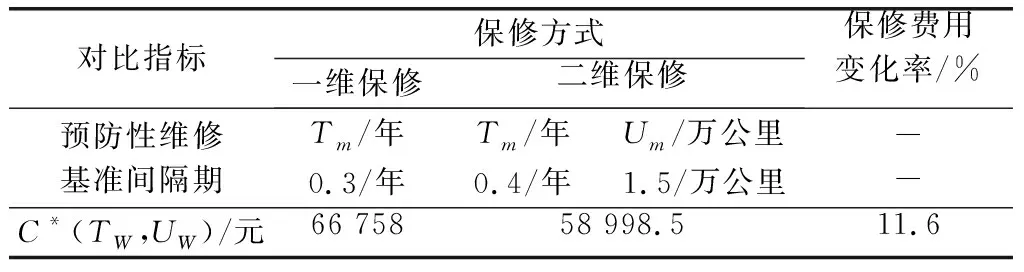
表3 一维保修与二维保修方式下保修费用对比

通过表3可以看出,如果该多部件系统采取一维保修方式,即仅在时间维度上考虑预防性维修工作,那么预防性维修基准间隔期为0.3年,组合后的保修费用为66 758元;如果该多部件系统采取二维保修方式,预防性维修基准间隔期分别为0.4年和1.5万公里,组合后的保修费用为58 998.5元。结果表明,采取二维保修方式可以节省部队保修期内的保修费用。

4.2 有无预防性维修措施的保修费用对比

保修期内,若对各个部件不采取预防性维修措施,仅在故障后进行修复性最小维修,则各个部件在二维保修期内的保修费用可分别求出,将其与采取预防性维修措施的最优保修费用进行对比,结果如表4所示。

表4 有无预防性维修措施的保修费用对比

通过表4可知,在保修期内采取预防性维修措施后,部件1与部件2的保修费用都有了明显降低,其中部件1的保修费用降低最为明显,降幅高达75.03%,部件3加入预防性维修措施后保修费用有所提高。但总体来看,保修期内该动力装置的保修费用降低了63.31%,这表明预防性维修可以降低保修期内的故障发生的概率,极大地削减保修费用。

4.3 组合维修前后保修费用对比

按照第3.3节中的模型对多部件预防性维修工作进行组合,并计算组合后保修费用。将组合前后的保修费用进行对比,如果严格执行各部件的预防性维修计划,那么在保修期内串联多部件系统保修总费用为6.44万元。按照提出的组合优化方法对各单部件的预防性维修工作进行组合,串联多部件系统的保修费用为5.9万元,费用比优化之前降低8.37%,表明该组合优化方法可以降低该动力装置的保修费用。

根据第3.3节中的模型可知,与优化前相比,各单部件的预防性维修不再是周期性的,转而以基准预防性维修间隔期的整数倍执行,在使用时间维度上,系统共执行7次预防性维修。在使用程度维度上,系统共进行2次预防性维修。在不同使用率下,单部件执行预防性维修的时刻和使用程度如表5和表6所示,表中“+”表示执行预防性维修,“-”表示不执行预防性维修。

表5 各部件预防性维修时刻

表6 各部件预防性维修使用度

各部件的预防维修工作进行组合后,当各部件的实际使用率小于等于0时,保修期的截止期限先在日历时间维度到达。当部件1的使用率小于等于5×10公里年时,需要在日历时间维度上进行7次不完美预防性维修;当部件2的使用率小于等于107×10公里年时,需要在时间维度上进行2次不完美预防性维修;部件3的使用率小于等于1×10公里年时,需要在时间维度上进行1次不完美预防性维修。其中,在4与7时刻,即16年与28年时,3个部件需要共同进行预防性维修。

由表6可知,各部件的预防维修工作进行组合后,当各部件的实际使用率大于0时,保修期的截止期限先在使用程度维度到达。具体来说,当部件1的使用率大于5×10公里年时,需要在使用程度维度进行1次不完美预防性维修;当部件2的使用率大于107×10公里年时,需要在使用程度维度进行1次不完美预防性维修;当部件3的使用率大于1×10公里年时,需要在使用程度维度进行2次不完美预防性维修。当装备使用程度达到时,即动力装置的使用程度达到15×10公里时,3个部件需要共同进行预防性维修。通过表6和表7可以看出,依据不同的使用率,各部件在时间维度或使用度维度按一定间隔执行预防性维修工作,表明该优化方法可为制定动力装置组合维修方案提供参考依据。

5 结 论

本文研究了复杂二维保修装备的组合维修策略,针对包含串联多部件系统的复杂装备,以保修期内保修费用最低为目标,在单部件二维预防性维修费用模型的基础上,引入预防性维修基准间隔期,通过调整各单部件的预防性维修时刻,将各单部件的预防性维修工作进行组合,建立了串联多部件系统二维预防性组合维修费用模型。以某新型防空导弹武器系统导弹发射车动力装置为例进行分析,结果表明,采取组合维修策略后该动力装置的二维保修费用明显降低,充分验证了组合维修策略的有效性。本文建立的预防性维修组合优化模型可为复杂装备的二维保修方案制定提供理论和技术支持。考虑到部队对于装备可用度要求较高,下一步需要对具有经济相关性的复杂二维保修装备进行可用度优化研究。