基于新最速下降算法的自适应波束形成

王 帅, 向建军, 彭 芳, 唐书娟, 李志军

(空军工程大学航空工程学院, 陕西 西安 710038)

0 引 言

阵列天线相较于传统单天线具有空间分辨率高、探测距离远、抗干扰等优点，目前被广泛应用于雷达、声呐、无线通信、空间遥测等领域。例如：在相控阵雷达探测领域，阵列信号处理的应用能够增强目标信号，抑制干扰信号，提高空间探测的分辨率；在阵列麦克风领域中，对语音信号进行增强，从噪声中提取清晰的语音信号，提高话音质量；在无线通信领域中，提高能量和信道的利用率，提升谱效率；在水下声呐探测领域中，对目标进行识别、跟踪和定位，滤除噪声影响，提高检测效率。

波束形成又称空域滤波，能够控制阵列天线收发波束的空间指向，是阵列信号处理的代表性技术之一。波束形成通过对阵列天线各阵元施加不同的复数权值，令各信号之间相互干涉，使得阵列天线输出的信号在目标方向形成主瓣波束，在干扰方向形成尽可能低的零陷来抑制干扰信号的影响，同时尽量降低旁瓣电平来减小杂波的影响。

自适应波束形成是波束形成技术的一种，可以根据目标和干扰的方向，以特定自适应准则自动调节波束指向及零陷，在目标探测和干扰对抗方面发挥了重要作用，具有重大的研究价值和实际意义。经典的自适应波束形成算法包括以下几种：基于最小均方(least mean square，LMS)算法的自适应波束形成，该算法基于LMS误差准则，应用该准则构建目标函数，通过梯度下降法求解目标函数的最优解，用最优解进行波束形成。基于递归最小二乘(recursive least square， RLS)算法的自适应波束形成遵从LMS误差准则，该算法采用递归的方式代替矩阵求逆，相较于通过矩阵求逆的运算方式求维纳解，降低了算法的运算量。最小方差无畸变响应(minimum variance distortionless response, MVDR)波束形成算法基于最大信干噪比(signal to interference plus noise ratio, SINR)准则。该准则使波束形成器输出的干扰加噪声功率与信号功率之比最大来求解波束形成器的最优复权系数，因此一般情况下又被看作是最优波束形成。

1 自适应波束形成的原理

自适应算法可以根据背景环境以一定的准则自动调节阵元的权值。有很多准则可以用来调节权值,波束形成里常用的准则有4种,分别是LMS准则、SINR准则、最大似然比准则和最小噪声方差准则。

最常用的自适应算法是LMS算法,LMS算法因为结构简单、容易实现、计算量小等优点被广泛应用于各种领域,如自适应噪声对消、自适应信道均衡、自适应波束形成等。

其中,基于LMS算法的自适应波束形成采用的是LMS准则,其算法结构如图1所示。

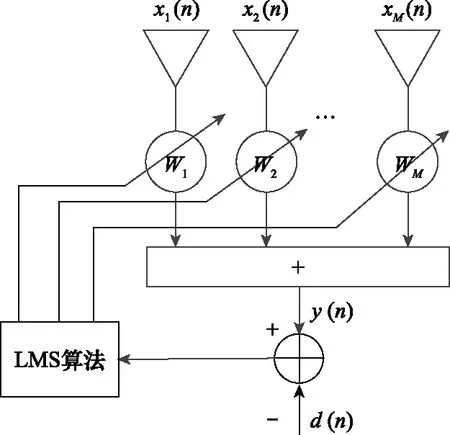
图1 LMS自适应波束形成算法结构图Fig.1 LMS adaptive beamforming algorithm structure diagram

图1中，()代表输入信号,()代表输出信号,()代表期望信号,LMS准则就是通过调节各个阵元的权矢量使阵列输出信号与期望信号的均方误差达到最小。

梯度下降算法的权向量迭代公式如下:

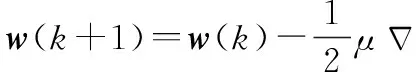
(1)

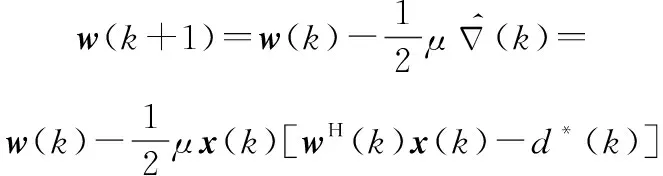
(2)

由于LMS算法具有收敛速度慢,且迭代步长的选择不灵活的缺点,本文引用文献[31]提出的一种改进的LMS算法。文献[31]所提出的算法使迭代步长基于对数函数进行变化,改善了经典LMS算法收敛速度慢且步长固定的缺点,基于对数函数变步长的方式也使得该方法的计算复杂度变大了,没有LMS那么简单易实现,同时还引入了参数和参数,这两个参数的选择需要依靠经验,使得该方法在应用时更加复杂。

改进LMS算法的迭代步长的更新公式如下所示:

()=lg(|()(-1)|)=lg[|(()()-())· ((-1)(-1)-(-1))|]

(3)

式中:参数和参数控制着曲线的形状和整体数值的大小。

将式(3)代入式(2)的迭代公式中，得到基于改进的LMS算法波束形成迭代公式:

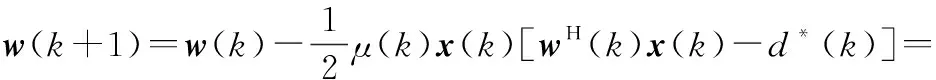
(4)

2 新最速下降波束形成算法的推导

2.1 新最速下降算法

本文提出一种最速下降算法,这种新最速下降算法将高维二次凸优化问题降解到二维上,利用抛物线性质采用循环迭代求解的方式求得高维凸优化问题的最优解。即该方法首先将多元二次凸函数降解为一元二次函数,一元二次函数是一条抛物线,利用抛物线的性质求出抛物线的极值点,通过循环迭代的方式使每次迭代求出的极值点向多元二次凸函数的极值点逼近,最终使结果收敛到多元二次凸函数的极值点。

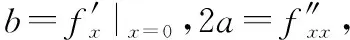
详细的推导过程如下:

假设多元二次函数的一般形式为

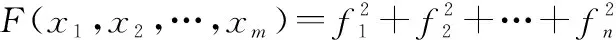
(5)

式中:

=++…+1+=++…+2+⋮=1+2+…++

一般形式中代表函数中自变量的个数,代表约束方程的数量。可以通过本文提出的新最速下降算法来求取函数的极值,新最速下降算法的迭代过程如下所示:

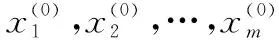
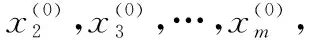
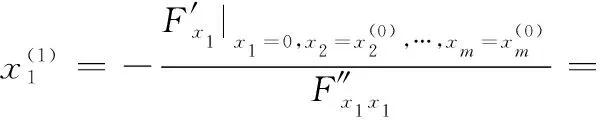
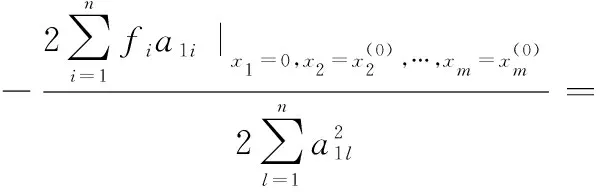
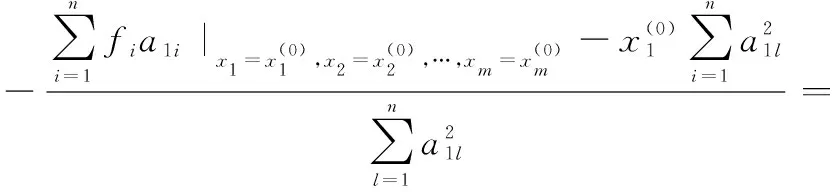
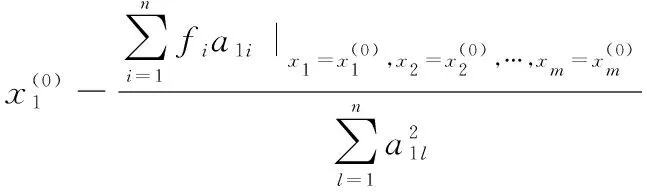
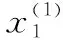
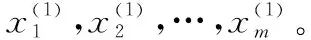
将步骤4中求出的极值点赋值给各个变量,进行循环求取各个变量的极值点,随着迭代次数的增多,各个变量的极值点将越来越逼近于多元函数的极值点。

最终得到的迭代公式如下所示:

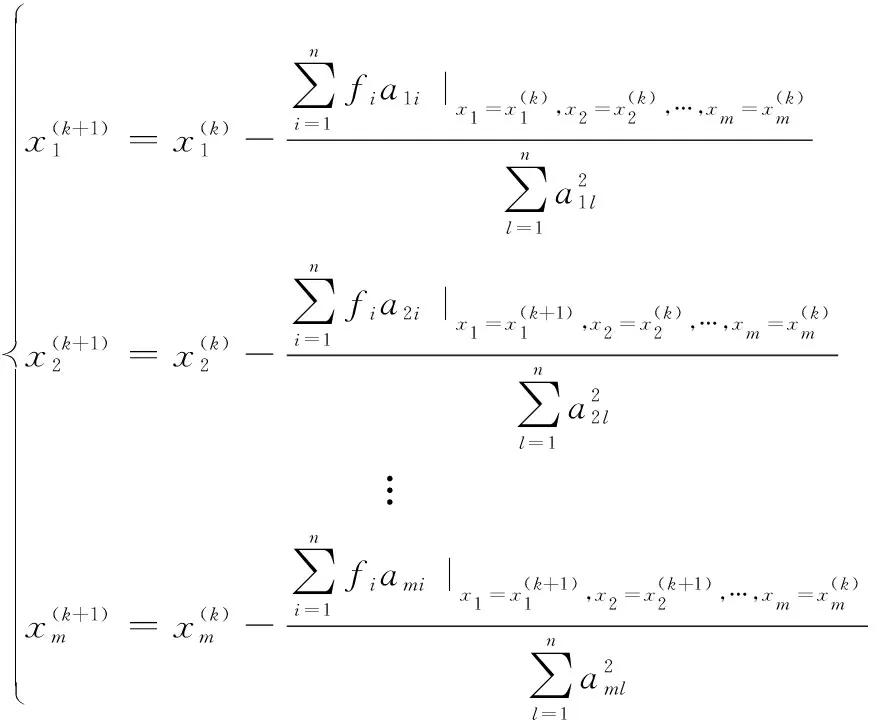
(6)

2.2 基于新最速下降的自适应波束形成算法

本文提出的自适应波束形成算法基于LMS准则,LMS准则是指选取合适的阵列权系数使输出信号与期望信号之间的均方误差最小。

阵列输出信号与期望信号之间的均方误差函数如下:

()=E[|()()-()|]=

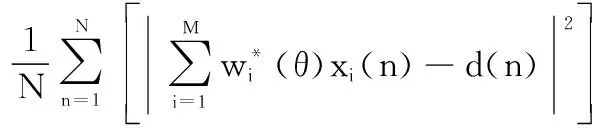
(7)

式中：()代表施加在阵列上的权系数向量；E[·]代表求平均；|·|代表取模。

可以看出均方误差函数即式(7)符合多元二次函数的一般形式,所以可以采用本文所提出的新最速下降算法求解均方误差函数的极值点。

对式(7)求一阶导数和二阶导数得

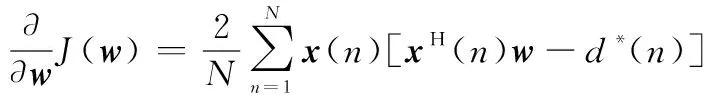
(8)

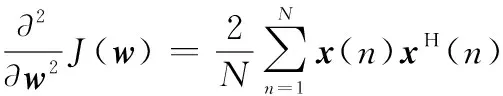
(9)

令

()=()-()

(10)

将式(8)～式(10)的结果代入到式(6)中可以得到权系数的迭代公式:

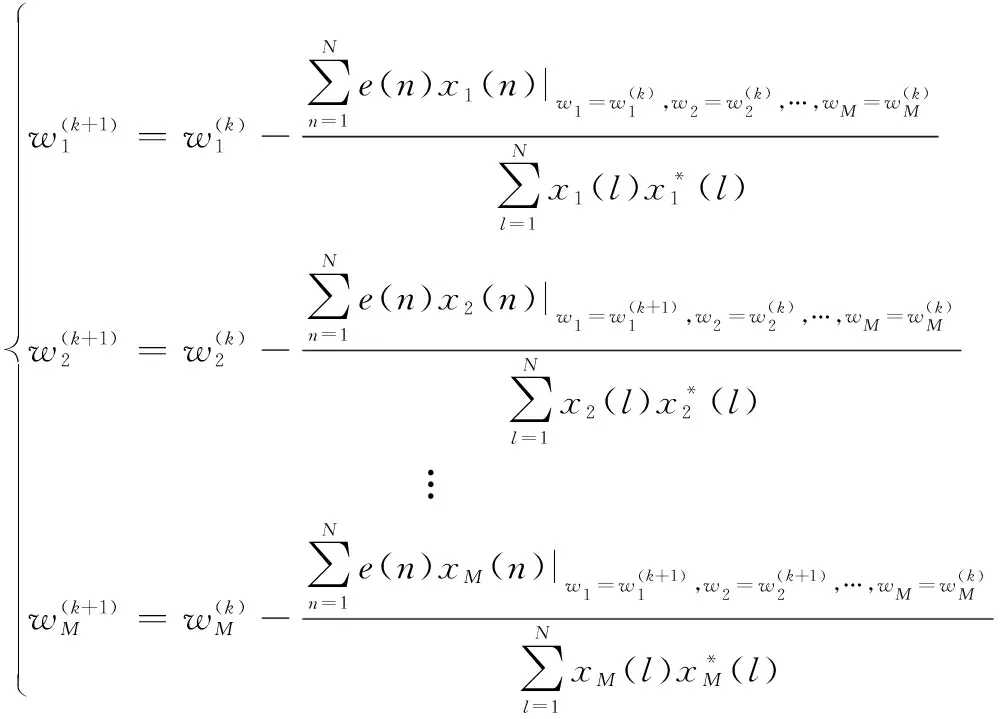
(11)

综上,本文所提出的自适应波束形成算法的步骤可以概括如下：

设定约束方程的数量,对权系数随机赋予初值。

采用式(11)对各个权系数变量进行迭代计算。

进行完一次迭代运算之后,根据约束方程数量对迭代方程中的系数进行更新，即对期望信号和输入信号进行更新,即将期望信号和输入信号以约束方程数量为一组在所有快拍信号中向后滑动一位,即由之前的()(=-+1,-+2,…,)和()(=-+1,-+2,…,)更新为()(=-+2,-+3,…,+1)和()(=-+2,-+3,…,+1)。

使用更新之后的系数重新进行下一次的迭代运算,即重新进行步骤2。

循环执行步骤2～步骤4,直到进行到最后一个快拍的数据,保存最后计算所得的权系数()(代表快拍数)。

用()对阵列进行加权,阵列的波束形成效果达到最佳。

算法的流程图如图2所示。

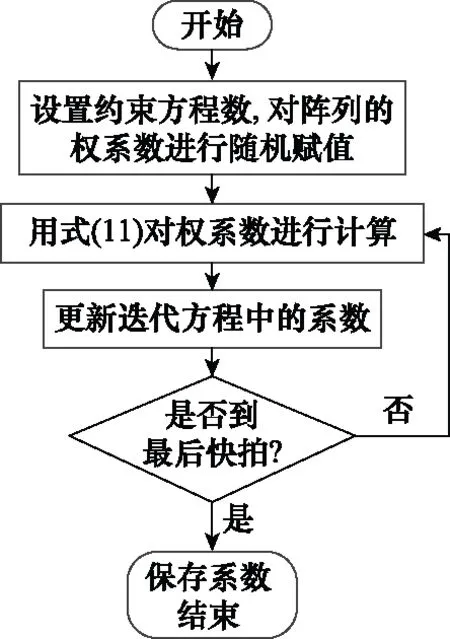
图2 算法流程图Fig.2 Algorithm flow chart

3 仿真分析

使用Matlab软件对波束形成进行仿真模拟,仿真的场景如下:天线阵列是阵元数为16的均匀线阵,干扰的样式采用压制性宽带噪声干扰,目标信号采用脉宽为10 μs、带宽为30 MHz、中心频率为50 MHz的线性调频脉冲信号。在该场景下对算法性能进行仿真分析,主要分析的内容如下:新算法相对于经典LMS算法以及文献[18]中所提到的步长可变、收敛速度更快的改进LMS算法的收敛性的快慢、抗干扰能力的强弱、对样本数的要求等。

3.1 收敛速度对比

仿真环境设置如下:目标方向设置为0°,干扰方向设置为50°,令信噪比(signal to noise ratio, SNR)为0 dB、干噪比(interference to noise ratio, INR)为20 dB、快拍数=600、进行500次蒙特卡罗仿真、LMS算法的迭代步长设置为在可以保证算法收敛的情况下使算法收敛速度最快的最大允许迭代步长,改进LMS算法中的=1 200,=0000 01,所提算法中的约束方程的数量=5,最终得到阵列输出信号与期望信号之间的均方误差与快拍数之间的关系,如图3所示。

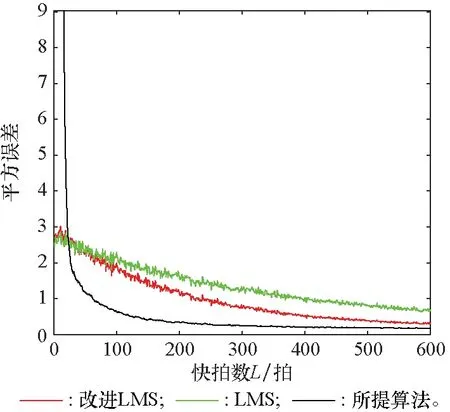
图3 3种算法收敛速度对比Fig.3 Convergence speed comparison of three algorithms

从图3中可以看出,随着快拍数的增多,所提算法最先收敛到最小,改进的LMS算法其次,最后是LMS算法,这说明所提算法的收敛性相较于其他两种算法更快,在进行波束形成时实时性会更好。

3.2 抗干扰能力对比

由于改进LMS算法的性能要优于经典LMS算法,所以以下分析将只与改进LMS算法作对比。令改进LMS算法的仿真环境中INR分别为10 dB、30 dB、50 dB和70 dB,令新算法的仿真环境中INR分别为50 dB、70 dB、100 dB和150 dB,其他条件均与第3.1节的环境保持一致,得到波束指向图如图4和图5所示。

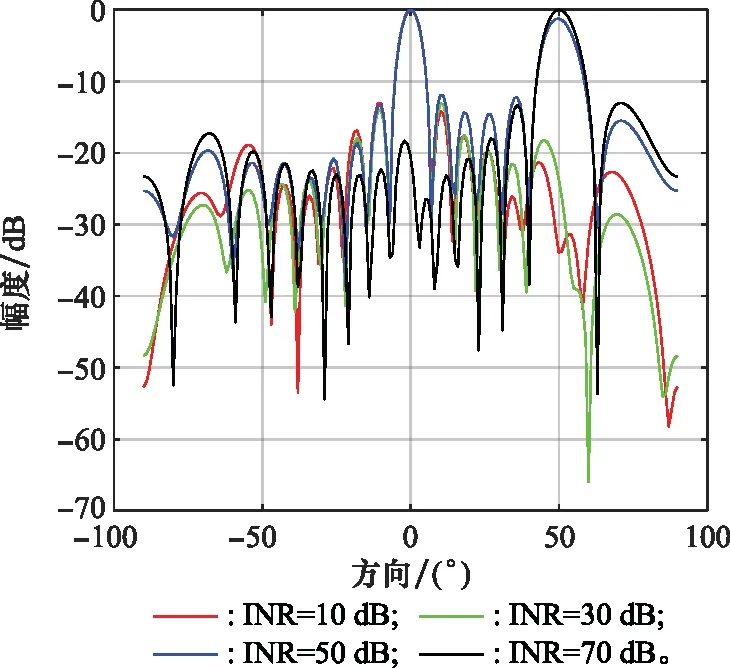
图4 改进LMS算法抗干扰能力的波束指向图Fig.4 Beam pattern of improved LMS algorithm anti-jamming ability

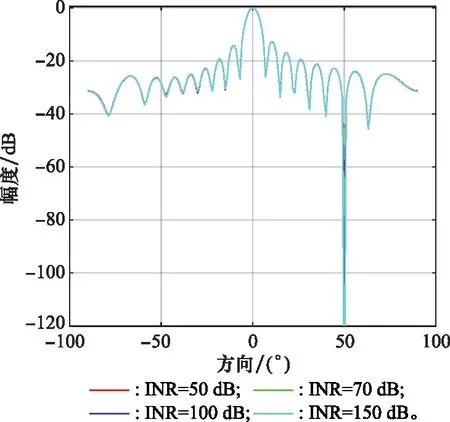
图5 所提算法抗干扰能力的波束指向图Fig.5 Beam pattern of the proposed algorithm anti-jamming ability

从图4中可以看出,当INR=10 dB时,改进LMS算法可以在目标方向形成主波束,在干扰方向处形成凹陷;当INR=30 dB时,改进LMS算法仍然可以在目标方向形成主波束,但是已经无法在干扰方向形成凹陷;当INR=50 dB时,在目标方向形成主波束,但是在干扰方向形成的波束的幅度也接近主波束的幅度,这种情况会大大降低波束形成算法的精度甚至导致无法工作;当INR=70 dB时,在干扰方向形成主波束,在目标方向已经无法形成主波束,此时的波束形成算法已经无法正常工作。

从图5中可以看出,随着INR的增大,所提算法的主波束指向一直保持不变,始终指向目标的方向,在干扰的方向始终会形成零陷,而且随着干扰的增强零陷也会越来越深,对干扰的衰减越来越大，从而消除干扰的影响。

通过图4和图5的对比,可以看出所提算法在抗干扰方面有很大优势。即使INR达到150 dB,所提算法仍然可以正常工作,在目标方向形成主波束,在干扰方向形成深度凹陷。

3.3 抗噪声能力对比

将改进LMS算法的仿真环境设置为INR=20 dB,快拍数=600,SNR分别设置为0 dB、-10 dB、-20 dB、-30 dB;将所提算法的仿真环境设置为INR=50 dB,快拍数=600,SNR分别设置为0 dB、-20 dB、-40 dB、-60 dB;其他设置均与第3.1节一致,得到波束指向图如图6和图7所示。

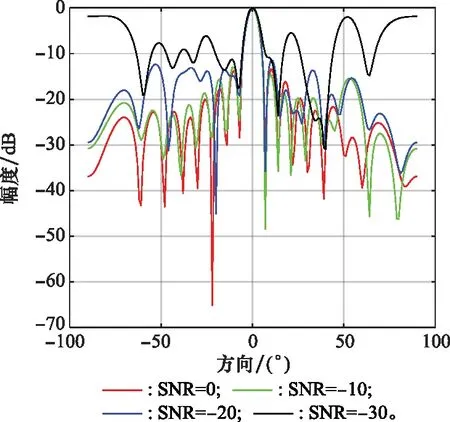
图6 改进LMS算法抗噪声能力的波束指向图Fig.6 Beam pattern of improved LMS algorithm anti-noise ability

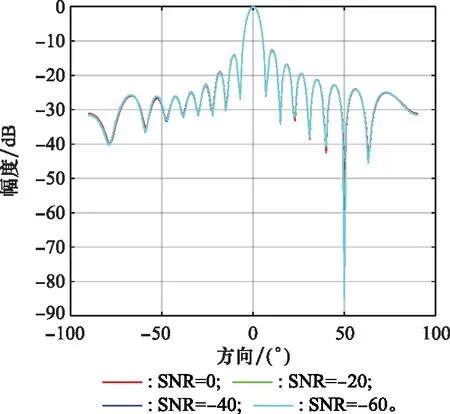
图7 所提算法抗噪声能力的波束指向图Fig.7 Beam pattern of the proposed algorithm anti-noise ability

图6是改进LMS算法在SNR分别为0 dB、-10 dB、-20 dB、-30 dB情况下所得到的波束指向图。从图6中可以看出，当SNR为0 dB时,可以在干扰的方向形成凹陷,在信号方向形成主瓣;当SNR为-10 dB和-20 dB时可以在信号方向形成主瓣,但是无法在干扰方向形成凹陷;当信噪比为-30 dB时波束指向图严重失真,已经无法正常工作。

图7是新算法在SNR分别为0 dB、-20 dB、-40 dB、-60 dB情况下所得到的波束指向图。从图7中可以看出,即使SNR下降到-60 dB时,所提算法仍然可以在干扰的方向形成凹陷,在信号的方向形成主瓣,可以保持正常工作。

综上,经过对比可以得到结论,所提算法的抗噪声能力比改进LMS算法要好。

3.4 低快拍数下的性能对比

将改进LMS算法的仿真环境设置为INR=20 dB,快拍数分别设置为100、50、30、10;将所提算法的仿真环境设置为INR=50 dB,快拍数分别设置为100、50、30、10;其他设置均与第3.1节一致,得到波束指向图如图8和图9所示。

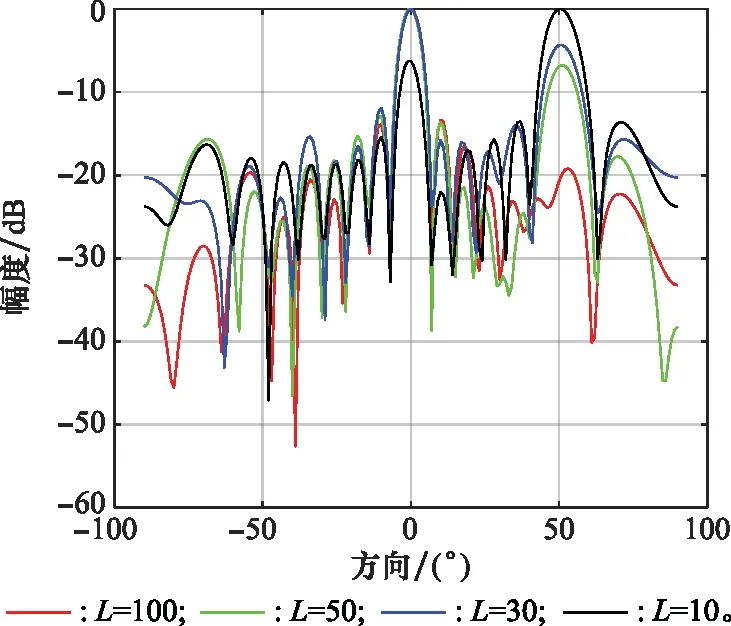
图8 改进LMS算法低快拍下的波束指向图Fig.8 Beam pattern of improved LMS algorithm under low snapshot

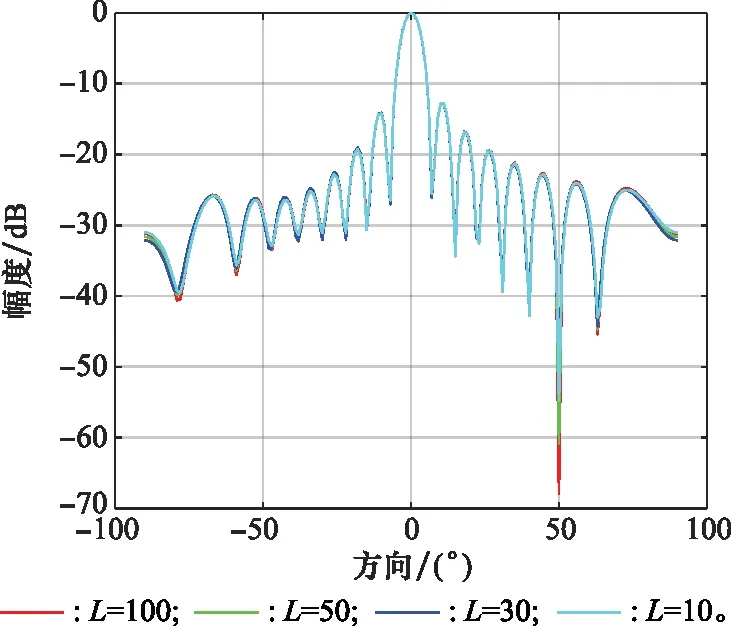
图9 所提算法低快拍下的波束指向图Fig.9 Beam pattern of the proposed algorithm under low snapshot

从图8中可以看出,改进LMS算法在快拍数较少时已经无法在干扰的方向形成凹陷,在快拍数为100、50的时候虽然无法在干扰方向形成凹陷,但是勉强可以在信号方向形成主瓣,在快拍数降到30以下时,改进LMS自适应波束形成无法正常工作。可见改进LMS算法在低快拍的情况下性能不是很好。

从图9中可以看出,即使是在快拍数很少的情况下,新算法仍然可以在目标方向形成主波束,在干扰方向形成凹陷,实现正常的波束形成并抑制干扰。所以所提算法具有可以在低快拍情况下工作的优点。

3.5 所提算法的抗干扰性能分析

为了对所提算法的抗干扰性能进行分析,引入干信比(interference-to-signal ratio, ISR)作为衡量指标,ISR即干扰功率与噪声功率的比值。为了直观地对比干扰和信号的关系,将仿真环境中噪声功率设置为0,快拍数设置为600,波束形成器输入的ISR设置为0～200,经所提算法波束形成后得到输出ISR与输入ISR的关系,如图10所示。

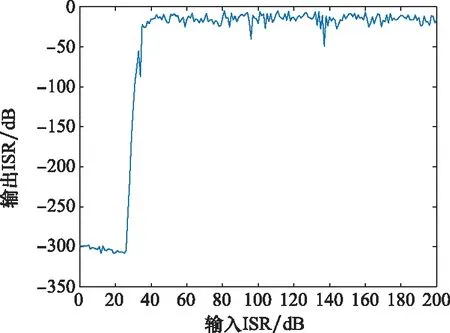
图10 输出ISR与输入ISR的关系Fig.10 Relationship between output ISR and input ISR

从图10中可以看出,当输入ISR小于30 dB时,所提算法对输出ISR具有较大的改善,大约能够达到300 dB。输入ISR由30 dB转向40 dB时,所提算法对输出ISR的改善会急剧恶化,当输入ISR为40 dB时,对输出ISR的改善约为40 dB。当输入ISR大于40 dB时,输出ISR始终维持在0 dB左右,随着输入ISR的增大,对输出ISR的改善逐渐增大,但是改善效果不如输入ISR小于40 dB的阶段。综上,所提算法对干扰的抑制能力在输入ISR小于40 dB时较强,当ISR大于40 dB时虽然仍然具有一定的抑制能力,但是抑制能力会有一定程度的下降。

接下来分析抗干扰性能与干扰信号数量的关系,将输入ISR设置为30 dB,分别在不同方向施加1～16个相互独立的干扰信号,得到输出ISR，如图11所示。

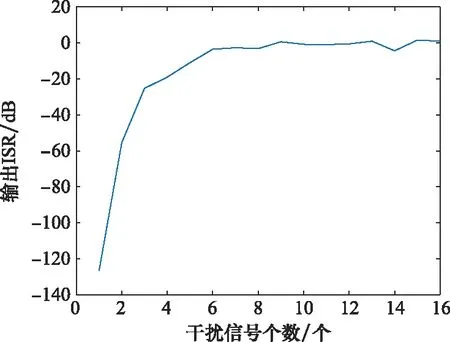
图11 输出ISR与干扰数量的关系Fig.11 Relationship between output ISR and the number of interference

从图11中可以看出,当干扰源的数量少于6个时,随着干扰源数量的增加,算法对输出ISR的改善作用逐渐减弱。当干扰源的数量大于6个时,输出ISR逐渐趋近于0 dB,达到算法的极限。所以当干扰源的数量较少,少于6个时,算法的抗干扰性能较强,当干扰源数量较多时,虽然算法对干扰仍有一定抑制能力,但是效果会变差。

图12为干扰源数量分别为1、5、9、13时的波束指向图,可以看到随着干扰源数量的增加,在干扰方向形成的凹陷减小,即对干扰的抑制能力减弱。当干扰的数量大于6时,波束图的旁瓣升高,在干扰方向的抑制能力减弱较为明显,波束形成的性能变差。

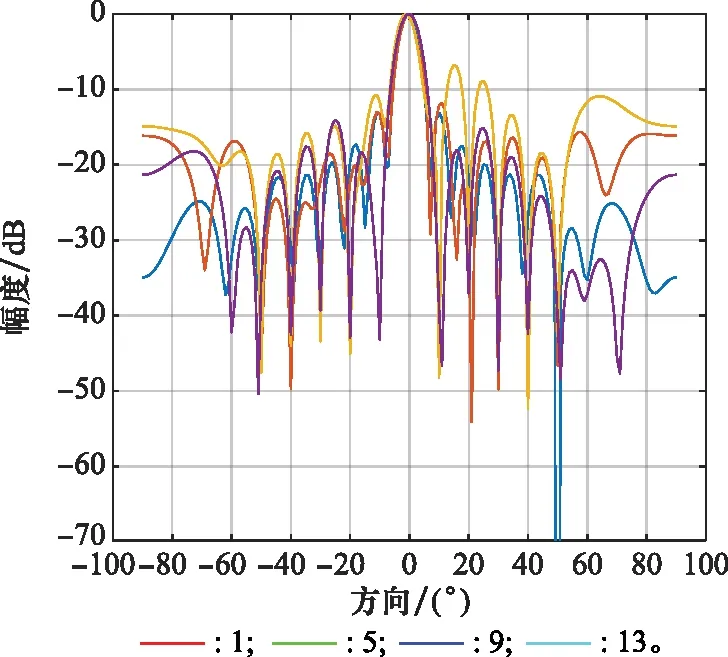
图12 干扰数量不同时波束图对比Fig.12 Comparison of beam patterns with different interference numbers

4 结 论

经过仿真分析可以看出，所提出的最速下降算法具有收敛速度快、结果更精确的优点。将该算法用于自适应波束形成,得到基于新最速下降法的自适应波束形成算法，该算法具有以下特点:收敛速度更快,具有更好的实时性;可以对抗强干扰,即使干扰的强度很高,算法都可以在干扰方向形成衰减,在目标方向形成主瓣,保证正常工作;在低快拍数的情况下算法仍然可以正常工作,在干扰方向形成衰减,在目标方向形成主瓣。