虚拟波束四阶累积量DOA估计方法
2022-06-25刘甲磊马佳智施龙飞
刘甲磊, 马佳智, 施龙飞
(国防科技大学电子科学学院, 湖南 长沙 410073)
0 引 言
信号波达方向估计(direction of arrival,DOA)是阵列信号处理的重要研究内容,广泛应用于雷达、通信、声呐、无源定位等各个领域[1-2]。最具代表性的子空间多重信号分类(multiple signal classification,MUSIC)及衍生的多种算法[3-4],构成了阵列信号DOA领域的广泛应用基础,但其本质为基于信号二阶统计特性构建的谱估计算法。相较信号二阶统计特性,信号四阶统计特性因其对任何形式的高斯过程的不敏感性,可以最大程度地抑制高斯噪声的突出优点,使其在盲源分离和DOA估计上获得许多开拓性的研究[5-7]。并且由四阶累积量(fourth-order cumulant,FOC)计算性质,Liu等[8]证明了其在扩展阵列孔径和阵列校准的有效性。陈建等[9-10]提出的基于FOC的MUSIC-like阵列扩展方法,应用阵列接收信号的全FOC构建扩展阵列,进行多源信号DOA估计,可有效提高阵列分辨率。文献[11-12]分别提出了期望最大化(expectation maximization,EM)算法迭代和相关源信号下,利用信号FOC进行DOA估计的方法。齐栋等[13]提出了基于FOC的高斯色噪声下二维DOA估计方法。Zhang等[14]提出了高斯色噪声下基于FOC的无网格相干DOA估计方法,表现了FOC算法在高斯色噪声背景下的有效性。Xue等[15]将FOC用于均匀圆阵DOA估计,获得较好的估计精度。文献[16-17]提出了一种对MUSIC-like算法去冗余的FOC的DOA方法,只利用部分无冗余的FOC切片构建FOC矩阵,矩阵阶数大大下降,利于工程化实现。但是其构建的去冗余FOC矩阵,破坏了原有矩阵的对称性,DOA估计精度有所下降,Shi等[18]提出了一种构建Toeplitz去冗余FOC阵的方法。但由于FOC对野值非常敏感,真实情况阵列误差未知且未被校准时,估计性能下降十分严重。文献[19-21]分别建立阵列幅相和互耦误差下基于FOC的DOA估计模型,但每种方法只能部分消除一种误差来源,较实际多误差因素耦合时并未提及。
针对阵列雷达实际面临复杂电磁环境,在强干扰场景和阵列误差并存时,低信噪比(signal to noise ratio, SNR)目标信号DOA难估计的问题,本文提出了一种基于虚拟波束FOC(virtual beam forming-FOC,VBF-FOC)的DOA估计算法。算法通过阵列接收信号主成分提取构建初始虚拟波束,再利用参数化的方向波束高斯窗对初始波束进行修正,可比较有效提取强干扰下弱目标信号分量,一定程度减小阵列误差对接收信号失真影响,降低SNR目标的估计损失。利用以上两步形成新的联合导向矢量,与FOC分解的噪声子空间进行空间谱计算,可得到精确DOA估计。本文建立了算法流程框架,并推导该算法虚拟波束形成及其谱估计的公式,在非等功率信源场景下验证了算法有效性。仿真对比了基于阵列信号全FOC的DOA估计的MUSIC-like算法,对MUSIC-like中FOC去冗余的简化算法(reduced FOC,ReFOC),以及利用本文方法进行虚拟波束处理后的VBF-FOC和VBF-ReFOC两种方法。仿真结果表明,虚拟波束处理后的VBF-FOC和VBF-ReFOC两种方法,信号DOA检测率和估计精度都有明显提升,对于强干扰背景下的低SNR目标,表现出更强的适应性和鲁棒性。
1 算法原理
论文虚拟波束形成含义是,对阵列单脉冲接收信号进行阵元级加权,利用合成波束信号作为输入进行空间谱估计,算法模拟了阵列波束形成空间扫描的过程,构建本不存在的波束进行DOA估计,故为虚拟波束。VBF-FOC算法首先对阵列接收信号进行归一化的虚拟波束域提取,将N路输入提取为K(K≤N)路初始虚拟波束并对其中主要信号分量的进行DOA粗估计,计算DOA粗估计下主波束的方向性高斯修正窗函数,利用修正高斯窗与初始虚拟波束相乘,得到修正后的虚拟波束。将主波束信号代替阵列接收信号计算FOC矩阵,进而分解出FOC下的信号子空间和噪声子空间,联合上步计算得到的高斯窗修正的波束方向矢量,进行FOC谱估计,搜索谱峰从而得到信号的精确DOA估计。算法流程框图如图1所示,各步原理及分析下文一一叙述。
1.1 信号模型
以N元均匀等距线阵模型,阵元间距为d,雷达发射信号波长为λ,阵列波束指向为θ0。远场空间存在M(M≤N)个入射角度为θm(i=1,2,…,M)的窄带信源sm(t),其中目标信号位于θ1,剩余M-1个为干扰信源。则理想情况下,阵元接收信号为
X(t)=AS(t)+Vn(t)
(1)
式中:Vn(t)∈N(0,σ2)为高斯白噪声矩阵;S(t)=[s1(t),s2(t),…,sM(t)]为信源的时域信息矩阵;[A=a(θ1),A=a(θ2),…,A=a(θM)]为阵列流形矩阵,a(θM)=[1,e-jφm,…,e-j(N-1)φm,]表示其中各分量,φm=(2πdsinθm)/λ为阵元间相移因子。
但实际应用,阵列误差对信号观测的影响不可忽略。阵列误差来源分别为阵列幅相误差、互耦误差、空间位置扰动误差3部分,且通常同时存在且伴随观测始终。为更真实模拟多源非理想特性场景,下面对3种误差因素与信号观测影响进行分析。
阵元通道幅相特性不一致是造成阵列幅相误差的主要原因,各阵元通道幅相特性不一致时,其幅相误差因子矩阵为
Γ=diag[ρ1ejφ1,ρ2ejφ2,…,ρNejφN]
(2)
式中:ρn表示第n(1≤n≤N)个阵元的幅度增益;φn表示第n个阵元的相位误差。
工程应用中各阵元间的耦合效应产生的误差为互耦误差,互耦矩阵在通常情况下为对称Toeplitz矩阵。其形式为

(3)
式中:cm,n为第m个与第n个阵元间的幅度互耦因子;γm,n为第m个与第n个阵元之间的相位互耦因子。由互易定理,cm,n=cn,m,γm,n=γn,m,由于随着阵元间距的增大,互耦效应快速减弱,通常可将C建模为部分为0的稀疏矩阵。
N元阵列M个窄带信号下,阵元n的位置扰动为(Δxn,Δyn,Δzn),c为光速,则第m个信源在阵元n上的延时扰动为
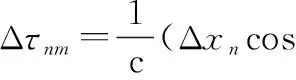
(4)
此时空间扰动误差矩阵为
W=[w(θ1),w(θ2),…,w(θM)],w(θm)=[e-jw0Δτ1m,e-jw0Δτ2m,…,e-jw0ΔτNm]T
(5)
相似的,当3种误差因素并存时,阵列的导向矢量及阵列流形可以表示为
(6)
(7)
此时真实信号接收模型为
(8)
1.2 VBF-FOC算法
1.2.1 FOC子空间分解
假设独立信源发出的信号为零均值、非高斯的信号,则复信号阵列输出的FOC矩阵为
(9)
式中:∀k1,k2,k3,k4∈{1,2,…,N}。
根据式(9),定义阵列误差影响下的FOC切片的展开式为
(10)
式中:将不同来波角度方向源信号FOC矩阵的简记为
(11)
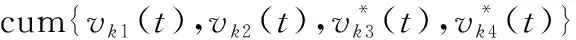
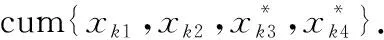
(12)
(13)
实际应用中,由于不同源信号来自于不同系统,可认为各信源间相互独立,则源信号FOC矩阵CS的一个切片为
(14)
进一步可得,CS中仅有M个元素不为零,且非零元素均位于CS的对角线上。将CS的对角线特征值按大小重排后,可得新形式为
(15)
(16)
式(15)为阵列信号FOC矩阵CX的特征分解形式,式(16)为分解特征矩阵。其中,ΛM为M个大特征值(信源)所对应的特征值矩阵,ON2-M为N2-M个小特征值(噪声)所对应的特征值矩阵,B=[b(θ1),b(θ2),…,b(θN2)]为分解得到的特征向量构成的矩阵,可理解为FOC形成虚拟阵列的导向矢量矩阵,其中对应方向θ的导向矢量为
(17)
式中:⊗表示Kronecker积。相应可得到信号子空间ES和噪声子空间EN为
ES=span{b(θ1),b(θ2),…,b(θM)}
(18)
EN=span{b(θM+1),b(θM+2),…,b(θN2)}
(19)
则基于FOC直接分解的空间谱为
(20)
1.2.2 虚拟波束FOC计算
FOC作为信号的四阶统计特性,其高阶的计算过程决定了其对于数据野值很敏感。当场景中存在多个非等功率源信源,信号强度差异大时,SNR大的信源,其四阶统计特性会远强于小SNR信源,这就造成了复杂场景下低SNR目标DOA估计的困难。
虚拟波束形成,是对阵列接收信号X中各阵元信号进行加权,通过主成分提取方法分离阵列信号X中的主要信息量。实际权系数矩阵求取,是对X的自协方差矩阵进行特征分解,从中选取对应主信号分量的大特征值信号,对各来波方向信号进行粗提取。对各源信号提取时,为提升低SNR目标的DOA估计性能,虚拟波束会对各信号分量进行特征值归一化处理,形成波束的权矩阵。波束的构建方法为
RXX=XXH=UΛUH
(21)
U=[u1,u2,…,uN]
(22)
Λ=diag[λ1,λ2,…λN]
(23)
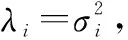
将UH前乘至阵列数据阵X上得P=UHX,计算P的协方差阵为
RPP=[UHX][UHX]H=[UHX][XHU]=UH[UΛUH]U=Λ
(24)
由P的协方差阵为对角阵,可证明P的各行互相正交,且P各行为X特征分解的信号分量,其在P中排序与特征值能量大小顺序相同,其中大特征对应信号分量构成信号主分量空间,谱估计时又叫信号子空间。
为使信号各分量能量相当,通过信号分量特征值归一化的方法,减小强干扰压制下对低SNR目标的混叠影响。取虚拟波束变换阵W=Λ-1/2UH,将其前乘至阵列数据阵X上,得构建波束为
(25)
(26)
同式(24),可证明构建的虚拟波束Z的协方差阵为单位阵,即Z中各行互相正交,且每行数据代表的信号分量能量都为1,通过虚拟波束构建的Z中各行信号为去除了二阶统计相关下的正交信号。
以虚拟波束信号为输入,进行FOC的子空间分解,则由式(13)得Z的FOC矩阵为
(27)
(28)
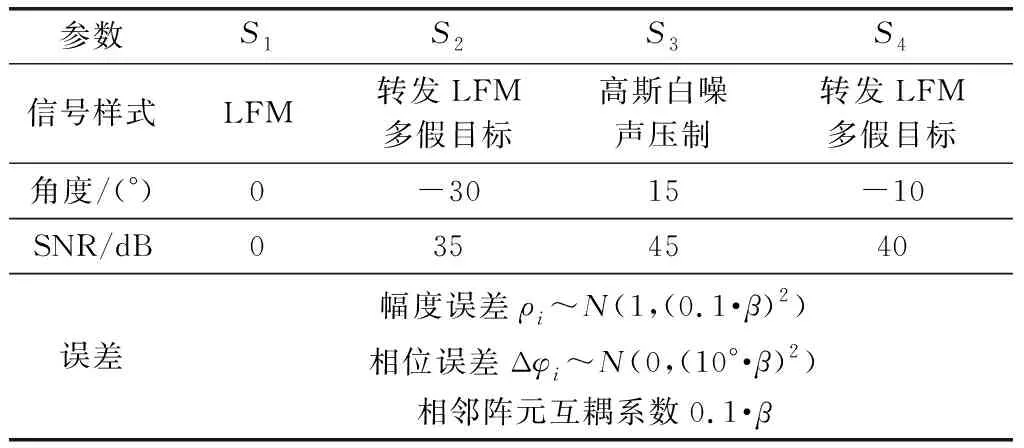
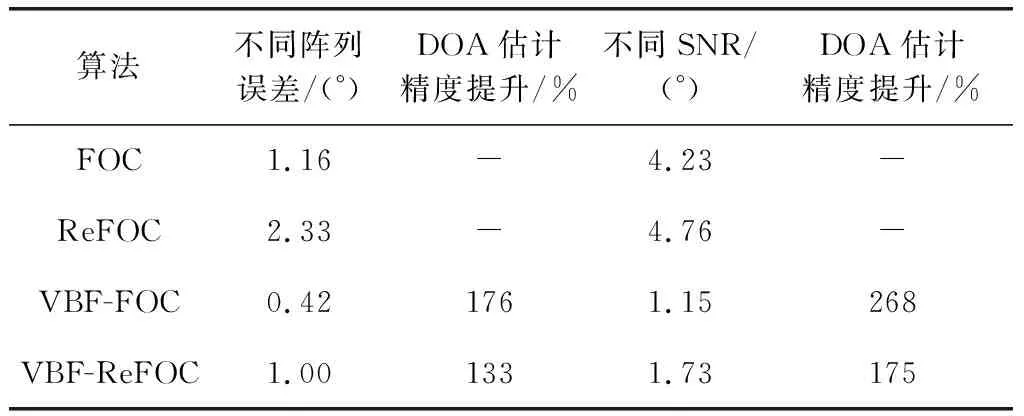
式中:D=[d(θ1),d(θ2),…,d(θK2)]为虚拟波束FOC矩阵特征分解,得到的特征向量构成的矩阵,代表扩展FOC矩阵的方向导向阵;K为提取的虚拟波束个数。当K=N时,Z为同维波束阵;当K 1.2.3 高斯窗修正的虚拟波束FOC谱估计 根据FOC扩展的方向导向阵,可得对应方向θ的导向矢量为 d(θ)=w(θ)⊗w*(θ) (29) (30) 式中:w(θ)定义为虚拟波束方向图矢量,可理解为构建虚拟波束时,各波束对来波方向为θ的信号加权的权值系数。 w(θ)中,当θ遍历角度区间(-90°,90°)取值时,记W(θ)=[w1(θ),w2(θ),…,wK(θ)]T表示各波束的全向方向图矢量,表明构建的虚拟波束对来波信号具有主分量提取的作用,但其并不能完全提取出各单独源信号。残存的其余信号分量,会在构建的主波瓣外,形成小的鼓包,波束畸变会对谱估计时DOA估计性能产生影响。 为消除波束畸变影响,本文在虚拟波束基础上,进一步利用w(θ)中源信号角度的粗估计信息,建立高斯窗来修正虚拟波束的方向图矢量。具体方法为:根据信号子空间中大特征值的前M路信号,求取方向图矢量w1(θ)~wM(θ)的极大值得到DOA粗估计,表示为 (31) (32) 式中:δ为角度高斯分布标准差,δ取值一般为阵列3 dB主瓣宽度的平方根。以阵元数N,阵元间距为半波长时,可取 (33) 相应地,记W中前M路表示大特征值波束权阵记为W1,小特征值波束权阵记为W2。则高斯窗修正后的方向图和阵列导向矢量分别为 (34) (35) 综上,可得在虚拟波束提取和高斯窗修正下的联合谱估计函数为 (36) (37) 为更好说明虚拟波束提取和高斯窗修正方法,对源信号DOA估计的影响,下面以信号处理效果进行分析。 实验场景:均匀线阵阵元数N=10,阵元间距半波长,3 dB主瓣宽度10.2°。空间3个独立点源信号S1~S3方位角分别为:0°,-30°,15°;SNR分别为:0 dB,35 dB,45 dB。其中,S1模拟低SNR的弱目标信号,S2和S3为强干扰信号。S1~S3单位SNR下的信号样式见图2所示。其中,S1为线性调频(linear frequency modulation, LFM)信号,带宽B=5 MHz,脉宽τ=20 μs,采样频率fs=10 MHz,S2为对S1的转发多假目标干扰信号,S3为高斯白压制干扰信号。 计算空间谱函数时,每个角度θ的谱值由阵列导向矢量与噪声子空间的正交关系可得。本文提出虚拟波束形成方法,阵列导向矢量为波束方向图矢量Kronecker积,虚拟波束中主波瓣以外的混叠信号分量,会对谱估计性能产生影响。为进一步提升DOA估计性能,考虑修正信号主分量的波束方向图,使虚拟波束主瓣内权值基本不变、抑制主波瓣外的权值起伏。 为保持各波束的连续性,选用高斯分布窗对波束方向图进行修正。图4所示为利用式(34)高斯窗修正后的归一化波束方向图,可见每个信号波束外的起伏被很好抑制,波束更加纯净。但是,高斯窗修正本质是为避免主瓣外波束起伏对空间谱估计产生影响,对DOA的粗估计结果不会有提升。 定量分析算法高斯窗修正效果其对信号谱估计精度的提升,取式(38)建立的波束误差统计量,表征高斯窗修正前后,所抑制的权值起伏差异量在整个角度区间统计平均的归一化误差比。 (38) 式中:N表示θ遍历角度区间(-90°,90°)区间的离散取值点数;下标序号i表示第i个虚拟波束。 以图2仿真场景为例,进行100次蒙特卡罗仿真,如图5所示。将3个高斯窗修正后波束虚拟波束的误差做归一化,可见高斯窗修正可平均对波瓣起伏均方根误差(root mean square error, RMSE)抑制10%以上。 图6所示为是否使用高斯窗修正,在100次蒙特卡罗仿真中,信号的DOA估计精度误差统计平均。可见,使用高斯窗修正后的信号谱估计精度,较修正前有明显提升,高斯窗修正前算法DOA估计精度为0.27°,修正后为0.06°,统计结果充分表明了高斯窗修正使信号等效导向矢量更加纯净,较大程度避免了信号混叠下对谱估计峰值计算的误差影响。 实验参数设置见表1所示,空间场内共存在4个源信号,其中S1~S3设置同第1.3节不变,新增S4模拟主瓣干扰点源场景。阵列误差由因子β整体控制,因子β越大,阵列误差越大。相邻阵元间互耦系数最大为0.1β,远离依次减弱,5个阵元外互耦效应忽略不计。空间扰动误差为乘性误差,其大小可由幅相误差、互耦误差乘积近似代替,不再单独设置。 表1 参数设置 实验方法为基于阵列信号全FOC的DOA估计的MUSIC-like算法,以及对MUSIC-like中FOC去冗余的简化算法。方便起见,分别记MUSIC-like及其简化算法为FOC和ReFOC算法。其中,ReFOC算法运算更快,但牺牲了部分DOA精度。用本文构建高斯窗修正的虚拟波束进行DOA估计的方法,分别记为VBF-FOC和VBF-ReFOC。 图7所示为误差因子β=1,即幅度、相位和阵元互耦有10%误差时,4种方法的角度估计谱。其中,ReFOC估计精度较差,但经虚拟波束处理后的VBF-ReFOC精度明显提升;且对比FOC和VBF-FOC(红色与蓝色线),0°的S1目标谱峰高度明显改善,表明在波束构建时,利用信号空间特征值归一化,弥补了非等功率信号的影响,有助于提升低SNR目标的DOA估计性能,与理论分析吻合。 DOA谱峰估计时,可能会因角度分辨率不够、对非等功率信号和阵列误差适应性差等因素,造成信号DOA漏检。为考察几种方法极限条件下信号检出性能,设置场内含S1和S4两点源信号,模拟主瓣干扰场景下目标DOA检测性能。若区间内可形成两个谱峰,则目标及干扰信号DOA均可成功估计,DOA检测成功率为100%;若只能检测到一个谱峰,则认为主瓣干扰信号S4淹没目标信号S1,角度分辨率不够致使目标检测失败,DOA检测成功率为50%。图8为β=1,两点源角度间隔在5°~10°变化时,100次蒙特卡罗仿真的信号DOA检测成功率。可见,利用信号全FOC进行估计的FOC方法,不容易产生漏检,且经信号的虚拟波束化后,VBF-FOC、VBF-ReFOC两种方法的目标信号DOA检出成功率,较处理前性能有显著提升。 除DOA的检出性能外,更重要的评估指标是DOA估计精度。图9为表1源信号参数下,阵列误差因子β在0~1.5变化时,100次蒙特卡罗仿真下几种方法DOA估计精度,评价指标选取DOA估计与真值间RMSE。其中,图9(a)为场内4个源信号DOA估计的平均RMSE性能,考察算法DOA估计整体精度;图9(b)为针对低SNR目标S1的DOA估计RMSE,考察算法对强干扰下弱目标DOA估计精度。结果可见,本文提出VBF-FOC算法的整体及对低SNR目标估计精度,都有明显优势;且在虚拟波束处理后,估计RMSE较之前方法都有很大下降。在阵列误差不大于10%的影响下,VBF-FOC算法的源信号估计RMSE可稳定在0.5°以内,表现出对阵列误差和非等功率信号情形下更强的适应性。 图10为表1源信号参数下,弱目标信号SNR在-10~10 dB变化情况下,100次蒙特卡罗仿真的算法估计精度对比。显而易见,文章提出基于VBF处理的两种算法,低SNR目标DOA估计收敛更快。在都利用FOC进行计算的情况下,VBF-FOC在目标信号-6.5 dB时可收敛到1°估计精度,而对应FOC方法SNR需求是3 dB。相较而言,达到相同DOA精度,VBF-FOC对信号SNR的需求可降低平均10 dB,实现低SNR下的目标高精度DOA估计。 表2为两种变化场景下,4种方法计算DOA估计平均精度值。场景1:固定SNR=0 dB,阵列误差因子β在0~1.5变化;场景2:固定阵列误差因子β=1,SNR在-10~10 dB变化。可见,VBF-FOC算法估计精度更高、适应性更强,且对比直接利用阵列接收数据的FOC进行DOA估计的算法,本文提出的VBF处理后算法的DOA估计精度平均可提升150%以上。 表2 不同算法DOA估计平均精度 事实上,为保证虚拟波束方法DOA运算精度,第2.2节讨论时,均采用波束数目K=N(阵元数)的等维波束构建方法。若K 通常对于一个K×K阶矩阵进行特征值分解,其运算复杂性约为O(K3)。而FOC矩阵进行DOA估计时,相当于对原有阵列维数进行扩展,FOC矩阵阶数越高,运算复杂度越大。而本文提出虚拟波束构建,虽然也需特征值分解,但却是基于阵列信号的,对比FOC矩阵可视为低维矩阵。表3所示为100次蒙特卡罗仿真下,4种方法平均运算时间对比。当矩阵阶数都为10时,VBF处理后算法运算时间只同比增加了约0.04 s,基本可忽略不计。 表3 算法运算时间 结合图11分析,在计算精度和运算速度需要做平衡,取VBF=8时,VBF-FOC算法较FOC方法可在波束降维处理下,运算时间减小一半以上的情况下,仍可获得DOA估计精度一倍的提升。 本文提出了一种在构建虚拟波束框架下,利用FOC进行DOA估计的改进算法(VBF-FOC和VBF-ReFOC)。算法通过阵列接收信号主成分提取和方向波束矢量高斯窗修正两步,形成新的联合导向矢量进行DOA空间谱估计。仿真结果表明,本文提出的VBF-FOC算法DOA估计精度最高,VBF-ReFOC精度次之但运算较快,二者在利用虚拟波束形成的处理后,可对源信号DOA估计精度较现有FOC方法提升150%以上,尤其对于场内同时存在多个非等功率源信号时,方法对低SNR目标精度提升更加明显,表现出算法对复杂干扰环境DOA估计更好的适应性和鲁棒性。在运算时间方面,虚拟波束形成对运算复杂度增加可忽略不计,且可通过虚拟波束降维处理,实现较高精度下的快速DOA估计。需要注意的是,本文在理论建模时采用均匀线阵,但是算法主体思想信号主成分提取和高阶累积量特征分解,对于阵列形式约束较小,因此算法对于均匀圆阵等情形也适用。算法验证时,考虑了阵列幅相、互耦等误差因素影响,对工程应用中阵列误差具备一定适应性。但是,考虑FOC的计算复杂性,在雷达等计算资源比较充分的平台,推广应用价值更好。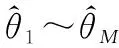
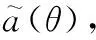
1.3 虚拟波束提取与高斯窗修正效果分析

2 仿真实验
2.1 信号DOA检测性能分析
2.2 DOA估计性能分析
2.3 运算速度分析

3 结 论
