数值计算在求解带电体电势教学中的应用

何 沛 张 鑫

（ 1.铜陵学院，安徽 铜陵 244061 2.池州学院，安徽 池州 247000 ）

一、前言

电势作为电学中最基础的物理量之一， 其求解方法有两种： 一种是根据带电体在空间所产生的电场强度，通过电势的定义，直接积分获得空间任意一点的电势。 若取无穷远处为电势零点，则空间任意点P 的电势为[1]，

由于电场是矢量， 该积分计算需要将电场沿坐标轴进行分解， 将其在各坐标轴上的分量进行积分运算，计算过程比较复杂。

另一种求解电势方法为根据电势叠加原理，将连续带电体分割成很多电荷元，每个电荷元在空间P点产生的电势为[2,3]，

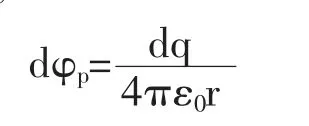
其中r 为电荷元到P 点之间距离，则带电体在P点处所产生的电势为：

对于规则均匀带电体，式(2)中的积分计算易于求解。 但对非均匀带电体则需要采用数值计算方法。

如图1 所示的均匀带电圆环，其半径为R，带电量为Q，圆环电荷线密度为λ。 现计算带电圆环在圆环中心O 点，以及圆环内任意一点p（x,y）处产生的电势。

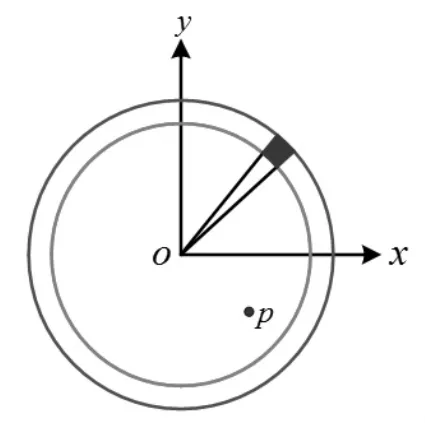
图1 均匀带电圆环示意图

对于圆环中心O 点的电势， 因圆环上所有点到达O 的点距离均为带电圆环的半径R，即式(2)中的r等于R，

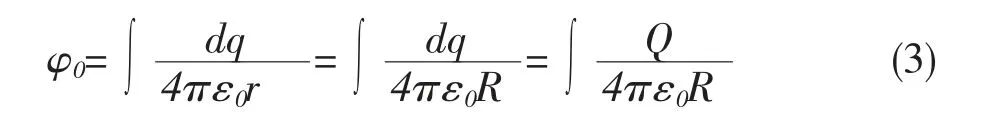
上述积分计算比较简便， 但对圆环内任意一点处产生的电势计算， 根据连续带电体在空间产生电势计算公式(2)，可得P（xp,yp）处的电势

若该带电圆环所带的电荷在圆环上并非均匀分布，则式(2)积分将变得更加复杂。 因此需要采用数值计算进行求解近似解。下文将对带电圆环在圆环内任意一点产生的电势为例，介绍数值求解过程，并将数值解与解析解比较分析。

二、均匀带电圆环电势解析解与数值解比较分析

（一）电势解析求解

P（xp，yp）点处的电势式(4)解析解求解如下，荷元在p 点处产生的电势之和。 基于此，首先将连续带电体作离散处理， 用离散分布的电荷替代连续带电体。将带电圆环分为N 等份，每个等份点上分布带电量为电荷， 则P 点电势为N 个带电量为的点电荷在p 点产生的电势叠加，即。当N 取值很大时， 该电势可近似代替均匀带电圆环在p 点产生的电势。

根据辅助角三角变换公式，以及二倍角公式，代入（5）得：

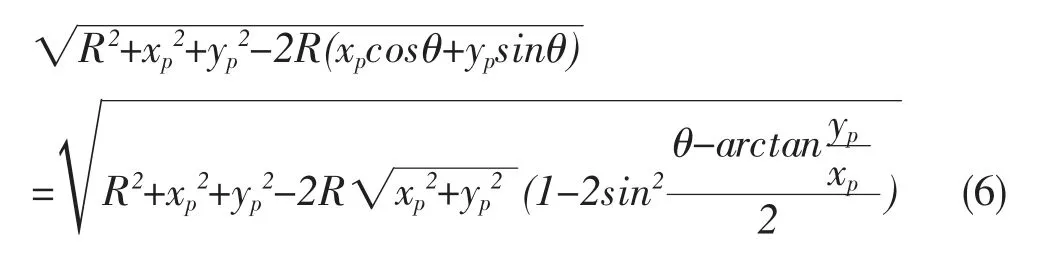
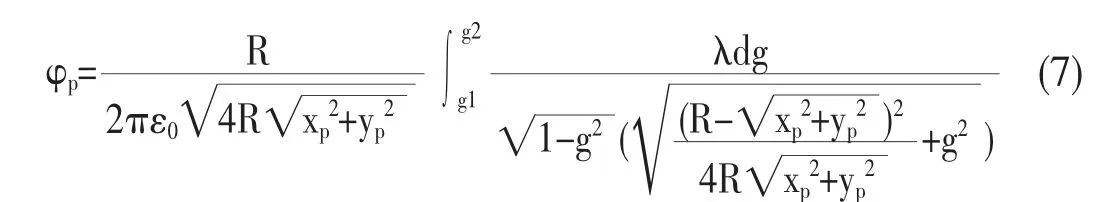
若带电圆环带电均匀，则式(7)可以进一步化简，由于带电圆环带电均匀即电荷分布具有对称性，为了计算方便，可以选取Op 为x 轴，则圆环内任意一点p(xp，0)所产生的电势，

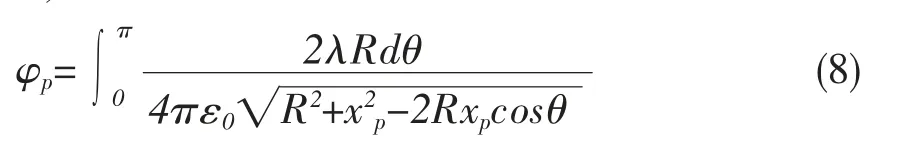
如图2 显示的是N=4 时， 整个圆环被4 等份，等分点分别为A1（xA1，yA1），A2（xA2，yA2），B1（xB1，yB1），B2（xB2，yB2），每个等分点上的电荷量为Q/4，每个等分点P 到达点的距离分别用rA1、rA2、rB1、rB2表示， 每个等分点上的电荷在p 点处产生的电势分别用φA1、φA2、φB1、φB2，则p 点的电势为各等分点在P 点产生的电势之和，可得点P 的电势为，通过上述的同样推导过程可得式(7)的等效式，

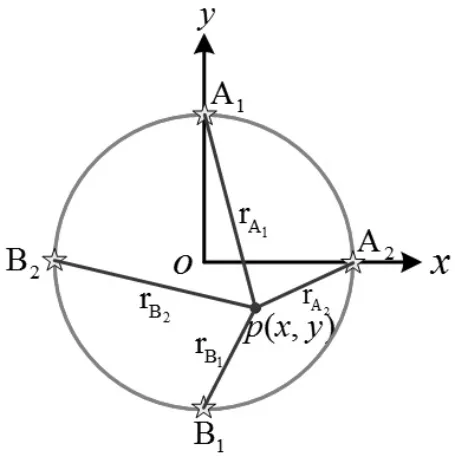
图2 带电圆环等效四等分点

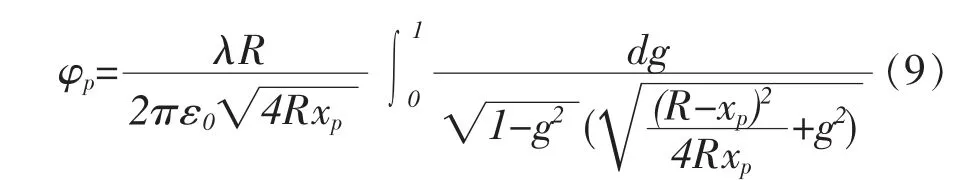
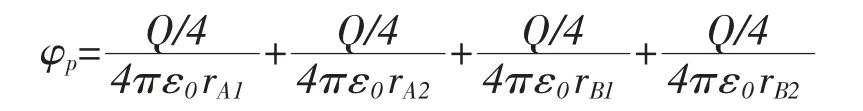
根据积分公式以及第一类非完全椭圆积分公式[4]

当N 取值很大时， 上述解可近似代替均匀带电圆环在P 点产生的电势。

如图3 所示的是带电量为Q， 半径为R=1 的均匀带电圆环在点p (0.2,0) 处产生的电势数值计算结果。 x 轴对应的是圆环的等分数，y 轴对应的是p 点的电势φp与Q/4πε0的比值。 解析解p 点的电势与Q/4πε0的比值为1.010，282，3。 通过图3 可以看出，随着圆环等分数N 的增加，p 点的电势与Q/4πε0的比值数值解逐渐收敛于1.010，3。

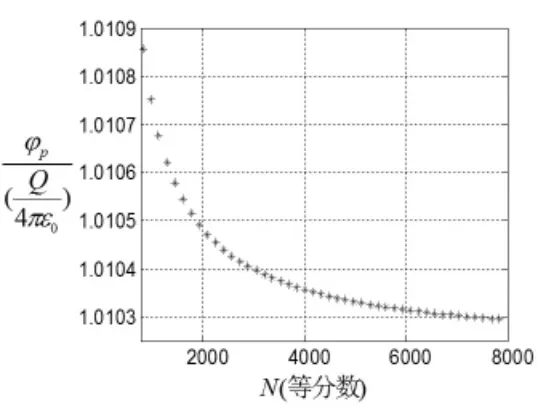
图3 不同N 值对应的点电势计算值

所有单位取国际标准单位制， 当xp=0.2m，yp=0m，R=1m 通过查表计算可得，

（二）电势数值求解

下面介绍均匀带电圆环所产生电势的数值解法。 根据电势叠加原理可知，p 点的电势等于所有电

三、复杂非规则带电面板电势数值计算

如图4 所示的平面带电体。 假设其电荷面密度为σ=1C/m2。求解空间点P(0.5,0.25,1)处产生的电势。基于上述数值计算思想， 需要将连续的面电荷离散到有限网格面上， 并将该网格面电荷集中在网格中心以点电荷代替该网格面电荷所产生的电势， 最后进行叠加计算得到数值解。 具体如下：

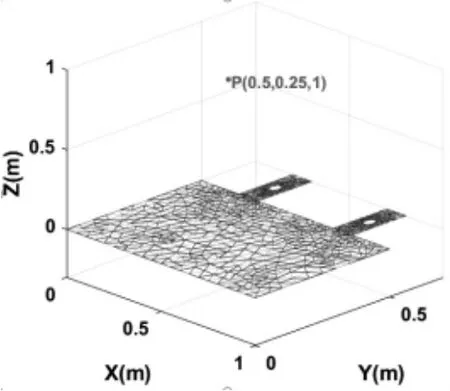
图4 非规则均匀带电体及网格划分

对带电体进行网格划分，结果如图4 所示，计算出每个三角形重心到P 点的距离， 根据点电荷在空间一点产生电势φp=q/4πε0r，累加计算可得P 点电势的数值解

四、开孔平行电极板间电势数值计算及分析

开孔电极板在静电除尘[5]中具有重要的应用且静电区内的电场直接影响静电除尘效率[6]，因此多孔电极板间的电场电势研究对多孔极板的设计具有指导意义。 下面利用上述介绍的数值计算方法研究不同结构的电极板间电势分布情况。

多孔极板几何结构如图5 所示， 九孔直径均为10mm，极板几何尺寸为100mm×100mm。 两极板之间的距离为10mm。 两极板均匀带电，电荷面密度分别为σ，-σ。

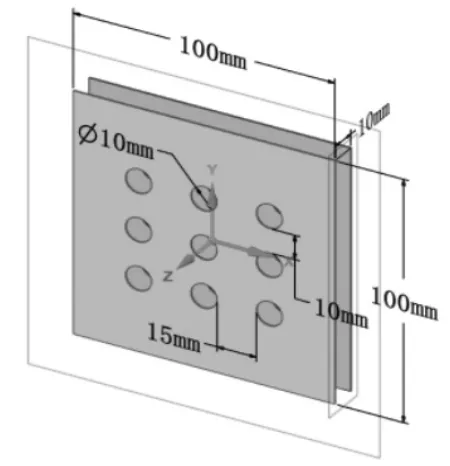
图5 多孔平行板电极结构

采用三角形网格对极板划分并采用电势叠加计算得YZ 面电势分布如图7 所示。

改变图6 极板的孔径大小,数值计算两极板间的等势线，其分布如图7 所示。

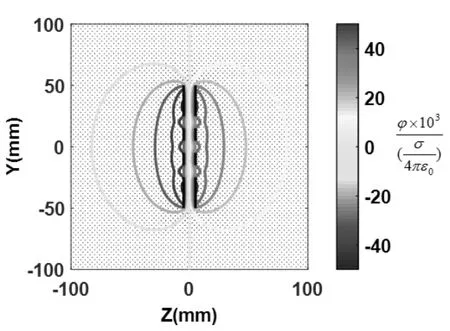
图6 多孔平行板电极YZ 面等势线分布图

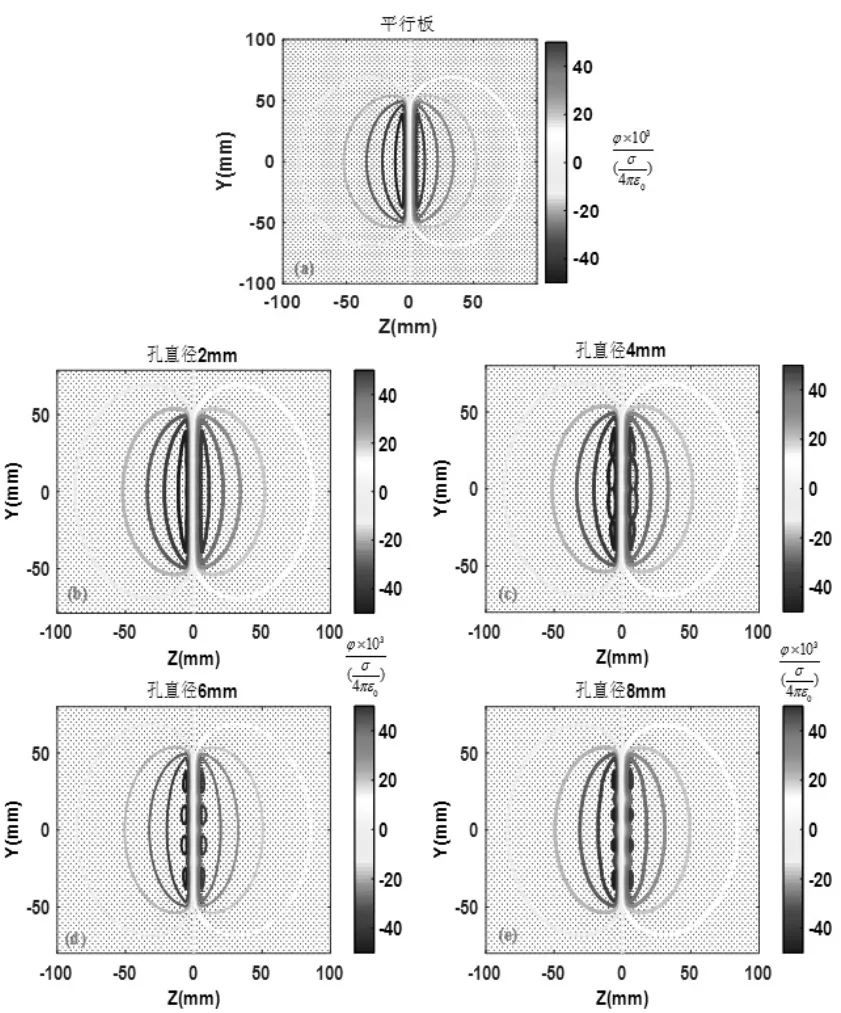
图7 平行板电极YZ 面等势线分布图

由图7 可知随着极板上孔径的减小， 两极板之间的等势线与无开孔平行板之间等势线差距逐渐减小。 取z 轴为2mm 处的电势值进行比较结果如图8所示。

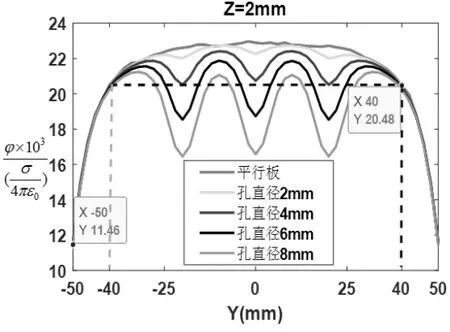
图8 平行板电极YZ 面在Z=2mm 处的电势

由图8 可知在Y=0mm 处，各电势相差较大。 无孔平行板在该处的， 其它孔径在该处的数值如表1 所示。

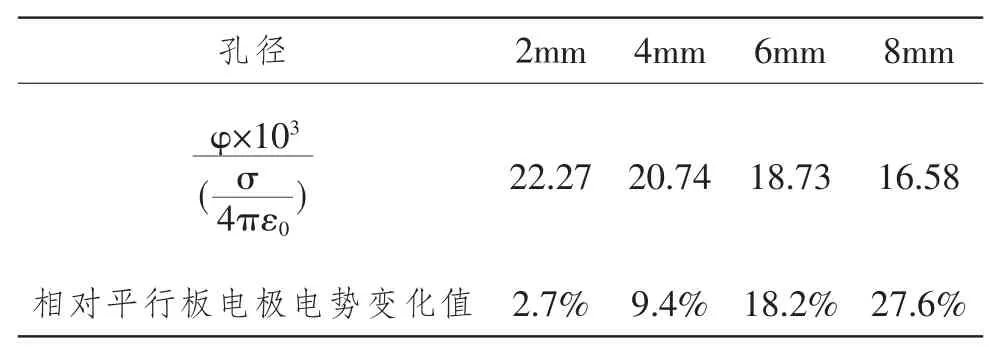
表1 不同孔径在Y=0mm,Z=2mm 处电势

由图8 可知， 有限大平行板间的电势呈现中间强两侧弱的分布。 取无孔平行板Y=0mm, Z=2mm 处电势的90%作为上限和下限值， 可以得到在离平板中心约80%的区间内具有较好的均匀性， 且在以平板为中心的60%区间内，电势仅有约4%的下降。 而在平板两端的边界区电势的下降可达中心电势的50%。 由此可知在有限大平行板的实际使用中，边界区电势均匀性较差， 应尽可能使用中心区域60%-80%面积。

对于极板开孔大小对电势分布的影响如表1 所示，随着电极板开孔直径的减小，两极板间的电势与无孔平行极板之间的电势变化减少， 在孔直径为8mm 时， 其产生的电势与无孔平行板电极产生的电势相差27.6%。在孔直径为2mm 时，其产生的电势与无孔平行板电极产生的电势仅相差2.7%。 由此看出平行板上的小孔径开孔对极板间电势分布影响较小。 上述结果也可以用在对电极板上开孔布置朗缪尔探针[7]测量两极板间的等离子体相关参数的结构设计中。 为开孔电极板间的电势分布计算提供数值解法。

五、结论

本文通过对均匀带电圆环内任意一点的电势计算为例，介绍其数值计算方法，并对其结果与解析解进行比较分析。 在此基础上介绍了数值方法计算复杂结构带电体在空间产生的电势，这为加深学生对数值计算意义的理解具有重要的意义。 其次文中采用数值方法研究了不同开孔数量和孔径大小对多孔平行板的电势分布影响，得到在多孔且小孔径的条件下只会有限的改变不开孔时平行板空间电势分布的结论。 这一结论也为采用朗缪尔探针测量极板间等离子体参数装置的结构设计提供一定的理论指导。