机匣螺栓连接虚拟薄层单元建模方法

陈云，臧朝平，杨志强

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

航空发动机中的许多连接结构对发动机的动力学特性有很大的影响，比如机匣螺栓连接、转子套齿连接等[1]。在对航空发动机整机动力学特性分析时，前人大都将连接作为刚性处理，这样会增加整机模型的总体刚度，不符合实际发动机结构特性，严重影响整机模型与实际结构动力学特性的吻合程度。在早期设计阶段，没有物理样机，无法准确建立连接模型，也就无法获取连接参数，故连接建模难度非常大。

针对螺栓连接结构，国内外学者进行了一系列探索研究，发现连接对结构的刚度和阻尼有很大的影响，尤其是金属结构，其产生的阻尼可以达到材料阻尼的10～100倍[2-3]。KIM J等[4]研究了基于弹簧阻尼法的螺栓接触分析法；SONG Y等[5]研究了采用梁单元模拟螺栓连接的方法；AHMADIAN H等[6]采用薄层单元法，将连接结构的接触法兰面等效为厚度很薄的实体单元，建立动力学建模，并利用优化算法对薄层材料参数进行了修正。马双超[7]在模拟螺栓连接时，采用了薄层单元建模的方法，通过调整薄层单元的材料参数来识别连接处的实际刚度。孙衍山等[8]研究了螺栓预紧力、螺栓分布和螺栓数量对机匣抗弯刚度和振动频率的影响。姚星宇等[9]提出了航空发动机复杂螺栓连接结构的连接刚度理论表达式,并进一步研究了航空发动机螺栓连接载荷、结构参数对连接刚度的影响规律。刘宗魁[10]运用分区薄层单元模拟航空发动机机匣螺栓连接结构。刘丁[11]通过建模仿真验证了薄层单元法在建模仿真中的可行性。目前，螺栓连接采用薄层单元建模的方式得到了一定的认可，但是AHMADIAN H、刘宗魁等人建立的均为实体薄层单元，机匣连接件建模采用实体薄层会导致机匣轴向位置发生微量偏移，连接机匣数量较多的情况下偏移量会不断累积，最终造成整机轴向位置定位出现较大误差。为避免这个误差的出现，本文研究了薄层单元建模原理，提出虚拟薄层单元法代替实体薄层单元法完成机匣连接建模，并用相关分析理论验证了虚拟薄层单元法的可靠性。

1 基本原理与方法简介

1.1 薄层单元建模原理

本文采用8节点六面体单元建立实体薄层，如图1(a)所示；4节点板壳单元建立虚拟薄层如图1(b)所示。为便于计算引入局部坐标系(ξ，η，ζ)。薄层单元内任意节点坐标为(Xi，Yi，Zi)，节点位移为(Ui，Vi，Wi)。

图1 薄层单元

薄层单元的形函数为

(1)

薄层单元中任一点的位移可表示为

(2)

薄层单元内任一点的坐标可表示为

(3)

形函数是在局部坐标中建立的，在由单元节点位移求单元应变时，需要求解形函数在总体坐标中的导数，因而需要将局部坐标中的形函数表达式转换到整体坐标中，由偏微分法则得

(4)

(5)

对于尺寸为l1×l2×d的薄层单元，根据虚位移原理得到其虚功方程

(6)

式中：l1、l2分别是薄层单元x和y方向的长度；d是薄层单元在局部坐标系z方向的厚度；K是通过等参变换得到的在自然坐标系ξ、η、ζ下的单元刚度矩阵。需要对积分的单元体积进行变换，根据微分知识可得

(7)

式中i、j、k分别是沿x、y、z方向的单位矢量。微元体的体积可由dξ，dη，dζ的矢量混合积求得：

dV=dξ(dη×dζ)=|J|dξdηdζ

(8)

进而可得单元刚度矩阵的表达式为

(9)

式中K是雅克比矩阵。由局部坐标转换到自然坐标的等参变换得到，二者方向一致时J的表达式为

(10)

根据高斯积分，刚度矩阵K的表达式为

det([J(ξi，ηj，ζk)])wξ，iwη，jwζ，k

(11)

式中wξ,i、wη,j、wζ,k是高斯积分权函数。

假设薄层单元厚度d远远小于长度l1和宽度l2，相关研究表明当厚度d趋近于0时单元应变(εx,εy,εxy)和单元应力(δx,δy,δxy)可以忽略。此时可以把接触面法向{e}n和接触面切向{e}Tx，{e}Ty分别定义为局部坐标，x、y和z的方向。同理，应力δz、δxz和δyz分别对应tn、tTx和tTy；应变εz、2εxz和2εyz分别对应εn、γTx和γTy，则本构方程可以转化为

(12)

式中En和GT分别是弹性模量和切变模量。对于各向同性材料，En和GT之间的关系式为

(13)

1.2 相关分析理论

相关分析是用于评价有限元模型预测的结果与参考数据的接近程度，从而确定有限元结果和参考数据对应的模态对，可用以验证有限元模型的可靠性。模态置信准则(modal assurance criterion，MAC)，是工程上应用最为广泛的模态相关性分析方法。MAC基于模态向量之间的加权正交性，通过计算两个模态向量之间夹角余弦值的平方来判断模态对，其定义如下：

(14)

式中：φr和φq分别代表第r阶和第q阶模态向量；*代表共轭转置。MAC值介于0～1之间，其>0.9说明两个模态向量有很好的一致性，两阶对应的模态为相关的模态对；若接近0则说明两阶模态向量有较大的差异，不是对应模态。在工程中，若两阶模态的MAC值>0.6，就可认为二者是相关模态对。

2 机匣薄层单元连接建模

2.1 机匣连接简化模型

机匣螺栓连接简化模型如图 2所示，上安装法兰1与下安装法兰3通过螺栓2a连接。实体薄层单元的简化模型如图 3(a)所示，上安装法兰1与下安装法兰3通过实体薄层2b连接。虚拟薄层单元的简化模型如图 3(b)所示，上安装法兰1与下安装法兰3通过虚拟薄层2c连接。薄层单元连接结构的各部分的轴向刚度表达式为

图2 螺栓连接简化模型

图3 薄层连接简化模型

(15)

式中：Ei为被连接件的弹性模量；Ai为有效横截面积；Li为结构的轴向长度。

把上安装法兰1、薄层单元2b(2c)和下安装法兰3视为串联的弹簧结构，可得薄层单元连接结构的轴向刚度表达式为

(16)

由式(15)和式(16)可得薄层等效弹性模量

(17)

式中：k为螺栓连接刚度，具体的计算方法可参照文献[9]；k1、k3为安装法兰的轴向刚度；A2是薄层与法兰的接触面积；L2是薄层的厚度。

2.2 机匣连接有限元模型

航空发动机机匣大多是带有凸台、凹槽或者肋板等细节特征的薄壁圆筒结构。建立机匣连接结构有限元模型时，忽略这些细节特征可以有效提高计算效率。本文建立的机匣虚拟薄层连接有限元模型如图 4所示。机匣与薄层均为各向同性材料，弹性模量为210GPa，密度为7 800kg/m3，泊松比为0.3。根据参考文献[9]，薄层单元厚度均设置为1mm。实体薄层连接的机匣将产生1mm的轴向位置偏移，虚拟薄层连接的机匣可以有效地避免这个误差，而且虚拟薄层的厚度可以设置为实常数，修改实常数值能够方便快捷地研究薄层厚度的改变对连接刚度的影响。

图4 机匣虚拟薄层连接有限元模型

3 相关分析

对两种薄层连接模型分别计算自由状态下前5阶模态，忽略重模态，得到的各阶模态频率如表 1所示。可见与实体薄层连接模型比较，虚拟薄层连接模型各阶频率有所降低，最大误差为-4.5%，最小误差为-0.1%。如图 5所示，两种模型各阶匹配模态振型基本一致，振型相关性较好。前5阶主要是后面机匣的节径振动，随着频率的增大，节径数逐渐增多。连接处未出现局部振动模态，说明薄层连接刚性足够，与实际螺栓连接情况相符。如图 6所示，各阶MAC值均>0.8，说明两种连接模型接近程度非常高。

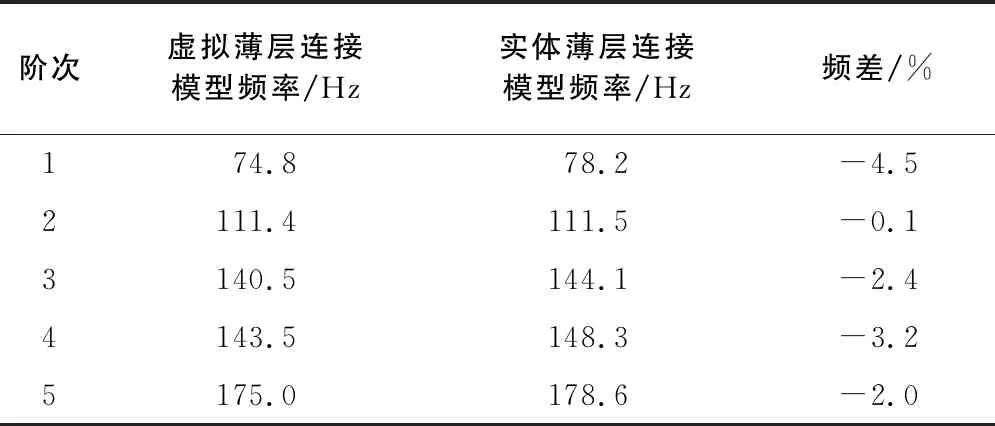
表1 机匣实体/虚拟薄层连接模型前5阶频率

图5 机匣实体/虚拟薄层连接模型前5阶振型

图6 薄层连接模型相关分析MAC值

4 结语

本文针对航空发动机机匣螺栓连接结构建模方法展开研究。在实体薄层基础上，提出虚拟薄层代替螺栓连接的建模方法，并用相关分析理论验证虚拟薄层连接模型的可靠性。研究结果表明：虚拟薄层单元法建立的连接模型比实体薄层单元法建立的连接模型各阶频率略有降低，最大误差为-4.5%，各阶模态MAC值均>0.8。该建模方法能较好地模拟机匣螺栓连接，并能有效避免实体薄层单元法所产生的机匣轴向位置偏移。虚拟薄层连接模型各阶频率偏低可能是虚拟薄层自身刚度偏低所致，后续可以对虚拟薄层的弹性模量进行调整，减小频率误差，提高连接模型的可靠度。