具Holling-IV型发生率的时滞SEIR模型稳定性与Hopf分支分析

郭 宇,朱惠延，贺芳芳

(南华大学数理学院，中国 衡阳 421001)

众所周知，数学建模在传染病的研究中具有重要意义，它可为了解疾病的传播机理及预测疾病未来的发展趋势提供理论参考，从而有助于对疾病进行有效的控制[1-3]。

受以上文献的启发，本文将考虑一类具有Holling-IV型发生率且带有潜伏期时滞τ的SEIR传染病模型，构建模型如下：

(1)

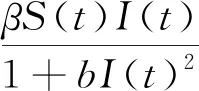
由于模型(1)前3个方程不含R变量，因此只需考虑模型(1)的前3个方程：

(2)

设模型(2)初始条件Φ=(Φ1,Φ2,Φ3)定义在Banach空间C上，

其中Φi(θ)≥0,θ∈[-τ,0]，这里假设Φi(0)>0(i=1,2,3)。

将模型(2)中三个方程相加得到：

1 平衡点存在性

接下来考虑模型(2)地方病平衡点出现情况。令模型(2)方程右端等于0，得到

通过以上方程可以求得地方病平衡点P1(S*,E*,I*)，

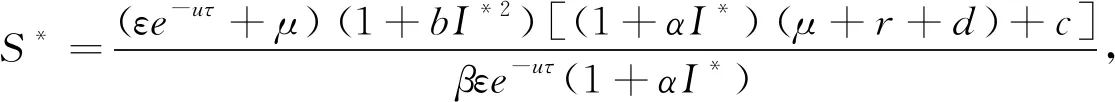
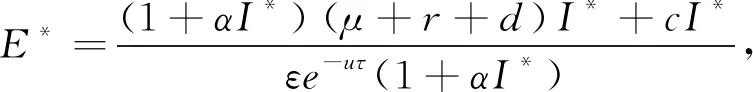
I*为三次方程f(I)=a1I3+a2I2+a3I+a4=0的正根，其中

a1=μαb(ε+μeuτ)(μ+r+d),

a2=(ε+μeuτ)(μ+r+d)(αβ+μb)+μcb(ε+μeuτ),

a3=cβ(ε+μeuτ)+(ε+μeuτ)(μ+r+d)(β+μα)-Aβεα,

a4=μ(ε+μeuτ)(d+μ+r+c)(1-R0)。

作如下变换：

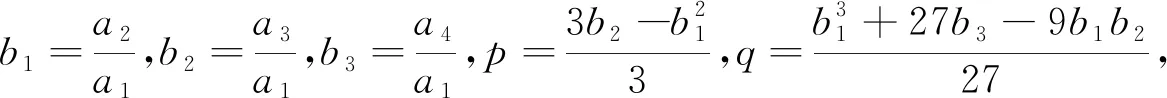
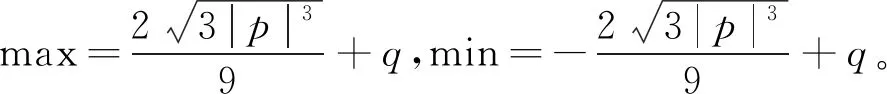
通过以上变换，f(I)转化为

f(I)=I3+pI+q。

(3)

现考虑式(3)的系数与正根的关系：

1)当p>0时，显然f′(I)>0，f(I)为增函数，当且仅当q<0时，方程(3)存在唯一正根；

2)当p=0时，当且仅当q>0时，方程(3)存在唯一正根；

3)当p<0时，根据三次函数特性知f(I)先增再减再增，考虑以下情况：

i)q>0时，

a.若min=0，方程(3)存在两个相同的正实根；

b.若min<0，方程(3)存在两个不同的正实根；

c.若min>0，方程(3)不存在正根；

ii)q=0时，方程(3)存在唯一正根；

iii)q<0时，方程(3)存在唯一正根。

定理11)当p<0，q>0，min<0时，模型(2)存在两个地方病平衡点；

2)当p>0，q<0或p=0，q>0或p<0，q>0，min=0或p<0，q=0或p<0，q<0时，模型(2)存在唯一地方病平衡点。

2 无病平衡点稳定性与Hopf分支分析

因此可以得到特征方程为：

(4)

显然，λ=-μ是特征方程(4)的一个负实根，令：

(5)

g(λ)可以化为下式：

λ2+c1λ+c2+(c3λ+c4)e-λτ=0。

(6)

其中

c1=(2μ+r+d+c)，c2=μ(μ+r+d+c),

c3=εe-μτ，c4=e-μτ[ε-R0(ε+μeuτ)](μ+r+d+c)。

当τ=0时，(6)式变为：

λ2+(c1+c3)λ+(c2+c4)=0。

(7)

由(7)可知，c1+c3=2μ+r+d+c+ε>0，c2+c4=(μ+ε)(μ+r+d+c)(1-R0)，所以当R0<1时，c2+c4>0，根据Routh-Hurwitz判据知方程(7)的根均具有负实部，因此在τ=0处无病平衡点P0是局部渐近稳定的。

当τ≠0时，由文献[16]中的结论，方程(6)有正实部的根当且仅当该方程存在纯虚根。假设λ=iω(ω>0)为方程(6)的一个纯虚根，代入方程(6)中分离实部与虚部得：

(8)

将方程(8)中两个式子分别平方相加得：

(9)

令ω2=y，则F(y)=y2+d1y+d2，其中

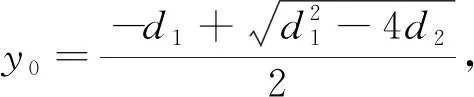
(10)

特征方程(6)对τ求导可得：

(11)

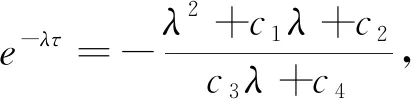
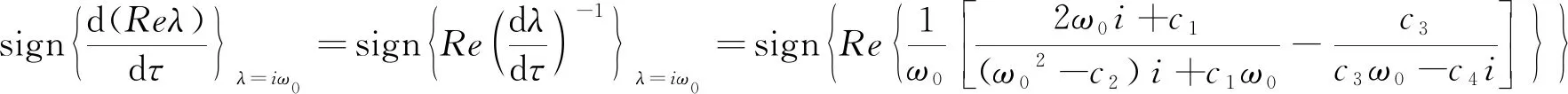
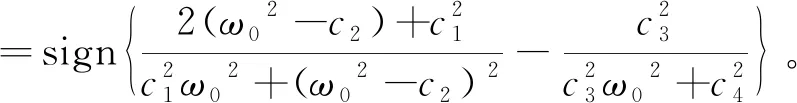
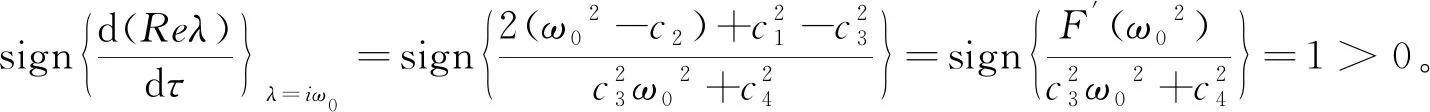
根据以上情况的讨论可以得到如下定理：

定理21)当R0<1，d1>0时，对于任意的τ∈[0,+∞)，模型(2)中无病平衡点P0存在且是局部渐近稳定的；

2)当R0<1，d2<0时，模型(2)中无病平衡点P0在τ∈[0,τ0)时是局部渐近稳定的，在τ∈(τ0,+∞)时是不稳定的；当τ=τ0时，模型(2)在平衡点P0处会出现Hopf分支。

3 无病平衡点全局稳定性分析

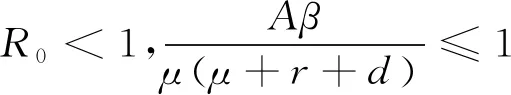
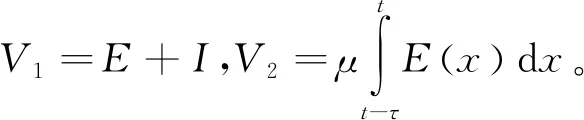
则V1沿模型(2)的导数：

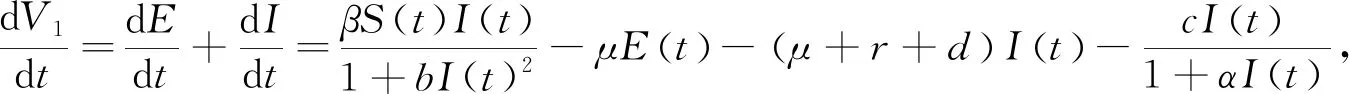
定义Lyapunov函数为V=V1+V2，因此可得：

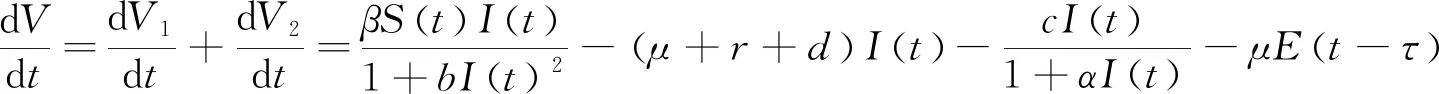
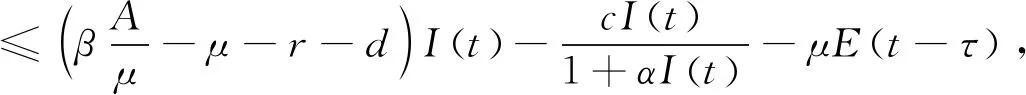
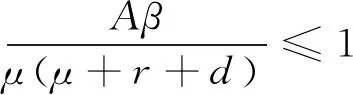
4 地方病平衡点局部稳定性与Hopf分支分析

根据文献[17]，可知f(I)=a1I3+a2I2+a3I+a4=0的函数系数与正根个数关系，即当R0>1时，模型(2)会存在唯一的地方病平衡点P1(S*,E*,I*)，将模型(2)在P1处线性化得到地方病平衡点的雅克比矩阵为：

因此对应的特征方程为：

|λI-J(P1)|=λ3+p1λ2+p2λ+p3+(q1λ2+q2λ+q3)e-λτ=0。

(12)

其中

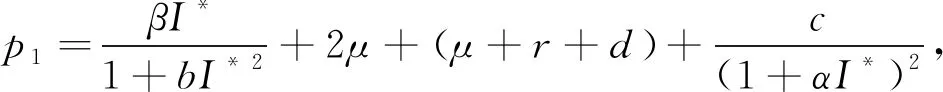
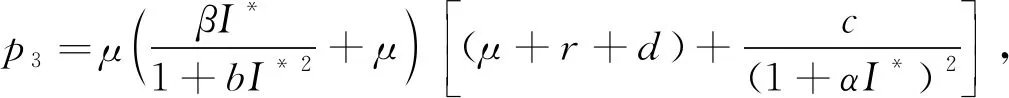
q1=εe-μτ,

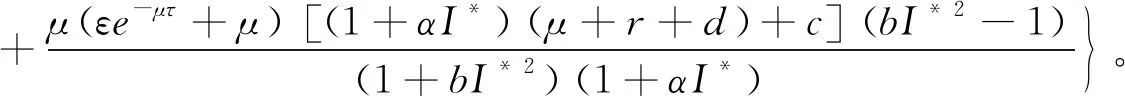
当τ=0时，方程(12)变为：

λ3+(p1+q1)λ2+(p2+q2)λ+(p3+q3)=0。

(13)

显然p1+q1>0，结合Routh-Hurwitz判据，若方程(13)还满足条件：

H1：p2+q2>0,p3+q3>0,(p1+q1)(p2+q2)-(p3+q3)>0，

则方程(13)的所有特征根实部均为负值，地方病平衡点P1(S*,E*,I*)是局部渐近稳定的。

接下来考虑当τ≠0时的情况，假设λ=iω(ω>0)为方程(12)的一个纯虚根，代入方程(12)中分离实部与虚部得

(14)

将方程(14)中两个式子分别平方相加得：

(15)

令ω2=z，则L(z)=z3+l1z2+l2z+l3，其中

根据方程L(z)，若简单条件

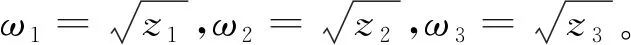
其中1≤k≤3,j=0,1,2，…。

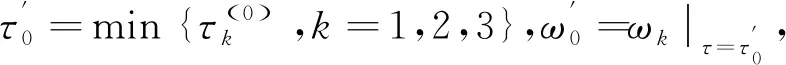
将λ=iω0代入并结合方程(12)得到

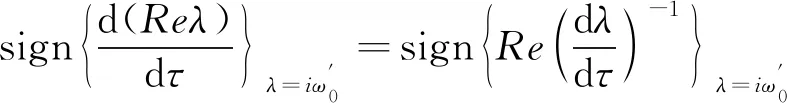
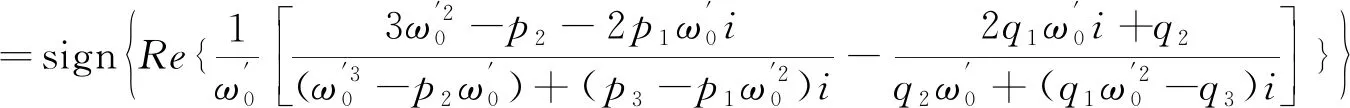
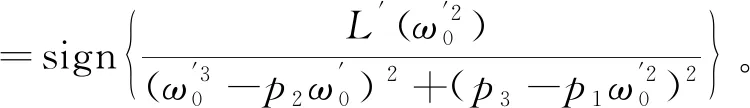
因此，只要满足条件：

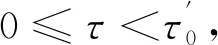
5 数值模拟

为了验证所得结论，对模型(2)选取不同参数值进行数值模拟。

(i)选取参数值A=0.8，β=0.2，ε=0.6，μ=0.2，b=1，c=0.2，α=1，r=0.08，d=0.2，可知模型(2)存在唯一无病平衡点P0=(4,0,0)，此时R0=0.882 4<1，d1=0.142 4>0，分别选取不同时滞τ=0与τ=10.5进行数值模拟，如图1和图2所示，可以看出随着时间变化曲线最终达到稳定，疾病将会被消灭，P0是局部渐近稳定的，定理2得到验证。

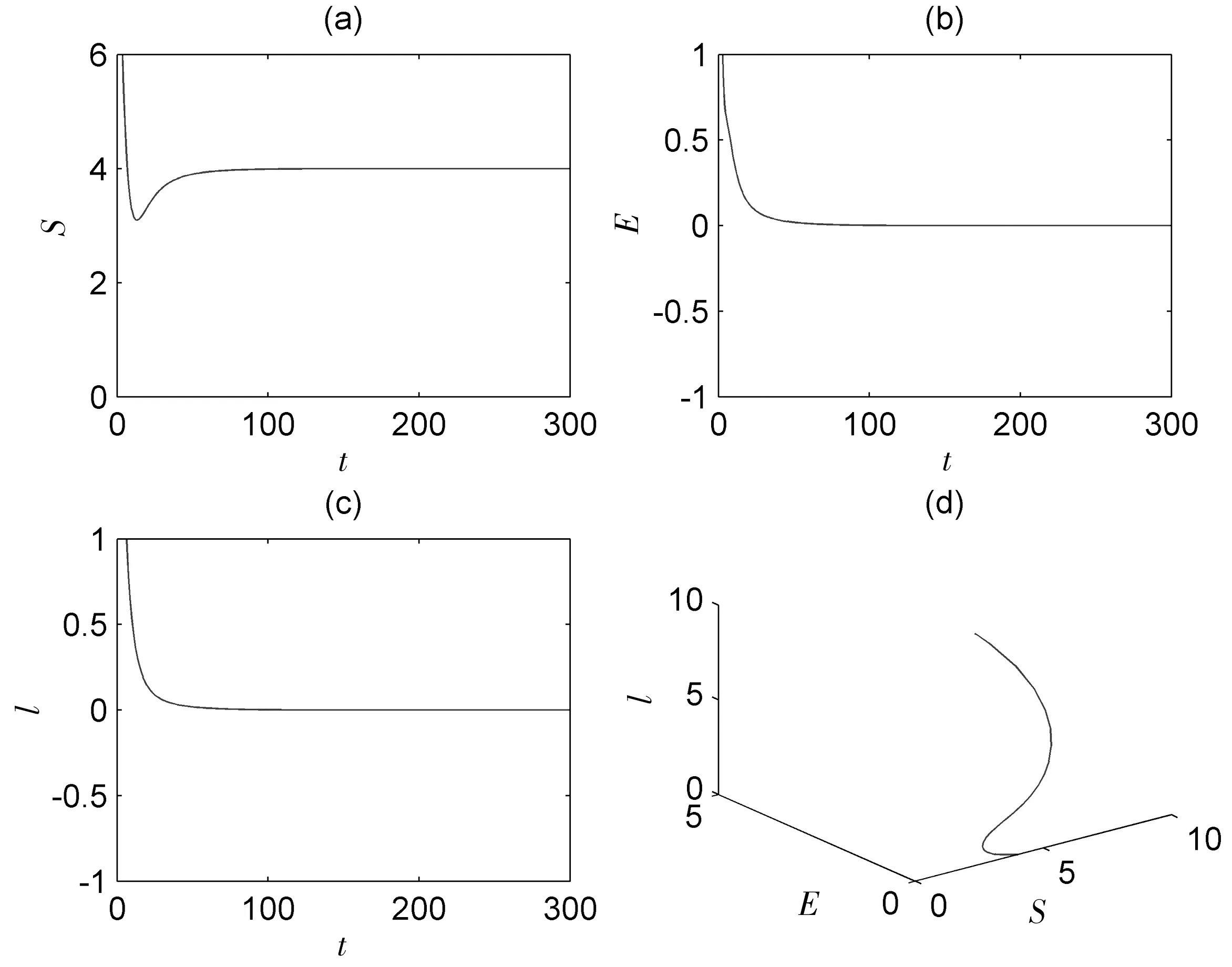
图1 当τ=0,R0<1时模型(2)的时序图与相图

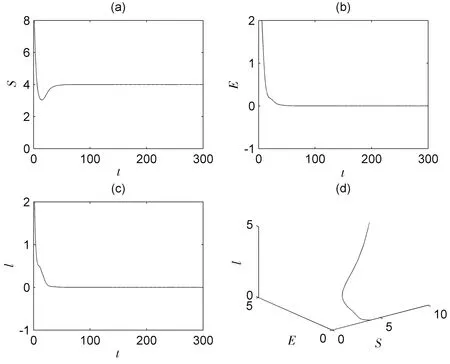
图2 当τ=10.5,R0<1时模型(2)的时序图与相图

(ii)选取参数值A=1.5，β=0.25，ε=0.8，μ=0.15，b=1，c=0.1，α=1，r=0.15，d=0.05，此时R0=4.678 4>1，模型(2)还存在唯一地方病平衡点P1，当τ=0时，易得P1=(5.603 1,0.694 2,1.419 3)，由图3验证可知P1为局部渐近稳定的。

图3 当R0>1,τ=0时模型(2)的时序图与相图

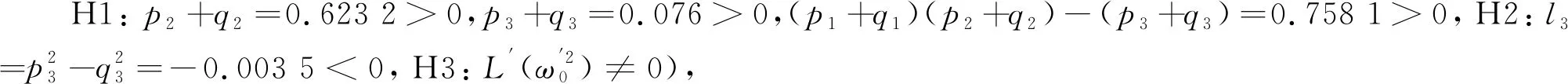
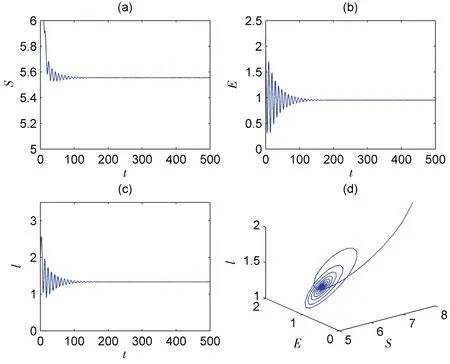
图4 当时模型(2)的时序图与相图

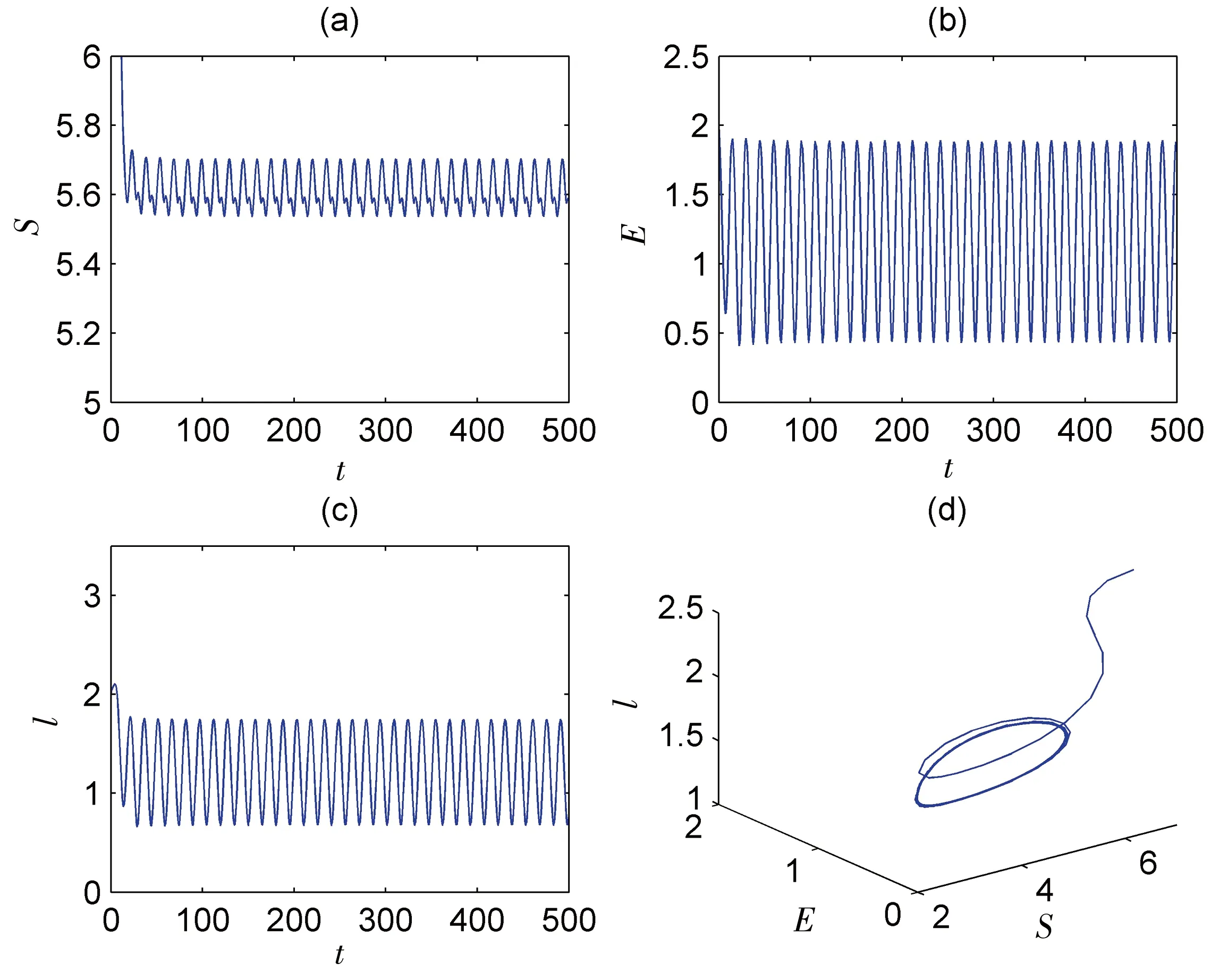
图5 当时模型(2)的时序图与相图

6 结论