改进蝠鲼觅食优化算法的配电网故障定位

张荣升，刘丽桑，徐辉，柯程扬

(1.福建工程学院电子电气与物理学院，福建 福州 350118；2.工业自动化福建省高校工程研究中心，福建 福州 350118)

当前，清洁能源与新能源快速发展，集低能耗、清洁环保、灵活供电等优点于一体的分布式电源(distributed generation，DG )被大力推广。当大量清洁能源被接入配电网后，电力系统的容量和规模被扩大，配电网的内部构造以及系统工作方式发生改变，电网结构愈加复杂，电流的传输方向不再单一。在含DG的配电网中，DG的运行与退出以及过流信息发生改变或信息不完整等问题，都使得故障定位更加复杂。

理论上，智能优化算法容错性较好，具有全局寻优收敛性，适用于配电网故障区段定位[1]。但在实际应用中，因算法计算过程的随机性不能完全避免，以致智能优化算法在收敛过程陷入部分最佳状态。文献[2]联合量子计算与免疫算法，缩小了种群规模，在系统多区段同时故障以及节点信息不完整的情况下，提高了故障定位的准确率。文献[3][4]分别将鲸鱼算法与蝠鲼觅食算法应用到配电网故障定位中，搜索机制独特，定位效果均优于传统的粒子群算法、遗传算法，但在节点信息发生遗失或改变时，容错能力会降低，导致定位结果出错。文献[5]将优化改良后的蚁群算法应用到故障区段检测中，改正了蚁群算法计算慢、求解能力不足的缺点，但算法鲁棒性差，寻优结果不稳定。文献[6]利用多种算法混合计算的策略对粒子群算法进行优化，故障区段的定位速度显著提高，但算法在求解过程中更新局部极值能力的不足、故障定位的准确率不稳定。

基于上述研究成果，本研究提出了改进基于阈值反馈蝠鲼觅食优化(threshold feedback MRFO,TFMRFO)的多电源配电网系统检测故障的方法减少算法寻优过程中学习入局部最优的迭代次数，以提高配电网故障定立的准确率与速率。

1 多电源配电网故障定位模型

在基于智能算法的配电网故障定位中，馈线终端单元(feeder terminal unit，FTU)是将线路电流信息输送到系统终端的载体，可以随时掌控配电网线路的运行状态。系统以节点开关上每个FTU上报的故障信息组合而成的向量为依据，联合多电源配电网的拓扑结构建成适应度函数，利用各种寻优算法求解适应度函数的最佳结果，顺利检测出配电网故障位置[7]。为了对含多电源的配电网进行仿真实验，在传统的配电网模型中加入了分布式电源。以图1多电源配电网简易模型为例，建立了改进的故障信息编码方法、开关函数以及适应度函数。

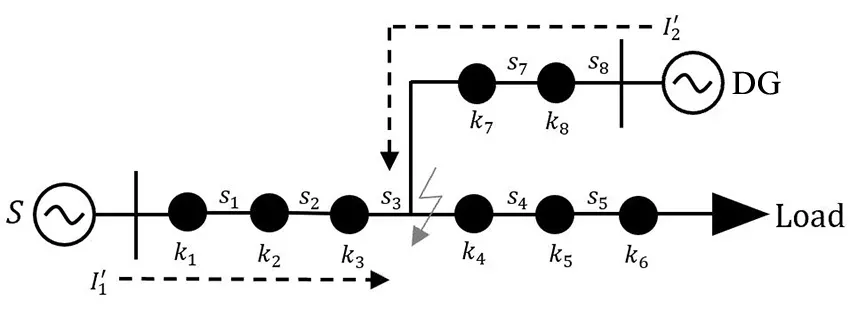
图1 多源配电网简易模型Fig.1 Simple multi-power distribution network model

1.1 故障信息编码

将配电网模型中装有FTU设备的开关节点定义为分段开关，在构造的配电网模型中分别用k1～k8表示。这些开关节点将整个配电网划分为若干个区段s1～s8，将开关节点与线路区段联系起来[8]。线路区段发生故障时，故障电流只源于靠近电源的上游节点，I′1、I′2为故障电流方向，由于在多源配电网中，潮流方向不在唯一，0-1编码不再适用于目前的电网结构，故将系统电源流向故障点的方向定义为参考方向。

开关节点i的实际线路测量值用Ii表示，新的编码方式为：Ii=1表示FTU监测到电流方向与该节点编码的参考方向一致；反之，Ii=-1；线路中没有检测到流过信息时，Ii=0；对于有故障的区段，令si=1; 对无故障的区段，令si=0。

1.2 开关函数构造与验证

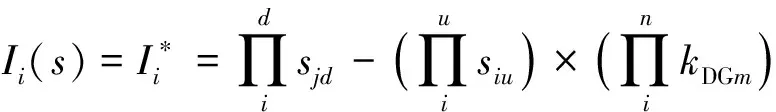
(1)

式中，Π表示逻辑“或”的叠加运算；开关节点i的上、下游线路的运行状态用siu、sid表示，线路发生故障时，siu或sid的值为“1”，无故障时值为“0”；n为系统中含有分布式电源个数；节点i上、下游全部区段的个数分别用u、d表示；分布式电源m运行状况用kDGm表示，电源投入配电网运行时，kDGm=1，切除时，kDGm=0。分布式电源数学模型的构造决定了新的开关函数在含有DG的配电网络中能否对线路运行状态进行准确表达。

1.3 适应度函数构造与验证

适应度函数的求解精度是配电网故障区段完成精准定位的保障，表示配电网发生故障时，FTU上传至系统终端的实际测量值与通过构造的开关函数计算出来的期望值之间的差异[9]。基于智能算法的配电网故障定位过程即为适应度函数求解全局最小值的过程。为了避免函数求解出现多解，根据“最小集”原理[10]，在原始的适应度函数中加入系统中发生故障区段数量模块，使求得的解最小，保证了解的唯一性，减少定位结果发生误判。本研究所采用的适应度函数如式(2)所示。

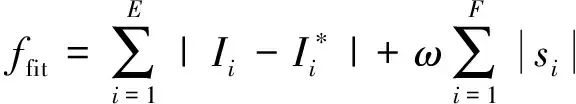
(2)

2 TFMRFO算法原理

蝠鲼觅食优化(manta ray foraging optimization, MRFO)算法是由ZHAO Weiguo等[11]在2020年提出的智能优化算法，具有优化速度快、局部搜索能力强、参数少等优点但也存在定位速度慢、对故障区段定位能力不足等问题。本研究基于MRFO算法提出了基于阈值反馈蝠鲼觅食优化算法TFMRFO，引用Limit阈值控制算法迭代次数，降低算法在定位过程中因陷入局部最优而导致故障区段发生误判的可能性，融合信息反馈机制，在蝠鲼个体位置更新后期，通过种群中最差点向最优点的移动，加快种群最差位置向最优位置靠拢，从而改善算法全局寻优性能，加快了故障定位速率；后期利用Sigmoid函数将连续求解问题转化为0-1非线性整数优化问题，输出33个只包含{0,1}元素的结果向量，找出系统中发生故障的位置。

2.1 MRFO算法原理

MRFO算法由蝠鲼链式捕食、旋风式捕食、筋斗式捕食3种捕食策略引申而来。在链式觅食阶段，蝠鲼群体紧密排成一队，呈一条首尾相连的长链。领头个体在队伍最前方觅食，其他个体跟随其后，觅食前面个体遗漏的食物。除此之外，群体会朝着食物最多的地方游行，所有个体都会被当前最优位置和其前边位置取代，该种位置更新方式数学模型如式(3)(4)所示。

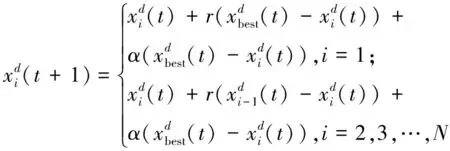
(3)

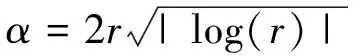
(4)

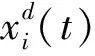
当蝠鲼群发现食物时，它们会将队伍形成一条漩涡状的捕食链游向食物，将食物牢牢围住。此时算法进入旋风式觅食阶段。当t/T>rand，所有个体将以食物作为参考点，进行下一步的搜寻，其更新模式如式(5)(6)所示。

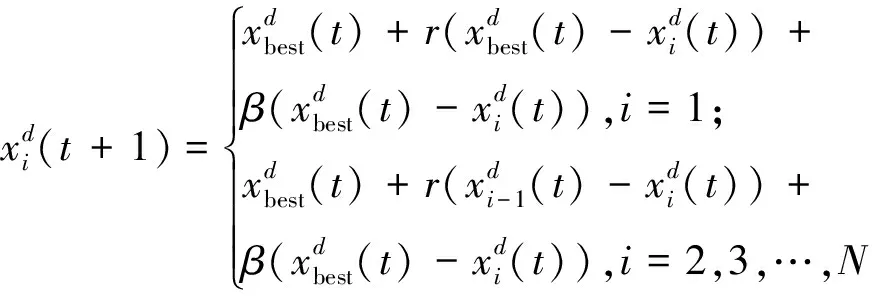
(5)

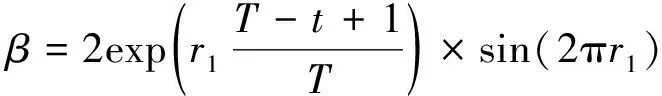
(6)

式中，β为权重因子；T为总迭代次数；r1为(0,1)随机数。当t/T≤rand，优化参考点发生改变，为了进一步加强全局计算，在整个寻优空间随机位置作为参考点，此时每个个体的寻优能力为整个优化过程的主要阶段，使MRFO能够在整个搜索空间内进行全方位地搜寻，描述这一过程的数学方程如式(7)(8)所示。

(7)

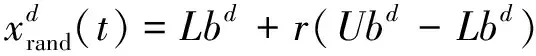
(8)

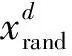
蝠鲼在捕食过程中，个体在筋斗范围内可以移动到任何一个新位置。一般群体会选择当前最优位置作为参考点，将其当前位置另一侧作为目标点成镜像关系进行捕食。这一阶段也是MRFO算法的关键阶段，因为在捕食过程中群体总是围绕着最优点来进行位置更新。其数学模型表达如式(9)所示。

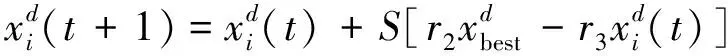
(9)

式中，i=1,2,…,N；决定翻滚范围的筋斗因子用S表示，取S=2；r2、r3为(0,1)随机数。

2.2 TFMRFO算法改进原理

2.2.1 Limit阈值原理

Limit阈值机制是通过观察可行解的停滞次数是否达到预先设定的极限值来进行循环迭代，若在Limit迭代中某个个体的位置没有发生改变，则抛弃当前解，继续下一代的进化重新生成新解[12]。在算法寻优过程中，蝠鲼个体将慢慢向猎物位置靠近，种群多样性降低，算法进入局部循环迭代状态的可能性增大，若不能及时迭代更新将直接导致求解出错。因此，引入Limit阈值的方法有效地控制MRFO算法陷入局部极值时的迭代次数，使得算法尽快更新局部所得解，MRFO算法在整个求解空间内的寻优能力得到加强。算法改进后的优化能力取决于阈值Limit的取值，一般将局部迭代累加次数控制在总迭代次数的5%，若取值过大则算法改进效果不明显；过小则算法局域内迭代频繁，导致局域范围内的搜索性能变差，全局收敛速度下降。

2.2.2 信息反馈原理

在MRFO算法中，蝠鲼的运动轨迹因猎物的位置变化而改变，运动方式单一。但在实际的觅食过程中，蝠鲼种群之间会进行位置信息交流，通过信息反馈，距离猎物较远的蝠鲼个体能快速跟随距离猎物近的个体游动，算法的计算速度得到进一步改善，因此融合交流反馈策略来提高算法的寻优速度与精度[13]。信息反馈阶段的数学表达式如式(10)所示。

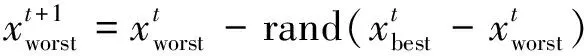
(10)

2.2.3 Sigmoid函数离散化变换

MRFO算法主要用于函数在连续空间内的求解问题，若要解决工程中配电网故障定位问题需要对原始算法进行离散化处理[14]。由第1.1线路状态的编码方式可知，用{1,0}表示线路中有无故障。故需要将MRFO算法离散为二进制空间的优化算法，结合概率映射的方法优化蝠鲼个体的位置更新算式，下一代蝠鲼个体的位置变化由Sigmoid 函数将个体位置转化到{1,0}集合的概率决定。其更新公式如式(11)(12)所示。

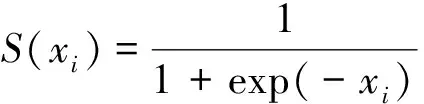
(11)

(12)

式中，xi表示第i个蝠鲼个体的位置；rand为[0,1]的随机数；yi表示二进制转换后的向量元素。

3 基于TFMRFO算法的故障定位

3.1 TFMRFO算法改进流程

阈值反馈蝠鲼觅食算法的具体改进步骤如下：

(1)种群规模设为N，全局最大迭代次数设为T，当前的迭代次数设为t，求解维度设为d，局部停滞次数设为tr，迭代阈值设为Limit；

(2)随机产生个体位置，并计算当前适应度值，得到当前最优位置xbest及求得当前最优适应度值为fbest，完成种群初始化；

(3)根据式(3)-(9)进入算法主循环；

(4)判断当前个体是否为当前最优，满足则进行Step6，否则记录当前解的局部停滞次数;

(5)根据式(9)更新个体位置；

(6)选择最差个体位置xworst，根据式(10)更新当前个体位置；

(7)计算每个个体的适应度值，根据新的适应度得到个体最优解x′best及全局最优解f′best；

(8)判断是否达到Limit阈值，满足则执行(2)，否则执行第(9)步；

(9)判断是否满足t≥T，是则执行步骤(10)，否则执行步骤(2)；

(10)使用Sigmoid函数对实数向量进行离散化处理。将x=[x1,x2,…,xn]转化为二进制向量y=[y1,y2,…,yn]。

3.2 故障定位流程

首先，根据上述故障定位数学模型建立仿真新系统，并对不同故障类型做出故障假设；然后，针对原始MRFO算法的缺陷，通过多策略融合的方式进行改进，并利用Sigmoid函数将其输出结果进行二进制转换；与此同时，利用FTU将节点故障信息转化为向量参数，将每个节点状态输入到TFMRFO算法中进行故障区段搜索。最终，输出定位结果向量，定位出具体的故障区段。基于TFMRFO算法的配电网故障区段检测方法的详细运行流程如图2所示。

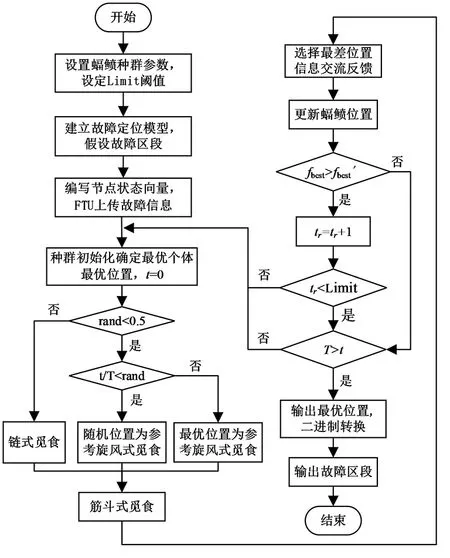
图2 TFMRFO算法故障定位流程Fig.2 Fault location flow of TFMRFO algorithm

4 算例分析

实验在Matlab R2020b上搭建仿真平台，构建配电网故障定位模型，并对基于TFMRFO算法的求解方法进行建模仿真。种群规模N=50，解空间内最大迭代次数T=60，阈值Limit=3。为了验证TFMRFO算法能否在配电网故障区段检测中合理运用，本研究选取经典矩阵算法、遗传算法(genetic algorithm，GA )、MRFO算法、混沌反馈鲸鱼算法(CFAWOA)、鲸鱼算法(WOA)、二进制粒子群算法(binary particle swarm optimization algorithm，BPSO)以及TFMRFO算法分别在有无故障信息缺失或畸变时进行单重故障与多重故障配电网故障定位的仿真实验。本实验所构建的33节点配电网故障定位仿真拓扑模型如图3所示。

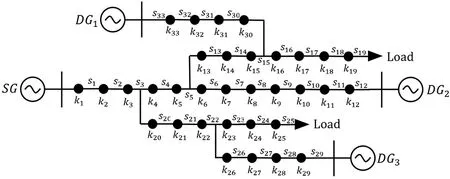
图3 33节点配电网仿真模型Fig.3 33-node distribution network simulation model

其中，系统主电源用SG表示，分布式电源用DG1～DG3表示，系统负荷用Load表示，开关节点与线路区段分别用k1～k33、s1～s33表示。

4.1 单重故障分析

随机选取6个区段做单重故障假设，系统电源与3个分布式电源均投入配电网系统运行。分别对每种算法在故障信息是否发生畸变的情况下循环运行50次，取正确定位次数所占总运行次数的比值来描述算法的准确性。系统只发生单重故障时的区段检测的结果如表1所示，其中区段s8、s21、s31发生单重故障时，节点信息均未发生畸变；区段s16、s5、s27发生单重故障时，节点I3、I22、I14发生信息畸变。

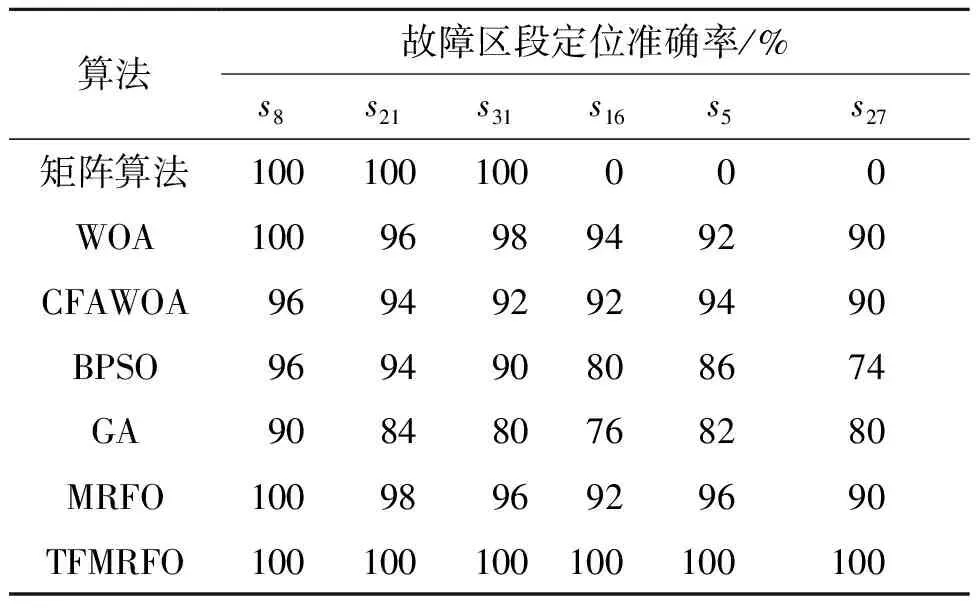
表1 单重故障定位结果

由表1可知，在配电网系统中只存在单个区段发生事故且无论故障信息是否完整的情况下，TFMRFO算法定位结果最理想，达到了100%的故障定位正确率。WOA算法、CFAWOA算法、MRFO算法有5%左右的可能性发生误判。BPSO算法的平均定位准确率为90%左右。GA算法的平均定位准确率为85%左右。在节点信息正常的情况下，矩阵算法才能正确定位出故障区段，否则，会直接发生错误定位。TFMRFO算法相比于MRFO算法而言，在系统发生节点信息不完整的状况下，定位准确率明显提升。

当s8发生单重故障时，在节点信息传输完整时，通过算法寻优运算可求得最小适应度值为0.5，输出结果向量为[000000010000000000000000000000000]，从而准确定位出s8发生单重故障，6种智能算法均完成了正确定位。其中，TFMRFO算法由于引入交流反馈机制，寻优前期适应度最接近全局最优值，从而最先完成故障定位。MRFO算法在两次迭代后达到全局最优，在单重故障状况下，通过算法收敛曲线尚未能明显地体现TFMRFO算法故障定位的优越性。算法收敛曲线如图4所示，F为算法求解所得适应度值，I为迭代次数。

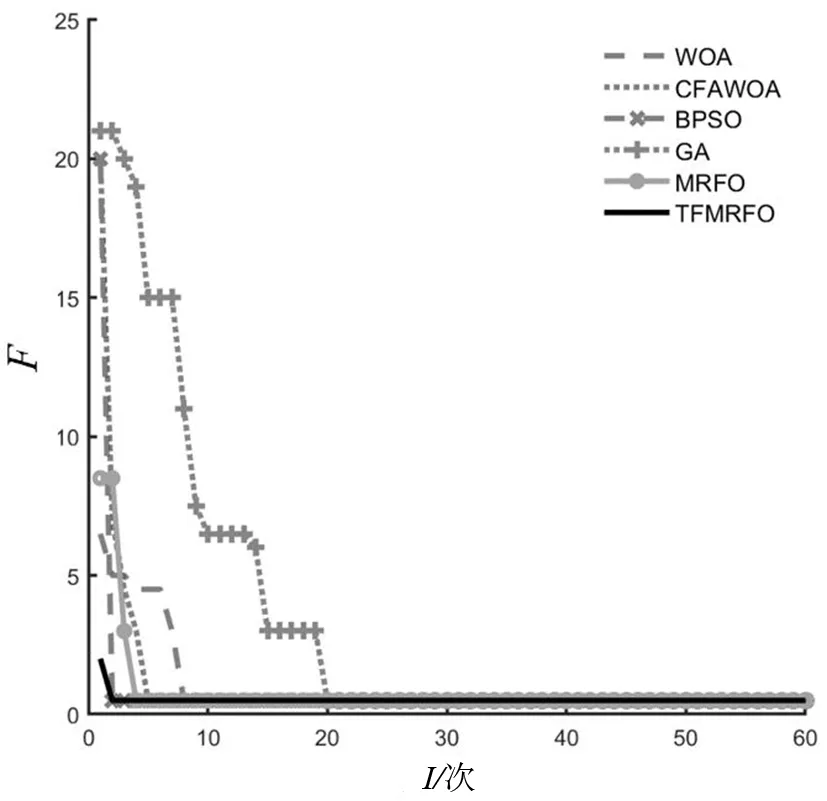
图4 无信息畸变单重故障定位收敛曲线图Fig.4 Convergence curve of single fault location without information distortion

当s16发生单重故障时，节点I3状态由“1”畸变为“0”，通过算法寻优运算可求得最小适应度值为1.5，算法收敛曲线如图5所示。输出结果向量为[000000000000000100000000000000000]，从而准确定位出s16发生单重故障。其中，TFMRFO算法最先完成故障定位，WOA算法次之，其他智能算法均出现了陷入局部极值状态。CFAWOA算法局部迭代时间过长，MRFO算法定位时间与TFMRFO算法时间相近，收敛速度快于BPSO算法，但前期出现了局部迭代、鲁棒性差、寻优性能不稳定等问题。大多数算法在伴随故障信息畸变的单重故障状况下均能准确实现故障定位，容错能力良好。只有GA算法在最大迭代次数内未能跳出局部最优状态，只求得局部极值，最终导致对故障区段做出误判。

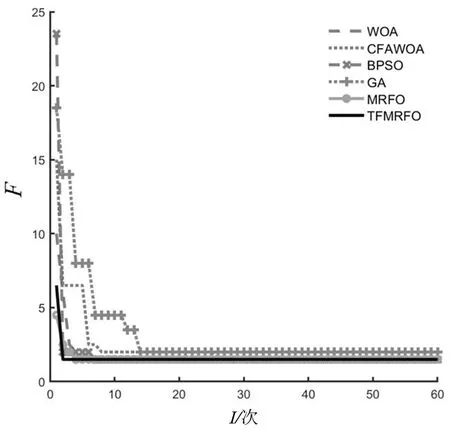
图5 信息畸变单重故障定位收敛曲线图Fig.5 Convergence curve of single fault location withinformation distortion

4.2 多重故障分析

随机选取多个区段做多重故障假设，其中包含多个开关节点信息发生畸变或缺失，系统中所有电源均正常运行。每种算法循环运行50次，记录每次实验结果，并对算法的故障定位准确性、容错性进行测试分析。发生多重故障时定位结果如表2所示，区段s6、s15，s23、s26发生多重故障时，节点信息均未发生畸变；区段s10、s22，s11、s28、s32发生多重故障时，节点I5、I7、I18、I24发生信息畸变。

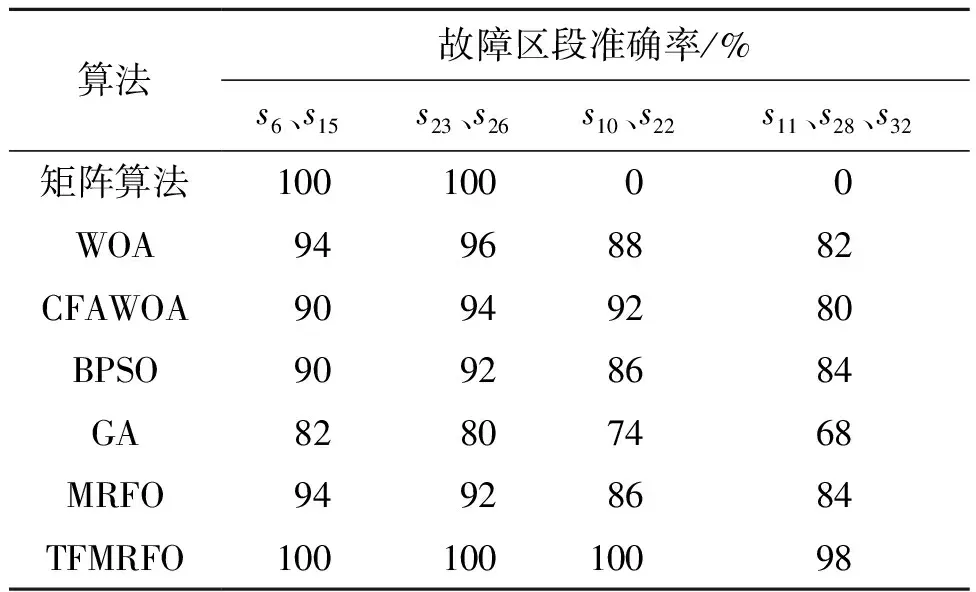
表2 多重故障定位结果

由表2可知，TFMRFO算法在配电网发生多重故障并且伴有故障信息存在畸变的情况下发生了一次误判，但定位准确率依然接近100%。WOA算法、CFAWOA算法、BPSO算法、MRFO算法有10%左右的可能性发生误判。GA算法的平均定位准确率为75%左右。当配电网系统中故障区段个数以及过流信息不完整的节点个数增加时，上述智能算法的故障定位准确率均随之下降。矩阵算法只有在节点信息保存完整的情况下，才能对多重故障能正确定位出故障区段，容错性能差，在FTU上传的节点信息发生遗漏或受损时不再适用。

当s6、s15发生多重故障并且节点状态未发生畸变时，通过算法寻优运算可求得最小适应度值为1，算法收敛曲线如图6所示。输出结果向量为[000001000000001000000000000000000]，从而准确定位出s6、s15发生多重故障。其中，TFMRFO算法最先完成故障定位，CFAWOA算法次之，其余算法均出现局部迭代状态。GA算法局部迭代耗时最严重，在第41迭代时才求得全局最优值。在发生多重故障情况下，TFMRFO算法较原始的MRFO算法改进效果更佳明显，未陷入局部最优状态，定位速率更快、精确度更高。

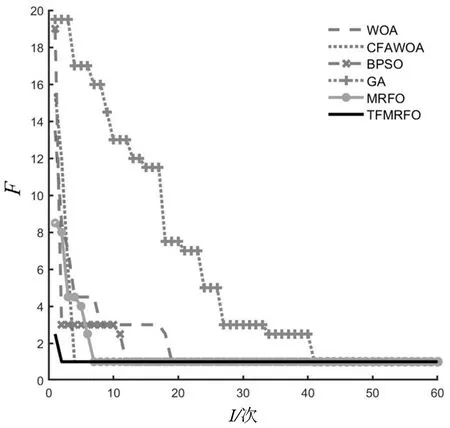
图6 无信息畸变多重故障定位收敛曲线图Fig.6 Convergence curve of multiple fault location without information distortion

当s11、s28、s32发生多重故障时，节点I7状态由“1”畸变为“0”，节点I24状态由“0”畸变为“-1”，通过算法寻优运算可求得最小适应度值为3，算法收敛曲线如图7所示。输出结果向量为[000000000010000000000000000100010]，从而准确定位出s11、s28、s32发生多重故障。其中，TFMRFO算法在第8次迭代时达到全局最优值，相对其他故障情况下故障定位速率下降，但在此故障类型下，相比于其他算法依然最先完成故障定位，而且寻优性能更加明显。TFMRFO算法在寻优过程中由于采用了Limit阈值的方法，陷入局部最佳状态的可能性被有效地避免了。通过群体间最优位置与最差位置的交流反馈，使得改进后的TFMRFO算法加强了全局搜索能力，加快了全局寻优速度。而原始的MRFO算法有3次陷入了局部极值状态，影响了解空间中全面求解的速度与精度。

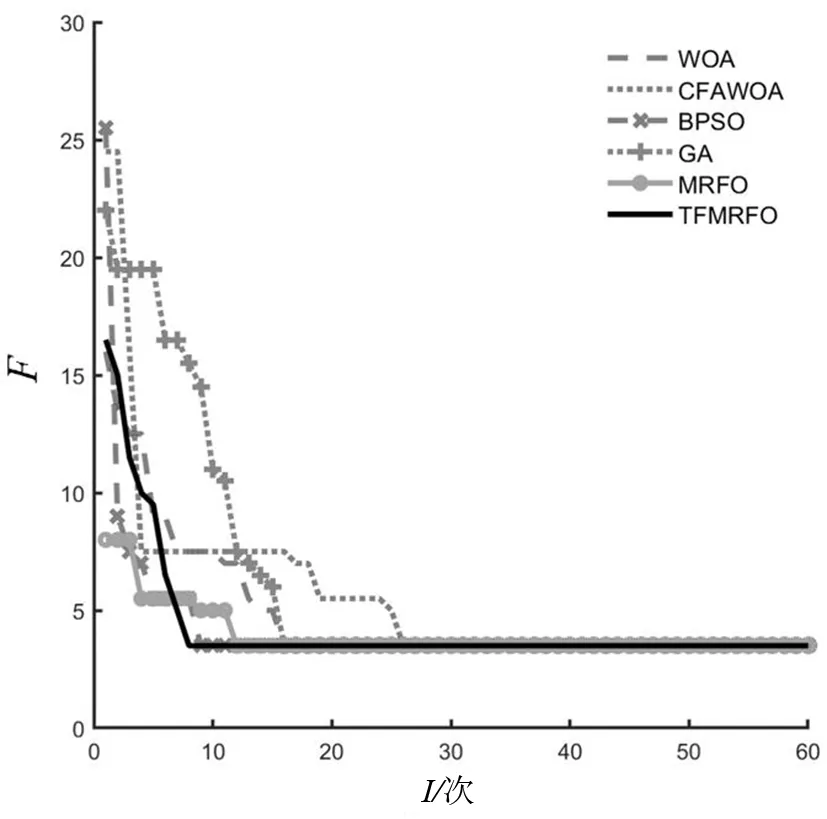
图7 信息畸变多重故障定位收敛曲线图Fig.7 Convergence curve of multiple fault location with information distortion

5 结论

本研究基于原始MRFO算法，引入了Limit阈值控制算法与信息交流反馈方法，提出基于TFMRFO的含DG的配电网系统检测故障的方法。该方法确立了在含DG的复杂配电网中节点开关的编码方式、开关函数以及适应度函数，利用TFMRFO搜索全局最小适应度值检测出配电网的故障区段的位置。应用Matlab构造出含DG的33节点配电网系统，基于TFMRFO算法在不同故障情况下模拟寻找配电网故障区段仿真实验。通过实验分析得出结论如下：

1)阈值Limit的合理设定，有效地改善了算法寻优过程中出现局部迭代状态的不足。算法求得局部极值时的迭代次数被减少，从而提高了算法计算精度和故障区段检测的准确率。

2)通过引入交流反馈机制，算法在全局的探索能力加强，鲁棒性得到优化，提高了算法的求解速度。多次实验仿真证明了收敛曲线波动小，性能稳定。

3)优化后的TFMRFO算法全局寻优能力与传统的智能算法相比，计算精度与收敛速度均得到改善，故障定位效率显著提高。

实验仿真过程中发现了TFMRFO算法在配电网发生多重故障且伴随故障信息发生畸变时，定位过程中陷入了局部最优状态。然而，实际生活中配电网同时发生多重故障的机率较小，因此基于智能算法的配电网故障定位更具有实际工程意义。在配电网规模不断扩大、结构愈加复杂的背景下，实现高效的配电网故障定位离不开对智能算法的不断优化改进。