基于RF的振动筛颗粒松散与分层分析

赵嘉乐，童昕,2，李占福，崔德海

(1.华侨大学 机电及自动化学院，福建 厦门 361021;2.福建工程学院 福建省数控装备产业研究院，福建 福州 350118;3.中建海峡建设发展有限公司，福建 福州 350000)

筛分机械广泛应用于煤矿开采、金属冶金、食品加工等行业，振动筛的筛分对象通常为散体物料，它由大量不同尺寸和形状的颗粒组成[1-2]。在筛分过程中，散体物料在筛网的作用下实现松散、分层、触筛和透筛的过程，达到物料分级的效果[3]。通过对筛分过程的研究，可以直观地分析筛上颗粒的运动与分布状态。

张恩来[4]采用密实度的定义量化了物料的松散情况，验证了物料松散是影响筛分效率的主要因素。Li等[5]对直线振动筛的松散进行研究，分析了松散系数、松散率与振动参数之间的关系。郭晟[6]采用颗粒粘结模型对物料的松散和分层进行研究，分析得到了组合振动筛振动参数对物料松散和分层的影响规律。黄志杰[7]基于分层细粒比的概念研究了入料速率对颗粒分层的影响。沈国浪[8]采用分层沉降系数来表征分层质量，并分析了振动参数对分层质量的影响。Davoodi A等[9]分析了颗粒密度和入料速率对物料分层和筛分效率的影响。

作为筛分过程的前期阶段，物料的松散和分层质量将会直接影响物料的触筛和透筛过程，进而影响最终的筛分效率。本文采用随机森林算法对筛机参数与物料的松散和分层进行数据建模，分析各筛机参数对物料松散指数和分层指数的影响权重及规律，并通过布谷鸟寻优算法进行双目标优化，寻求能同时满足较优松散质量和分层质量的参数组合。

1 模型建立与仿真实验设计

基于EDEM软件对直线振动筛的结构进行合理简化，仅保留了筛箱、筛网和入料口，如图1所示。

图1 振动筛简化模型Fig.1 Simplified model of vibration screen

选用球形颗粒作为筛分物料，采用直径均值分别为0.5 mm和1.0 mm的双峰正态曲线生成颗粒。实验设置共生成20 000个颗粒，入料速率为13 333颗/s，两种颗粒同时随机生成。

实验中材料属性及碰撞系数如表1和表2。直线振动筛具有多种可调参数，本文针对7种筛机参数进行研究，各参数的取值范围如表3。

表1 模型材料属性

表2 模型材料碰撞系数

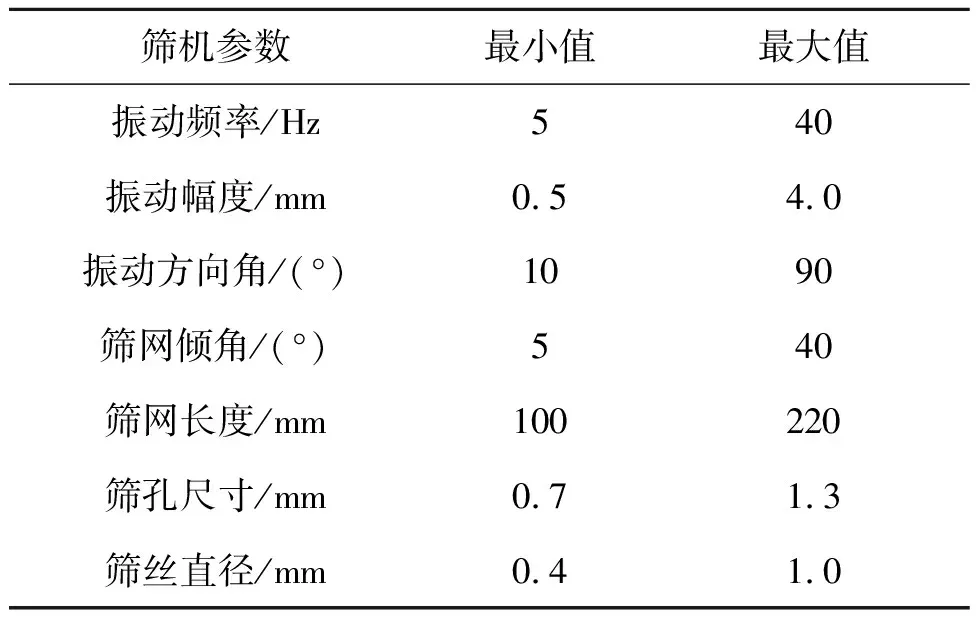
表3 筛机参数选取范围

2 颗粒的松散与分层

2.1 颗粒的松散

在筛分过程中，物料与筛网接触后被抛起，颗粒间距离增大，物料实现松散。物料的松散是整个筛分过程的前期阶段，松散质量在一定程度上影响颗粒分层、触筛和透筛的效果。本文采用密实度的定义来求取松散指数，即松散区域内颗粒总体积与该区域体积的百分比。松散区域上边界设置为颗粒质量占该区间段总质量的90 %，将下边界设置为颗粒质量占该区间段总质量的10 %。

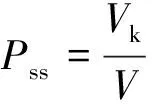
(1)

式中，Vk为松散区域内颗粒总体积，mm3；V为松散区域体积，mm3；Pss为松散指数。根据定义可知，松散指数越小，松散效果越好。松散指数随时间的变化规律如图2所示。

图2 松散指数随时间变化规律Fig.2 Looseness index changes with time

当筛网从平衡位置向上运动时，筛网不断挤压筛上颗粒，颗粒间距离减小，松散效果逐渐变差。当筛网从最高位置向下运动时，筛上颗粒与筛网接触碰撞后向上运动，颗粒间距离逐渐增大，松散指数逐渐减小至最小值。选取多个振动周期求取其松散指数的平均值表征该实验样本松散情况的优劣。

图3为松散指数和筛分效率的散点图，其皮尔逊相关系数为0.58，松散指数与筛分效率呈正相关关系。

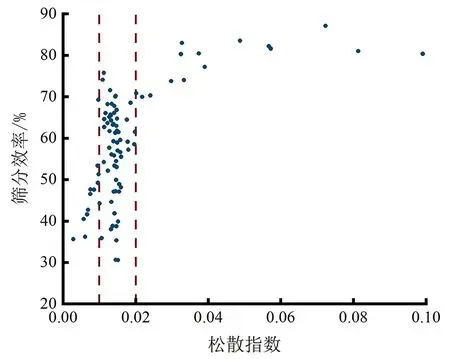
图3 松散指数与筛分效率散点图Fig.3 Scatter plot of looseness index and screening efficiency

图3中松散指数数值主要分布在0.01～0.02之间，所对应的筛分效率具有较大的偏差，说明不同的筛机参数组合将会导致相近的松散效果。当松散指数大于0.02，即松散效果较差时，筛分效率数值整体较高，其主要原因是颗粒在筛网上停留时间较长，其接触筛网的次数更多，成为筛下物的几率也越大，但完成筛分所需的时间较长。

2.2 颗粒的分层

筛分过程中，物料的松散和分层相互依存，颗粒与筛网接触后实现松散，颗粒下落过程中，小颗粒透过大颗粒间的间隙到达料层的底部，实现物料分层[10]。分层指数的具体定义为料层中小颗粒与料层中所有颗粒距离料层底层的平均高度的比值，料层底层边界为颗粒质量占该区间段总质量的5 %。当小颗粒与料层底层之间的距离小于所有颗粒与料层底层之间的距离时，即可认为小颗粒多集中于料层下方，是较为理想的分层效果。

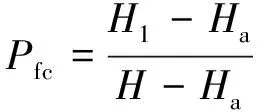
(2)

式中，H1为筛上颗粒中所有小颗粒距离筛网的平均高度，mm；Ha为料层底层距离筛网的高度，mm；H为筛上所有颗粒距离筛网的高度，mm；Pfc为分层指数。分层指数越小，分层效果越好。分层指数随时间的变化规律如图4所示。

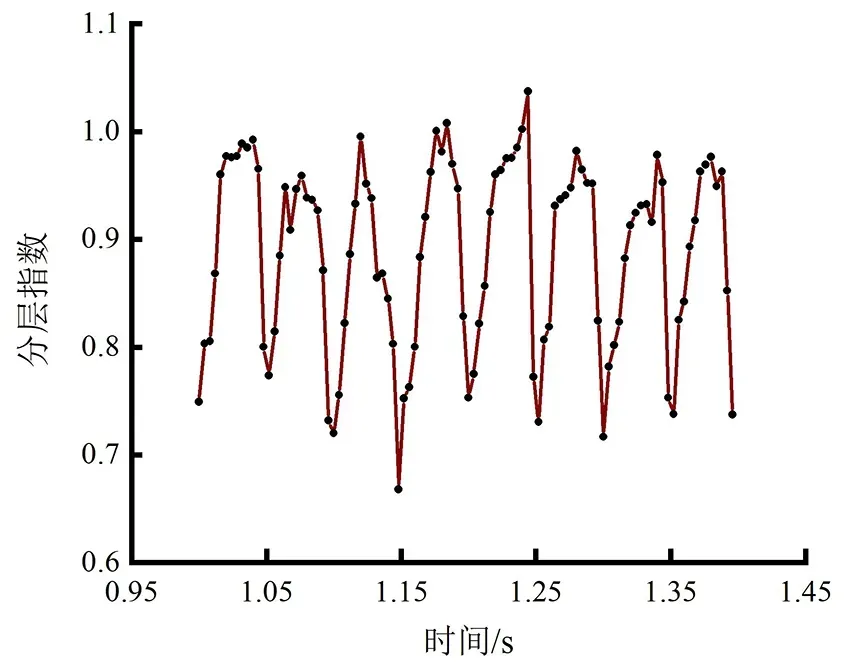
图4 分层指数随时间变化规律Fig.4 Stratification index changes with time

当筛网从平衡位置向上运动时，筛网不断挤压筛上颗粒，小颗粒与大颗粒混合，分层效果变差，分层指数逐渐增大。当筛网从最高位置向下运动时，筛上颗粒运动至最高点后开始下落，此时小颗粒将会透过大颗粒的间隙到达料层的底部，分层指数持续减小至最小值。选取多个振动周期求取其分层指数的平均值表征该实验样本的分层情况的优劣。

图5为分层指数和筛分效率的散点图，其皮尔逊相关系数为-0.53，分层指数与筛分效率呈负相关关系。

分层指数较小时，小颗粒更容易与筛网接触并实现透筛行为，筛分效率较大。由图5可知，分层指数的数值主要分布在0.95～1.05之间，即筛上颗粒并没有明显的分层现象。根据以往研究，物料中颗粒粒径分布较为离散时，更容易实现分层[11]。实验设置中入料颗粒采用双峰正态曲线生成，故筛上颗粒较难实现明显分层。

图5 分层指数与筛分效率的散点图Fig.5 Scatter plot of stratification index and screening efficiency

3 数据建模

3.1 随机森林算法

集成学习的基本原理是集成多个子模型，由每个子模型对数据进行分类判断，综合每个子模型的判断结果进行投票选择，最终做出判决，在每个子模型判断精度不高的情况下，最终决策也能达到较高的精度[12-13]。随机森林算法(random forest,简称RF)属于集成学习的一种，在数据分类和回归判断时采用决策树模型，随机森林算法不仅有着较高的预测准确度，且不易出现过拟合现象，模型的泛化能力较好，对异常值有着较好的容忍度。

3.2 松散指数的建模分析

采用随机森林算法建立7个筛机参数与松散指数的数据模型，进一步分析筛机参数对松散效果的影响规律及作用机理。筛机参数对松散指数的影响程度不同，利用集成学习的XGBoost(extreme gradient boosting)可以获取筛机参数对松散指数的影响权重[14]，分析结果如表4。

由表4可知振动频率、振动幅度和振动方向角对松散指数的影响权重较大，其影响规律如图6所示。

表4 筛机参数对松散指数的影响权重

由图6可知，松散指数随着振动频率、振动幅度和振动方向角的增大逐渐减小。振动频率和振动幅度的增大将会导致筛网在运动时具有更大的能量，筛上颗粒与筛网接触碰撞后将会被抛起至更高的位置，从而导致松散指数减小。振动方向角是筛网振动方向与筛网之间的夹角，当振动方向角较小时，颗粒与筛网碰撞后接触力的水平分力较大，竖直分力较小，颗粒在筛网的跳动幅度较小，松散指数较大。

图6 筛机参数对松散指数的影响Fig.6 Influence of vibration screen parameters on looseness index

3.3 分层指数的建模分析

同理对筛机参数和分层指数进行数据建模，得到筛机参数对分层指数的影响权重如表5所示。

表5 筛机参数对分层指数的影响权重

由表5可知，振动频率、振动幅度、振动方向角以及筛网长度对分层指数的影响权重较大，其影响规律如图7所示。

图7 筛机参数对分层指数的影响Fig.7 Influence of vibration screen parameters on stratification index

由图7(a)和图7(b)可知，随振动频率和振动幅度的增大，分层指数也增大。振动频率和振动幅度的增大使得小颗粒将会被抛送至较高的位置，其在下落过程中容易受其他颗粒的干扰，从而导致分层指数的增加，分层效果较差。由图7(c)可知，振动方向角在20°时取得较优值，之后随振动方向角的增大，分层指数也增大。较大的振动方向角将会导致颗粒与筛网碰撞后所受接触力的水平分力较小，颗粒间水平距离减少，小颗粒不容易透过大颗粒之间的间隙，因此当振动方向角增大时，筛上颗粒的分层效果变差，分层指数增大。

由图7(d)可知，在筛网长度小于120 mm时，随着筛网长度的增加，分层指数减小，当筛网长度大于120 mm后，随筛网长度的增加，分层指数则逐渐趋于稳定。因为在实验设置中，颗粒生成数量以及入料速率都是确定的数值，因此在筛机的振动频率、振动幅度、筛网倾角等参数确定后，即可认为振动筛具有一个稳定的处理能力，将小颗粒在筛网上完成筛分所经过的距离定义为筛网的有效利用长度，当筛网长度大于有效利用长度后，超出的部分则主要用于大颗粒的输送，对筛上颗粒的松散、分层几乎没有影响，所以当筛网长度大于一定数值后，分层指数则会趋于稳定。

4 参数优化

物料的松散和分层作为筛分过程的前期阶段，对筛分效率有较大的影响。由上述分析可知，振动参数对物料的松散和分层有不同的影响规律，通过筛机参数与松散指数和分层指数的数据模型，可以寻求合适的筛机参数组合以同时取得较优的松散质量和分层质量。

布谷鸟寻优算法(cuckoo search algorithm，简称CS)是剑桥大学YANG等提出的一种新型群智能优化算法，其基本思想是布谷鸟的巢寄生性和莱维飞行机制。布谷鸟算法具有参数较少、收敛速度对参数变化不敏感、全局搜索能力强、不易陷入局部最优解等优点[15-16]。布谷鸟算法的流程图如图8所示。

图8 布谷鸟寻优算法流程图Fig.8 Flowchart of cuckoo search algorithm

采用布谷鸟寻优算法对筛机参数进行双目标优化，寻求能够同时满足较优松散效果和分层效果的参数组合，即松散指数取得较大值，而分层指数取得较小值。将鸟巢位置设置为7维变量，对应不同的筛机参数，在算法迭代过程中，通过筛机参数与松散指数和分层指数的数据模型，将筛机参数转化为松散指数和分层指数。由于筛分过程中筛上颗粒并没有明显的分层现象，因此分别设置松散指数权重为0.7，分层指数的权重为0.3。确定优化目标函数为：

f=10lg(1+0.7Pss-0.3Pfc)

(3)

算法迭代效果如图9所示，寻优所得的筛机参数组合为：振动频率20 Hz，振动幅度2.5 mm，振动方向角18 °，筛网倾角18 °，筛网长度160 mm，筛孔尺寸1.0 mm，筛丝直径0.8 mm，此时，松散指数为0.032，分层指数为0.85。

图9 算法迭代过程Fig.9 Algorithmic iterative process

利用上述参数组合设置仿真实验，计算所得的松散指数为0.034，分层指数为0.83，筛分效率为80.6 %。算法寻优所得结果与仿真实验结果误差较小，且最终筛分效率值较高，验证了本文中模型建立与优化算法的准确性。

5 结论

1)物料的松散指数主要受振动参数影响，随振动参数增大，松散指数呈现减小趋势。物料的分层指数主要受振动参数与筛网长度影响，随振动频率和振动幅度增大，分层指数呈现增长趋势；随振动方向角增大，分层指数呈现先减小后增长的趋势，并在20°时取得最小值；筛网长度小于120 mm时，随筛网长度增加，分层指数减小，筛网长度大于120 mm时，分层指数则趋于稳定。

2)物料的松散指数主要分布在0.01～0.02之间，当松散指数大于0.02时，筛分效率数值整体较高且趋于稳定，但完成筛分所需时间较长。物料的分层指数主要分布在0.95～1.05之间，即筛上颗粒并未有明显的分层现象。

3)利用布谷鸟寻优算法对松散指数和分层指数进行双目标参数优化，得出最优的参数组合为：振动频率为20 Hz；振动幅度为2.5 mm；振动方向角为18 °；筛网倾角为18 °；筛网长度为160 mm；筛孔尺寸为1.0 mm；筛丝直径为0.8 mm。