LCL-S型无线电能传输系统负载与互感辨识方法

仇逸，汪凤翔，黄卫东，黄东晓

(1. 福建工程学院 机械与汽车工程学院，福建 福州 350118；2. 中国科学院海西研究院泉州装备制造研究中心，电机驱动与功率电子国家地方联合工程研究中心，福建 泉州 362000)

磁耦合谐振式无线电能传输(MCR-WPT)因其传输功率较大、传输距离较远、相对安全以及成本低等特性成为研究的热点[1]，被应用于电动汽车[2,3]、工业机器人[4]等诸多领域。随着无线电能传输技术的发展，传输功率小、系统损耗大、开关器件应力较大的问题使得单谐振拓扑无法满足系统性能的要求。而更为复杂的多谐振拓扑结构如LCL、LCC等由于拓扑的负载适应性更强、具有更大的谐振电容量等优势受到了青睐[5,6]。在无线充电系统使用中谐振器偏移、负载等变化等将使开环系统的性能降低甚至导致系统失控。为保证系统的高效传输，需要设计一种能够准确识别互感与负载的方法，提升系统模型精确度。

文献[7]提出了基于遗传算法考虑高次谐波的MCR-WPT系统负载和互感参数辨识算法。文献[8]提出基于谐波注入的基波谐波双通道并行的负载识别方法。文献[9]中提出了利用系统的状态方程同时引入粒子群算法进行参数辨识。文献[10]提出了基于MCR-WPT系统稳态模型参数辨识方法，仅需要对系统直流输入电压与直流输出电压进行采样，针对滤波电容能量守恒设计粒子群算法的边界条件，实现互感参数的辨识。文献[11]设计了一种基于参数识别的双面自整定LCC-S系统。文献[12]针对双向LCC补偿提出只需检测发射端电压电流实现负载大小的辨识。文献[13]提出基于副边可切换电容的方法，调整系统的工作状态，从而实现互感辨识。文献[14]提出基于粒子群算法的互感辨识方法，只需检测发射端电流即可。

上述对辨识方法的研究中，部分方法基于S-S谐振补偿拓扑，无法运用于多谐振拓扑中；部分方法的多谐振拓扑中没有针对LCL-S型拓扑，且无法进行多参数辨识。综上，本研究提出一种LCL-S型无线电能传输系统互感和负载辨识方法，建立系统稳态电路模型，设计粒子群算法，通过采样电压和预测电压等信息辨识系统实际参数。

1 系统原理与辨识方法设计

1.1 系统建模与分析

LCL-S型谐振电路的MCR-WPT系统拓扑兼具原边恒流、副边恒压的输出特性，如图1所示。系统整体由直流电源(Uin)、全桥逆变器(S1～S4)、谐振模块(Lp，Ls)、控制器、整流滤波模块和负载(RL)组成。发射端发出高频交流电产生的磁场，通过耦合线圈将能量传递到接收端，对负载进行供电。

图1 LCL-S型WPT系统电路图Fig.1 Circuit diagram of LCL-S system

Re为整流器后的等效负载，即

(1)

为了降低电源输入的无功功率以及提高系统能量传输能力，一般会使系统的激励频率与原副边固有频率相近。因此设计的系统电路参数选择满足以下条件。

(2)

1.2 系统建模及辨识方法

图1中输入的直流电经过全桥逆变过后，输出的方波用傅里叶级数展开过后可得：

(3)

由于LCL-S具有良好的低通滤波性，因此分析该拓扑时只需要分析基波分量即可，即：

(4)

根据互感原理，假定系统的工作频率为ω，可得系统的输入阻抗为：

(5)

由于系统工作频率为副边的谐振频率，因此反射阻抗为：

(6)

根据电路图结构、互感耦合定律及基尔霍夫定律可算得原副边的电流。

(7)

当系统处于固有谐振频率时，原边电流大小为：

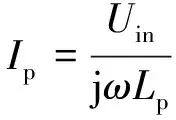
(8)

则输出电压为：

(9)

可以看出，LCL-S系统在谐振条件下，原边电流与副边输出电压与负载大小无关。因此原边可视为恒流源，副边可视为恒压源。

将输出与输入电压代入式(9)可算出互感，但经过多次测量与计算，该式算得的互感M与实际值有着较大的误差，如图2所示，当互感实际值为30 μH时，计算值约为31.79 μH，误差值为6.57%，误差较大。

图2 互感的公式计算结果与实际值对比Fig.2 Calculated mutual inductance value compared with the actual value

根据欧姆定律可算得原边线圈电压为：

ULp=Ip×|ZLp|

(10)

式中，Ip、ULp分别为原边线圈处电流、电压的有效值，|ZLp|为原边线圈处阻抗的模。

将式(6)、式(7)代入式(10)中，可推算出RL的表达式：

(11)

根据式(7)可推算出系统的负载输出功率为：

(12)

式中，

Y=(1-ω2LpCp)2+ω2Cp2Zr2

(13)

如图1所示，为了减少整流器输出的直流电的纹波，整流器后端使用滤波电容Cf。根据电容能量守恒公式可获得电容端电压和外部输入的能量的关系为：

(14)

其中，Vinital为初始时刻电压，Vfinal为结束时刻的电压，P为外部输入功率，T为持续时间。

将滤波电容公式(14)离散化，可得系统在kT时刻输出电压Uout(k)与(k+1)T时刻输出电压Uout(k+1)具有一下关系：

Uout(k+1)=

(15)

由于副边为恒压源，即RL的值大小对于输出电压没有影响，因此在使用式(15)做辨识时，可以先设负载RL为一个任意定值，可先辨识出互感值M，再将M代入式(11)中，将负载RL算出。

1.3 粒子群算法

粒子群优化算法(particle swarm optimization，PSO)源于对鸟群捕食的行为研究而得出的一种进化计算技术。

本研究基于粒子群算法提出一种LCL-S型WPT系统负载与互感辨识方法，通过粒子群寻优算法，建立系统稳态模型，并在相同的系统参数和输入条件下使其与实际系统性能达到最优拟合，从而实现参数辨识。主要分为两个步骤：

首先对粒子群初始化，包括粒子速度v与粒子位置x，其中x代表辨识值的变量，也就是互感M。第二步是进入迭代计算，在迭代过程中需要对v和x不断地更新，具体公式如下：

(16)

其中，k为惯性权重因子，kmax与kmin为权重系数的上限和下限；x(n)为当前迭代的次数；nmax为最大迭代次数，v(n)为粒子在第n次迭代的速度，x(n)为粒子在第n次迭代的位置，c1、c2为学习因子，random为0-1的随机数，zbest为个体最优，gbest(n)为全局最优。

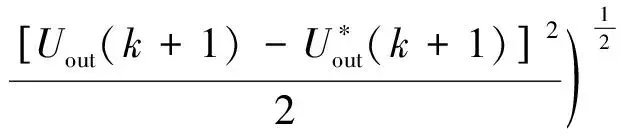
(17)

1.4 仿真

为了验证识别方法的有效性，在Matlab/Simulink仿真平台根据图1及上述的理论分析搭建相应的仿真模型，仿真时间设为2 ms，仿真步长设为0.1 μs。仿真参数按照实际系统的真实测量值进行设置，具体参数设置如表1所示。

表1 系统仿真及实验参数

由于负载的大小改变不会影响输出电压，因此在对M辨识时，可以将式(15)中的RL视作一个定值，设RL=15 Ω，通过该方式可以先将M值辨识出来。

在系统处于稳定时，即可按照粒子群算法流程对系统的互感与负载进行辨识。所辨识的互感值最大误差不超过2%，结果远好于式(9)的计算值。

在辨识出互感值之后，可以将辨识出的互感值代入式(11)中，将RL辨识出，表2列出互感M分别在20、30 μH，负载分别在20、30 Ω时的4种工况下的辨识结果。

表2 负载互感仿真辨识结果

图3 辨识值与实际值对比Fig.3 Identified value compared with the actual value

仿真结果表明，互感辨识误差较小，最大误差不超过2.00%；同时互感辨识是采用负载输出电压做辨识模型，而该拓扑副边可等效为恒压源，互感辨识不受负载变化影响。负载的辨识结果受互感变化影响较大，最大误差为5.35%，究其原因是互感发生变化时，系统最佳负载发生变化，原边线圈电压高次谐波含量增多，而系统模型仅考虑基波分量，因此会影响负载辨识精度。

2 实验

根据图1以及上述仿真分析搭建了LCL-S型WPT系统实验装置，系统参数由表1给出。全桥逆变电路选择GaN SYSTEM公司的GS61004B-EVBCD，逆变信号由函数信号发生器生成。识别算法在TI公司的LAUNCHXL-F28379D 中实现。

当实验系统负载RL为30 Ω、互感M为43.57 μH时，辨识结果如图4所示。

图4 部分实验结果Fig.4 Partial experimental results

在忽略噪声干扰后互感的辨识最大误差为3.90%，数值为42.59 μH，负载最大误差为5.70%，数值为31.72 Ω。通过切换负载以及调节线圈之间的相对位置以实现负载与互感的变化，进一步在不同的负载与互感条件下完成参数辨识，其辨识结果如图5所示。

图5 实验结果Fig.5 Experimental results

在实验中，互感的实际测量值分别为27.67、37.69、43.57 μH，负载分别为20、25、30 Ω，在同一互感下进行了3次负载变化辨识实验。其中负载辨识结果最大误差约为9.7%，最小误差为2.8%，互感最大辨识误差约为3.9%，最小误差为1.3%。由于实际电路和仿真参数有偏差，且存在采样误差，因此辨识出的参数相比于仿真误差更大。

3 结论

针对LCL-S拓扑多参数辨识问题，本研究提出了一种基于粒子群算法的互感与负载辨识方法，利用LCL-S拓扑恒压输出特性建立了输出电压的数学模型。基于该模型的准确性，向实际系统模型和数学模型输入相同数据，以判别两者输出状态变量的误差。该模型需要的系统采样点较少，信号采样方便。为了使辨识结果更准确，本研究引入粒子群算法，选取状态变量的差值作为其适应度函数，将传输系统的参数辨识问题转换为最优解问题，完成参数辨识随后通过系统原边线圈恒流特性计算出负载大小。实验通过调整谐振线圈之间的距离和负载电阻来改变互感与负载的大小，在DSP28379中实现在线辨识。

仿真与实验结果均表明，基于粒子群算法的负载、互感辨识方法模型简单、易于实现且可以同时以较高精度辨识出互感和负载，且无需增加额外硬件电路及控制，降低了系统复杂程度。