聚焦数学阅读 演绎别样精彩

戚立辉

(江苏省兴化中学，225700)

《普通高中数学课程标准》指出:“高中数学课程体现社会发展的需求、数学学科的特征和学生的认知规律,发展学生数学学科核心素养．……强调数学与生活以及其他学科的联系,提升学生应用数学解决实际问题的能力,同时注重数学文化的渗透．”并要求“不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值．”这使得高考数学试题由单纯地对数学文化的考查演变为对在各种情境下数学阅读的考查.本文结合几道高考试题,对此进行思考．

一、数学阅读与建筑情境相结合

(1)求四棱锥的总曲率;

(2)若多面体满足:顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数.

解(1)由题可知:四棱锥的总曲率等于四棱锥各顶点的曲率之和.可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.易知四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,则其总曲率为2π×5-(4π+2π)=4π.

(2)设顶点数、棱数、面数分别为n，l，m,所以有n-l+m=2.设第i个面的棱数为xi,所以x1+x2+…+xm=2l.因而总曲率为2πn-π[(x1-2)+(x2-2)+…+(xm-2)]=2πn-π(2l-2m)=2π(n-l+m)=4π.故这类多面体的总曲率是常数.

评注本题考查立体几何的新定义问题,能够正确读懂“曲率”的概念是解决问题的关键.同时也让学生在解决数学问题之余体会现代建筑之美,感悟数学的审美价值.

例2攒尖是古代中国建筑中屋顶的一种结构形式，宋代称为撮尖,清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.也有单檐和重檐之分.多见于亭阁式建筑,园林建筑.以八角攒尖为例(如图2),它的主要部分的轮廓可近似看作一个正八棱锥,若此正八棱锥的侧面等腰三角形的底角为α,则侧棱与底面外接圆半径的比为( )

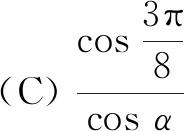
评注本题以中国古典建筑为问题情境,考查了数学阅读的能力,以及空间问题角的实际运用,考查空间想象能力．

二、数学阅读与中外数学史情境相结合

例3我国南北朝时期的数学家祖暅在计算球的体积时,提出了一个原理(祖暅原理):“幂势既同,则积不容异”.这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差.图4是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以1为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD.用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形.模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图5),从而求得该帐篷的体积为( )

评注本题以课本阅读部分的中国古代著名数学家祖暅提出的“祖暅原理”为问题情境,考查空间几何体的体积,以及空间想象能力,激发考生的民族自豪感.

例4康威圆定理是英国数学家约翰·康威引以为傲的研究成果之一.定理的内容是这样的:如图6,∆ABC的三条边长分别为BC=a,AC=b,AB=c.延长线段CA至点A1,使得AA1=a,以此类推得到点A2,B1,B2,C1和C2,那么这六个点共圆,这个圆称为康威圆.已知a=4,b=3,c=5,则由∆ABC生成的康威圆的半径为______.

解法2以C为原点,CA所在直线为x轴,CB所在直线为y轴,建立如图7所示的平面直角坐标系,则A1(7, 0),B1(0, 7),C1(0,-5),C1(-5, 0).

设康威圆的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),把A1(7, 0),B1(0, 7),C1(0,-5)代入圆的方程,得

评注本题以“康威圆定理”为情境考查直线与圆的相关知识,考生既可以用平面几何知识解题,也可以用解析几何的知识求解,并且要求考生在进行认真、仔细的数学阅读后需要抓住问题的本质才能够解决问题.

三、数学阅读与现代科学情境相结合

例5新型冠状病毒肺炎(COVID-19)疫情爆发以来,中国人民万众一心,取得了抗疫斗争的初步胜利.面对秋冬季新冠肺炎疫情反弹风险,某地防疫防控部门决定进行全面入户排查,过程中排查到一户5口之家被确认为新冠肺炎密切接触者,按要求进一步对该5名成员逐一进行核酸检测.若任一成员出现阳性,则该家庭定义为“感染高危户”.设该家庭每个成员检测呈阳性相互独立,且概率均为p(0

评注本题以新冠疫情的核酸检测为数学阅读情境,了解核酸检测的原理,感受疫情防控的刻不容缓和工作人员的辛苦,体会数学在现代科学中的应用价值.

四、数学阅读与其他学科情境相结合

例6 将地球近似看作球体.设地球表面某地正午太阳高度角为θ,δ为此时太阳直射纬度(当地夏半年取正值,冬半年取负值),φ为该地的纬度值,如图8.已知太阳每年直射范围在南北回归线之间,即δ∈[-23°26′,23°26′].北京天安门广场的汉白玉华表高为9.57米,北京天安门广场的纬度为北纬39°54′27″,若某天的正午时刻,测得华表的影长恰好为9.57米,则该天的太阳直射纬度为( )

(A)北纬5°5′27″ (B)南纬5°5′27″

(C)北纬5°5′33″ (D)南纬5°5′33″

解由题意可知,天安门广场的太阳高度角θ=90°-(39°54′27″-δ)=50°5′33″+δ,由华表的高和影长相等可知θ=45°,所以δ=45°-50°5′33″=-5°5′33″.所以该天太阳直射纬度为南纬5°5′33″,故选D.

评注在许多考生的印象中地理偏向于文科学科,本题就体现了数学在地理学科中的应用,考查考生的空间想象能力和数学理解能力.

国家提出以真情实景落实“五育并举”、以理性思维践行“立德树人”的命题指导思想,对学生的数学阅读能力提出了极高的要求．原江苏卷阅读量约1 200字,新高考Ⅰ卷的阅读量约1 900字,阅读量显著增大．新教材无论是苏教版还是人教版都增加了大量的数学阅读材料,是实施数学阅读教学的非常重要的教学资源,所以在平常的教学中，要注重渗透数学阅读的教学,切实提高学生的数学理解能力,将情境转化为熟悉的数学问题,体现数学的应用价值．