思维障碍成因剖析与教学对策

陈应全 王胜峰

(广东省茂名市广东高州中学,525200) (广东省广州市培英中学,510400)

数学思维是针对数学活动而言的,通过对数学问题的提出、分析、解决、应用与推广等一系列工作,以获得对数学对象(空间形式、数量关系、结构模式)的本质和规律的认识.这一过程使人脑的意识对数学对象信息的接受、分析、选择、加工与整合[1].解题则是训练数学思维的重要途径之一.本文对解题思维障碍的成因以及突破解题思维障碍的教学对策，进行探究.

一、解题思维障碍成因剖析

1. 缺乏解题策略指引

数学解题策略主要是指解题的综合能力,它包括审题能力、如何筛选方法的能力、转化能力、综合运用知识的能力等[2].数学解题策略不是单纯的解题方法,也不是普通的归纳小结.如在立体几何证明中常常用“顺逆推策略”,即由求证想判定,由已知想性质.在三角化简中常常用“差异分析策略”,即化简讲究角、函数名称与结构的“统一性”等.在解题过程中,学生往往缺乏解题策略的指引，导致无法找到准确的解题思路而出现解题思维障碍.

2.深陷思维定势影响

思维定势又称“习惯性思维”,是指人们按习惯的、比较固定的思路去思考问题、分析问题,表现在解决问题过程中作固定的方式准备.新高考高度关注与创新密切相关的能力和素养,注重考查学生探索新方法、积极主动解决问题的能力,鼓励学生摆脱思维定势的束缚,勇于大胆创新[3].因此,近年来很多高考题和模拟题纷纷出现了不少新情境、新信息与新定义等好题,要求学生随机应变地调整解题思路，方能顺利解答.这也预示着思维定势严重的学生在解这类题时往往出现思维障碍.

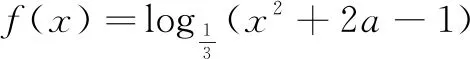
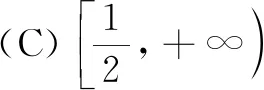
分析学生在做这类值域问题时,常常由于思维定势而错选D,归根结底是学生先入为主地认为值域为R时,其定义域也为R.

在解题教学中,特别当新问题与旧问题形似质异的时候,思维定势往往会促使学生步入误区,这也使得他们出现解题思路中断或者出现错解等现象.思维定势的形成主要是“灌输式”教学方式或者“不求甚解”的学习方式造成的.

3.解题心理负担过重

新高考评价体系中“四翼”十分注重考查主干知识的综合性、应用性与创新性,通过设置真实的问题情境,考查学生灵活运用所学知识分析解决问题的能力[3].因此在高考中常常有不少考题思维跨度较大,解题过程复杂和具有适度的创新性，这些因素容易给学生造成比较重的心理负担,往往导致他们解题思维出现障碍,望题兴叹.

(A)346 (B)373

(C)446 (D)473

分析本题以三角高程测量法测量珠峰高程为背景,考查正弦定理的应用.此题关键是正确将AA′-CC′的长度通过作辅助线的方式转化为相关线段的长度即可(如图2).但是由于题目边与角关系众多,不少考生在短时间内未能理清它们间的关系,使他们心理负担过重而出现思维障碍.

由此可见，学生解题心理负担过重的原因是多方面的:一方面是高中数学内容较多,考查难度较大；另一方面是学生在数学学习中虽然花了比较多时间,但是由于诸多因素影响，导致成绩不尽如人意,使得他们学习数学的信心不足.此外,部分学生功利性太强,急功近利也是造成心理压力过大的原因之一.因此学生保持平常心对释放解题心理压力显得异常重要.

4.相关概念理解不透

数学概念是数学命题、数学推理的基础部分,也是数学逻辑思维的最基本的逻辑思维形式.在解题教学中,有部分学生对数学概念的发生、发展过程理解得不够透彻,仅仅停留在了解、知道的水平上.因此，当学生在解题中需要运用用相关概念解题时,思维往往会模糊不清,从而产生解题思维障碍.

例5已知函数f(x)的定义域为R,f(x+2)为偶函数,f(2x+1)为奇函数,则( )

(C)f(2)=0 (D)f(4)=0

分析解这道题时,很多学生对函数奇偶性概念理解得不透彻，对于复合函数错误地将含自变量的代数式当成自变量,得到如下错误的解答过程:由f(x+2)为偶函数得到f(-x-2)=f(x+2),由f(2x+1)为奇函数得到f(-2x-1)=-f(2x+1),至此而未能求出f(x)的周期，导致思路受阻.

学生对概念理解不透彻，与教师的教学理念有非常大的关系.由于受应试教育的影响,很多老师在数学教学中重解题、轻概念,片面地认为概念只要求学生记忆即可,这样造成解题与数学概念严重脱节的现象，在高中数学课堂中相当普遍.

5.忽视隐含条件

已知条件是解题的前提,但是有些条件没有明确表达出来的,而是巧妙地隐藏在题目中,不少学生在解题中往往忽视对这些隐含条件的挖掘,以致未能清晰地找到条件与结论之间的连接点，从而陷于难以应对的困境,解题思维出现障碍.

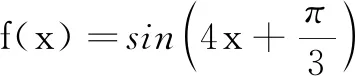
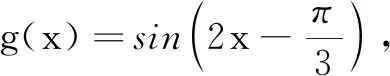
二、 教学对策

1.坚持素养先行

新高考评价体系创造性地提出“价值引领、素养导向、能力为重、知识为基”的高考评价新理念, 通过整合以往必考内容和选考内容,将核心素养自然融入.在新高考试题命制层面,进一步强调情境化设计,推动核心素养在教学和考试中的落实[3].因此,受新高考的引领作用,教学应以发展学生数学学科核心素养为导向,引导学生把握数学的本质.从上述解题思维障碍成因分析可知,学生之所以在解题时出现思维障碍，实质上是学生思维能力有所欠缺,归根结底就是数学素养不足.如例1,学生出现思维障碍主要是由于数学运算素养欠佳,表现在对探究运算路径与选择运算方法上不尽如人意;例2主要问题在于直观想象素养不足,表现在学生未能很好地建立数与形的联系,在具体数学情境中未能形成较好的数学直观.所以，在解题教学中,教师应该坚持素养先行的教学理念,重视解题思路的探索过程,实现由“问题导向”到“素养形成”的转变,便于学生形成科学合理的思维模式与方法,这对学生在解题中如何运用合理的思维模式思考数学问题意义重大.

2.注重例题选取

新高考评价体系指出:高考注重对基本思想方法的考查,立足通性通法,淡化解题技巧,杜绝偏题、怪题和繁难试题[3].这也预示着在解题教学中要立足通性通法.通过选取典型例题,加强对通性通法的训练并落实“四基”,注重通性通法的解题教学常常会经历“概括、推理、比较、分析、综合与归纳”等思维活动,此举既能加深学生对数学公式、概念的理解，又能提高思维能力.其次,在解题教学中,要充分考虑学生的学情,选取难度适中的试题作为例题，以有利于教学的开展与教学目标的达成,这样的教学有助于提高学生学习数学的兴趣与信心,有助于缓解学生过大的心理负担,从而有利于预防学生思维障碍的发生.

3.重视思维呈现

数学学习就是学习如何思考,培养学生思维能力应该是数学课堂中重要的目标之一.因此，在解题教学中,除了不能忽视引导学生进行思考,还要注重诱导学生暴露他们的思维过程(包括例证、推论与结论等),让他们的思维习惯、思维痛点与语言表达习惯得以呈现,及时抓住时机细心诊断学生思维过程,并根据他们的具体情况采取有效措施，纠正存在的不良的思维习惯.此外,也可以精心设计具有诊断性的题目,引导学生思考,让他们的错误观点暴露之后,通过集体讨论后给予指正,这样的教学给学生留下的印象是深刻的.在解题教学中,重视学生思维的呈现并给予及时纠正，对突破他们解题思维障碍是一条有效的路径.

4.强化策略指引

解题策略是对学生解题较高层次的要求,不仅要求会解,还要求如何解得简单、快捷,这样可使学生面对解题时变得更加轻松、从容,做到以不变应万变.因此,在解题教学中，应把重点放在解题策略的引导上,避免学生一拿到题目就做,应引导他们思考这种方法如何想到,还可以有哪些应用等.要把以往枯燥的、机械的讲解变成学生主动的、探究的生成,要找出偶然之中的必然[2],让学生感觉到每一种解法都不是从天而降,而是自然生成的.这样的解题教学，可使学生领悟到各种解题方法的精髓后便能形成自己的解题策略,从而有效减少解题思维障碍的产生.