学习进阶视角下的数学课堂教学研究
——以“平面图形中的数量积问题”教学为例
2022-06-23袁锁盘
袁锁盘
(江苏省梅村高级中学,214000)
所谓学习进阶是指随着时间的推移,学生对某一知识内容的认识不断丰富、精进和深入的过程.学习进阶在国际上的影响十分广泛,它最先应用于科学研究.近些年来,随着学习进阶理论的发展:数学教育界也开始重视起这一重要理论.在学习进阶理论的指导下,要清楚学生应该先学什么,后学什么,先学的内容要能够为后面所学的内容打好基础.
《普通高中数学课程标准》(2020年修订)在课程目标中提出“四基”、“四能”的要求[1].学习进阶理论正是反映了学生在数学学习过程中如何由基本的“四基”,“四能”发展到数学学科的核心素养,进而最后提升学生在数学学习中的实践创新意识,提升学生感受数学的文化价值与审美价值[2].
本文以高三一轮复习中的“平面图形中的数量积问题”专题课为例,依据学习进阶理论,探讨如何运用学习进阶理论进行课堂教学设计与实践.
一、进阶目标设计
(1)利用平面图形中向量的线性表示引出向量的数量积运算,体会向量的数量积与向量线性表示间的联系;
(2)理解并掌握平面图形中求数量积的一些方法;
(3)通过数量积方法的深入探究,掌握求数量积的一些技巧,从而能够快速精准地解决一些选择题和填空题;
(4)在探究过程中通过归纳、推理的数学思想,将数量积与解三角形、基本不等式、解析几何等其他数学知识联系起来,进行拓展延伸.
二、课堂教学活动设计
进阶目标掌握求数量积的一些方法以及技巧;会选择合适的方法与技巧解决数量积问题;数量积与一些其他数学知识融合问题的灵活解决.
进阶层级1理解并掌握求数量积的方法


解寻找封闭图形线性表示(过程略).

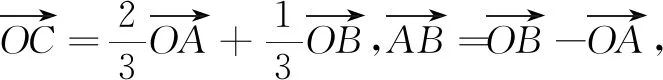



设计意图从教材上的一道习题出发,虽然难度不大,但恰恰达到一种循序渐进的教学效果,然后在此基础上进行改编.改编后的题目紧扣本节课的重点内容,让学生尝试多种方法求数量积.最后让学生自己进行总结,从而使学生对于求数量积的最常见的几种方法能够熟悉掌握.
进阶层级2理解并掌握极化恒等式的三角形模式这一求数量积的技巧
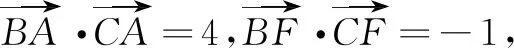


设计意图本题是2016年江苏卷填空题第13题,属于难题,学生在解决此题时错误率比较高.究其原因,主要是学生对于求数量积的方法不熟练,不能找到合适的基底,并且此题建系,利用坐标法比较困难,需要利用平面几何的知识求点坐标.在此基础上,因势利导介绍解决数量积问题的一个技巧——极化恒等式,并与学生共同探讨在什么情况下可以想到极化恒等式,帮助学生总结以下规律:(1)两个向量要有一个公共起点;(2)要想到在三角形一边上取中点.
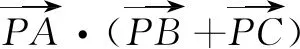
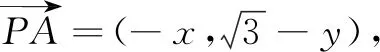

设计意图本题选取2017年全国卷中的一道题作为变式,如果运用极化恒等式非常容易解决.这样,学生在掌握求数量积的几种常规方法后又在此基础上进阶一个层级,能够熟练运用极化恒等式这一技巧来解决一些填空题、选择题.
进阶层级3求数量积方法以及技巧在解题中的选择

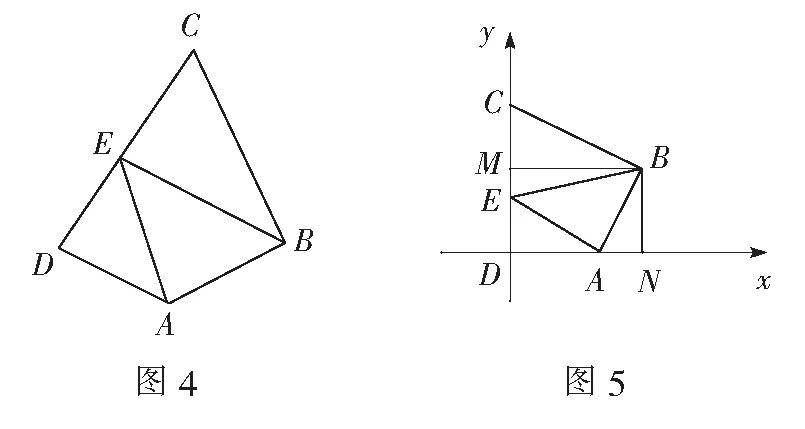
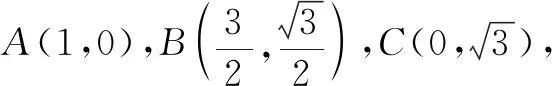
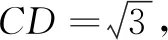

设计意图主要是让学生体会如何选择最佳方法解决数量积问题.
另外,为确保调查研究的真实、有效、客观、全面,本课题组成员奔赴体校,并对部分运动员、教育管理人员等就文化教育的现状、管理等问题进行了实地调研和访谈。
进阶层级4数量积与其他数学知识的融合,逐步提升学生的应用能力


设计意图这两个思考题是在例3的基础上提出来的,主要目的是与解三角形、基本不等式进行融合.如果已经复习解析几何,可以尝试将数量积与解析几何进行融合.在这两个思考题之后,学生在数量积的学习中再次进阶一个层级,即体会数量积与解三角形、基本不等式等其他数学知识的融合,能够在很多平面图形的问题中灵活运用数量积的方法求解问题,应用能力得以提升.
三、几点建议
1.了解学生的认知发展,抓住一轮复习的进阶起点
高三一轮复习仍应以基础知识为主,在一轮复习中一定要让学生把基础题练透,练扎实,切勿盲目增加难度.虽然学生已经在高一、高二把内容学完了,但是在实际教学中可以发现学生的遗忘性很大,对于参考书上的很多习题无法解决,究其原因还是对于知识的本质缺乏深入理解,因此在教学中仍应回归教材,充分利用好教材上的题目,并以此为进阶起点,在学生已有知识经验的基础上逐层进阶.
2.在讲解题目时要掌握进阶维度,提升一题多变的效果
高三很多教师在讲解题目时喜欢对某一题进行变式,这是一种很好的讲解方法.但是很多教师不注重变式题目的质量,有时变式并没有多大意义.因此,在平时的教学中应沉下心来,多钻研一些新题,好题,并敢于尝试将这些习题与本节课的知识点融合贯通起来,题目的变式既要在原题上提升难度,又不能超越学生当前的认知范畴,要结合学生的实际情况进行选题变式,切忌整个年级“一刀切”.
3.教学中要适时反馈,关注学生学习中的进阶终点
高三每隔一段时间都会进行一些检测,然而很多教师仅仅关注学生的成绩,只关心学生这一段时间是进步还是退步,对于学生知识的掌握情况知之甚少.其实对于每一次的检测更要关注学生知识点的掌握情况.例如可以对学生某一知识点进行“跟踪式”评价,刚开始可以给学生选择相应知识点的题目进行练习,并不断在此基础上加深难度,但最关键的是后期要对学生的掌握情况进行及时评价,关注学生在这一知识点的进阶终点有没有达成.
