离心通风机叶轮失速的混沌特征分析*
2022-06-23孟凡念张子琦王良文
孟凡念,张子琦,王良文
(郑州轻工业大学机电工程学院∕∕河南省机械装备智能制造重点实验室,郑州 450002)
0 引言
离心通风机在煤矿通风中非常重要;另外,在矿山、建筑、能源、化工和航天等领域运用广泛,对其性能进行研究对于节能减排和保护环境意义重大。小流量工况下运转时,离心通风机会出现诸如二次流、涡流、失速和喘振等不稳定现象,进而能够增加离心通风机的流动损失,影响其运转效率和可靠性。其中旋转失速和喘振是影响离心通风机不稳定运行的主要因素。
在叶轮失速的研究方面,肖美娜[1]对双吸式离心通风机的旋转失速机理进行研究,采用数值模拟和试验研究两种方法分析了对离心通风机的定常流动和非定常流动,讨论了旋转失速现象产生和发展的过程。刘震雄等[2]应用本征正交分解方法对压气机失速过程中叶顶流场进行研究,研究结果表明:失速过程起始于叶片顶部区域,并逐渐发展为失速团。皮骏等[3]应用熵学理论并结合CFX 软件对NASA Rotor37 压气机模型的稳定状态到失速和喘振状态进行数值模拟,为失速和喘振下的故障诊断提供指导。周佩剑等[4]采用大涡模拟研究了离心泵的压力脉动信号。喻伯平等[5]建立了基于动网格技术和代理模型的Kriging 代理模型动态失速特性优化方法。赵振宙等[6]在分离涡模拟和k-ωSST模拟技术下分析了涡流发生器对动态失速的影响。李亮等[7]研究了扫路车用风机内部湍流的数值模拟技术,试验与仿真结果的对比分析验证了方法的合理性。另外,Mauro Righi等[8]研究了轴向流动压缩机内部三维流动的旋转失速和喘振现象。Elias Sundstrom等[9]和Mohammad Ali Azizi等[10]对离心压缩机内的失速机理进行了探索。张亚等[11]研究了轴流风机喘振现象。
本文在对某型离心通风机不定常流动CFD 数值模拟的基础上,得到叶轮出口处旋转失速下的压力时间波动值,并对该数据序列进行相空间重构、最大Lyapunov 指数和关联维数分析等非线性混沌特性分析,旋转失速下混沌特征的分析为工程上识别旋转失速提供了一定的工程指导意义。
1 计算模型
主要对9-19.4A 型离心通风机的旋转失速进行研究,该型离心通风机的结构如图1所示。

图1 9-19.4A型通风机结构Fig.1 9-19.4A type centrifugal fan structure
2 CFD数值模拟
2.1 仿真模型及网格划分
离心通风机的主要构件为叶轮、蜗壳和进气口,这3 个构件在三维软件PROE 中建模后另存为*.x-t 格式文件,并把该文件导入到软件ICEM 中划分网格,计算域在蜗壳和集流器出口处进行了延伸,这样模拟能准确。在划分网格时,蜗壳和叶轮由于结构比较复杂而划分为非结构化四面体网格,把集流器中建立拓扑结构进而划分为六面体网格,并进行了网格无关性试算。划分后的网格如图2所示。

图2 划分后的网格Fig.2 the grid after divided
2.2 数值模拟
进气口延伸处为进口域,总温为293 K,总压为标准大气压101 325 Pa 为进口边界条件,蜗壳延展处为出口域,质量流量为出口边界条件。失速喘振流动仿真时以稳态流动仿真结果作为初始条件,正常工况下出口流量为0.421 3 kg∕s时仿真结果的压力云图如图3所示。
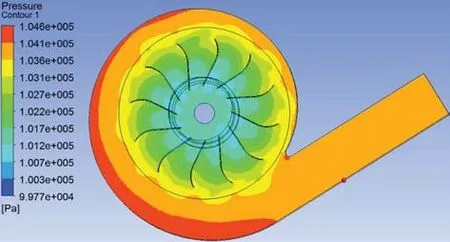
图3 正常工况下的压力云图Fig.3 Pressure chart under normal working condition
当出口流量减小到0.1 kg∕s时,失速后的压力云图如图4所示。

图4 失速后的压力云图Fig.4 Pressure chart after stall
由图3~4 可以看出,失速下的压力高于正常工况下的压力,失速下的蜗壳出口处形成局部高压区,此时叶轮已经处在失速工况。
由于离心通风机旋转失速后流场具有非线性特征,在此通过一组采集点的压力输出时间数据序列进行研究,通过相空间重构挖掘出系统内的复杂的动力学特征,压力采集点如图5所示。通过非定常数值模拟来得到采集点随时间变化的压力时间数据序列,并以此数据序列为非线性混沌动力学分析的基础。

图5 压力采集点Fig.5 Pressure acquisition point
压力采集点处的压力时间数据序列如图6所示。

图6 采集点处的压力时间数据序列Fig.6 Pressure time series at acquisition point
3 压力时间数据序列的混沌分析
上面采集到的压力时间数据序列作为混沌分析的基础,在此进行混沌分析,主要通过相图法、Lyapunov指数判断法和关联维数法进行压力时间数据序列的混沌识别。
3.1 相图法
通过相空间重构,一维数据序列能够映射到高维空间中,根据Takens 等学者的理论,一维数据序列与重构后的高维空间微分同胚。通过重构压力时间序列的相空间来定性的判断混沌性,这就是相图法。
对失速状态下叶轮处压力时间数据序列进行相空间重构后,二维相图和三维相图如图7 所示。由图可知,二维相图在有限的区域内具有一定的聚集性,三维相图同样具有一定的规律性,近似椭圆的形状,可根据其规律性推断奇异吸引子的存在。因此,失速状态下叶轮处压力时间数据序列具有混沌特性。

图7 二维相图和三维相图Fig.7 2D and 3D phase diagrams
3.2 Lyapunov指数法
最大Lyapunov指数用小数据量法获得,具体步骤如下。
(1)压力数据序列{x(i)i= 1,2,…,N}的快速傅里叶变换,确定平均周期P。
(2)用自相关函数法计算出延迟时间τ,Cao 法计算出嵌入维数,并重构相空间,即:

式中:M为相空间的点数;m为嵌入维数;τ为延迟时间,且M=N-(m- 1)τ。
(3)点X(j)的最邻近点X(ĵ)计算,并限制短暂分离,即:
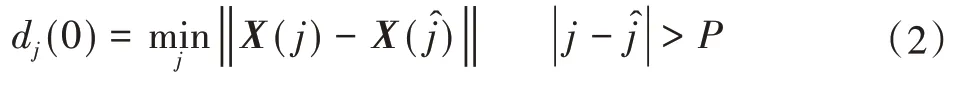
(4)对每个点Xj,计算出该邻点对的i个离散时间步后的距离dj(i),即:

(5)对每个i,求出所有的j对应的lndj(i),求出算术平均值再除以Δt,即:

式中:q为非零dj(i)的数目。
做出回归直线,该回归直线的斜率为最大Lyapunov指数值。
采用小数据量法求失速状态下叶轮处压力时间数据序列的最大Lyapunov指数,图8所示为Lyapunov指数计算图。

图8 压力时间数据序列的Lyapunov计算图Fig.8 Lyapunov calculation chart of pressure time series
根据小数据量法的计算,上述叶轮处压力时间数据序列的Lyapunov 值为0.039 8,其值大于0,这同样表明了叶轮处压力时间数据序列的混沌性。
3.3 G-P算法的关联维数混沌评判
离心通风机失速下叶轮处压力时间序列为:

式中:x(i)为i时刻的压力数据;N为数据个数。
重构相空间中数据量可以表示为:

式中:M=N-(m- 1)τ;m为嵌入维数;τ为延迟时间;M为相点数量。
奇异吸引子上X(i)和X(j)两点之间的距离为:

给定m和τ,奇异吸引子的关联维数可以表示为:

式中:C2(r,m)为r(i,j)小于r的概率,即积累距离分布函数。

式中:θ()为Heaviside函数。

实际计算时,画出lnr- lnC2(r,m)的曲线图。如果随着嵌入维数的增加,lnr- lnC2(r,m)的曲线逐渐密集,如lnr- lnC2(r,m)的曲线密集到斜率几乎不变,就证明混沌存在。
对上述叶轮处压力时间数据序列采用G-P 算法计算饱和关联维数。图9 所示为叶轮处压力时间数据序列的lnr- lnC2(r,m)关系曲线。由图可知,lnr- lnC2(r,m)曲线随嵌入维数增大而逐渐趋于稳定平行,即关联维数达到饱和,这同样表明叶轮处压力时间数据序列数据呈现混沌特性。

图9 关联维数分析Fig.9 Correlation dimension analysis
上面从相图法、最大Lyapunov 指数计算和关联维数分析对失速后的压力时间数据进行分析,失速后的压力时间序列呈现混沌特性。
4 结束语
(1)失速工况下的压力高于正常工况下的压力,且失速下的蜗壳出口处形成局部高压区。
(2)对失速状态下的压力序列的相图分析得出,二维相图在有限的区域内具有一定的聚集性,三维相图同样具有一定的规律性,进而判断其混沌性。
(3)对失速状态下的压力序列的最大Lyapunov 指数计算,其值大于0,另外,关联维数分析表明其呈现饱和性,这在多维度方面判断了失速下的混沌特性,为离心通风机失速状态下的特性辨识提供了一定的参考。
