干涉仪测向影响因素分析

刘 飞

(中国电子科技集团公司第29 研究所,四川 成都 610036)

0 引言

随着电子对抗技术的发展,对无线电目标进行精准的测向成了关键手段,其中被动测向技术中的干涉仪测向因其能实现较高的测向精度而被研究人员高度重视。由采取其测量多个天线之间信号到达天线的相位差来计算信号入射方向。这个过程影响因素多、过程复杂,本文就从理论入手分析影响干涉仪测向的几个因素。

1 基本原理

根据肖秀丽[1]干涉仪测向的基本原理如图1 所示。

图1 干涉仪测向基本原理

雷达信号的到达角θ,到达两个天线之间的相位差:

上式中,λ为电磁信号波长,L为两天线之间的距离,Φ为信号到达两天线的相位差,θ为信号的入射角度。由式(1)可以得出,可以把入射角度表达成φ的反正弦函数:

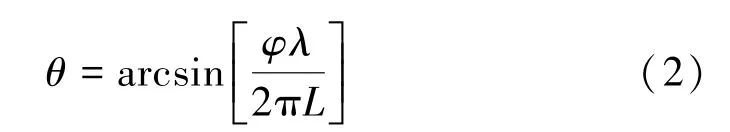
对式(1)进行全微分可以得到:

从式(3)可以测向误差来至波长误差(测频),基线误差。如果波长误差和基线误差忽略,那么公式(3)可以简单记如下:

从式(4)可以得到如下结论:

(1)测量角度误差和相位误差成正比,而其中的相位误差,由直接测量信号的相位差得到,要测量信号的相位差不可避免地受到通道一致性和信号强度(信噪比)的影响。

(2)测量角度误差和基线长度L成反比,基线越长测量角度的误差越小,但由于实工程上受到基线布置条件的限制,基线不可无限增加,其次由于受到信号周期性影响,测量相位存在2Kπ 的模糊,为了解算模糊,基线越长,需要的基线数量越多,受到限制的条件越多,因此实际基线长度有限。各个文献中讨论关于基线的布置非常多,大多是采用长短基线结合的解模糊方式来完成角度解模糊[2-3]。本文不参与讨论关于基线选取的问题。

(3)测量角度误差和cosθ值成反比,cosθ值越大测量精度越高,当cosθ=1,(θ=0°)时测量精度最高,当cosθ=0(θ=90°)时,误差无穷大,无法测向。实际上信号不像理想情况一样和天线在水平方向上入射,实际入射是在俯仰方向还有一个夹角α需要考虑。

本文从上文相位误差和入射角度来简要分析干涉仪测向和各个因素对测量的影响。

2 相位误差的影响

干涉仪测向中相位差Φ是以2π 为周期循环的,从式(4)可以得出,要测向角度误差小,就必须要有足够的基线长度L,基线L越长得到的测角精度越高,但基线变长,则会导致相位测量模糊,为了不产生相位模糊,基线要足够短。这两者之间是矛盾的,实际工程中研究人员采用多基线组阵的形式来化解这个矛盾。以数字信道化分机技术鉴相为背景,在多基线中必然出现多个天线,多个变频通道,多个AD 变换器。

从图2 看出组成各个通道的包括天线、前端放大、变频、AD 采样,还有连接电缆。从这个主场框图可以看出,各个支路受到存在通道一致性影响,要做到一致是很困难的;每个支路存在天线、放大器、下变频、AD采样处理的情况。这是一个典型的信号处理通道,放大器和变频器都存在自身的热噪声,和其他信号处理一样,存在一个信号强度(信噪比)的问题。

图2 干涉仪通道组成

2.1 通道不一致的影响

在实际工程中要做到各个通道相位完全一致,概率是极小的。电缆加工最多做大5°的相位一致性,放大器,变频器等15°～20°的相位不一致,这个不一致性和频率、温度湿度、连接器特性相关。整个通道上(到达AD 采样之前)相位偏差大约会到10°～30°典型通道上的相位偏差如图3 所示。

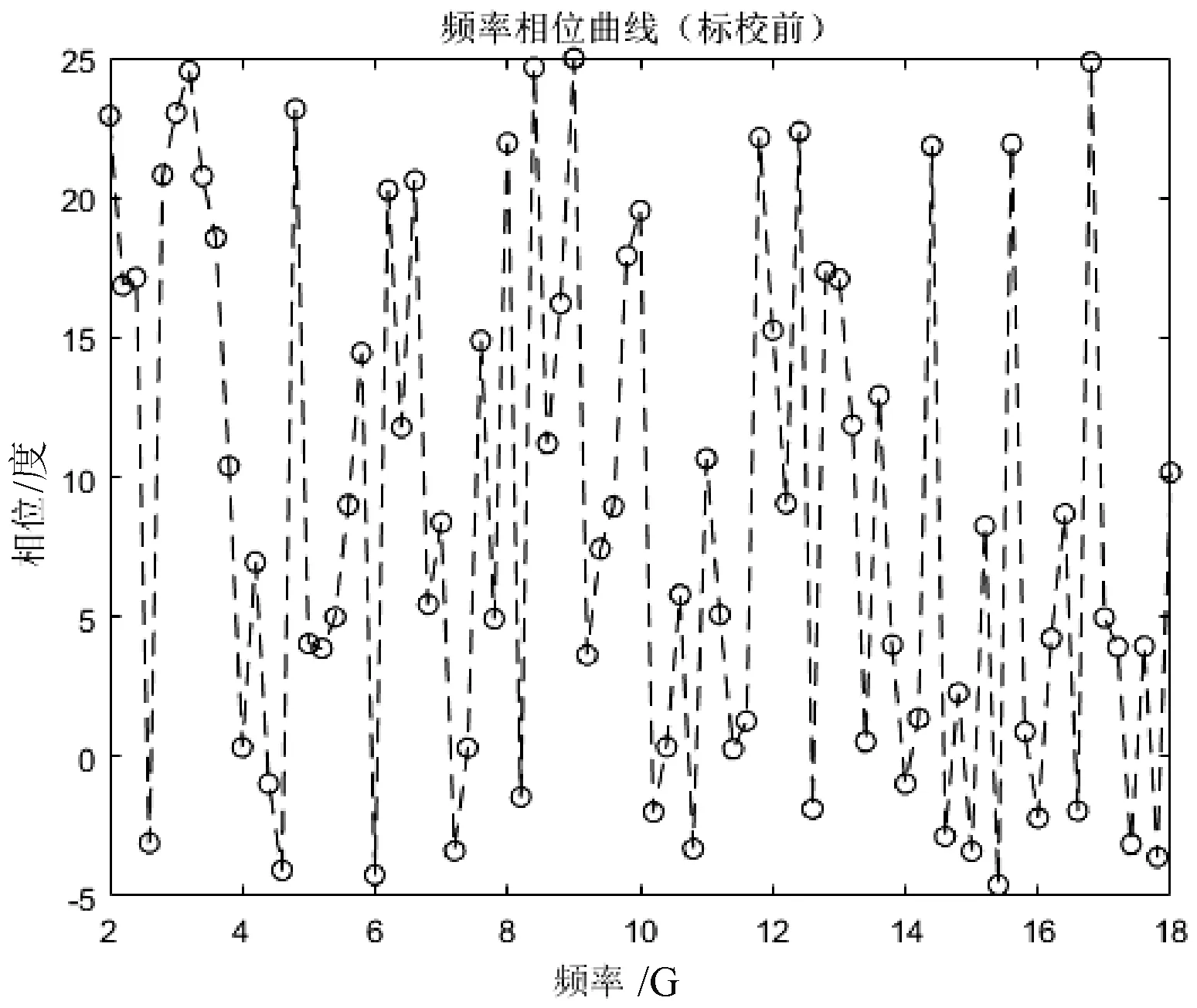
图3 典型通道上的相位偏差

本文假设采用10 倍波长的基线测量角度,那么30°左右的相位偏差会带来多大的测向误差,此问题值得研究。

根据公式(4),将基线10λ、入射角度45°、相位偏差30°各条件带入,可以得到θ 偏差在4.2°左右。此条件在对测向要求很高的应用场景是不能满足要求的。

但此偏差通常在不同通道上表现相对一致,和频率对应关系比较稳定,例如A 通道固定向某个方向偏移固定值,可通过校准源校准其偏差。从而在计算时将校准信息纳入其中减少相位固定误差。仅留下随机偏差。从图4 可以看出,校准后的相位随机误差,校准的效果十分可观。

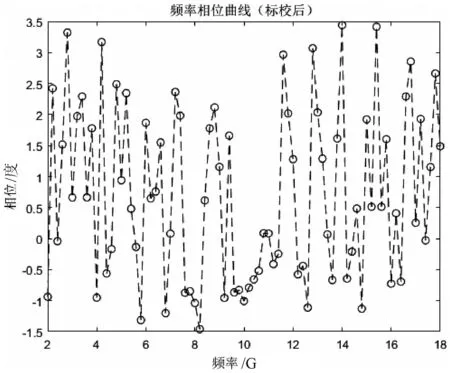
图4 校准后的通道相位情况

从校准后的相位误差看,大致控制在4°左右,通过公式(4)的计算,这一偏差带来的测向误差不超过0.5°,因此能够满足一些测向精度要求较高的场景。

2.2 信号强度(信噪比)的影响

从图2 示意图看出,在天线接收后,信号经过放大、变频处理才会进入数字化通道,在AD 之前,都为典型的模拟通道,与其他的信号处理一样面临着信噪比的问题。

在整个计算过程中,FFT(Fast Fourier Transform)的积累长度和基线长度都是关键因素,选取64 点FFT(Fast Fourier Transform)积累,10 倍波长的基线长度。用高斯白噪声加正弦信号进行仿真计算得到如下曲线图(见图5)。

图5 信噪比和测向精度之间关联

从图5 中看出,当信噪比到14 dB 以上时,测向精度达到比较理想的状态。这个精度和FFT(Fast Fourier Transform)积累长度、基线选取高度关联。其中天线阵的布置和基线长度选取在业内讨论较多。

3 入射角度的影响

在式(1)中,仅仅考虑了目标和测试天线在同一水平面的情况,实际工程应用中,天线位置和目标位置时刻都在一个水平面上的概率极小,这样实际工程中研究人员不单需要时刻测量水平角度,还需同时测量俯仰角。假设俯仰度为α,水平角度为θ,水平基线L1,俯仰基线L2,可以得到式(5)、(6):

上式中ΦA为水平向(入射波投影和天线法线方向夹角)相位差,ΦB为俯仰向(入射波和水平面夹角)相位差。可见在实际工程上水平方向测向会包含一个α 的倾角因子。此倾角可能来自目标不在水平面上,也可能因为天线安装而不在水平面上(和水平面有夹角)。

从公式看这个倾角最佳是0°。意味着:(1)天线法线最佳是在水平方向;(2)目标最佳是在天线一个水平面上。条件(1)可以通过天线的安装较容易实现,条件(2)要求能够在大部分工程中忽略,例如天线安装在飞机上,目标和飞机在近似高度2 km 左右,目标距离飞机30 km 甚至更远,其这个夹角很小接近0°可忽略,研究人员认为无较大影响。但在飞机做机动的时候,其角度就不能被忽略,这是飞机大机动条件下,测向跳跃的原因之一。

4 结语

干涉仪测向的影响因素很多,天线布置、基线长度、信噪比、入射角度、通道一致性及其选取的信号积累方式都高度关联。实际工程上由于多种因素的交叉影响,测向精度大多保持在0.5°～1.5°。这篇文章从通道一致性和信噪比、入射角等角度讨论,希望能够给工程技术人员提供一个新的思路。