初中数学“命题、定理、证明”教学研究

李庾南 刘东升

摘要：七年级平面几何入门阶段，关于“命题、定理、证明”的教学研究往往是各级教研活动的一个薄弱点。如何将这部分内容中比较抽象的数学概念形象生动地呈现出来？怎样把这些零散的概念或知识点串联起来？可以从理解课标、理解教材出发，梳理出思维导图，精选典型实例改编成“问题串”，驱动结构化认知的生成。

关键词：“命题、定理、证明”;教学研究;结构化认知

本文系江苏省教育科学“十四五”规划课题“高质量发展视域下‘三学’立人的实践研究”（编号：TSXM/2021/06）的阶段性研究成果。课题主持人：李庾南、祁国斌。七年级平面几何入门阶段，关于“命题、定理、证明”的教学研究往往是各级教研活动的一个薄弱点。从一些随堂课的观课情况来看，有些教师在教学中确实存在“一个定义、三项注意、大量练习”（章建跃语）的问题。如何将这部分内容中比较抽象的数学概念形象生动地呈现出来？怎样把零散的概念、知识点串联起来？最近，我们在集体备课时，对这些问题做了较为深入的教学研讨。

一、知识梳理与解读

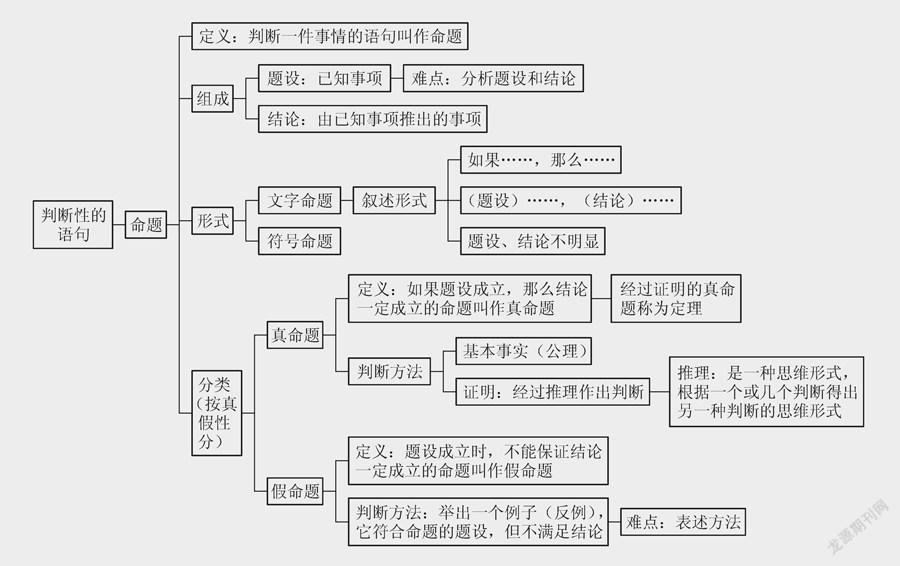
我们首先对人教版初中数学七年级下册 “5.3.2命题、定理、证明”的内容做了知识梳理与解读，预设出所要形成的知识网络（如下页图1所示）。

根据《义务教育数学课程标准（2022年版）》的要求，七年级新授阶段，只要求学生“通过具体实例，了解定义、命题、定理、推论的意义。结合具体实例，会区分命题的条件和结论”。考虑到几何内容分布在不同分册教材中，对于命题的相关知识，人教版教材也是分散安排的，教学时要注意把握七年级的教学要求，特别是“结合具体实例”帮助学生了解相关概念。

二、教学设计

（一）生成“命题”概念

问题1研究下列语句的特点，侧重分析它们是否是对某个数学概念或性质的判断。

（1）如果两个角互补，那么它们的和为180°;

（2）作∠AOB的平分线OC;

（3）a的相反数为-a吗？

（4）∠AOB=90°，AO⊥BO;

（5）直角都相等;

（6）相等的角都是直角。

在学生分析上述语句的特点之后，抽象概括出命题的概念及构成（命题由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项）。需要讲解清楚的是，命题常写成“如果……那么……”的形式，“如果”后接的是题设，“那么”后接的是结论。在此基础上，继续安排一组习题，让学生判断这些语句是不是命题，如果是命题，则判断命题是否正确。即让学生“回到命题的定义”去解题，将命题的概念具体化，通过恰当、必要的追问，让学生知道命题中需要有“一件事情”和“判断”等关键信息。

（二）辨析命题的“题设”和“结论”

问题2分析下列命题的题设和结论。

（1）如果两个角互为补角，那么这两个角的和等于180°;

（2）如果x=0，那么xy=0;

（3）大于90°而小于180°的角是钝角;

（4）直角都相等;

（5）同角的余角相等;

（6）内错角相等。

前两个小问，学生容易分析出“如果”后面是题设，“那么”后面是结论;后四个小问，可以引导学生先将它们改写成“如果……那么……”的形式，再来辨析它们的题设和结论。讲评这个问题时，教师还要注意以下两个方面：一是让学生知道命题既有文字命题的形式，也可以用符号语言来表示，如第二小问;二是帮助学生根据已有的经验，学会判断命题的正确性。进一步地，按命题的真假性，可以将其分为真命题和假命题两类。

（三）了解“推理”“证明”和“定理”

问题3判断命题“垂直于同一直线的两直线平行”的真假，并说明理由。

在训练命题真假性判定的基础上，让学生了解推理和证明的意义，体会推理、证明的基本步骤，并初步学习数学文字语言与图形符号语言的互化，为以后证明文字命题奠基。在推理过程中运用到的依据，一般有定义、公理、基本事实、定理、推论等。这里，可让学生了解定理的概念，即经过推理证实其为真并且可以它为依据推证其他命题的真命题叫作定理，定理是重要的真命题。顺便可让学生回顾已经学过的一些定理、公理（或基本事实）。

问题4判断下列命题的真假，如果是真命题，说明理由;如果是假命題，举反例说明。

（1）如果两个角互余，那么这两个角都是不大于45°的角;

（2）如果a+b>0，那么a>0，b>0。

教学时要让学生知道，真命题无一例外总是正确的，而假命题则不能保证总是正确的，只要能找到一个反例，就可以说明某个命题是假命题，从而帮助学生正确理解命题的真假性。

（四）完善结构化板书

问题5本课我们学到了哪些数学概念，举例说说你对它们的理解。

问题6证明“两直线平行，同旁内角的平分线互相垂直”这道文字命题时，你觉得要分哪几步？

问题5是开放性的，学生可结合本课所学，先小组内交流，再全班汇报，教师进行必要的追问，并完善、形成本课的结构化板书（类似图1）。对于问题6中文字命题的证明，要让学生知道应先分析命题的题设和结论，然后将文字命题的题设、结论分别转化为图形语言和符号的形式，再进一步去分析证明思路，书写推理过程。具体的解答过程，则可以作为课后作业安排学生完成。

三、教学立意的进一步阐释

在研究某个课时的教学时，首先要查阅国家颁布的学科课程标准。课程标准一般从整个学段（如初中为7—9年级）提出某个知识点的教学要求，我们可以在此基础上厘清本课时教学的具体要求。“命题、定理、证明”在初中学段只要求“结合具体实例了解”，那么本课时就要注意放低起点，精心挑选恰当的实例来帮助学生理解这三个概念。比如，在生成“命题”概念时，问题1中（1）是对“和”作出判断，（2）是祈使句但不是判断句，（3）是疑问句但未作出判断，（6）是判断但判断不正确。由此，学生可以明确，命题中需要有“一件事情”和“判断”等关键信息，从而将抽象的“命题”概念具体化。

特别要指出的是，有些教辅资料随意编写一些生活中的语句，如“今天的天气真好”“这本书你看完了吗”等，让学生辨析它们是不是命题。我们认为，这些没有数学味的语句属于“无趣题”，对学生理解数学命题的概念意义不大，不宜出现在数学命题的教与学中。

人教版初中数学教材在“命题、定理、证明”这一课时的内容安排上，以大段文字的讲解为主，比较抽象，我们在研读教材的基础上，先将本课中一些概念之间的关系梳理成思维导图，再选编几组“问题串”，分别在这些“问题串”的驱动之下依次引出命题、定理和证明的概念，并渐次生成结构化板书，使得教学环节分明、层层递进、渐次生长。这也是教师需要加强修炼的基于教材的加工转化能力。