奥苏伯尔认知同化理论对中学数学教学的启示

施佳莹 喻平

摘要：从有意义学习的本质特征、认知同化理论的基本要义、有意义学习的教学原则、实现迁移的条件等四个方面，解读奥苏伯尔的认知同化理论，梳理出对当下中学数学教学的启示。一是建构有意义学习的教学环境，包括设置恰当情境、连通知识序列。二是制订完善学生认知结构的教学策略，包括活用先行组织、突出渐进分化、强调综合贯通、提倡迁移训练。

关键词：认知同化理论;有意义学习;中学数学;认知结构

本文系喻平教授团队的“数学学习心理学研究及其教学启示”（中学）系列文章之十二。从本文开始，系列文章的主题从数学学习心理学的基本概念（方面）变为经典理论（思想）。学习者学习新知识，需要将认知结构中的旧知识与其相互作用，这个过程称为同化;当新知识被纳入认知结构，又会对旧的认知结构进行改组，形成新的认知结构，这个过程称为顺应。这是源自皮亚杰的结构主义、发展于奥苏伯尔的有意义学习理论的知识建构观。本文尝试解读奥苏伯尔的认知同化理论，并谈谈这一理论对当下中学数学教学的几点启示。

一、奥苏伯尔认知同化理论的主要观点

美国著名教育心理学家奥苏伯尔系统研究了课堂教学中有意义学习的类型、结果及条件，深入探究了影响学习的内因和外因，提出了以言语符号为媒介、以学习者原有认知结构为核心、以接受学习为主要學习方法的有意义学习理论。有意义学习的过程是认知同化过程，因此该学习理论又可称为认知同化理论。

（一）有意义学习的本质特征

有意义学习的过程，本质上即符号所代表的新知识以非任意的方式，在实质上同学习者认知结构中的适当观念相互作用、产生联系的过程。D.P.奥苏伯尔等.教育心理学——认知观点[M].佘星南，宋钧，译.北京：人民教育出版社，1994：45。奥苏伯尔认为，新知识与认知结构的原有成分之间的联结是有意义学习与机械学习的主要差异：机械学习中，联结是简单的、任意的、非实质性的;而有意义学习中，联结是“非任意的”和“实质性的”。

“非任意的”亦称“非人为的”，指新知识与认知结构中的有关观念之间存在着某种合理的或逻辑基础上的联系。陈琦，刘儒德.当代教育心理学（第三版）[M].北京：北京师范大学出版社，2019：116。奥苏伯尔认为，具有非任意性的学习材料是学习者开展有意义学习的先决条件。若知识点之间没有逻辑关系，即便学习者采用特殊方法（如谐音联想法），人为地为其创造“意义”，这类学习也是机械的。若新知识是在旧知识的基础上增添、限制、变化某些条件或结论演变而来的，或新知识与较为普遍的观念有一般的吻合关系，学习者就有足够的依据将两者以非任意的形式联系起来。

“实质性”亦称“非字面性”，指能用同义词或其他等值符号替代而不改变意义或内容。教育大辞典编篡委员会.教育大辞典（第5卷）：教育心理学[Z].上海：上海教育出版社，1990：267。奥苏伯尔指出，学习者的学习结果要符合实质性标准，如果使用同义词或其他等值符号替代概念或者命题中的部分词汇，学习者要能判断其意义或内容是否发生变化。例如，“三角形的内角和为180°”与“三角形的内角和为平角”是等价的。如果学习者的学习只停留于字面意义，没有深入思考、挖掘知识本质，则认知结构不稳固，后续学习过程中也很容易受到以前学过的类似材料的干扰。

（二）认知同化理论的基本要义

其一，认知结构在学习中起着决定性作用。在奥苏伯尔看来，认知结构就是个体头脑中的知识结构。广义地说，它是学习者已有观念的全部内容及其组织;狭义地说，它是学习者在某一学科的特殊知识领域内的观念的全部内容及其组织。皮连生.智育心理学[M].北京：人民教育出版社，1996：220。形成优良的认知结构是学习达成的关键。奥苏伯尔认为，良好的认知结构取决于三个因素：（1）可利用性。当学习者面对新的学习任务时，他的认知结构中具备可以用来同化新知识的较一般的、概括的、包摄程度高的观念。（2）可辨别性。当原有观念同化新知识时，可以清晰地辨别新旧观念的异同点。（3）稳定性。原有的、起固定作用的观念稳定地贮存于认知结构中。

其二，知识同化存在三种样态。奥苏伯尔认为，同化是新旧观念相互作用、两者意义双向变化的过程，新知识获得心理意义，原有认知结构发生改组。新旧知识之间的同化有三种方式：（1）下位学习。在原有观念基础上，学习包摄性更低的观念。下位学习又分为派生归属学习（新观念可视为原来认知结构中上位概念的具体例子）和相关归属学习（新观念是对原来上位概念的精细化）。（2）上位学习。在原有观念基础上，学习包摄性更高的观念，即原有观念是新观念的具体例子。（3）并列组合学习。新旧知识有联系，但它们之间没有包含关系。

在此基础上，根据数学学习的特性，可以提出同位学习的概念。喻平.数学教学心理学（第2版）[M].北京：北京师范大学出版社，2018：262。所谓同位学习，是指对等价可同构命题的学习。在数学学习中，除了上位与下位的关系外，许多概念、命题之间存在等价关系，概念域、命题域的形成就是一个同位学习的过程。

（三）有意义学习的教学原则

奥苏伯尔提出了有意义学习的四条教学原则：渐进分化原则、综合贯通原则、序列组织原则和巩固性原则。

渐进分化指首先呈现最一般和包容范围最广的观念，然后由这些观念依照细节、特例和具体项目逐步展开。在下位学习中，归属过程一次或多次出现，便会导致起归属作用的概念或命题的渐进分化。奥苏伯尔认为，按包容性、抽象水平逐渐下降的纵向方式建立认知结构的层级组织，有利于新知识的同化和保持。

综合贯通指加强知识横向与纵向的联系。在上位学习或并列组合学习中，发现认知结构中原有观念之间的联系，对其进行重新组合的过程，就是综合贯通。奥苏伯尔指出，综合贯通能促进原有认知结构的横向分化，是渐进分化的一种形式。当教学材料没有实质上的序列相依关系时，综合贯通原则也是适用的，可以横向加强学科知识点、章节内容之间的联系。

序列组织亦称先行组织，指学习新知识之前，给学习者提供一个引导性材料，它比学习任务本身有更高的抽象、概括和综合水平，并能使学习者清晰地辨认认知结构中原有的观念和新学习任务的关联。序列组织强调学科知识内部的逻辑结构，新学的知识被同化后可以作为后续学习的先行组织者，促进后续知识的学习与同化。为了防止认知框架杂乱无序，学习任务的排列需要以学习者认知功能的发展水平、固着观念的可利用性和教材的序列组织为依据。

巩固性强调在学习新内容之前，要确保学生对已授知识的掌握程度较高。奥苏伯尔认为，清晰稳固的认知结构能为新知识的学习提供坚实的固着点，是有意义学习的先决条件。学习者可以通过反复接触学习材料，经历证明、分析、比较和反馈的过程，来明确新旧知识之间的联系，构成组织完善的认知结构。

前沿论坛（四）实现迁移的条件

迁移指先前学习的经验对当前学习的影响。与形式训练说、相同要素说、概括说等传统的迁移理论不同，奥苏伯尔认为，认知结构在学习迁移中起着决定作用。首先，先前学习的经验是经过若干知识的学习逐步积累而成的。迁移不能理解为某个知识点对当前学习的影响，而应是一组知识点对当前学习的影响。其次，先前经验的特征是指认知结构的组织特征，如清晰性、稳定性等。学习课题A得到的最新信息并不是直接同课题B的刺激反应成分发生相互作用，而只是由于它影響原有认知结构的有关特征，从而间接影响新的学习。再次，迁移的效果主要不是指提高将一般原理运用于特殊事例的能力（下位学习的能力），而是指提高上位学习和并列学习的能力。因此，无论是知识学习还是问题解决，只要认知结构影响新的认知功能，都存在着迁移。

二、对中学数学教学的启示

通过对认知同化理论的简单梳理，可以得到几个关键词：有意义学习、同化、认知结构。这几个词似乎有浓郁的传统观念色彩，与当下的教育理念有相悖之嫌。其实，每一种教学理论的创立及其具有的长久生命力，都足以说明它们存在的合理性。有意义学习与接受学习并蒂，这是事实，但是人类的学习不可能离开接受学习，而且接受学习还是学校教育的一种主要形式。况且，奥苏伯尔提出的有意义接受学习有别于传统意义上的接受学习，因为这种学习强调了同化与顺应的学习机制。同化事实上与知识建构的观念同出一辙，同化与顺应本质上就是个人对知识的建构过程，激进建构主义的观点与其一脉相承。认知结构的概念，无论是对建构主义还是对情境认知理论，都是认可的学习元素。因此，充分挖掘认知同化理论，对核心素养背景下的中学数学教学有直接的指导意义。

（一）建构有意义学习的教学环境

1.设置恰当情境，激发学习心向

“积极的学习心向”和“有逻辑意义的教材”是有意义学习的两个先决条件。

要激发学生积极的学习心向，教学情境的设计十分重要。奥苏伯尔认为，动机与学习是双向影响的，即便学生缺乏动机，若其满意初始学习的过程，也会产生极高的学习动机。因此，在课堂导入环节，教师可以暂时不理睬学生的动机，而关注学生的认知，尽可能有效地将他们带入教学情境：根据教学内容创设有效的问题情境，提供能引发学生认知冲突、质疑思考的信息，激发其好奇心和求知欲。

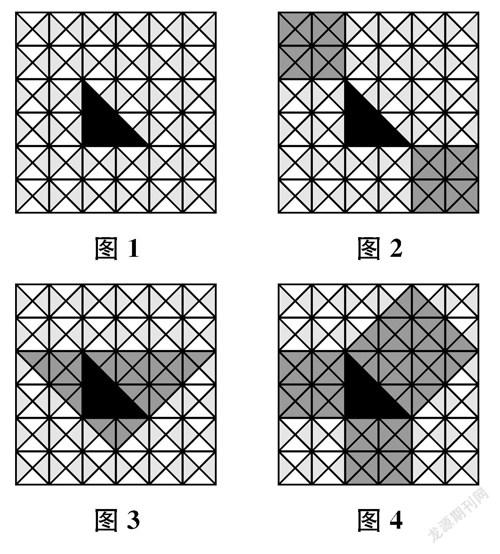
例如，《勾股定理》一课的导入环节，教师创设了如下情境：2500年前，毕达哥拉斯在朋友家做客时，发现朋友家用砖铺成的地面中反映出了直角三角形（如图1）三边的某种数量关系，便很快用画图形的方法表示出这种数量关系。接下来，教师把这个问题抛给学生，让他们尝试用数学的眼光观察图形，在准备好的纸上画出与该等腰直角三角形三边有关的几何图形。

勾股定理是平面几何中最重要的定理之一，融合了数形结合的思想方法。课例中，教师首先引用数学史，试图还原并让学生体验毕达哥拉斯发现勾股定理的过程。该情境的创设能有效激发学生的好奇心，让学生跃跃欲试，挑战自己能否得出与大数学家一样的结论。通过操作，可能有的学生画出的图形与教师的要求毫无关系（如图2），有的学生画出的图形与勾股定理较为接近（如图3），有的学生画出的图形与毕达哥拉斯的画法完全一致（如图4）。围绕学生的画法学习该图形与勾股定理的关系，不仅能增强学生后续学习的动力、信心，还能加深学生对新知识的理解与感知。

2.连通知识序列，促进同化顺应

教材通常都是按照知识之间的逻辑关系编排的，教师的任务是引导学生把这种逻辑关系清晰地表达出来。其中一个好的做法就是单元设计，因为知识的逻辑关系不是体现在知识点上，而是体现在知识群中，单元设计可以很好地揭示这种逻辑关系。喻平.数学单元结构教学的四种模式[J].数学通报，2020（5）：18。

既然同化是先前知识对新学知识的作用，顺应是新学知识对原有认知结构的改造，那么厘清知识的生成顺序就显得非常重要，因为“最邻近”的知识最利于同化，有序的知识利于形成结构。

例如，“四边形”单元的教学设计：

第一步，教师给出一般四边形的概念，让学生举出现实生活中四边形的实例。

第二步，教师引入“平行”概念，让学生思考问题：（1）是否存在两组对边分别平行的四边形？（2）是否存在只有一组对边平行的四边形？学生通过画图证实这两类图形都存在。于是，教师引导学生给第一类图形命名为平行四边形，第二类图形命名为梯形。

第三步，教师引入“相等”概念，引导学生分两条线探究：（1）是否存在一组邻边相等的平行四边形？（2）是否存在两条不平行边相等的梯形？学生通过画图证实这两类图形都存在。于是，教师引导学生给这两类图形分别命名为菱形、等腰梯形。

第四步，教师引入“垂直”概念，进一步引导学生探究：（1）是否存在一组邻边相互垂直的平行四边形？（2）是否存在一组邻边相互垂直的梯形？学生通过画图证实存在这两类图形。于是，教师引导学生给它们分别命名为矩形、直角梯形。

第五步，教师进一步提出问题：（1）是否存在一组邻边垂直而且相等的平行四边形？（2）是否存在一组邻边垂直而且相等的梯形？学生通过画图证实也存在这两类图形。于是，教师引导学生给它们分别命名为正方形、正方梯形。

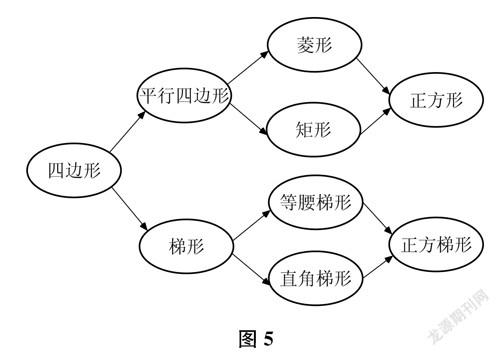
第六步，教师引导学生画出上述概念的体系图（如图5），并指出正方梯形的研究意义不大，可以不予考虑。

第七步，教师根据概念体系图指出本单元要学习的内容、要研究的问题：（1）如何从数学角度而不是仅用直观的方法，准确判定某些图形是平行四边形、菱形、矩形、正方形、梯形、等腰梯形、直角梯形？（2）这些特殊的图形具有什么性质？（3）这些图形的性质能够解决什么数学问题？能够解决哪些现实生活中的问题？

这样的设计就为本单元的知识教学做了铺垫，有助于学生在接下来的学习中实现知识的同化;同时又为形成知识结构进而转化为认知结构做了准备，使顺应得以完成。

（二）制订完善学生认知结构的教学策略

1.活用先行组织，激活认知结构

每堂课在讲授新知识之前，教师通常都会先引导学生复习旧知识。其实，复习旧知识就是一种先行组织。但是，如果只考虑旧知识，就窄化了先行组织者的概念。先行组织者是教学之前提供的一组辅助材料，可以把这种材料理解为几种情形：（1）它比新学习的知识概括性高，即提供一种上位概念，这是奥苏伯尔提出的先行组织者的原意;（2）它比新学习的知识概括性低，是新知识的特例，即提供一个下位概念;（3）它与新学习的知识成并列组合关系;（4）它与新学习的知识是等价关系;（5）它是包含新学习知识的一种情境——现实情境或科学情境。

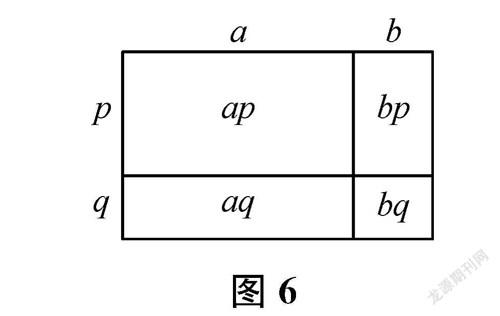
例如，《完全平方公式》一课，教师首先出示图6，让学生根据图中的边长关系，抽象出（a+b）（p+q）=ap+aq+bp+bq，分别用图形语言、文字语言、符号语言描述多项式乘法法则;然后将图形做特殊化处理，将p变为a，将q变为b，引导学生得出完全平方公式。这个先行组织者就是上述情形（1）。

又如，如果在讲授余弦函数y=cos x时，由正弦函数y=sin x引入，那么先行组织者就是上述情形（3）。

2.突出渐进分化，扩充认知结构

渐进分化主要是指梳理知识的纵向逻辑关系。按照奥苏伯尔的观点，概括性、抽象性高的知识应当放到前面，然后依次呈现概括性、抽象性递减的知识。其实，一般的数学教材中，许多知识体系都是遵循这个原则来编排的。例如，高中“函数”的知识体系，首先用映射定义函数概念，介绍函数的单调性、奇偶性等一般概念，然后研究具体的函数：幂函数、指数函数、对数函数、正弦函数、余弦函数、正切函数、余切函数等。这是典型的渐进分化。教学中，教师的一项重要工作，就是帮助学生梳理知识，并通过一定量的解题练习将这种外部的知识体系转化为学生头脑中的知识结构，使学生的认知结构得到不断的扩充。

另一方面，对问题进行适当的变式或推广，体现知识之间的纵向联系，可以使知识纵向发展，扩充学生的认知结构。

例如，一个与点的运动有关的线段长度（关系）问题及其变式：

原问题线段AB长为12 cm，P为线段AB上的一个动点。点P从点A出发，以2 cm/s的速度沿AB向点B运动，表示出t（s）后AP与PB的长度。

变式1在原问题的条件下，延长AB至点C，使BC=6 cm。点P到达点B后继续向点C运动，表示出t（s）后AP与PC的长度。

变式2在变式1的条件下，将线段BC绕点B逆时针旋转90°（如图7所示），表示出t（s）后AP与PC的长度。

变式3在变式2的条件下，添加另外两边，构成长方形ABCD（如图8所示）。点P到达点C后继续向点D运动，经过t（s）后，PC怎么表示？点P到达点D后继续向点A運动，经过t（s）后，AP怎么表示？t为何值时，AP=PD？

变式4在变式3的基础上，添加动点Q，点Q从点D出发，以1 cm/s的速度沿DA向点A运动。P、Q同时开始运动，t为何值时，下列等式成立？

（1）AQ=AP;

（2） AQ-AP=1/4CABCD。

变式5在变式4的情境中，点P、Q持续运动，直到点P到达点C，两点同时停止运动。t为何值时，等式AQ=1/2PC成立？

变式6在变式5的情境中，点P、Q向相反方向运动，点P能否追上点Q？如果能，求出t的值;如果不能，说明理由。

3.强调综合贯通，完善认知结构

通过综合贯通，可以建立更加稳固的外部知识结构，从而使学生的认知结构得到完善。对于知识之间的横向联系，很多情形在教材中不是以显性的形式表述的，需要教师去挖掘。例如，图5所示的“四边形”知识体系展示了知识之间的纵向联系，教师可以进一步挖掘知识之间的横向联系：平行四边形与梯形之间可以用中位线定理联系;菱形与矩形有共同的性质——中心对称图形;矩形与等腰梯形有共同性质——对角线相等;等等。

综合贯通不仅表现为搭建一个章节、一个单元知识之间纵向和横向的联系，还表现在建立不同章节或不同单元知识之间的联系。其中，通过数学思想方法打通知识之间的关系，是一条有效的途径。事实上，这也就是《普通高中数学课程标准（2017年版）》中十分强调的“通性”“通法”。

例如，可以用函数思想方法解决下列问题，从而串联有关知识。

问题1解方程3x+4x=5x。

显然方程有一个根x=2，但它是否还有其他根呢？将方程变形为35x+45x=1。引入函数f（x）=35x+45x，由于35x、45x是单调递减函数，则f（x）也是单调递减函数。易知x>2时，f（x）<1;x<2时，f（x）>1，所以方程仅有一个根x=2。

问题2已知e是自然对数的底，a、b为实数，且e<a<b，求证：ab>ba。

看到e，想到自然对数。要证明结论，就是要证明bln a>aln b，即要证明ln aa>ln bb。为此，构造函数f（x）=ln xx，只需证明f（x）在[e，+∞）内为减函数即可。求导，得f′（x）=1-ln xx2，因为x>e，所以lnx>1，故f′（x）<0，即f（x）在[e，+∞）内为减函数。

问题3求证：2C2n+2·3C3n+…+（n-1）nCnn=n（n-1）2n-2。

这是一个组合恒等式。联想到二项展开式，可以构造辅助函数f（x）=（1+x）n=C0n+C1nx+C2nx2+…+Cnnxn。求二阶导数，得f″（x）=（n-1）n（1+x）n-2=1·2C2n+2·3C3nx+…+（n-1）nCnnxn-2。在上式中，令x=1，即得所要证明的恒等式。

在此例中，问题1建立了函数与方程的联系，问题2建立了函数与不等式的联系，问题3建立了函数与组合知识的联系。

4.提倡迁移训练，稳固认知结构

奥苏伯尔认为，优良的认知结构是实现知识迁移的必要条件。反过来说，通过迁移训练，又能形成更加稳固、清晰的认知结构。用行为主义的观点看，这是一种强化。通过强化，才能建立刺激与反应之间稳固的联系。

关于迁移训练，张姝华等提出了一些策略，如模式识别的合理训练、源问题的恰当设计、靶问题的变式训练等。张姝华，喻平.问题解决中迁移的心理学研究及其对中学数学教学的启示[J].教育研究与评论（中学教育教学），2019（9）：2632。这里，我们特别强调通过迁移训练，达到巩固认知结构的目标。其中一条有效的途径就是解题后的反思，特别是反思能否采用多种路径解决问题。因为采用多种路径解决问题，涉及的知识和方法自然会更多，需要解题者在认知结构中激活、提取多种知识和方法。这就是一个巩固认知结构的过程。

例如，對于题目“已知|a|<1，|b|<1，求证：a+b1+ab<1”，罗增儒先生提出从知识链上展开、从转化链上联想、从数形结合上沟通等思路，从面积、方程、三角函数等方面思考，得到十几种解法，最后还对问题做了推广。罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，1997：192200。这里列举几种解法：

（1）a+b1+ab<1a+b1+ab2<1……（在知识链上展开，与不等式性质建立联系）;

（2）|x|<1x在-1和1之间存在λ>0，使得x=1-λ1+λ函数f（x）=1-x1+x的性质……（在转化链上联想，与函数建立联系）;

（3）在平面直角坐标系上取点A（1，a）、B（1，-b）、M（1-b，1-b）（a>0、b>0时的示意图如图9所示，其他情况可逐一讨论），有|a+b|2=S△AOB<S△AOB+S△AOM=a+b2+（1-b）（1-a）2=1+ab2（在数形结合上沟通，与解析几何建立联系）。