湖南紫鹊界梯田自流灌溉系统降水条件

危润初，张 豪，龙秋波，彭向训，周升健

1.长沙理工大学水利工程学院，长沙 410004 2.水沙科学与水灾害防治湖南省重点实验室，长沙 410004 3.洞庭湖水环境治理与生态修复湖南省重点实验室，长沙 410004 4.湖南省水利水电勘测设计研究总院，长沙 410008 5.湖南娄底市水文与水资源勘测中心，湖南 娄底 417000

0 引言

湖南紫鹊界梯田是“中国南方三大古梯田系统”之一，因其独特的自流灌溉系统而被列入首批世界灌溉工程遗产名录。作为历史悠久的农耕稻作系统，湖南紫鹊界梯田在无塘无坝、无人工水利设施条件下能够实现旱涝保收[1-2]，其内在水文机制对于构建现代人与自然的新型关系与乡村生态规划设计[3]具有重要的借鉴意义。

早在2005年，秦仁秋[4]就从地质、地貌、气象与人类活动等方面对紫鹊界梯田的饱水机制进行了简要阐述，而后相关研究逐渐深入。到目前，已有研究成果主要集中于以下几点：1)紫鹊界特殊的花岗岩地质条件使其风化层土壤具有渗透性适中、土壤含水量大、持水性好等特点[2,5-7]，这为梯田系统提供了很好的“天然条件水库”[8]；2)花岗岩基底为梯田系统提供了天然隔水层，使大气降水入渗至地下后在近地表的土—岩界面渗流，为梯田提供了自灌溉条件[1-2]；3)紫鹊界梯田分布具有明显的坡度规律，并有“顶盖帽”的特征，而植被对降雨入渗有着重要影响[9]，这自然形成了植被—土壤—地形—梯田的自适应系统[2,7,10-13]；4)千年来人类的深耕细作，整体上形成上下梯田“长藤结瓜”的自灌溉模式，同时又培育出特殊的稻田饱水层[2]。在上述研究的基础上，李桂元等[14-15]采用数字滤波法分析了梯田区的水源结构，并建立了古梯田原生态自流灌溉水供需平衡计算模型，精确给出了紫鹊界梯田原生态自流灌溉保证率，从定性、定量两方面深刻揭示了古梯田原生态自流灌溉机理。

作为一种特殊的人地复合型水文系统，降水在紫鹊界梯田运行过程中必然要起到重要作用。但是，除部分学者强调了区内降水总量外[2,10]，未见有对紫鹊界梯田自流灌溉系统降水条件的专门研究。本文从降水量、降水年内分配、干旱频率、降水条件与稻作制度匹配等角度出发，利用紫鹊界地区及外围共11个气象站1986—2015的年降水序列数据对紫鹊界梯田自流灌溉系统背后的降水条件开展研究，以期补充完善紫鹊界梯田水循环理论体系，为紫鹊界梯田开发和保护提供理论依据。

1 数据与方法

1.1 研究区概况

紫鹊界梯田位于湖南省中部偏西的新化县水车镇(图1)，是分布于海拔500～1 000 m的稻作梯田系统。整个梯田向东北方向呈扇形展开，范围约为93 km2[14]，共有梯田3 801.6 hm2，其中核心景区共有连片梯田1 334.0 hm2[8]。景区梯田主要分布在坡度为20°～40°的山腰，自下往上最大级数超过500。紫鹊界区域气候类型属亚热带大陆性季风湿润气候，四季分明，夏季湿热，冬季寒冷，多年平均降水量在1 600 mm以上，其中4—8月降水最为集中。

紫鹊界梯田基岩岩性主要以二长花岗岩为主，属白马寺复式岩体，于加里东期(志留纪)侵入。受白马寺岩体边界的控制，紫鹊界梯田所在的水车地区在地形上呈现为一开口朝南的簸箕形地形，核心景区最高峰海拔为1 585.2 m，地貌上属典型的中低山侵蚀地貌。

作为典型的人地复合型水文系统，人类活动在紫鹊界梯田的水文循环中起到了重要作用。一般来说，地形和地表土层的渗透性对降水入渗有重要影响[16]。通过坡改梯，改善了降水入渗的地形条件，延缓了汇流过程。同时，当地居民近千年的精耕细作孕育出特殊的耕作土层[4]，形成了相对隔水的保水薄层，而且还构建了“长藤结瓜”式的灌溉模式[2]，为水稻种植提供了优良的土壤与水源条件。

1.2 数据

本次研究收集了紫鹊界区域及周边地区共11个气象站1986—2015年的逐日降水数据，其中：半山、水车和双林等3个气象站位于紫鹊界；新化、溆浦、邵阳、洞口、隆回等5个气象站为国家气象基本站，数据下载自国家气象信息中心；其余站点为地方防汛气象监测站，数据源自湖南省水文与水资源勘测中心。

1.3 研究方法

1.3.1 集中度测定法

集中度测定法是一种用于评价降水或径流年内分配特性的计算方法[17-18]，目前该方法已经得到了广泛应用[19-21]。集中度(DC)是利用向量分析的原理定义气象或水文序列时间的分配特征。将一个时段(n)降水量或径流量的数值看作向量的长度，而对应的时段则当作向量的方向，把第一个时段方向看成0°，以后每个时段依次按(n/365×360°)等差递增，将第一个时段到最后一个时段的方位角θ分别设为0°，1×(n/365×360°)，2×(n/365×360°)，…，(n-1)×(n/365×360°)，把每个时段的降水量或径流量看作是有x、y两个方向分量，那么x、y两个方向的矢量合成及总向量[22]可表示为：

(1)

(2)

(3)

式中：t为年序数；i为时段序数；θ(t,i)为第t年第i个时段对应的方位角；Q(t,i)为第t年第i个时段的降水量或径流深，Qx(t)和Qy(t)分别为Q(t,i)第t年分解在x和y两个方向上的分矢量和；Qxy(t)为第t年的总矢量和。则第t年降水或径流的集中度(DC)和第t年年内最大降水或径流对应的集中期(PC)[22]分别为：

(4)

(5)

由式(4)(5)可以看出：DC能够反映研究时段降水或径流的集中程度，取值在0.0～1.0之间，若DC趋近于0.0，表示研究时段内降水分布均匀，DC值越接近于1.0，则表示降水或径流越集中于某一个时段内；PC表示的是合成向量的方位角，反映年内最大降水或径流的分布时段。

本次研究为了计算方便，对时段划分进行简化处理，将年总天数按360 d算，以旬为单位时段(10 d)，即将全年分成36旬，每旬对应方位角为10°，大月下旬大于10 d的和2月下旬小于10 d的均按10 d计。

1.3.2 标准化降水指数

标准化降水指数(ISP)是通过计算给定时间尺度内降水量的累积概率，使得降水量能够在多个时间尺度上进行计算比较[23]。在进行ISP计算时，首先假设某个时段的降水量分布是一种偏态分布，因此采用Γ分布概率来描述降水量的变化。在计算出某时段内降水量的Γ分布概率后，再进行正态标准化处理，最终用标准化降水累计频率分布来划分干旱等级[24]，其计算步骤如下：

1)假设某时段降水量为随机变量x，则其Γ分布的概率密度函数为

(6)

式中，β、γ分别为尺度和形状参数，β>0、γ>0。β和γ可用极大似然估计方法求得：

(7)

(8)

其中，

(9)

确定概率密度函数中的参数后，对于某时段的降水量x0，可求得随机变量x小于x0事件的概率F为

(10)

利用数值积分可以计算式(6)代入式(10)后的事件概率近似估计值。

2)降水量结果为0时的事件概率由下式估计：

(11)

式中：M为降水量为0的样本数；N为总样本数。

3)对Γ分布概率进行正态标准化处理，即将式(10)(11)求得的概率值代入标准化正态分布函数，即

(12)

对式(12)进行近似求解可得ISP的值：

(13)

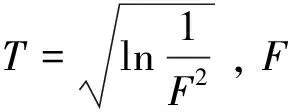
由上述ISP的计算步骤可知，标准化降水指数计算并未考虑不同季节降雨量的自然差别，这就使得计算的ISP序列会呈现出明显的雨→枯的年周期变化。这种计算结果虽然能够有效地反映出不同时间尺度条件下的水分变化[25]，但是很难反映雨季真实的丰枯情况。因此本次在计算前对各站30 a的月降水序列进行标准化处理，即将所有月降水样本xi除以该站样本xi所在月份的30 a降水的平均值，并以此标准的月降水序列开展ISP计算。

根据ISP值干旱等级划分标准[26]，对干旱进行等级划分(表1)，然后根据计算得到的各年不同时间尺度不同时间节点的干旱等级结果，对选定的时间尺度开展干旱频率分析(根据水稻需水情况，只统计中旱以上级别)，干旱频率Pj计算公式为

(14)

式中：J为该站选定时间尺度某时间节点发生中旱级别以上干旱的次数；K为样本总数(30)；j代表不同的时间节点。

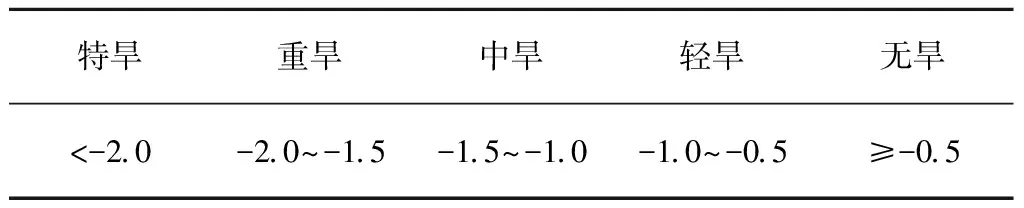
表1 ISP干旱等级划分

2 结果与分析

2.1 降水特征及干旱情势对比

2.1.1 年、季平均降水量对比

根据各站30 a降水监测资料，统计得到多年年平均及各季多年平均降水量，并绘制年均降水量空间分布图(图2)和各站季平均降水量对比图(图3)。从图2可以看出，紫鹊界区域是整个地区的降水量高值中心。本次研究所选取的紫鹊界外围地区8个站的多年平均降水量为1 461.3 mm，而紫鹊界地区的双林、水车、半山3个站的多年平均降水量平均值为1 638.7 mm，较外围8个站平均高出177.4 mm，其中双林站年平均降水量更是高达1 757.2 mm，比邻近的新化县城站高出308.4 mm，比隆回、邵阳等站更是高出400.0 mm以上。

图2 紫鹊界和外围地区年平均降水量空间分布图

由各站多年季均降水量对比图(图3)可以看出，研究区降水春夏多、秋冬少；紫鹊界地区3个站相对其他站点的多年平均降水高值优势主要由夏季降水贡献。外围8个气象站多年春季(3—5月)、秋季(9—11月)和冬季(12—2月)平均降水量分别为480.1、238.9、189.6 mm，紫鹊界3个站分别为501.7、266.5、195.4 mm，可见紫鹊界3个站在这三季并无明显降水优势；但是外围8个站的多年夏季(6—8月)平均降水量仅为552.7 mm，而紫鹊界3个站平均高达675.1 mm，较外围8个站平均高出122.4 mm。

2.1.2 集中度与集中期对比

运用集中度测定法对收集的11个气象站1986—2015年逐日降水数据进行处理，得到各站点DC与PC的多年平均值(表2)，并分别绘制DC与PC的空间分布图(图4)。由表2可知，研究区外围8个站的DC平均值为0.354，PC为15.16，紫鹊界地区3个站的DC平均值为0.373，PC为16.02。由此可知，紫鹊界地区3个站的DC值要大于外围8个站平均值，即全年降水更为集中，这与2.1.1节的研究结论相一致。

从空间变化趋势来看，本论文所采用的11个气象站所覆盖区域多年平均降水DC呈现出明显的自东南向西北逐渐增加趋势(图4)，紫鹊界地区处于高值区。而在PC方面，紫鹊界地区降水多年平均的高峰时段为6月中旬，而外围地区多为6月上旬，甚至是5月下旬。

2.1.3 基于ISP方法的3个月时间尺度的干旱频率对比

水稻灌溉保证率与农业干旱密切相关，而2个月时间尺度或3个月时间尺度的ISP可以很好地反映农业干旱情况[23]，同时5—8月的降雨情势对紫鹊界水稻生长影响最大。本研究基于11个气象站30 a的标准化月降水序列，计算得到各站1986—2015年5—8月3个月时间尺度的ISP值，在此基础上统计得到5—8月3个月时间尺度的干旱频率，并绘制干旱频率空间分布图(图5)。

从图5可以看出，紫鹊界及周边地区的干旱频率存在明显的空间变化，同时不同月份干旱频率也有较大差异。5月，整个区域干旱发生频率为5—8月期间的最低值，平均仅为11.5%，其中紫鹊界地区的3个站平均仅为11.1%，略低于外围8个站的11.7%；6月，虽然紫鹊界地区3个站平均干旱频率上升至13.3%，但远小于外围8个站的16.7%；7月，紫鹊界3个站与外围8个站的干旱频率对比关系翻转，前者平均值升至21.1%，后者则仅略升至19.6%；8月的全区域干旱频率相对7月有所下降，紫鹊界3个站平均值下降至18.9%，外围8个站则降至16.3%。

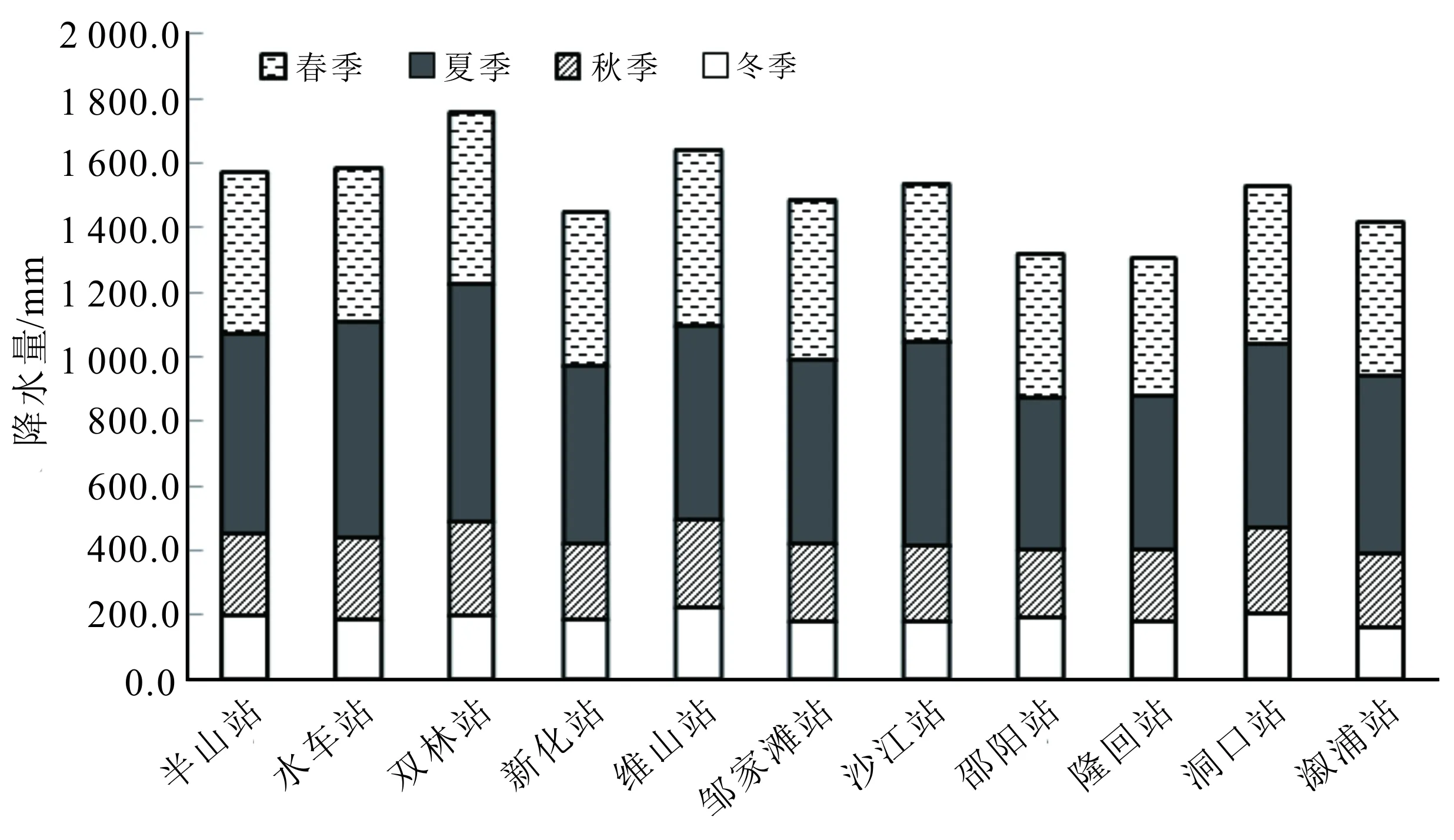
图3 紫鹊界和外围地区11个气象站多年季平均降水量对比

表2 紫鹊界及外围地区多年降水DC与PC计算结果

图4 紫鹊界及外围地区降水DC与PC等值线

从上述分析可知，紫鹊界地区3个月时间尺度在5—8月期间干旱频率有“先小后大”的特征，5月和6月的干旱频率明显要小于外围8个站平均值，7月和8月要大于外围8个站平均值。

2.2 紫鹊界地区降水优势控制因素

研究区位于长江中游流域，属亚热带季风气候，夏热冬冷，春夏季降水较多，秋冬季降水较少，季节变化显著[27]。按照季风的特点，可划分为夏季风(5—10月)与冬季风(11月—翌年4月)[28]。

夏季风期间，水汽主要来自孟加拉湾、南海洋面与西太平洋海区[28-29]，影响东亚夏季水汽输送的最主要的3个因素是印度季风环流、东亚季风环流和中纬度西风带[30]。在长江中下游地区，通过3大动力因素带来的气块(为研究方便而假设的一团相对于周围空气在热力上完全隔离的空气)分别占 44.0%、37.6%、18.4%，其中，印度季风环流带来的西南水汽是长江中下游峰值降水期的主要水汽来源[30]。郭海宇等[31]曾统计得出，在夏季风期间，湖南省偏南风占到所有风向中的 59.0%，其中西南风30.1%、南风14.7%、东南风14.2%。而在冬季风期间，水汽主要来自西风带携带的水汽和局地水汽环流[32]，水汽输送主要依靠西风环流和南下的大陆性气团[28]，风向上也主要以西北风为主。

由图1可以看出，紫鹊界至洞口、隆回和邵阳的一带区域，明显呈现为以紫鹊界地区为核心，在西南和东南两个方向开口的“漏斗状”地形，这种特殊的地形条件为紫鹊界的夏季降雨提供了有利的“聚水”条件。夏季风期间，来自印度洋的西南季风和来自太平洋的东南季风易受“漏斗状”地形的控制，汇于紫鹊界梯田所在区域，给紫鹊界梯田带来丰沛降水；而在冬季风期间，紫鹊界并无明显优势，这也是紫鹊界地区夏季降雨较外围气象站明显偏高的主要原因。

2.3 紫鹊界地区降水与水稻需水匹配度

水稻生长期主要包括返青期、分蘖期、拔节期、抽穗期、乳熟期和黄熟期等6个阶段，不同阶段水稻需水量会有差异。紫鹊界地处雪峰山区，梯田也多分布在于海拔500～1 000 m的山坡上，其水稻生长周期与湖南一般丘陵或平原地区有较大不同，但目前尚未见有专门的统计结果。根据本次研究在紫鹊界梯田调查的结果可知，紫鹊界山下水稻生长周期为120.0 d左右，在4月初至中旬播种，5月初至中旬插秧，9月初至中旬收割。受山地气候影响，山上水稻生长周期一般超过130.0 d，山上播种与收割时间较山下要晚15.0 d左右。本次研究选择与紫鹊界梯田海拔与纬度相近的的云贵地区的研究成果开展对比分析，以进一步明确水稻各生长阶段的时长。2014年，符娜等[33]对我国西南地区的48个地区的水稻生长期及需水量进行了专门统计，其结果(表3)表明，云南、贵州、四川、重庆4省市单季稻生长期不同阶段平均天数非常接近，分别约为9.0、35.0、17.0、13.0、13.0、12.0 d，平均生长周期在89.0 d左右(不含育秧期)，与紫鹊界梯田基本一致。本次研究参考云贵地区水稻各生长周期特点来大致确定紫鹊界梯田单季稻生长期不同阶段的时段分布(图6)。

图5 紫鹊界和外围地区5—8月3个月时间尺度的干旱频率空间分布图

一般来说，在插秧返青后，拔节期和抽穗期对稻田缺水最为敏感[34]，而分蘖期需水量最大。因此，在紫鹊界地区，6月上旬—8月中旬是水稻灌溉的主要时期。由前文的研究可知，紫鹊界地区夏季(6—8月)降水量比外围8站要高出122.4 mm，同时其降水多年平均的高峰时段为6月中旬。可见，紫鹊界地区降水的年内分配特征与紫鹊界梯田的水稻生长期形成良好的匹配关系。

从干旱角度来看，紫鹊界梯田3个月时间尺度的5月和6月干旱频率要小于全区域平均值，而6月中下旬是水稻分蘖期，该时期需水量大，较低的干旱频率为水稻的生长提供了水源保障。我们也注意到，紫鹊界地区7月、8月的干旱频率要大于全区域平均值，这可能会对梯田区水稻生长产生一定影响，但是区内独特的地质与土壤条件有效地抵消了这种影响。根据李桂元等[15]在紫鹊界梯田开展的抽水试验和压水试验结果，紫鹊界梯田花岗岩风化层的渗透系数在0.08～0.11 m/d间，接近粉土到粉砂的水平，而给水度在0.10～0.15间，接近细砂和中砂水平。紫鹊界风化层这种中等渗透性、较高给水度的特征，使其兼具黏土和砂的优点，即既能保水、又能给水，从而拥有了良好的调蓄能力。5月，紫鹊界梯田区进入雨季，为育秧、泡田、翻耕提供了足够水分；6月中旬进入降雨的高峰期，丰沛降水不仅直接为水稻分蘖提供水分，同时也通过地表入渗至土壤并蓄存在花岗岩基岩面以上的风化带空隙中，并在后期缓慢排泄出地表；当7—8月遭遇干旱时，蓄存在风化带孔隙中的水分就成为紫鹊界梯田的主要灌溉水源。也要注意到，虽然花岗岩风化层渗透系数不大，但由于梯田区坡度较大，如果较长时间得不到降水补充，地下水仍然可能会失去对梯田系统的补给能力。由降水PC的计算结果可知，紫鹊界地区的多年平均降雨高峰期为6月中旬，相较于其他区域要晚10～20 d，这实际上提高了梯田区7月和8月的灌溉保障能力。

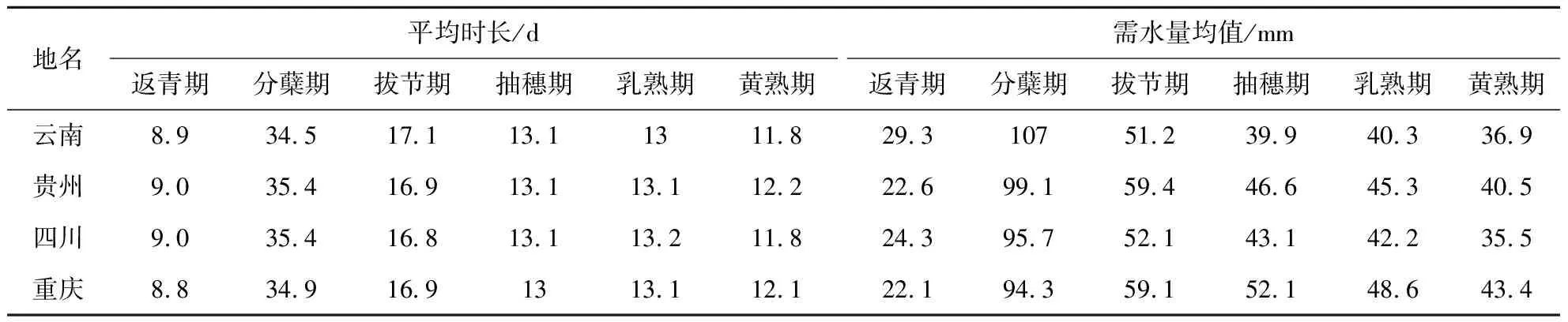
表3 云贵地区单季稻水稻生长期需水量统计[33]

图6 紫鹊界梯田单季稻生长期不同阶段时段分布

3 讨论

1)紫鹊界梯田自流灌溉系统是人类智慧与天然条件的完美结合，降水对自流灌溉系统的贡献也必然要通过其他条件来实现。花岗岩土壤的独特性质，提供了良好的入渗条件、蓄水条件和给水条件，花岗岩低裂隙基底的隔水作用为地下水自然补给梯田奠定了基础，而人工改造梯田又客观上延缓了地表降雨汇流过程、延长了降雨入渗时间，从而增加了降雨入渗量。因此，对紫鹊界梯田自流灌溉系统的认识，需要秉持系统的观点，将降雨、土壤、岩石、植被、地形、人工梯田以及稻作制度联系起来做整体思考，才能真正地理解紫鹊界梯田自流灌溉系统内在的水循环机制。

2)对于山区来说，降雨一般存在“迎风坡”和“背风坡”的差别，而观察紫鹊界的梯田分布就会发现，区内梯田分布有明显集中于南坡的规律。由于区内没有开展南坡和北坡降雨差异对比研究的气象资料条件，因此，紫鹊界梯田分布的南北坡空间差异规律是否与降雨有关，还需要在以后的研究中进一步深化。

4 结论

1)受独特的南向开口“漏斗状”地形条件的影响，紫鹊界地区拥有比外围地区更为丰沛的降水。区内3个站多年平均降水量达1 638.7 mm，比外围8个站平均高出177.4 mm。同时，受长江流域季风与地形条件的双重影响，紫鹊界的降水优势主要集中于夏季(6—8月)。夏季紫鹊界地区3站平均降水高达675.1 mm，比外围8个站平均高出122.4 mm，这也反映为紫鹊界地区降水的高集中度值。紫鹊界地区3个站旬降水序列的平均集中度为0.373，明显高于外围8个站的平均值0.354，紫鹊界地区3个站多年平均降雨高峰为6月中旬，晚于外围8个站的6月上旬或5月下旬。

2)紫鹊界及周边地区的干旱频率存在明显的时空分异。紫鹊界地区5—8月3个月时间尺度的干旱频率有“先小后大”的特征，3个月时间尺度的5月和6月干旱频率分别为11.1%和13.3%，明显小于外围8个站的平均值(11.7%、16.7%)，7月(21.1%)和8月(18.9%)则要大于外围8个站的平均值(19.6%、16.3%)。

3)紫鹊界地区一般在4月底育秧、5月底移栽，6月上旬—8月中旬是梯田灌溉的主要时期。6月，紫鹊界区域降水集中、降水量大、干旱频率小，为该时段内水稻生长提供了良好的降水条件，同时充沛降水通过表层入渗补给至具有中等渗透性、高给水度特性的花岗岩风化层，为7—8月水稻生长储备水源。紫鹊界地区降水年内分配、多年平均干旱频率分布特征等与紫鹊界梯田的水稻生长期形成良好的匹配关系。