起伏地形条件下长偏移距瞬变电磁三维正演
2022-06-22王新宇严良俊毛玉蓉谢兴兵
王新宇, 严良俊, 毛玉蓉, 黄 鑫, 谢兴兵, 周 磊
1.油气资源与勘探技术教育部重点实验室(长江大学),武汉 430100 2.非常规油气省部共建协同创新中心,武汉 430100
0 引言
随着地球物理电磁法正反演计算技术和软硬件的飞速发展[1-2],长偏移距瞬变电磁法(long-offset transient electromagnetic method, LOTEM)因其效率高、勘探深度大、应用范围广等特点,已成功应用于资源环境调查、剩余油和储层压裂动态监测及地热勘查等领域[3-8],应用效果良好。但地形地貌的复杂多样给LOTEM资料处理解释带来较大的困难[9],若不考虑起伏地形影响,很容易导致LOTEM资料解释错误。因此,研究LOTEM在起伏地形下瞬变电磁场的响应特征对实际资料处理解释具有重要指导意义。
电磁法勘探逐渐由粗放向精细发展,但电磁法数据的合理解释离不开有效的三维正反演算法。对此,已有大量学者对瞬变电磁正演算法进行研究[10-21]。Commer等[15]提出了一种并行时域有限差分算法,用于LOTEM电磁场响应的计算;Börner 等[16]提出一种有理Krylov方法,并基于矢量有限元在频率域求解Maxwell方程,通过频时转换得到时间域电磁响应;Um等[17]基于矢量有限元法,采用后退欧拉格式离散时间步长,并提出自适应步长加倍方法,采用直接求解器求解线性方程组,当步长不变时,仅需进行一次LU分解,大大加快了瞬变电磁三维正演速度;Börner等[18]提出使用高阶有理Krylov近似,结合直接求解器有效提高了地面瞬变电磁正演效率;Liu等[19]基于拟态有限体积法离散时间域电磁场方程,采用有理Krylov子空间方法计算时间域电磁场响应,实现地空瞬变电磁快速三维正演,并对比了该方法与隐式后退欧拉算法的计算效率;殷长春等[20]基于法向电流连续的自适应后验误差估计有效提高了瞬变电磁计算精度,并研究了海底起伏地形对时间域海洋电磁的影响;Liu等[21]基于有限体积法研究了LOTEM在各向异性地层中的电磁场响应特征。
近年来,勘探目标区域起伏地形等因素对电磁数据的影响规律越来越受到国内外学者的重视。Liu等[22]采用边界元法对航空瞬变电磁不同典型地形下的电磁场响应特征进行了数值模拟;Mitsuhata[23]基于有限元法,采用伪Delta函数分配偶极子源电流,并对起伏地形下LOTEM和可控源电磁法的电磁场响应特征进行对比分析;Zhdanov等[24]提出了非均匀背景电导率下复杂地电结构中的电磁法三维正演积分方程新算法,该算法在正演中引入地形等非均匀背景模型;强建科等[25]实现了三维起伏地形条件下直流电阻率法的有限单元数值模拟算法;董浩等[26]研究了起伏地形条件下交错网格有限差分法的大地电磁测深三维正演;Li等[27]基于矢量有限元法研究了复杂形状回线源瞬变电磁响应特征,并将其应用于复杂地形下任意形状回线源瞬变电磁三维正演;Lin等[28]采用交错网格有限差分法对可控源音频大地电磁法(CSAMT)在典型地形模型山峰、山谷地形下的电磁场响应进行了对比,说明地形对CSAMT电磁场响应影响剧烈;Li等[29]研究了复杂地质环境下电性源瞬变电磁场响应特征,但仅仅对磁场分量进行讨论,并没有研究电场分量受地形影响的程度;齐彦福等[30]研究了起伏地形对短偏移距瞬变电磁的影响,通过大量数值模拟,讨论了起伏地形对瞬变电磁响应的影响。
鉴于LOTEM在起伏地形下电磁场响应规律研究较少,本文基于矢量有限元法,通过Blender软件对起伏地质模型进行建模,采用开源网格剖分代码Tetgen[31]离散四面体网格,实现LOTEM三维正演模拟。并通过对层状模型与典型地电模型数值模拟结果的对比分析,验证算法的正确性和有效性。通过复杂不同三维模型算例,从理论上探讨地形对LOTEM电磁场的影响。
1 电磁场时域矢量有限元
1.1 电磁场矢量有限元控制方程
长偏移距瞬变电磁法满足的电场扩散方程为

(1)
式中:μ为磁导率;E(r,t)为t时刻r位置的电场矢量;Js(r,t)为t时刻r位置的长导线源电流密度;σ为电导率。
将模拟区域离散为互不相交的四面体,并引入矢量插值基函数,将自由度赋予在网格离散后的棱边上,在任意四面体单元e内,电场可展开为
(2)
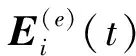
(3)
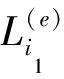
当方程(1)的E为近似解时,令方程(1)的残差矢量为
(4)
对于第e个四面体单元,确保其加权残差积分为0:
∭V(e)N(e)·G(e)dV=0。
(5)
式中:V(e)为第e个单元的体积;G(e)为第e个单元的残差矢量。利用Galerkin方法,并确保所有四面体加权残差总和为0,得到有限元控制方程:

(6)
式中:A为质量矩阵;E(t)为棱边上待求的电场值;B为刚度矩阵;S为外加激励源项。第e个四面体单元的质量矩阵A(e)、刚度矩阵B(e)的第(i,j)个元素和外加激励源项S(e)的第i个元素可表示为:
(7)
(8)
(9)
式中,σ(e)、μ(e)分别为第e个单元的电导率、磁导率。对于激励源,将长导线源分割为多段有限长度的电偶极子,将其置于四面体的棱边上,且电流密度方向平行于棱边,每个电偶极子的电流密度可表示为[32]
Js(r,t)=δ(r-rs)pI(t)dl。
(10)
式中:δ为脉冲函数;rs和dl分别为电偶极子的空间位置和长度;p为电流方向;I(t)为t时刻的电流强度。利用脉冲函数的筛选性质,S可表示为

(11)
1.2 初值问题及边界条件
LOTEM一般采用下阶跃激励。下阶跃激励的初始电场由以下两部分组成[15]:
(12)

(13)
设点源电流强度为I,位于rs=(xs,ys,zs)处,利用微分形式的欧姆定律j(r)=σE(r),根据电场连续性得到[33]
·j(r)=Iδ(r-rs)。
(14)
式中,j(r)为位置r处的电流密度。联立式(13)和式(14)可得到点源场满足的三维Poisson方程:
·(σφ(r))=-Iδ(r-rs)。
(15)
对直流电场和时域电磁场采用相同的网格来保证直流电场与矢量电场边界的一致性,且直流场问题与时域电磁场问题均采用总场方法求解。由于求解区域较大,在计算过程中对外边界Γ均施加Dirichlet边界条件:
φ|Γ=0;(n×E)|Γ=0。
(16)
式中:Γ为计算区域的外边界;n为Γ的单位外法向向量。
2 LOTEM三维正演实现
2.1 非结构化网格建模
电磁场有限元前处理是有限元数值模拟的重要部分,正确且合理的有限元模型以及布局合理的网格密度、质量可以有效提高数值精度与计算速度。本文采用Blender开源软件建立复杂地质模型。首先将高程数据导入Blender软件进行起伏地形三维建模,生成三维模型文件*.ply。该文件格式简单,仅仅需要顶点元素列表与面元素列表即可实现空间模型表面网格离散。应用开源代码Tetgen识别模型文件并进行非结构四面体网格离散(图1)[31]。对于起伏地形的四面体网格剖分,除发射源、测点与异常体局部加密外,对研究区域地形也要采用相对较小的网格,以保证数值模拟精度。
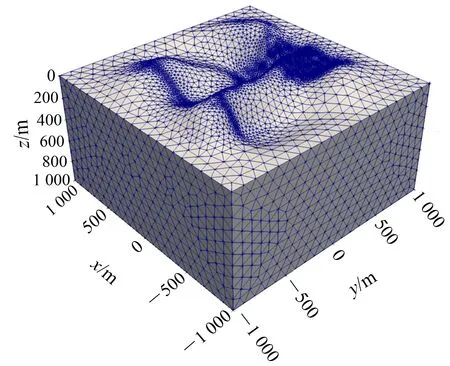
图1 Tetgen起伏地形网格剖分示意图
2.2 线性方程组建立及求解
为提高数值精度,采用二阶后退欧拉差分格式对时间进行离散[15]:

(17)
式中:E(k)(t)为k时刻的电场解向量;Δt为k时刻前两道时间步长。将式(17)代入式(6)可得
(3A+2ΔtB)E(k)(t)=
A[4E(k-1)(t)-E(k-2)(t)]-2ΔtS(k)。
(18)
最终形成大型线性方程组,可表示为
KE=b。
(19)
本文使用直接求解器Pardiso[34]对式(19)进行直接求解。对于时域电磁场矢量有限元问题,当Δt不变时,方程(19)左端系数矩阵K固定不变,只需对其进行一次LU分解,将右端项回代求解,可有效提高计算效率。本文正演模拟均在处理器为AMD Ryzen 9-5950、内存为96 GB的工作站运行。
3 数值算例
3.1 三维正演算法验证


图2 层状地层下垂直接触带复杂三维模型
为验证层状模型的计算精度,将上述模型基底电阻率设为100 Ω·m,计算层状地层的电磁场响应,结果如图5所示。由图5c可知,相对误差在局部急剧增大,这是由于数值方法均会产生一定的直流偏移,虽然该偏移对整体精度影响较小,但变号处电磁场数量级一般都很小,直流偏移对变号处电磁场的影响较为严重,导致变号处误差较大,这在LOTEM正演模拟过程中难以避免。但dBz/dt与Ey的数值解与解析解整体拟合良好,误差基本被控制在3%以内。进一步说明了本文算法有效性,可进行LOTEM起伏地形条件下的电磁场数值响应规律分析。
3.2 山脊地形LOTEM三维正演
为研究起伏地形下LOTEM电磁场的响应特征,建立如图6所示的水平地表和山脊地形模型。山脊地形基底长和宽均为1 000 m,高度为50 m,顶部长宽均为500 m,发射源长度为200 m,沿y方向布设,中心点坐标为(-2 000 m,0 m,0 m),发射电流1 A;地表测点、测线间距均为100 m,共21×21=441个测点;围岩电阻率为100 Ω·m,在水平地表下存在一个电阻率为10 Ω·m的异常体,大小为400 m×400 m×200 m,顶面埋深200 m;分别计算水平地表与山脊地形模型在测点处的电磁场响应。将长导线分割为100段电偶极子;在发射源和测点处局部加密网格,水平地表最终生成1 456 233个网格, 233 004个节点,1 692 179条棱边;山脊地形最终生成1 464 446个网格,234 444个节点,1 701 832条棱边;水平地表模型正演占用内存11.4 G,求解耗时2 183 s,山脊地形模型正演占用内存11.2 G,求解耗时2 214 s。

a. 加密区域;b. 扩边区域。
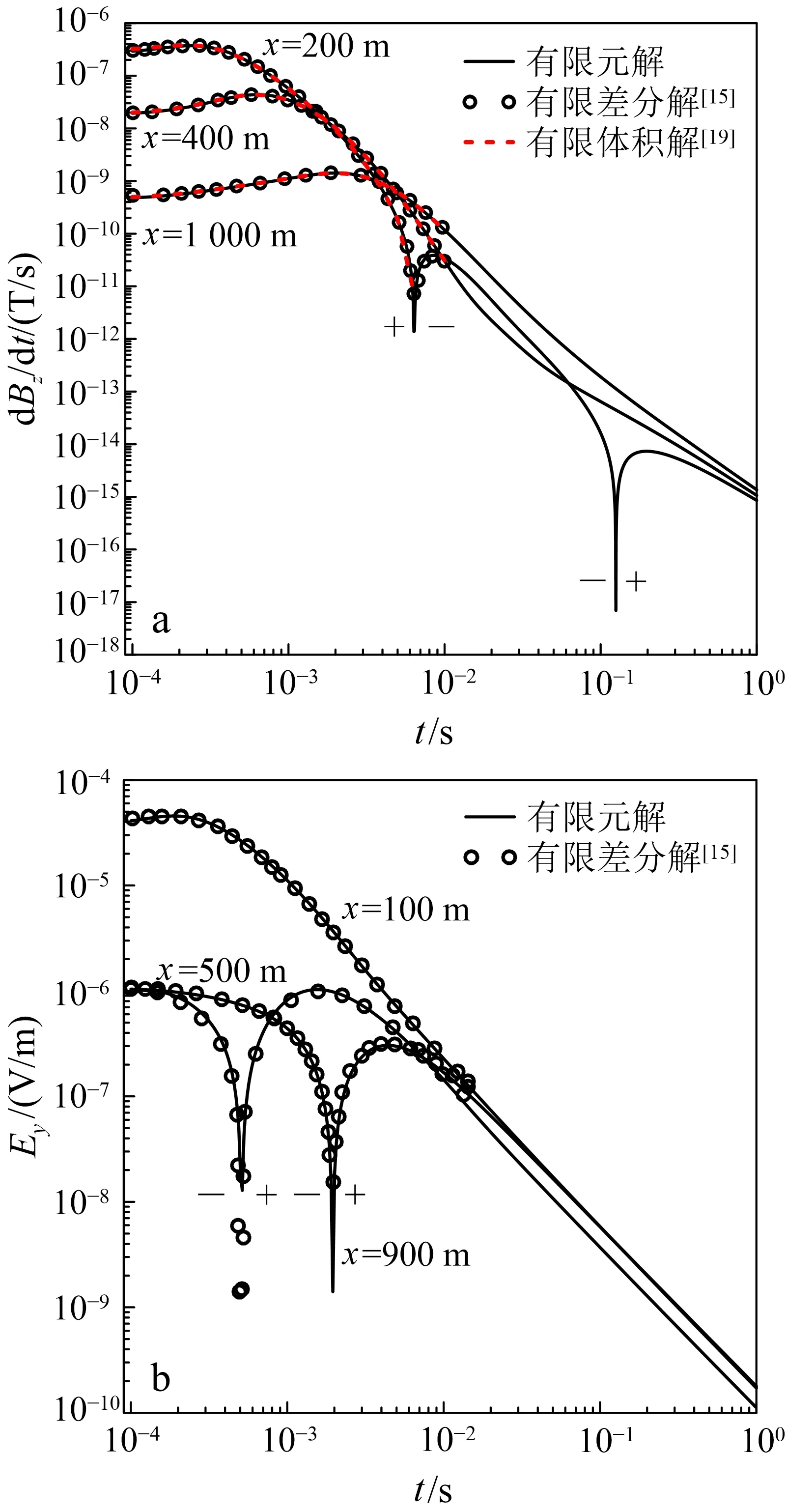
图4 不同方法的数值结果对比
图7为水平地表和山脊地形模型在测点处不同时刻电场分量的等值线图。对于有耗介质,电磁波在高阻介质中衰减快,在低阻介质中衰减慢。但随着时间的推移,电磁波在有耗介质中传播,电场整体逐渐衰减。图7中10 μs到10 ms之间,感应电流主要集中在发射源附近,靠近发射源一侧的电场较大,不满足平面电磁波扩散。随着时间的增加,感应电流扩散范围逐渐增大,在100 ms后,地表测点电场分布较为均匀,近似满足平面电磁波扩散。对于水平地表模型的电场响应(a1—f1),异常体的范围被很好地反映出来。由于低阻异常体埋深较浅,对于山脊地形模型的电场响应(a2—f2),虽然Ey可以反映出异常区域的存在,但受地形的影响,在地形周围会出现假异常,且异常响应范围明显大于水平地表模型的异常响应范围。可见,起伏地形会影响LOTEM的观测数据对地下目标体的判别,若不考虑地形因素,势必会给实际资料解释带来困难。
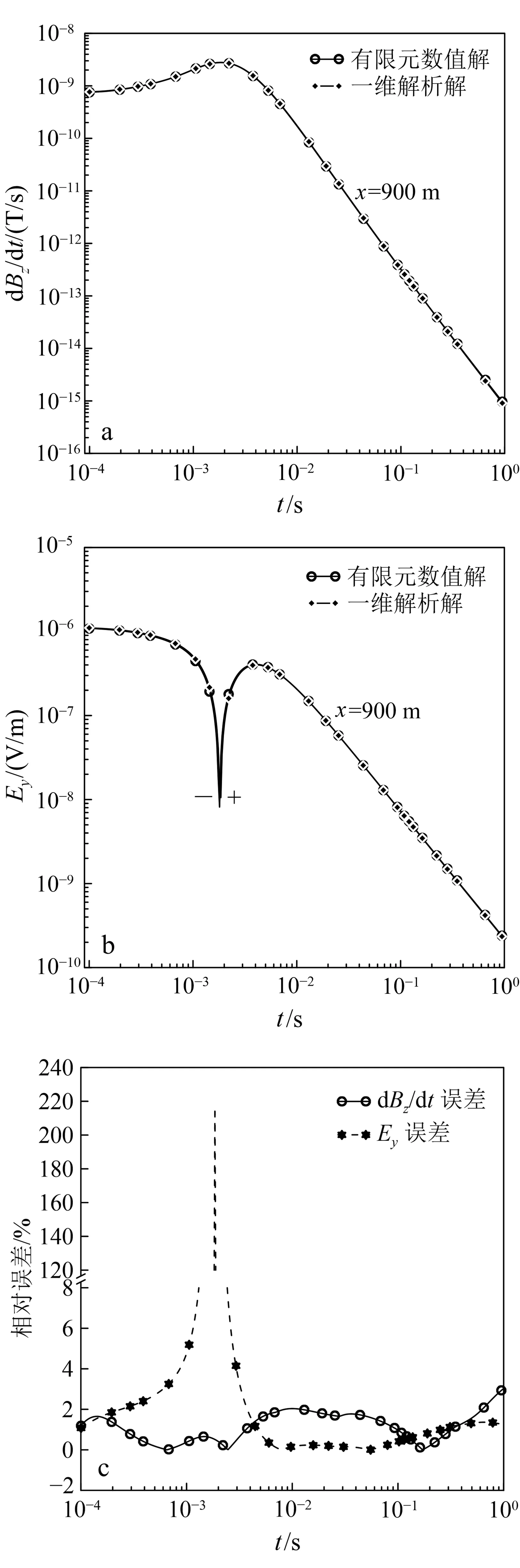
图5 基底电阻率为100 Ω·m时的数值解与解析解对比
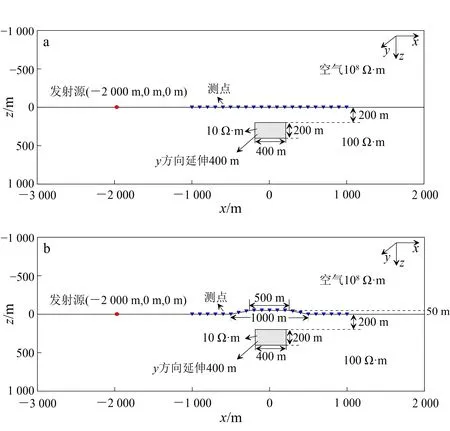
图6 水平地表(a)和山脊地形(b)模型
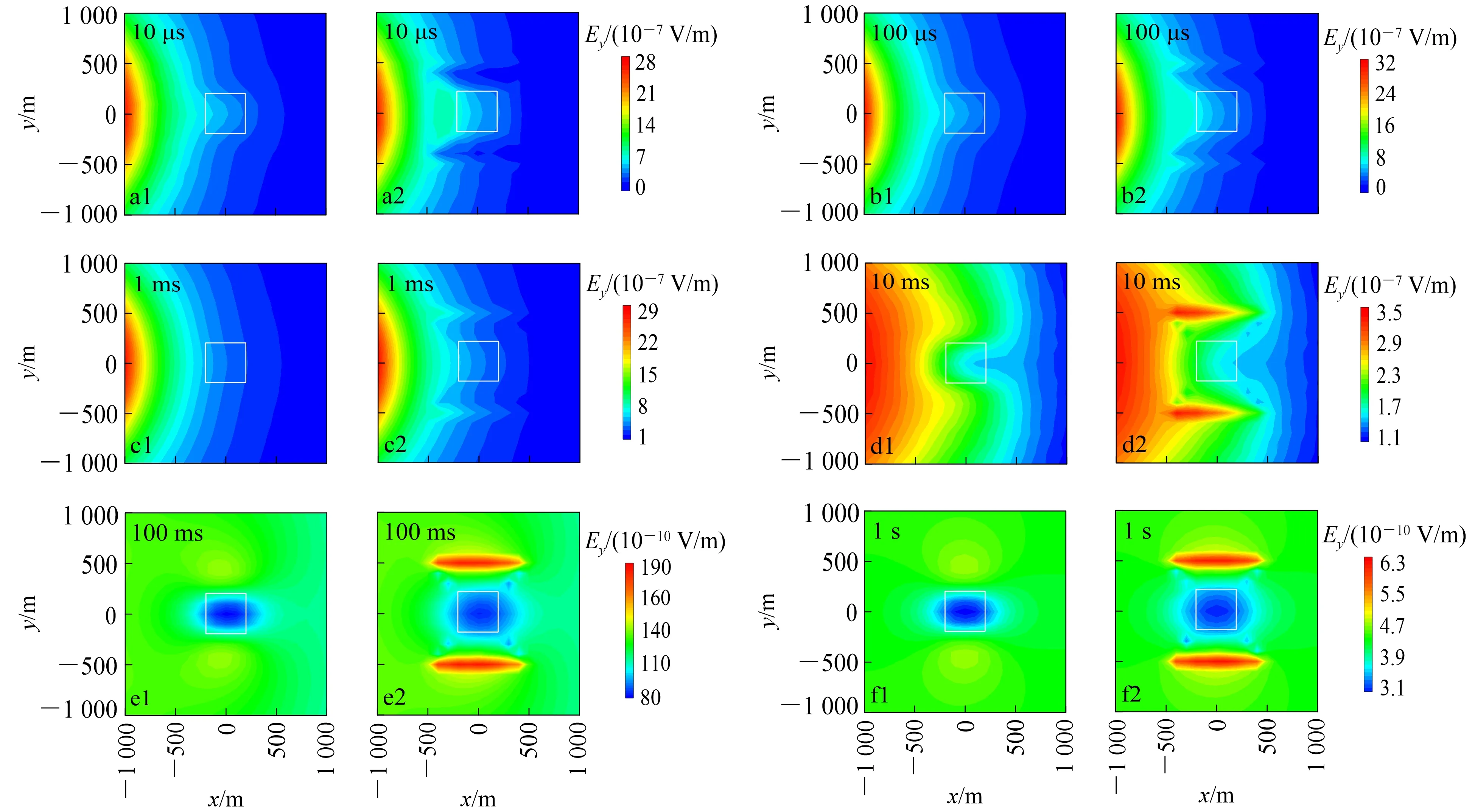
a1—f1. 水平地表;a2—f2. 山脊地形。
3.3 复杂地形LOTEM三维正演
为研究复杂地形下LOTEM电磁场的响应特征,设计如图8所示模型。试验区最高海拔为132 m,最低海拔为-68 m,发射源所在海拔为0 m,发射源长度为1 000 m,沿y方向布设,中心点坐标为(-1 200 m,0 m,0 m),发射电流1 A;y方向的测线位于x=0 m处,测线总长度1 000 m,共41个等间隔测点(图8a)。浅地表第一层覆盖层的最大厚度为221 m,最小厚度为41 m,电阻率为100 Ω·m;第二层覆盖层厚度350 m,电阻率为50 Ω·m;基底围岩电阻率为100 Ω·m;在第二层覆盖层和基底中嵌入一个电阻率为10 Ω·m或者1 000 Ω·m的阶梯状异常体,该异常体由3个400 m×100 m×200 m的长方体构成,异常体的整体高度为400 m,顶部埋深100 m,y方向正负各延伸200 m;x方向长度为300 m(图8b)。将长导线分割为400段电偶极子,在发射源和测点处局部加密网格(图8c),最终生成2 777 110个四面体网格,442 984个节点,3 220 869条棱边。计算区域整体尺寸300 km×300 km×200 km,空气层厚度为50 km;该模型正演占用内存32.8 G,求解耗时10 283 s。
图9为高阻和低阻阶梯状异常体在地表测线的电场响应结果,受地形因素的影响,无论异常体为低阻还是高阻,其异常响应基本被“埋没”。
为进一步研究LOTEM对低阻、高阻异常体的响应机理,绘制图10所示地下电场分布及电流密度矢量图。由于起伏地形和地下目标体的相互耦合作用,使测线附近的电场响应发生了严重的畸变;随着时间的增加,在有耗介质中,电场不断衰减,可以清晰地看出涡流不断向下传播的过程。由图10a、c、e、g可以看出,由于低阻异常体对电流的吸引作用,感应电流在低阻异常体中产生明显的电流通道效应,根据电流密度法向连续条件,低阻异常体的电导率较高,感应的电场值较小。反之,对于高阻异常体的电场响应(图10b、d、f、h),电流在高阻异常体周围产生明显的电流通道效应,高阻异常体的电导率较低,感应的电场值较大。
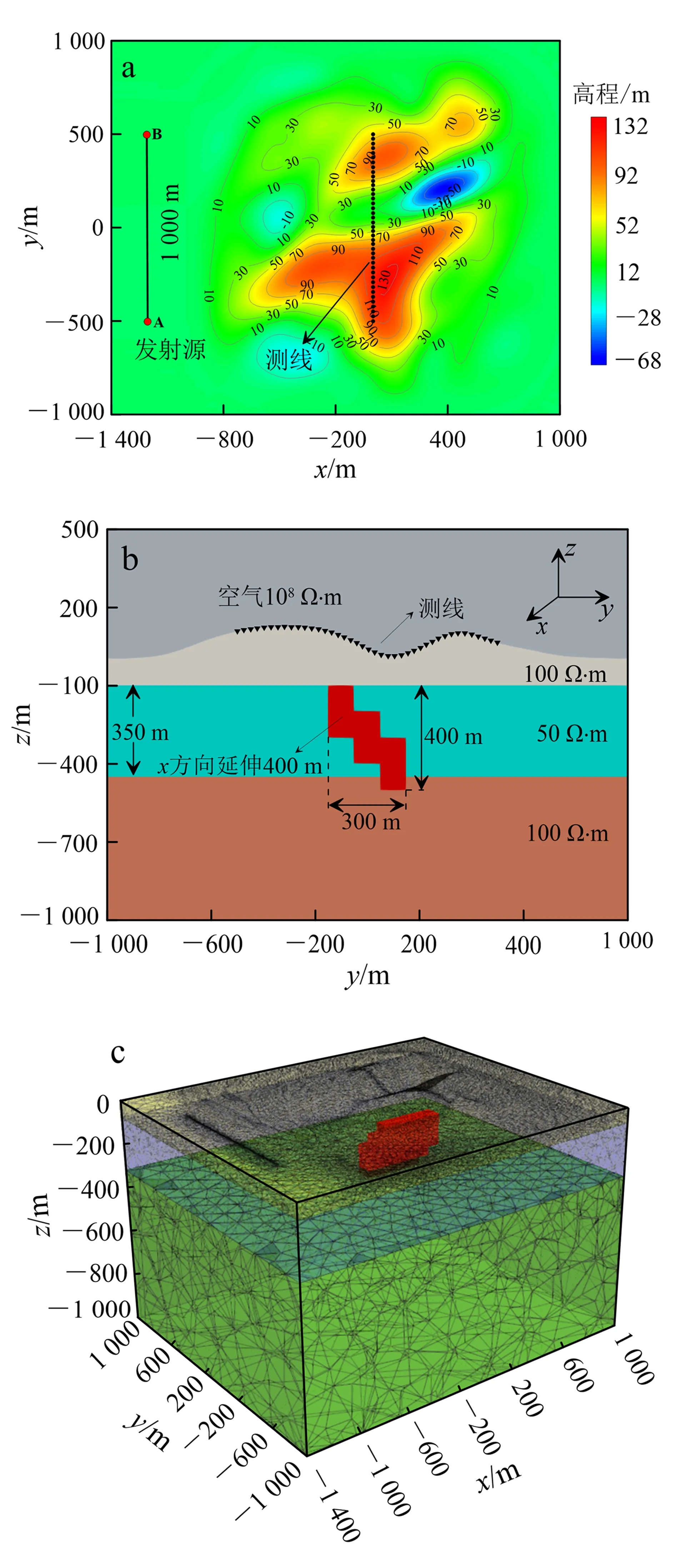
a. 试验区等高线;b. 模型yz切面;c. 网格剖分。
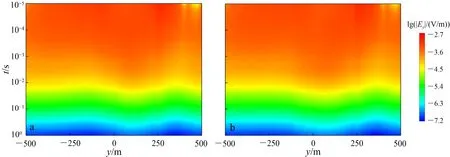
a. 低阻异常体;b. 高阻异常体。

a、c、e、g. 低阻异常体;b、d、f、h. 高阻异常体。
4 结论
本文通过Blender软件和开源代码Tetgen实现起伏地形复杂地质模型建模及四面体网格剖分,并基于非结构矢量有限元法实现了长偏移距瞬变电磁(LOTEM)三维正演模拟。通过大量数值模拟得出以下结论:
1)通过与解析解、时域有限差分解、有理Krylov方法的拟态有限体积解的精度对比分析,验证了本文算法正确性和有效性,微弱的直流偏移虽然对整体计算精度影响较小,但会导致电场变号位置的误差急剧增大,因此,在数值模拟或者实际资料处理解释中,变号附近的场值一般不予考虑。
2)针对起伏地形条件下复杂地电模型LOTEM的电磁响应特征进行分析,表明起伏地形对LOTEM电磁响应影响较大,会“削弱”甚至“埋没”异常体的电磁响应,从而无法对异常体的位置和电性特征进行有效分辨。
3)通过对地下电场的等值线及电流密度矢量分布图研究,由于地形与异常体的相互耦合作用,测线附近的电场畸变严重,使得地表的观测电场难以对地下目标体进行有效判别。
整体研究表明,起伏地形对LOTEM电场响应影响较大,在实际勘探中地形效应不可忽略。针对以上问题,我们下一步将展开地形校正的研究或开发反演算法,直接将地形因素考虑到LOTEM的三维正反演中。
