冗余机器人喷涂系统改进人工鱼群逆运动学求解算法
2022-06-22刘雪梅李爱平卢军国
刘雪梅 冯 焱 杨 振 李爱平 卢军国
1.同济大学机械与能源工程学院,上海,2018042.上海外高桥造船有限公司,上海,200137
0 引言
随着我国对船舶建造质量、效率和环保等因素的愈发重视,船舶制造业智能化转型升级的需求日益迫切。2020年,工信部发布《船舶总装建造智能化标准体系建设指南(2020版)》,其中明确指出船舶分段机器人喷涂装备为其重要建设内容之一[1]。不同于在汽车、家电等行业已广泛应用的机器人系统,船舶工业的作业对象尺寸远大于机器人,且标准化程度较低,给机器人的应用带来了挑战[2]。为了在扩展工作空间的同时也能更好地避开机器人的奇异位型和关节极限,冗余机器人被越来越多地应用于船舶、航空航天等领域[3-5]。如何快速获取高精度的逆运动学解成为了冗余机器人研究的重要课题[6]。
YANG等[7]根据对7自由度拟人机械臂构型的分析,采用代数方法先求得中间关节的值,再以此为约束条件分别求取另外6个关节的值,这种解析法快速而精确,然而只适用于前3个关节与后3个关节各自等效为球形关节的机器人。廖柏林等[8]结合最小速度范数方案及最小加速度范数方案,使用雅可比矩阵伪逆的方法来控制冗余机械臂运动,该方法实现简单,但在靠近机器人奇异位型时关节速度容易超出极限。BENZAOUI等[9]采用任务扩充法将避障作为附加约束条件使机器人雅可比矩阵扩展为方阵,使得逆运动学具有确定解,然而使用增广雅可比矩阵求取逆解依然可能导致奇异位型速度超限。刘世平等[10]使用BP神经网络得到了Baxter 7自由度机械臂逆解,但神经网络方法需要训练,大量样本的获取是一个实际问题。针对这些不足,越来越多的学者将智能仿生算法应用于冗余机器人逆解问题,包括差分进化(differential evolution, DE)算法[11]、量子粒子群(quantum behaved particle swarm optimization, QPSO)算法[12]、天牛须搜索(beetle antennae search, BAS)算法[13]、人工蜂群(artificial bee colony, ABC)算法[14]和萤火虫群(glowworm swarm optimization, GSO)算法[15]等,都取得了较好的求解效果。
人工鱼群算法(artificial fish swarm algorithm, AFSA)作为一种新型仿生算法具有收敛速度快、全局搜索能力强等优点,已成功应用于多个领域[16-18],但算法求解精度会随迭代次数下降[19],因此,本文以船舶分段机器人喷涂系统为研究对象,提出一种改进人工鱼群算法(improved artificial fish swarm algorithm, IAFSA)以解决冗余机器人逆运动学问题。
1 问题描述
1.1 机器人运动学建模
本文采用图1所示冗余机器人喷涂系统来完成船舶分段非结构面的喷涂工作。该系统主要由一个3移动自由度桁架和一台6转动自由度史陶比尔RX160L机器人组成。其中,桁架作为外部轴极大地扩展了工作空间,其移动范围长宽各30 m,高12 m,史陶比尔RX160L机器人横向安置在可沿竖直方向移动的平台上,机器人末端并列安装两个高压无气喷枪以提高喷涂效率。
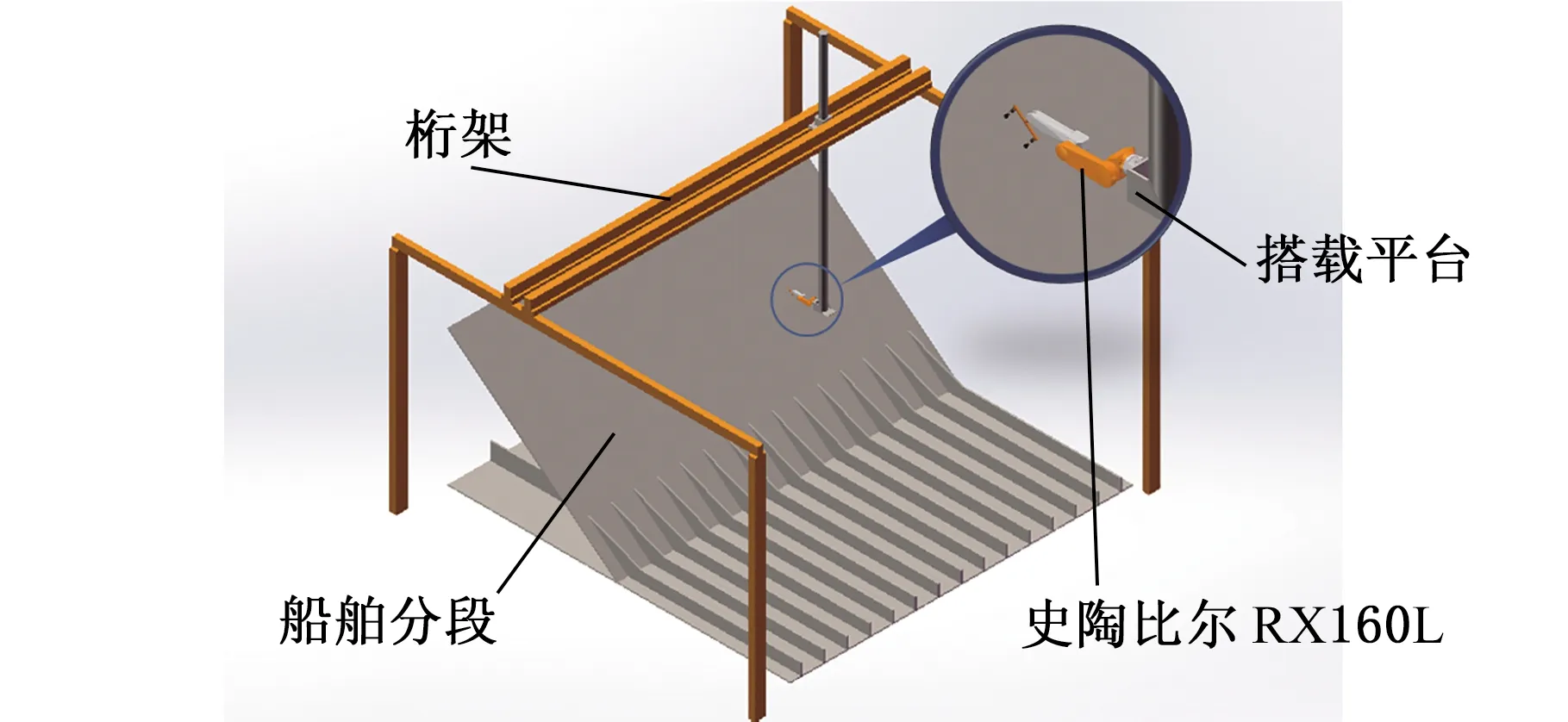
图1 冗余机器人喷涂系统
本文采用改进DH参数法(modified DH, MDH)建立机器人系统的运动学模型[20]。由于机器人模型搭建在SolidWorks环境中,故选取SolidWorks模型空间原点建立基坐标系。基于MDH参数法得到机器人系统各关节上的坐标系,如图2所示,MDH参数表如表1所示,其中ai-1、αi-1、di、θi分别代表各连杆和运动副的连杆长度、连杆转角、连杆偏距以及关节角。
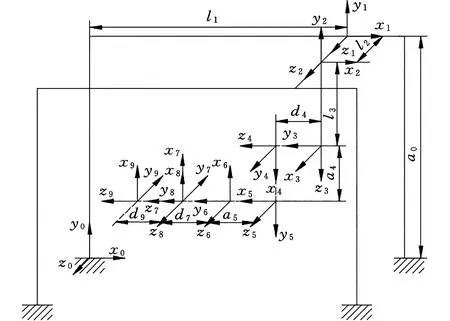
图2 机器人系统坐标系

表1 机器人系统MDH参数

(1)
式中,c、s分别表示cos和sin。
由此,机器人末端执行器的坐标系相对于基坐标系的位姿变换关系可表示为
(2)
其中,rij为姿态矩阵;pk为位置矩阵,解析式如下:
(3)
本文所用的机器人系统a0=20 750mm,a4=150 mm,a5=825 mm,d4=997.70 mm,d7=925 mm,d9=109 mm。
1.2 逆运动学问题优化模型的建立

本文以机器人各关节运动范围为约束条件,以末端执行器位姿求解值与期望值的误差最小以及关节行程长度最小为优化目标,建立逆运动学问题的优化模型如下:
(4)
其中,上标撇表示数据通过x′=(x-xmin)/(xmax-xmin)进行了归一化处理,下标d、s分别表示期望值和初始值,rij与pk的最值可根据式(4)由式(3)求得;由于移动关节行程巨大,故设置系数η=100以削弱归一化对绝对位置误差造成的影响;λ为关节行程权重,为优先保证位姿准确,本文取λ= 0.01。
2 改进的人工鱼群算法
2.1 人工鱼群算法
人工鱼群算法由李晓磊等[21]在2001年提出,其基本思想是在一片水域中,鱼的数量存在最多的地方往往就是这片水域里营养物质浓度最高的地方,根据鱼群的这一生活习性来模仿其行为,进而寻找最优解。假设人工鱼的数量规模为N,其中第i条人工鱼Xi=(x1,x2,…,xm)为第i个解,m为解的维度,营养物质浓度表示为目标函数值Yi=f(Xi)。寻优过程中人工鱼的视野范围为V,其移动步长为S,区域拥挤度因子为δ,寻优最大尝试次数为t,第i条与第j条人工鱼之间的距离以它们的欧几里得范数表示,即dij=‖Xi-Xj‖。鱼群活动由觅食行为、聚群行为和追尾行为三种行为组成。
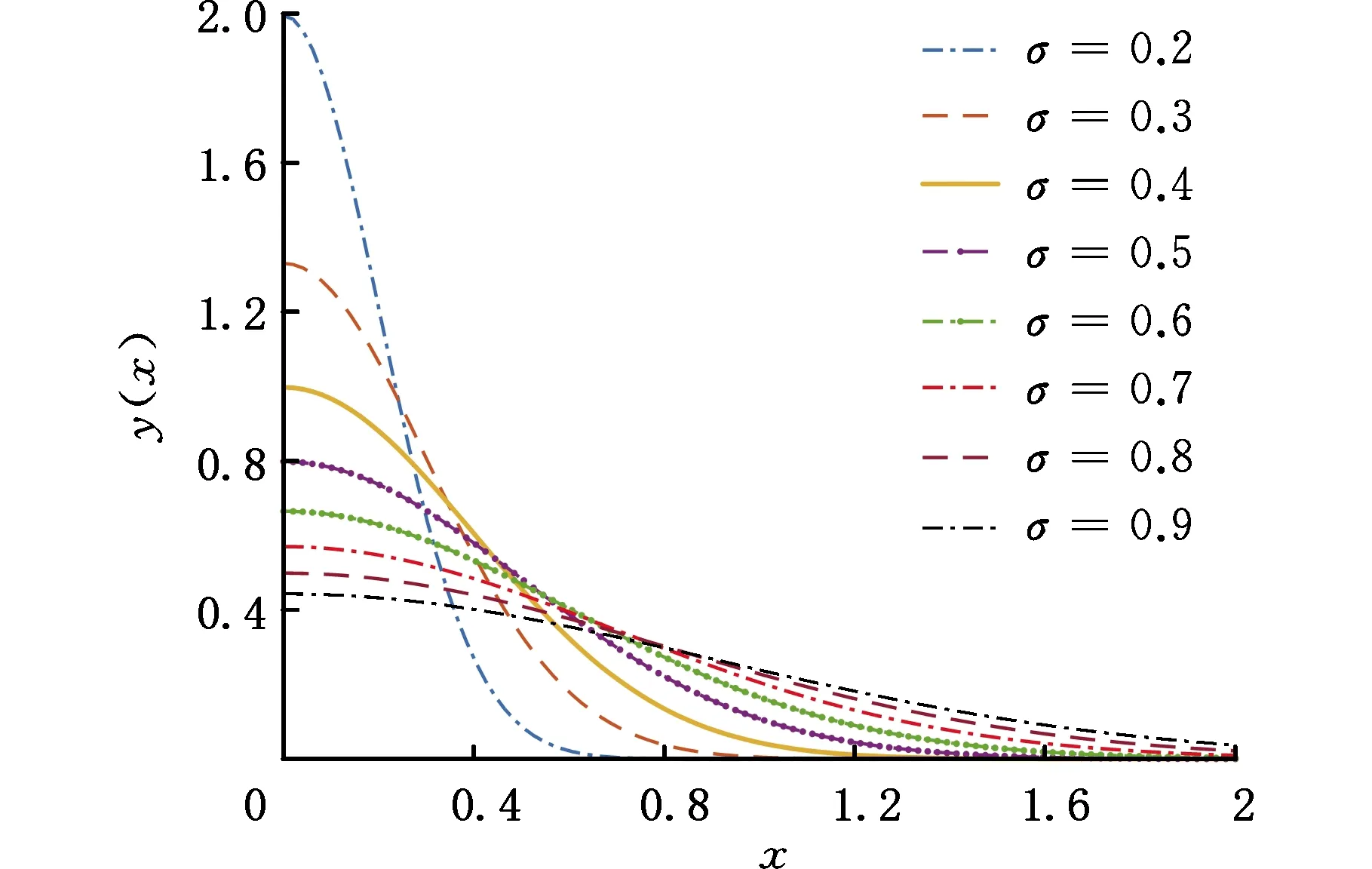
(1)觅食行为。假设当前状态下有人工鱼Xi,其目标函数值为Yi,在此鱼的视野范围内随机选择一条人工鱼Xj,其目标函数值为Yj。在求最小值问题上,如果Yj (5) 式中,Im为随机方向上的单位向量。 (2)聚群行为。搜索人工鱼Xi的视野范围内所有人工鱼的数量nf以及视野中心位置Xc。如果Yc/nf<δYi,说明视野中心状态更优且不太拥挤,则人工鱼Xi向中心位置Xc移动一个步长;否则,执行觅食行为。移动计算公式为 (6) Yc/nf<δYi (3)追尾行为。搜索人工鱼Xi视野范围内最优人工鱼Xbest。如果Ybest/nf<δYi,则人工鱼Xi向最优人工鱼Xbest移动一个步长;否则,执行觅食行为。移动计算公式为 (7) Ybest/nf<δYi 人工鱼群算法有着较好的全局搜索能力和收敛速度,但其中人工鱼的搜索视野和移动步长是固定值,制约了算法性能的进一步提高。在基本人工鱼群算法中,较大的视野范围会使人工鱼群的三种行为影响更突出,在增强算法全局搜索能力的同时也增加了计算量,延长了计算时间;较小的视野容易使算法陷入局部最优。而当移动步长取值过大时,算法在后期容易错过目标函数的峰值或谷值,导致其在真正的最优解附近振荡,造成最终解的精度下降;若移动步长过小,算法的收敛速度会大大降低。为了克服以上弊端,本文在算法执行过程中引入基于正态分布的视野和步长动态调整策略,即 式中,Vmax为视野上限;Vmin为视野下限;Smax为步长上限;Smin为步长下限;g为当前迭代次数,gmax为最大迭代次数;σ为正态分布的标准差。 图3 正态分布曲线 在迭代初期,搜索空间很大,算法以一个较大的视野和步长快速搜寻整个解空间,以保持良好的全局搜索能力和收敛速度;随着迭代继续,搜索空间逐渐收缩至若干个特定区域,视野和步长快速衰减的同时保留了一定跳出局部最优的能力;在迭代后期,视野和步长的衰减速度再次趋缓,在一个较小的水平上密集搜索局部区域内的解,以提高最终解的精度,改善算法的局部搜索能力。 改进后的人工鱼群算法流程如图4所示。 图4 IAFSA算法流程图 本实验根据给出的机器人末端执行器期望位姿以及机器人初始状态来求解机器人各关节的转角及位移,实验环境为MATLAB 2018b, Win10 Intel(R)Xeon(R)W-2135 CPU @ 3.70GHz。随机给出机器人末端执行器期望位姿为 设置机器人初始状态,即各关节初始转角及位移为(0,0,0,0,0,0,0,0,0)T。采用基本AFSA算法、混合改进人工鱼群算法(HIAFSA)[22]与本文提出的IAFSA算法进行比较,三种算法的参数设置如表2所示。 表2 三种算法的参数设置 每种算法各运行10次,每次迭代500代,对实验数据取平均值,结果如图5和表3所示。 图5 三种算法的目标函数值收敛曲线 表3 三种算法的求解效果对比 可以发现,三种算法最终都能取得较为理想的求解效果。由图5可以看出,IAFSA算法的收敛速度要优于HIAFSA和AFSA算法。由表3可以得到,IAFSA算法的目标函数值较AFSA降低了27.91%,较HIAFSA降低了20.03%,显著减小了机器人末端执行器位姿求解值与期望值之间的误差,提高了逆解的精度;IAFSA算法计算时间较AFSA缩短了4.41%,较HIAFSA增长了2.91%,在原有算法的基础上进一步提高了计算速度,但略微慢于HIAFSA。综合比较,本文提出的IAFSA算法具有更好的搜索能力和收敛速度以及相对较快的计算速度。 现以图1中船舶分段的倾斜平板为例,在SolidWorks Motion环境中以“弓”字形轨迹对其进行喷涂仿真,对机器人各关节添加马达,选用IAFSA和HIAFSA算法对喷涂轨迹点位姿矩阵进行求解,将结果以数据点的形式输入各关节马达,驱动机器人完成喷涂动作。使用Motion的图解功能跟踪机器人末端执行器的位姿,前20个轨迹点末端的位姿误差如图6所示,其中为了简化对姿态的描述,假定末端执行器坐标系以基坐标系为固定参照系,先绕x轴旋转γ角,再绕y轴旋转β角,最后绕z轴旋转α角,以表征姿态矩阵rij。 (a)x方向位置误差 (b)y方向位置误差 从仿真结果可以看出,IAFSA算法得到的位姿误差曲线较HIAFSA明显更为平稳且绝对值更小,以图6b为例,IAFSA计算得到的y方向位置误差平均值为-0.0615 mm,标准方差为0.2054;HIAFSA得到的平均值为-0.3404 mm,标准方差为1.298,分别为IAFSA计算结果的5.5倍和6.3倍。另外,HIAFSA在第12、19轨迹点上分别达到1.712 mm和-5.396 mm的误差峰值和谷值,远超过了IAFSA的最值0.373 mm和-0.550 mm。由此可见,IAFSA算法较HIAFSA算法得到的机器人末端执行器的逆运动学解精度更高、平稳性更好,其位置误差始终小于1 mm,姿态误差小于1°,满足喷涂要求,验证了所求逆解的正确性和方法的有效性。 (1)针对一种由3移动自由度桁架和6转动自由度机器人组成的船舶分段机器人喷涂系统,通过MDH参数法建立了其运动学模型并得到了运动学正解。 (2)提出了一种基于正态分布衰减视野及步长的改进人工鱼群算法(IAFSA),以姿态误差最小和关节行程最短为目标求解冗余机器人逆解问题。实验对比结果表明,IAFSA算法保持了良好的全局搜索能力和收敛速度,并改善了最优解精度和计算时间,强化了局部搜索能力。 (3)逆解的精度和误差稳定性通过SolidWorks Motion模块仿真得到了验证,证明了IAFSA算法在冗余机器人逆运动学求解问题中的有效性。2.2 基于正态分布的视野及步长动态调整策略
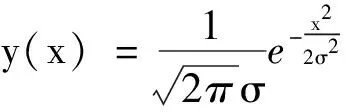

3 仿真实验



4 结论
