压电驱动微型精密夹持机构设计与实验研究
2022-06-22童玉健方记文
李 冲 童玉健 梁 康 钟 伟 方记文
江苏科技大学机械工程学院,镇江,212100
0 引言
压电智能材料因具有结构简单、响应速度快、定位精度高等优点而越来越受到社会的关注。压电作动器被成功应用于微纳米定位[1-2]、生物医学工程[3-4]、航空航天[5]等领域。
精密夹持是关于压电驱动的一大应用,涌现出了众多研究成果。RUIZ等[6]设计了一种压电微型夹持器,该夹持器为非对称分层结构,加工制造难度较大,他们采用拓扑优化法对夹持器进行了最优设计。LOFROTH等[7]研制了一种用于多对象操作的模块化夹持器,该微夹持器将传统的加工技术与MEMS技术相结合,形成了一个由铝基和可替换的末端执行器组成的模块化机构。MEHRABI等[8]采用实验设计的方法设计并改进了一种采用压电驱动器的微夹持器,该夹持器的创新之处在于,弯曲的压电陶瓷驱动器与微夹持器通过刚性楔连接。DAS等[9]采用单级位移放大机构设计了低连带运动的压电夹持器。微夹持机构实现了较高的定位精度、高位移放大比和大输出位移。
国内学者在压电夹持机构方面也进行了一系列的研究。针对微夹持器的大行程、低耦合等要求,林超等[10]采用桥式机构和杠杆机构设计了一种新型三级放大的压电驱动微夹持器,通过实验测试,该夹持器位移是原来的19.7倍,工作行程达到750 μm。为了实现对微纳尺度下物件的精密夹持,吴志刚等[11]利用柔性铰链设计方法设计了一种柔性微夹钳系统,利用PID控制算法对微夹钳系统进行实验控制,结果显示跟踪控制结果误差和放大比分别为2.4%和9.12,能够满足微尺度下的夹持工作。赵建宇[12]研制了一种基于平行四边形柔性机构的集成微装配力、夹持力和夹爪位移传感器的压电致动微夹钳,能够实现装配力、夹持力和夹爪位移的高精度实时检测。此外,针对对称夹钳容易造成受力不均的问题,陈晓东等[13]设计了一种基于复合柔性铰链的非对称压电微夹钳,该微夹钳在150 V电压驱动下可实现160.97 μm的输出位移,当输入力为3 N时,输出夹持力为1.23 N。
虽然在压电精密夹持领域已经取得了众多研究成果,然而大多数已有成果存在结构复杂、加工制造工艺复杂、成本较高等缺点。鉴于此,本文提出一种新型压电驱动微型精密夹持机构,该机构由两个柔性铰链构成的夹持臂构成,具有结构简单、制造成本低等优点。
1 压电精密夹持机构工作原理
压电精密夹持机构结构如图1所示,由两个夹持臂构成,夹持臂头部呈弯折状,与被夹持物体的接触处为圆弧状,可增大与被夹持物体之间的接触面积,夹持臂通过柔性铰链与夹持机构外框连接。压电叠堆末端设置预紧螺钉,以此来对压电叠堆施加预紧力。
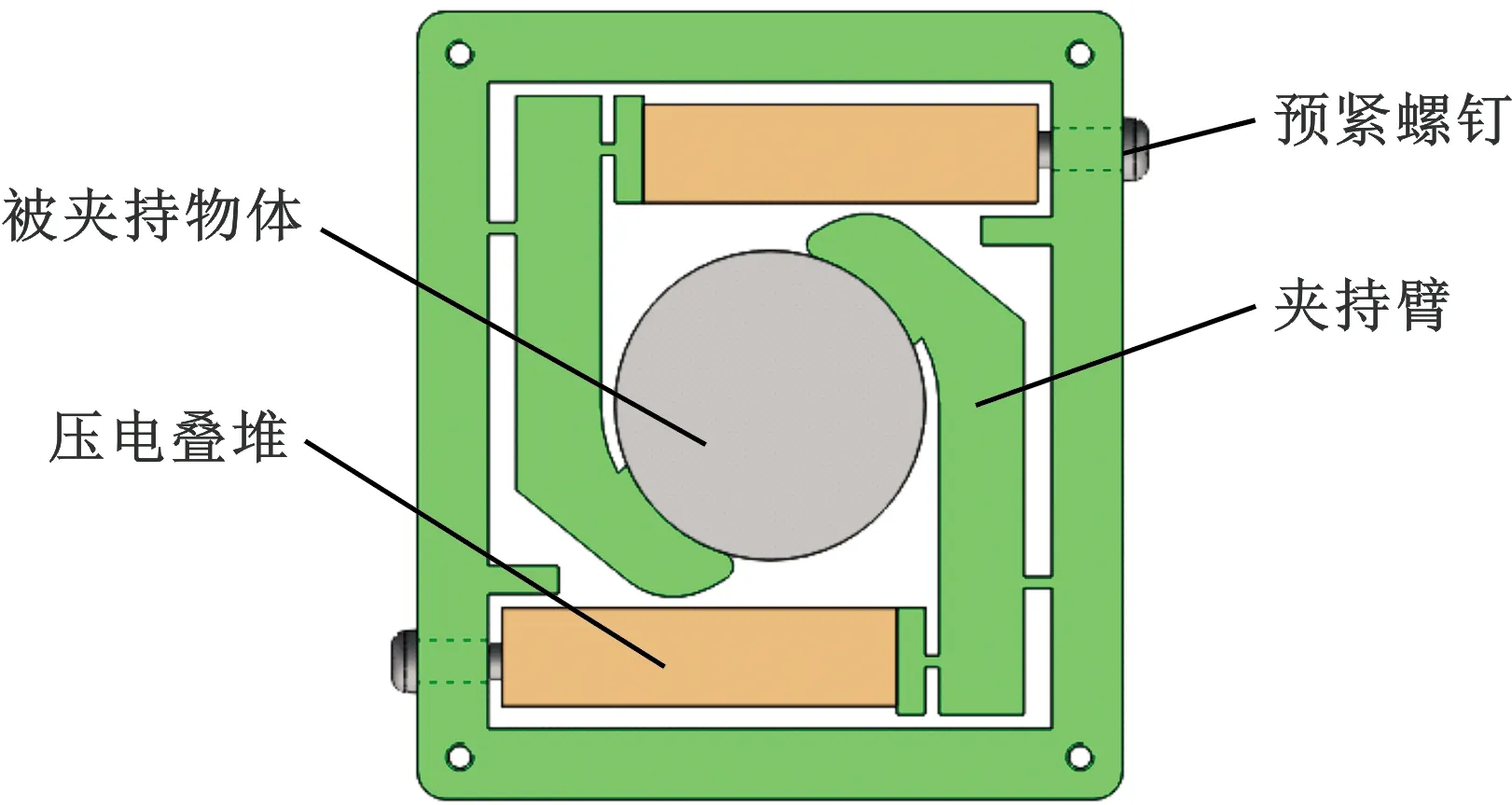
图1 压电精密夹持机构结构
图2是压电精密夹持机构的工作原理图,夹持机构由两个压电叠堆提供驱动。压电叠堆未施加电压时,两个压电叠堆处于原长,夹持臂与被夹持物体之间存在一定间隙。当对压电叠堆施加驱动电压Up时,压电叠堆产生变形量δp,变形量迫使夹持臂绕柔性铰链旋转一定角度,此时,两夹持臂将被夹持物体夹紧。

图2 夹持机构工作原理图
在夹持机构工作过程中,被夹持物处于静止状态,不发生旋转运动,本文中夹持机构输出的是夹持臂的位移和力,用于将目标物夹持住。在实际应用时,夹持机构抓住目标物后可随基体移动。本文主要研究作为执行机构使用的夹持机构,不涉及基体的移动,夹持机构在实际使用时可配合机械臂等机构工作。
2 压电精密夹持机构输出特性
压电夹持机构利用压电叠堆提供动力,由于压电迟滞效应的存在,压电叠堆输出应变随电压呈非线性变化,根据压电学理论,压电叠堆的截面应变关系[14]为
(1)
(2)
式中,s33、d33、d333分别为压电叠堆的弹性柔度系数、压电应变常数和非线性压电应变常数;Sp为横截面积;P为预紧力;lp为单层压电陶瓷片的厚度;b1~b4为常系数;U0为最大激励电压;ε0为激励电压U0下的非线性应变;εp为驱动电压Up下的非线性应变。
由力和应变的关系可得压电叠堆在电压驱动下的输出力
Fp=EpSpεp
(3)
式中,Ep为压电叠堆的弹性模量。
假设压电叠堆中压电陶瓷片数量为n,根据应变关系,推导出压电叠堆的总变形量为
δp=nlpεp
(4)
图3是夹持机构位移计算图,其中A点为压电叠堆输出点,B点为柔性铰链杠杆支点,C点为夹持臂的弯折点,D点为夹持臂与被夹持物体的接触点,AB段、BC段、CD段的长度分别为l1、l2和l3,夹持臂在点C处的弯折角度为θ。
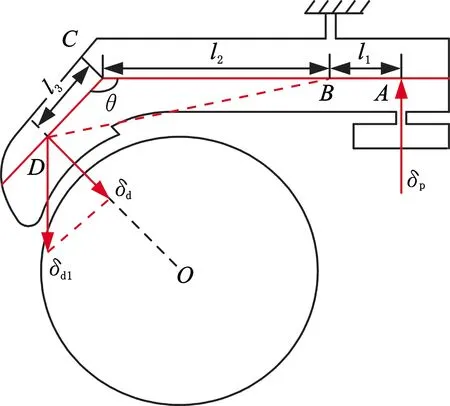
图3 夹持机构位移计算图
在压电叠堆变形量作用下,夹持臂沿柔性铰链为支点的转角为
α=arctan(δp/l1)
(5)
BD段的直线长度为
(6)
夹持臂末端与BD垂直方向的位移为
δd1=2lBDsin(α/2)
(7)
因此夹持臂末端沿被夹持物体径向的位移为
δd=δd1cos(π-α-θ)
(8)
夹持机构中柔性铰链切口半径和最小厚度分别为ro和co,则柔性铰链处的转动刚度[15]为

(9)
式中,lB、E分别为夹持机构的截面宽度和弹性模量。
柔性铰链处弯曲变形产生的弯矩为
MB=Kαzα
(10)
图4为夹持机构受力计算图,夹持机构受到三个力的作用,分别是压电叠堆的输出力Fp、柔性铰链的弯矩MB以及来自被夹持物体的力Fd。
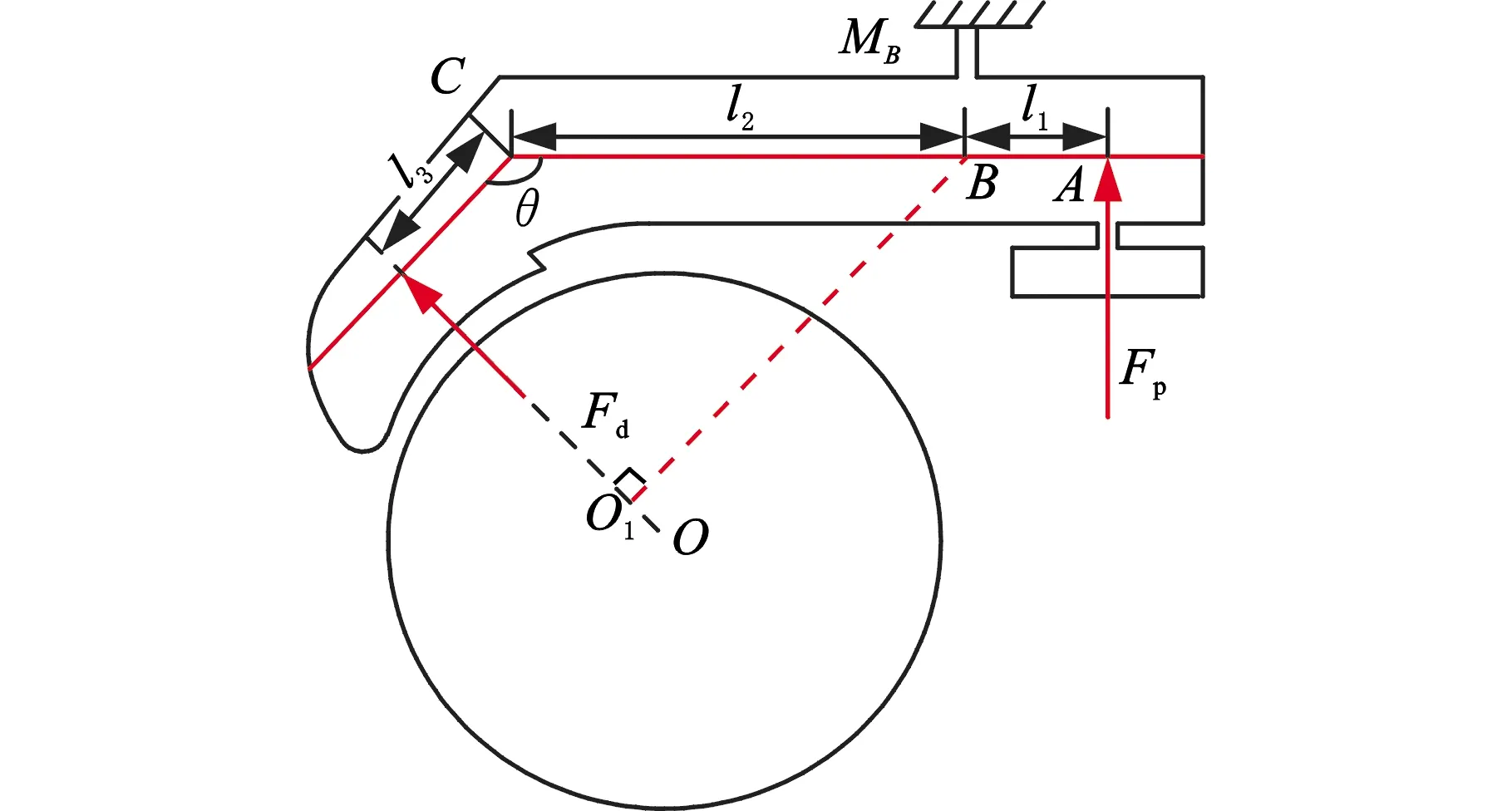
图4 夹持机构受力计算图
力Fd对B点之矩的力臂O1B长度为
lO1B=l2sin(θ-π/2)+l3
(11)
对夹持机构所有受力以B点取矩,建立平衡方程如下:
FdlO1B+MB-Fpl1=0
(12)
则来自被夹持物体的力为
(13)
夹持臂通过摩擦力来实现对被夹持物的夹持,夹持臂与被夹持物体之间的摩擦力为
Ff=μFd
(14)
式中,μ为摩擦因数。
3 数值仿真与实验
3.1 输出位移和力仿真
压电精密夹持机构采用两个5 mm×5 mm×30 mm的压电叠堆驱动,对式(8)和式(14)进行MATLAB数值仿真,可得到夹持臂末端沿被夹持物体的径向位移和夹持臂与被夹持物体之间的摩擦力,如图5所示。为了研究夹持臂运动范围,这里只考虑夹持机构在压电驱动下的自由变形,因此,夹持臂的径向位移处于非夹持状态。
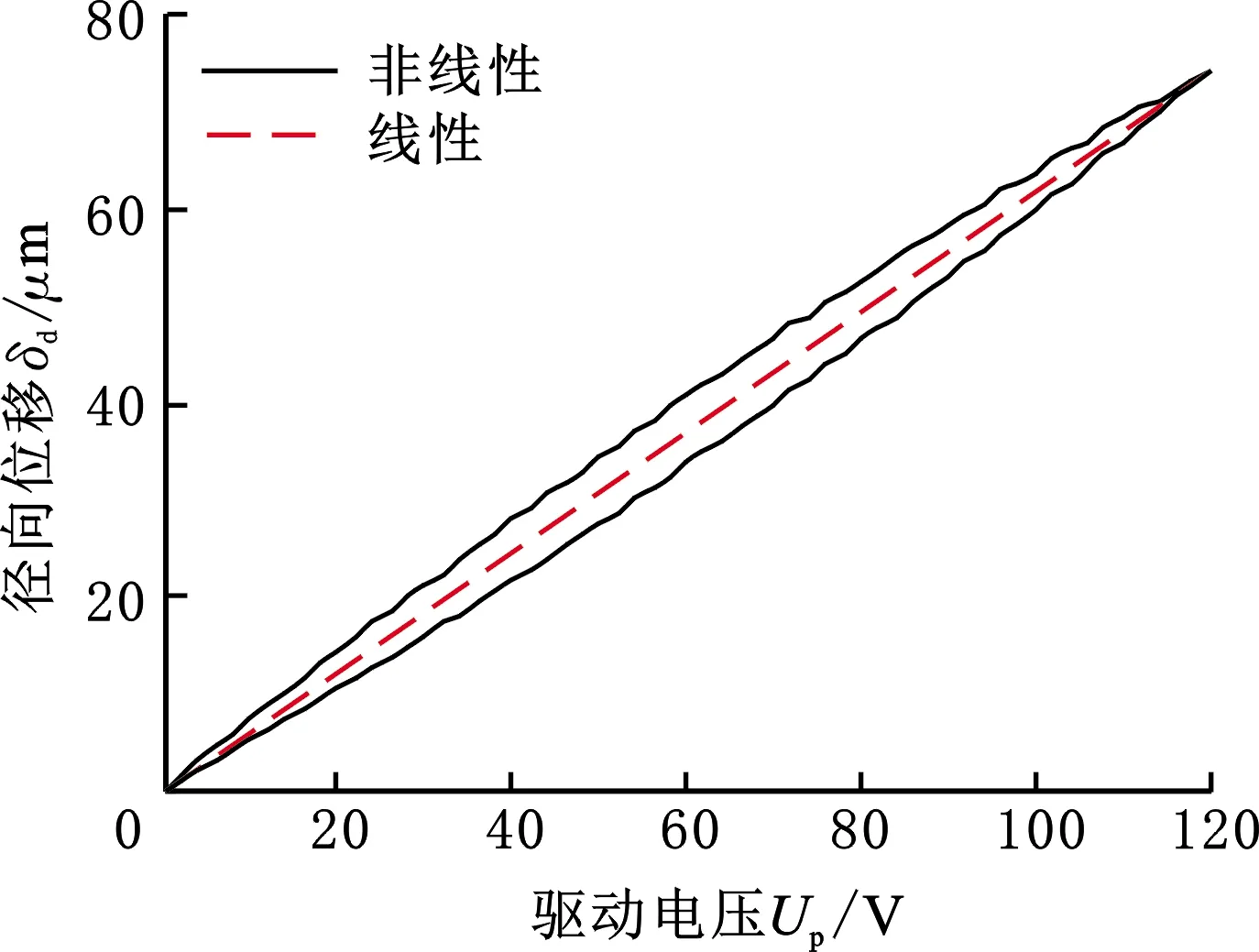
(a)夹持臂末端径向位移
由图5可知:①随着驱动电压的增大,夹持臂末端沿被夹持物体的径向位移非线性增大,且出现迟滞现象,位移上升曲线和位移下降曲线不重合,最大迟滞误差为17.1%;②在驱动电压120 V时,在未被夹持状态下夹持臂末端沿被夹持物体的最大径向位移为74.2 μm;③夹持臂与被夹持物体之间的摩擦力随驱动电压的增大而非线性增大,仍然存在迟滞现象,最大迟滞误差为17.1%,与位移迟滞误差一致;④在驱动电压120 V时,夹持臂与被夹持物体之间的最大摩擦力为7.1 N。
为了研究压电精密夹持机构综合性能的影响因素,分析了参数对夹持臂输出位移的影响,结果如图6所示。由图6可知:①随着参数的变化,夹持臂末端径向位移曲线的变化趋势不变,均是关于驱动电压Up出现迟滞变化,不同点在于,当电压一定时,不同参数对应的位移所有差别;②夹持臂末端径向位移随参数d33、l2、l3和θ成正比例增大,且驱动电压越大时,位移增加的幅度越大;③夹持臂末端径向位移随参数lp和l1的变化趋势与随d33、l2、l3和θ的变化趋势相反,当lp和l1增大时,夹持臂末端径向位移减小,且lp的变化对位移的影响更大。
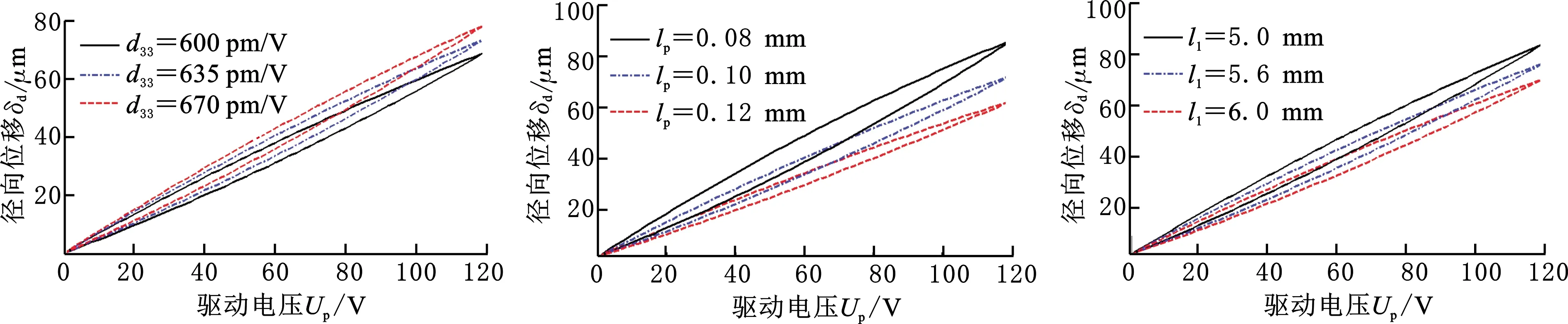
(a)d33的影响 (b)lp的影响 (c)t1的影响
同时,研究在120 V电压驱动下参数对夹持臂夹持力的影响,结果如图7所示。由图7可知:①随着参数d33、Sp和l1的增大,夹持臂摩擦夹持力近似线性增大;②夹持臂末端摩擦夹持力随lp、l2、l3和θ的增大而非线性减小,且随lp的变化幅度最大,非线性程度最高;③由参数变化对夹持力的敏感性可知,lp变化对夹持力的影响最大,θ变化对夹持力的影响最小。
综合图6和图7,d33和lp对夹持臂末端径向位移和夹持臂摩擦夹持力的影响规律相同,夹持臂输出位移和夹持力随d33正比例变化,而随lp非线性负比例变化;参数l1、l2、l3、θ对夹持臂输出位移和夹持力的影响规律相反。因此,参数l1、l2、l3和θ的选取对夹持机构综合性能的影响较大,应当根据夹持机构的适用范围选取参数值。
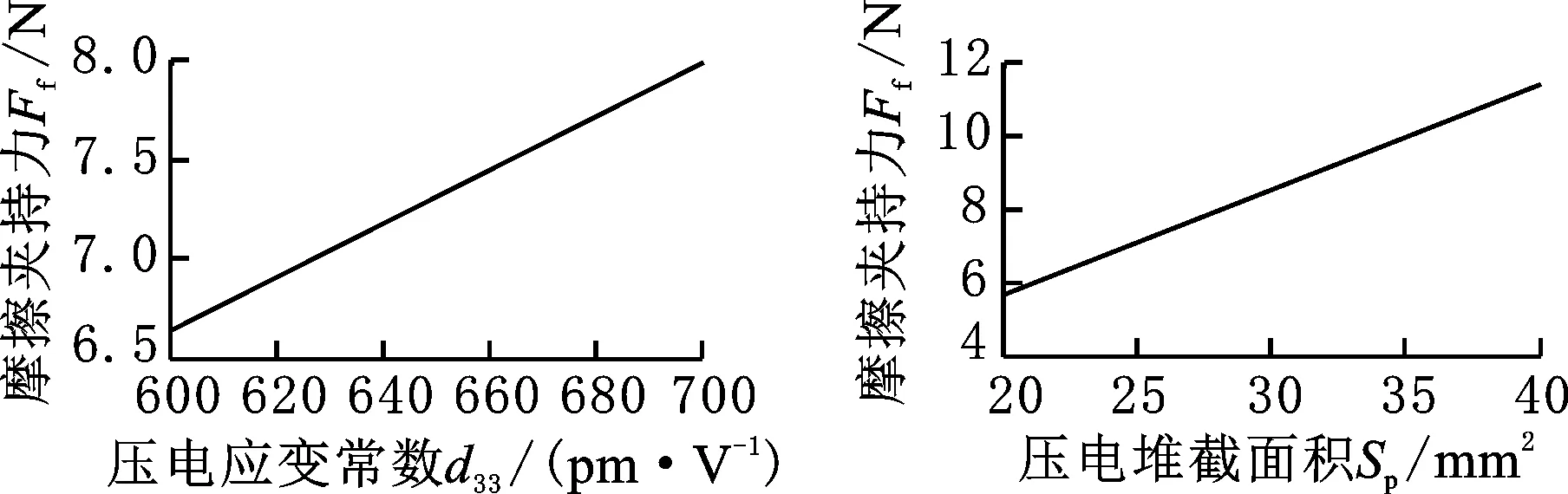
(a)d33的影响 (b)Sp的影响
3.2 实验测试
为了验证本文提出的压电精密夹持机构的综合输出性能,对它进行了实验测试。首先对夹持臂的径向输出位移进行测试,测试系统如图8所示。利用哈尔滨芯明天科技有限公司生产的三通道压电控制器对压电叠堆元件进行电压驱动,压电控制器由上位机软件进行控制。采用量程为0~1 mm的LVDT电感式微位移传感器对夹持臂的径向输出位移进行采集。微位移传感器采集的位移信号通过传感器控制器传递给电脑,通过上位机软件显示在电脑屏幕上。

(a)测试现场图
图9所示为两个夹持臂的输出位移测量值,图10所示为输出位移实验值与仿真值之间的误差。由图9和图10可知:①两个夹持臂的测试位移均存在迟滞效应,在驱动电压为120 V时,两夹持臂的最大径向位移分别为73.8 μm和68.6 μm;②两个夹持臂的输出位移随电压变化的实验曲线近似理论仿真曲线,驱动电压越大,实验值与仿真值越接近。当驱动电压大于50 V时,误差在10%以内。
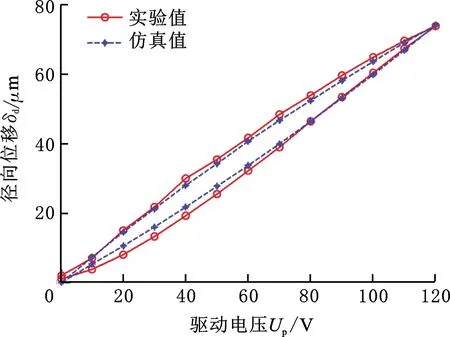
(a)夹持臂一
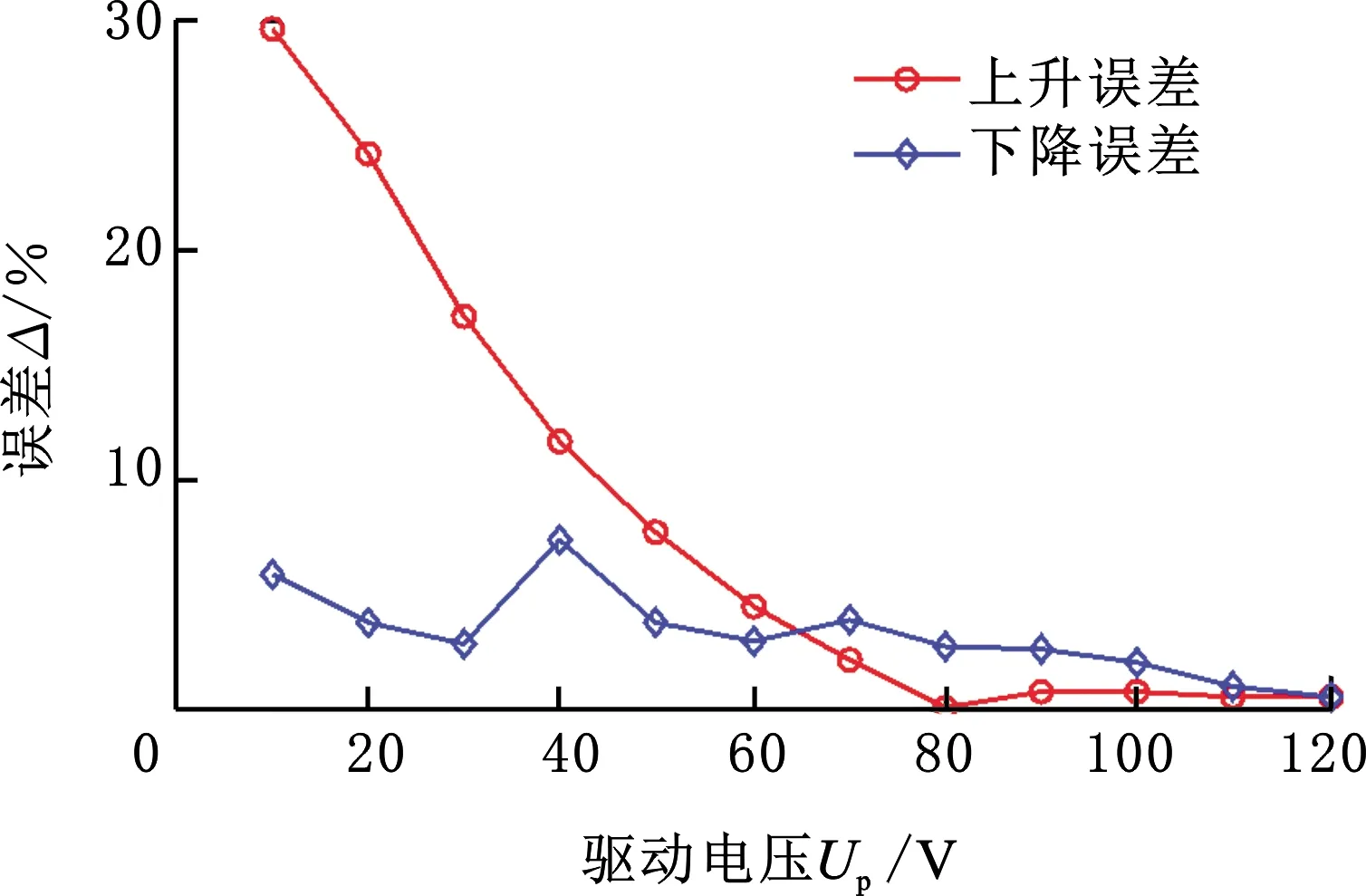
(a)夹持臂一
通过两夹持臂输出位移测试结果可知,两夹持臂输出位移不一致,而按照理论设计,两个夹持臂的径向输出位移则应相同,造成测试结果偏差的主要原因有以下几方面:①加工制造误差造成两夹持臂不对称,虽然本文中采用的夹持机构实验样机通过慢走丝线切割加工完成,但是对精密零件来说,微小的误差可能造成输出结果的不一致,这里面柔性铰链的加工误差对夹持臂输出位移影响最大;②实验中采用的两个压电叠堆虽然采用同一厂家同一批次的压电叠堆,但通过测试发现在相同驱动电压下两压电叠堆的输出位移之间存在一定误差;③初始预紧力偏差造成的位移输出不对称,作者在对压电叠堆进行预紧时,调整了两夹持臂的预紧力使其尽量相等,但是误差仍然不可避免,初始预紧力会造成两个压电叠堆输出位移不一致;④传感器测试误差造成两夹持臂输出位移不对称,本文采用LVDT电感式微位移传感器对夹持臂进行输出位移测试,而在测试中由于传感器触头与两夹持臂之间的初始预紧力不同,会造成一定范围内的测试误差。
利用“艾德堡”拉压力测力计对夹持臂的摩擦夹持力进行实验测试,测试系统如图11所示。夹持臂与被夹持物体之间的摩擦夹持力分为切向摩擦力和轴向摩擦力。对于两个已知零件,其压力和摩擦因数是确定的,因此,两个零件之间的理论摩擦力是确定的。这里通过实验方式分别测试夹持臂与被夹持物体之间的切向摩擦力和轴向摩擦力。本文中被夹持物的材料采用普通45钢,夹持臂由铝合金材料通过慢走丝线切割加工制造,通过查询机械设计手册以及综合考虑制造精度等因素,取摩擦因数为0.1。夹持臂与被夹持物体间的压力与驱动电压有关,驱动电压一定时,压力是恒定值,随着驱动电压的增大,压力值增大。夹持臂与被夹持物体间的压力如表1所示。

图11 夹持臂输出切向摩擦力实验系统
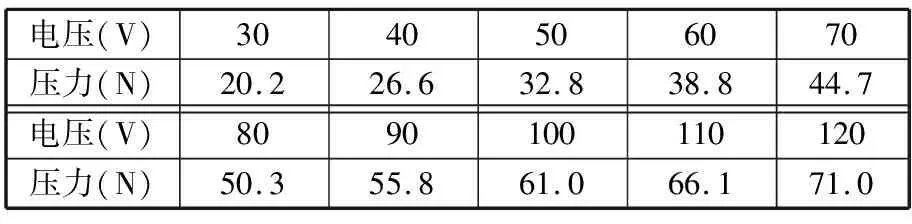
表1 夹持臂与被夹持物体间的压力
切向摩擦力主要是夹持臂和被夹持物沿圆周切向的摩擦力,其测试原理如图12所示。切向摩擦力测试步骤如下:①在被夹持物沿圆周方向缠绕测力绳,测力绳起点通过螺钉固定在螺纹孔处;②测力绳末端固定于测力计挂钩处;③从电压为30 V开始加载测试,每增加10 V加载测试一次,初始时刻被夹持物体和夹持臂处于临界接触;④在恒定电压下,缓慢拉动测力计末端,可以看到测力计读数增大,当测力计读数增大到一定程度时,被夹持物体发生一定角度偏转,此时测力计临界读数即为瞬时最大切向摩擦力,恒定电压下连续测试N次,再取平均值即为此恒定电压下的最大切向摩擦力,其表达式为
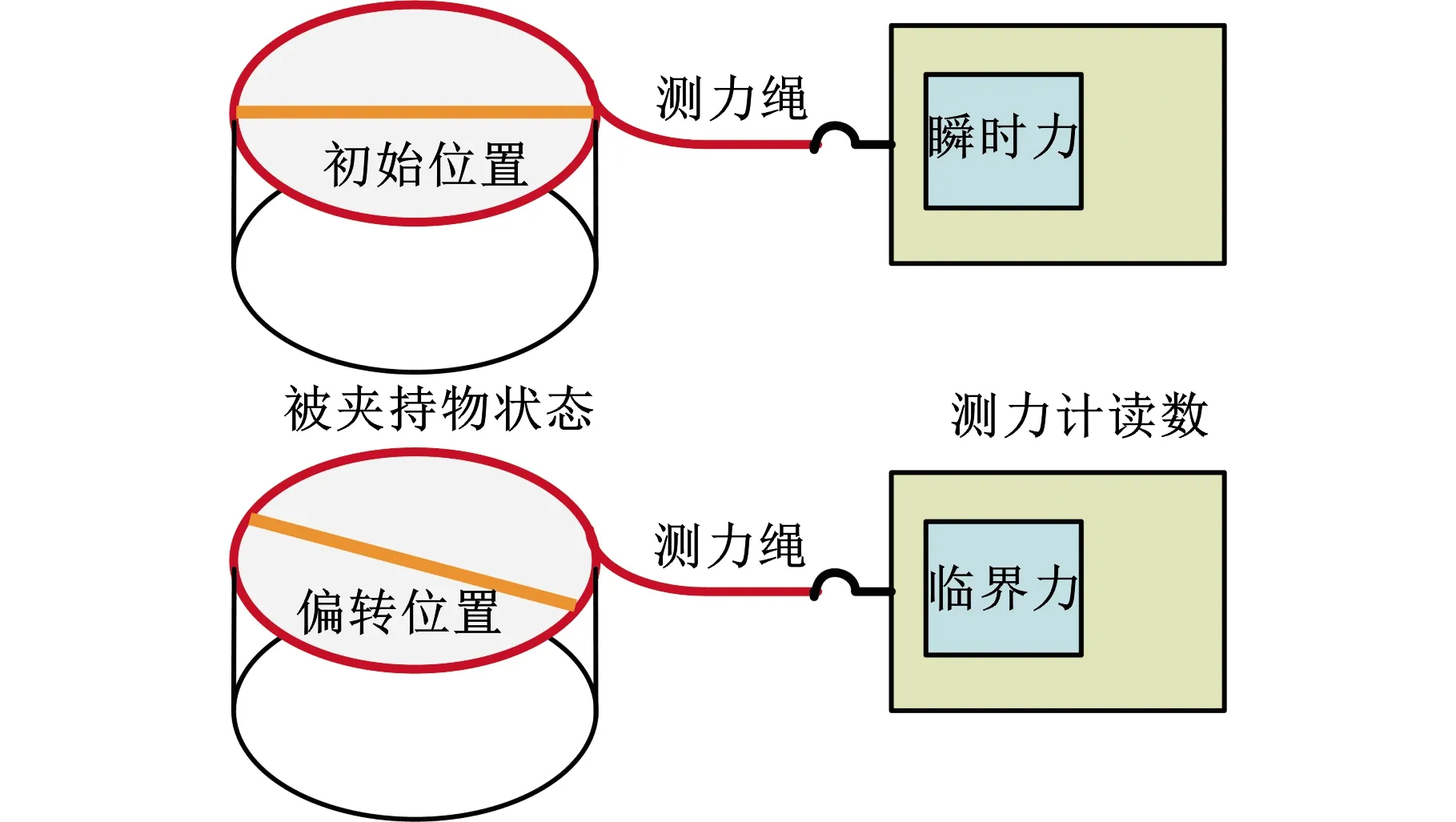
图12 切向摩擦力测试原理
(15)
⑤完成一定电压下的切向摩擦力测试之后,继续增加驱动电压10 V,直到120 V下摩擦力测试完成后结束实验。
轴向摩擦力主要是沿被夹持物体轴向的摩擦力,其测试原理与切向摩擦力类似,如图13所示。轴向摩擦力测试步骤如下:①将测力计安装在可调支架上,支架下端通过磁座的磁力吸附在工作台上;②被夹持物上端通过预留的螺纹孔安装辅助测试装置,并将辅助装置上端与测力计连接;③与切向摩擦力测试类似,从驱动电压为30 V开始对夹持机构进行轴向摩擦力加载测试,每增加10 V加载测试一次,初始时刻被夹持物体和夹持臂处于临界接触;④利用可调支架上的微调机构调节测力计的高度,随着高度方向的位移增加,测力计读数缓慢增大,当测力计读数增加到一定程度时,被夹持物体沿高度方向发生一定范围的滑动,此时测力计临界读数即为瞬时最大轴向摩擦力,同理,在恒定电压下连续测试N次,对N次取平均值即为此恒定电压下的最大轴向摩擦力,其表达式为
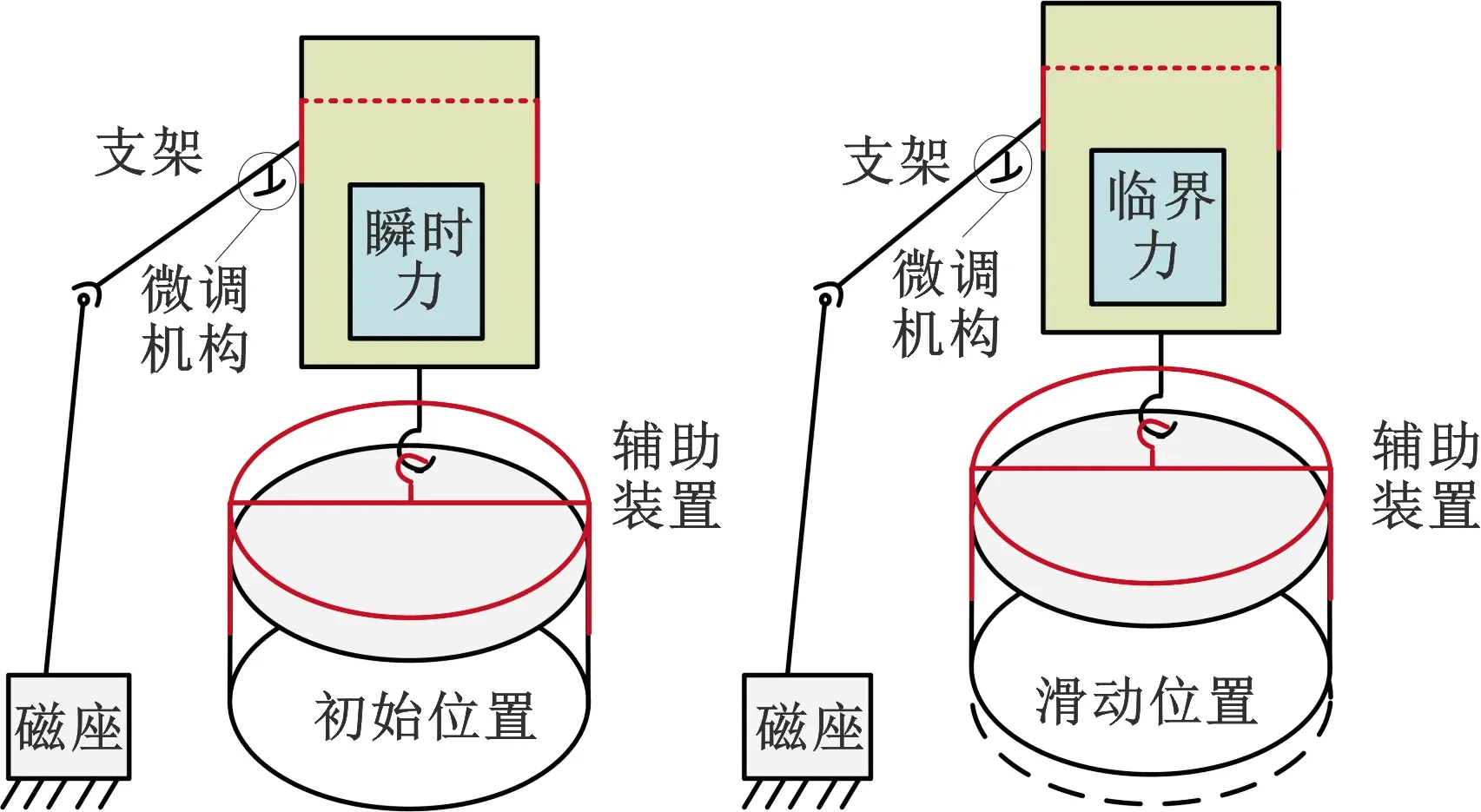
图13 轴向摩擦力测试原理
(16)
⑤完成一组测试后,改变驱动电压,进行下一个电压值下的轴向摩擦力测试,直至30~120 V范围内的所有测试完成。
摩擦力测试结果如图14所示。由图14可知:①随着驱动电压的增大,切向和轴向摩擦夹持力均增大。在120 V时,最大切向和轴向摩擦夹持力分别为7.8 N和5.7 N;②切向摩擦夹持力随电压变化实验曲线与仿真曲线更接近,误差远小于轴向摩擦夹持力误差。

(a)切向摩擦夹持力
总之,实验验证了压电夹持机构的输出性能以及理论模型的正确性。
4 结论
本文提出了一种基于压电驱动的微型精密夹持机构,分析了夹持机构的工作原理。根据压电材料的非线性输出应变关系,建立了夹持机构的输出位移和受力模型,分析了夹持机构的输出特性,搭建实验平台,通过实验验证了所设计的夹持机构的综合性能。结果表明:①参数l1、l2、l3和θ的选取对压电夹持机构输出性能的影响较大;②两个夹持臂的测试位移与仿真位移均存在迟滞效应,驱动电压为120 V时,两夹持臂的最大径向位移测试值分别为73.8 μm和68.6 μm;③当驱动电压大于50 V时,夹持臂输出位移测试值与仿真值之间的误差在10%以内;④在120 V时,最大切向摩擦夹持力和轴向摩擦夹持力的实验值分别为7.8 N和5.7 N。
