一种平面闭链腿式机构的尺度参数优化设计

王仙业 刘海涛 黄 田

天津大学机构理论与装备设计教育部重点实验室，天津，300354

0 引言

腿式机器人采用足端离散接触地面的方式跨越障碍，对非结构化环境具有很好的适应性，因此在空间探索、战场侦察、抗灾救援等方面具有良好的应用前景[1-3]。其中，基于平面多闭环连杆机构的腿式机器人具有控制简单、可靠性高等特点，引起了学术界的广泛关注[4-7]。在过去的几十年中，研究人员提出了众多闭链腿式机构[8-12]，如Chebyshev机构、Klann机构、Theo Jansen机构(TJL)等。

在此类机构中，TJL可以生成与步行哺乳动物相似的足端轨迹，且该轨迹底部平缓，可有效减小行进过程中由惯性力造成的杆件与地面间的冲击，保证了腿式机器人的平稳运动[13-14]。国内外学者围绕TJL开展了大量研究工作[15-18]。KOMODA等[19]利用虚功原理，推导了Chebyshev、Klann和TJL三种机构的动力学模型，并在曲柄尺寸、输入角速度和机构总质量相同的条件下，对比了三种机构的足端轨迹和能量消耗，结果表明TJL的足端轨迹底部最为平缓，且总能耗最低，更适用于腿式机器人。HAGHJOO等[20]以成年人在行走过程中踝关节相对于臀部生成的运动轨迹为目标，优化了TJL的尺度参数，据此设计了一款下肢康复训练设备。LIU等[21]以人在上楼梯时的步态作为目标轨迹，研究了TJL的优化设计问题，并基于优化结果设计了一种爬楼梯机器人，实现了该步态轨迹的模仿。文献[22-24]以输入能量最小为优化目标，综合了TJL的尺度参数。文献[25-26]通过调节机构的杆长和机架铰接位置，将TJL设计成一种变参数机构，从而获得可变化的末端输出运动。

鉴于TJL输出的足端轨迹底部平缓、适用于腿式机器人的平稳运动，本文以TJL的足端轨迹为优化目标，研究一种平面六杆闭链腿式机构[27]的尺度参数优化设计问题，使其能够很好地复现TJL输出的运动轨迹。

1 机构描述与运动学分析

1.1 机构描述

本文研究的平面闭链腿式机构如图1所示。该机构由6根连杆和7个转动关节组成，杆AD为机架，杆ABE为原动件，杆CFG为输出件，点G的运动轨迹为该机构的足端轨迹。利用Grübler-Kutzbach准则计算该机构的自由度:

图1 平面闭链腿式机构结构简图

(1)

式中，n、j、fi分别为杆件数目、转动关节数目、第i个转动关节的自由度,n=6，j=7，fi=1。

由式(1)可知，该机构的自由度为1，因此该机构在杆ABE的驱动下具有确定的末端输出运动。

1.2 运动学分析

如图1所示，在点A处建立坐标系Axy，水平方向为x轴。在该坐标系下，可将Ⅱ级杆组(杆EF-CFG)中点G的位置矢量表示为

rG=rC+q1(rF-rC)+q2M(rF-rC)

(2)

式中，lCF、lCG、lFG分别为杆CF、CG和FG的长度。

由式(2)可知，为得到rG，需要先计算rC和rF。类似地，可将Ⅱ级杆组(杆BC-CD)中点C的位置矢量表示为

rC=rB+q3(rD-rB)+q4M(rD-rB)

(3)

lBD=‖rD-rB‖rB=(lAcosα，lABsinα)T

rD=(lADcosθ0，lADsinθ0)T

式中，lA、lAD、lBC、lCD分别为杆AB、AD、BC和CD的长度；lBD为点B与点D之间的距离；α为曲柄的输入角；θ0为机架与x轴之间的固定安装角度。

在Ⅱ级杆组(杆EF-CFG)中，点F的位置矢量为

rF=rC+q5(rE-rC)+q6M(rE-rC)

(4)

lCE=‖rE-rC‖rE=(lAEcosβ,lAEsinβ)T

式中，lAE、lBE、lEF分别为杆AE、BE和EF的长度；lCE为点C与点E之间的距离；β为杆AE与x轴之间的夹角。

将式(3)和式(4)代入式(2)，可得点G的位置矢量:

rG=ArB+BrE+CrD

(5)

A=(1-q3-q5q1+q3q5q1)I+aM+

bM2+(q4q6q2)M3

B=q5q1I+(q6q1+q5q2)M+q6q2M2

C=(q3-q3q5q1)I+cM-dM2-(q4q6q2)M3

a=q3q6q1+q3q5q2+q4q5q1-q4-q6q1-q5q2

b=q3q6q2+q4q6q1+q4q5q2-q6q2

c=q4-q3q6q1-q3q5q2-q4q5q1

d=q3q6q2+q4q6q1+q4q5q2

表1给出了文献[27]中该机构的尺度参数，其中θ0=0°。根据式(5)，可得到不同输入角度下机构的位形,如图2所示。由图2可知，该平面闭链腿式机构能够近似模拟步行哺乳动物的腿部运动，但在该组尺度参数下，其轨迹底部的平缓性稍差,因此，有必要进一步研究该机构的尺度综合问题，以得到更优的末端输出运动轨迹。

表1 闭链腿式机构量纲一尺度参数

(a)α=0° (b)α=36° (c)α=72° (d)α=108°

2 尺度参数优化设计

文献[20]给出了TJL的量纲一尺度参数(表2)。在该机构中，机架与x轴之间的固定安装角θ0=11.6°(图3)。由图3可知，TJL可连接机架与足端的杆CD和杆CG(图中绿色部分)，足端轨迹可视为由杆CD和杆CG的运动确定。注意到，在所提出的腿式机构(图1)中存在与图3相同的连杆，故在保证两种机构尺度参数lCD、lCG和运动参数φ3、φ5相同的前提下，即可得到相同的输出运动。为减少设计变量，令两机构的杆长lCD、lCG分别相等。此外，注意到φ3由曲柄摇杆机构ABCD(图中红色部分)确定，故令两机构中lAB、lBC、lAD和安装角度θ0的取值分别相等，使得在给定相同输入角α时，两种机构的φ3亦相等。在上述前提下，当φ5对应相等时，两机构的足端位置相同。

表2 TJL量纲一尺度参数

图3 TJL结构简图

根据前文推导的运动学模型，可得所研究机构(图1)中φ5的解析表达式：

(6)

TJL中φ5的求解可参见文献[19]。为便于区分，下文将TJL的φ5记为φ′5，且其余角度亦采用相同定义方式。进一步，结合式(3)和式(5)可知，式(6)中包含lBE、lEF、lCF、lAE和lFG共5个独立参数，将它们定义为设计向量

x=(lBE，lEF，lCF，lAE，lFG)T

(7)

2.1 目标函数与约束条件

本文的优化目标为两机构中点G的轨迹偏差最小，基于上述分析可将其转化为两机构的φ5与φ′5的偏差最小，即

(8)

其中，N为一个运动周期内输入角的离散点数目。当η取最小值时，可认为两种机构的足端轨迹最为相近。

为了保证设计结果的可行性，依据机构尺度参数间的几何关系来确定优化问题的约束条件。

基于上述分析，将两机构尺度相同部分重合，得到的结果如图4所示。结合图2可知，在一个运动周期内，杆BE绕点B旋转一周,故以杆BC为机架、杆BE为曲柄、杆CF为摇杆、杆EF为连杆(图4)。根据该曲柄摇杆机构的曲柄存在条件，可得到lBE、lEF、lCF之间的约束关系：

图4 两种机构的结构对比

c1=lBE+lEF-lBC-lCF<0

(9)

c2=lBE-min(lEF,lBC,lCF)<0

(10)

因两机构的lAB、lBC、lCD和lAD取值相同，故在一个运动周期内两机构的φ2(杆AB和杆BC之间的夹角)相等，因此，φ1和φ4满足如下约束关系：

c3=φ1+φ4=2π-φ2

(11)

式中，φ1为曲柄摇杆机构BEFC中杆BC与杆BE之间的夹角；φ4为杆AB和杆BE之间的夹角。

结合式(3)可知，φ1和φ4中仅包含lBE和lAE两个独立参数，故利用式(11)可得到lBE与lAE之间的隐式约束关系。类似地，在一个运动周期内两机构的γ2(杆BC和杆CD之间的夹角)相等，则φ5和φ满足如下约束关系：

c4=φ5+φ=2π+γ2-γ1

(12)

式中，γ1为杆CG和杆CF之间的固定角度；φ为杆CF与杆BC之间的夹角。

结合式(3)～式(5)可知，式(12)中仅包含lCF和lFG两个独立参数，故利用式(12)可得到设计变量lCF与lFG之间的隐式约束关系。

最终，本文所研究的平面闭链腿式机构优化设计问题被定义为如下单目标优化问题：

(13)

2.2 优化设计

根据等式约束c3和c4，可将设计变量进一步缩减为lBE、lEF和lCF。若采用一般的优化算法[12]，则需给定三个设计变量的取值范围。考虑到三个设计变量与已知量lBC构成曲柄摇杆机构BEFC，且约束条件c1和c2源自该机构的曲柄存在条件，故可参考曲柄摇杆机构的优化设计方法确定三个设计变量，从而简化优化问题的求解。

为设计该曲柄摇杆机构，首先确定其摇杆的摆角范围。将φ视为摇杆CF的摆角，它与φ5之间满足约束c4。注意到该约束同样存在于TJL中，即

φ′5+φ′=2π+γ2-γ′1

(14)

其中，φ′为TJL中杆BC与杆CF′的夹角；γ′1为杆CG与杆CF′的夹角(图4)，因此，可参考TJL确定φ的摆角范围。图5所示为一个运动周期内TJL中φ′的变化曲线。由图5可知，φ′的两个极值分别为φ′max=181.68°和φ′min=103.96°，所对应的输入角分别为348.55°和167.94°，则摆角φ应满足

图5 TJL中φ′的变化曲线

Δφ=φmax-φmin=φ′max-φ′min=77.72°

(15)

其次，需要确定摇杆CF的极限位置。根据TJL中φ′的两个极值及其所对应的输入角，得到TJL的两个极限位置，如图6所示。为了保证φ5和φ′5具有相同的变化趋势，两机构应同时达到极限位置。由于两机构的四杆机构ABCD相同，故需要设计的曲柄摇杆机构BEFC的机架BC可由TJL的两个极限位置确定。进而，可确定φ的极值所对应摇杆的两个极限位置(C1F1和C2F2)，如图6所示。

(a)φ和φ′均为最大值

根据曲柄摇杆机构极限位置的几何条件，即曲柄与连杆共线，可构造如下约束方程：

(16)

式中，a1、a2分别为曲柄摇杆机构BEFC两个极限位置处点B到点F的距离。

式(16)中包含lBE、lEF、lCF和φmax四个参数。为求解式(16)，根据两机构同时达到极限位置的条件进一步可得

‖rE1‖=‖rE2‖

(17)

i=1，2

φm1=φmaxφm2=φmax-Δφ

式中，rBi、rCi、rEi分别为两极限位置处点B、点C和点E的位置矢量。

式(16)和式(17)提供了3个约束方程，包含4个参数。因此，当φmax给定时，便可得到lBE、lEF和lCF。进一步，根据式(8)即可定量评价两机构足端轨迹的近似程度。为了避免曲柄摇杆机构BEFC存在奇异位形，并保证其摆角范围，给定φmax的取值范围为78°<φmax<180°，取离散点个数N=200，绘制η随φmax的变化曲线，如图7所示。由图7可知，当φmax=168°时，η取得最小值，因此，可认为此时两机构的足端轨迹最为接近。将φmax代入式(16)、式(17)、式(11)和式(12)，即可得到优化后机构的量纲一尺度参数(表3)。

图7 η随φmax的变化曲线

表3 优化后闭链腿式机构的量纲一尺度参数

在表1和表3两组尺度参数下，腿式机构的φ5与TJL中φ′5的变化曲线见图8。由图8可知，优化后φ5的变化规律与φ′5更为接近。图9进一步对比了两组尺度参数下腿式机构与TJL的足端轨迹。优化后的机构与TJL具有相同的跨高h，且最大轨迹偏差小于0.26。上述结果表明，优化后闭链腿式机构可以很好地逼近TJL的足端轨迹。

(a)角度的变化曲线

(a)足端轨迹

3 多足移动机器人样机

利用优化后的尺度参数设计了一种多足移动机器人，其CAD模型如图10所示。整机包括左右布置的两个模块，每个模块包含一个主传动轴和两组前后布置的双足步行单元，每组双足步行单元由两个闭链腿式机构、传动齿轮组、传动同步带轮、曲柄轴组成。整机由安装在中间的两个电机驱动，并设置了电池仓来放置电池，通过同步带轮将动力传递给主传动轴；传动齿轮组分别与主传动轴和曲柄轴固连，主传动轴通过齿轮传动将动力分别传输到曲柄轴上；曲柄轴带动闭链腿式机构的曲柄转动，从而使闭链腿式机构输出足端运动，支撑机器人在地面移动。为减小机器人质量，机身框架由碳纤维板制成，其余构件采用光敏树脂材料3D打印成形。

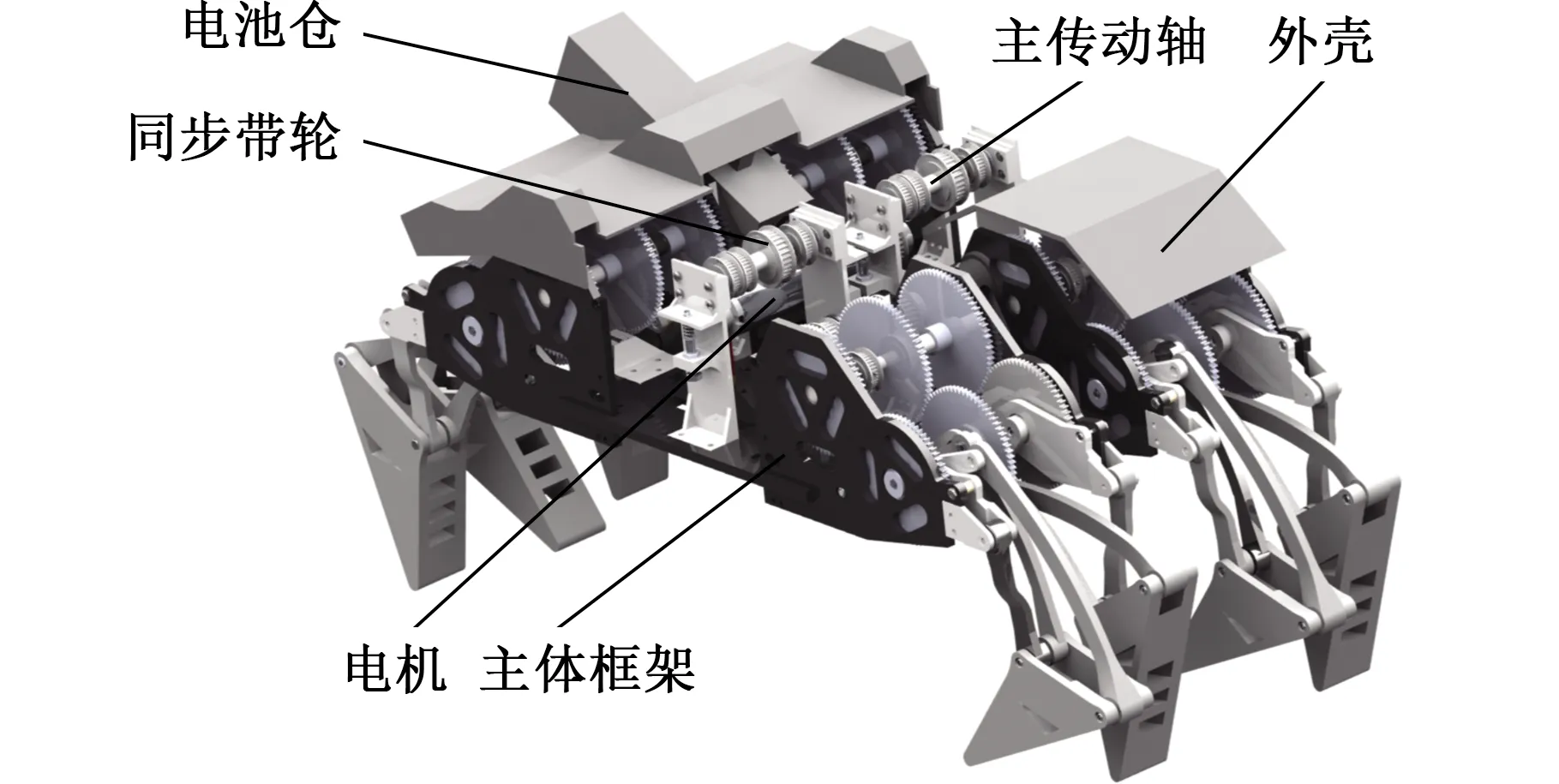
(a)整体结构

双足步行单元是机器人的行走装置，其行走步态直接反映机器人的运动状态。图11为该双足步行单元的结构示意图，由两个腿式机构组成，这两个腿式机构共用一个机架，共线布置的曲柄之间相位差为180°，通过单电机驱动实现两机构的同步运动。双足步行单元在水平地面行走时，交替完成支撑推进和迈步跨越的动作，从而使机架向前移动。如图11所示，支撑腿(红色)处于支撑阶段，足端支撑在点G处；摆动腿(蓝色)处于摆动阶段，足端在点G′处。当两腿式机构同时接触地面时，会有短暂的双重支撑阶段，即两足端分别处于点O1和点O2，两次双重支撑之间曲柄旋转180°，为一个行走周期。

图11 双足步行单元结构简图

为分析双足步行单元的运动平稳性，在足端支撑的G点处建立参考坐标系Gx′y′，水平方向为x′轴；在A点处建立连体坐标系Axy，在任意瞬时位形下坐标系Axy平行于坐标系Gx′y′(图11)。则在坐标系Gx′y′中，D点的位置矢量rGD可表示为

rGD=rD-2rG

(18)

据此，可得到双足步行单元机架在行走过程中的运动轨迹(假设无滑动)。类似地，亦可得到采用相同结构设计的TJL双足步行单元机架运动轨迹，如图12所示。通过对比可知，本文设计的双足步行单元在一个行走周期中机架上下波动幅度较小，能够有效保证机架的运动平稳性。

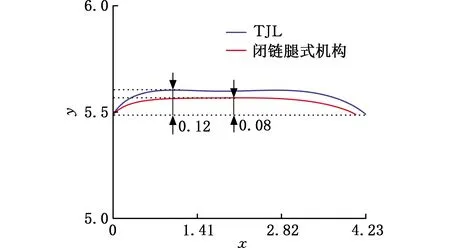
图12 行走时机架上固定点的轨迹

根据设计的多足移动机器人CAD模型，完成对电机、轴承、控制器等零件的选型，制作、装配，得到如图13所示的多足移动机器人实物样机，包含机器人本体、驱动控制系统以及电池。该样机的主要参数见表4。利用搭建的多足移动机器人开展行走实验(图14)，给定电机转速为30 r/min，机器人沿直线行进，速度可达0.06 m/s。利用激光测距仪得到样机在行走过程中主体框架与地面的距离,变化范围为140～142.2 mm，上下波动幅度小，证明了移动的平稳性。

图13 多足移动机器人实物样机

表4 样机参数

t=0 t=0.5 s t=1.0 s

4 结论

(1)在利用基本杆组法建立机构运动学模型的基础上，以该机构与TJL的足端轨迹偏差最小为优化目标，建立了考虑尺度参数间几何约束的单目标优化模型。通过考察机构的结构特点，利用曲柄摇杆机构的极限位置条件，有效减少了设计变量数目，并将优化设计问题简化为一维搜索问题，进而得到优化后的机构尺度参数。优化结果表明，最大轨迹偏差小于0.26，机构可近似复现TJL的足端运动轨迹。

(2)利用优化后的机构尺度参数设计了一种多足移动机器人，并分析了双足步行单元在一个行走周期内的运动平稳性。仿真与实验结果表明，该双足步行单元能够有效保证多足移动机器人的运动平稳性，从而验证了设计方案的可行性。