改进的正弦辅助多元经验模式分解及其在滚动轴承故障诊断中的应用

吴利锋 吕 勇 袁 锐 朱 熹 游 俊

1.武汉科技大学冶金装备及其控制教育部重点试验室，武汉,4300812.武汉科技大学机械传动与制造工程湖北省重点试验室，武汉,430081

0 引言

轴承通常在恶劣的环境下工作，容易出现故障[1]。一旦轴承发生损坏，如果没有及时发现并维修，会造成重大经济损失，因此及时对轴承关键的故障信息进行分析处理，确定故障发生位置对避免出现后续损失具有重要意义[2]。

常用的信号处理方法有小波变换(wavelet transform，WT)、局部均值分解(local mean decomposition，LMD)和变分模态分解(variational mode decomposition，VMD)。小波变换通常被用于处理机械故障信号，然而其处理效果取决于母小波选择是否正确，所以具有不自适应性的局限性[3]。局部均值分解能自适应地分解非平稳、非线性信号，但模式混合现象比较严重[4]。变分模态分解方法的模式混合现象较轻，但分量数目需要人为确定[5]。

经验模式分解(empirical mode decomposition，EMD)算法常被用于处理非平稳、非线性信号[6]。EMD算法存在端点效应、模式混合和不能处理多通道信号的缺点。为了克服EMD算法端点效应的缺点，时培明等[7]根据边缘局部极值点的特征进行延拓，对延拓的极值点序列进行包络拟合，估计出均值曲线。为了克服EMD算法模式混合的缺点，田海雷等[8]提出集成经验模式分解(ensemble empirical mode decomposition，EEMD)算法，将噪声添加到信号中作为辅助信号，并使用EMD算法处理集成信号，有助于引入额外的极值作为一个尺度来提取频率，减少模式混合的现象。互补集成经验模式分解(complete ensemble empirical mode decomposition，CEEMD)是EEMD的改进方法，通过在信号中成对地添加正负噪声辅助信号来减少残余分量[9]。自适应互补集成经验模式分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)算法通过使用EMD对噪声进行分解，产生多个频率范围的噪声分量，每分解一次信号分量就加入对应阶次的噪声分量，不仅减少了模式混合现象而且减少了噪声的残余[10]。为了克服EMD算法不适用于多通道信号处理的缺点，REHMAN等[11]提出多元经验模式分解(multivariate empirical mode decomposition，MEMD)算法，通过沿n维空间中不同方向的信号投影来计算多元信号的包络和局部均值，从而生成多个n维包络[12]。MEMD算法能够同时处理多通道信号，具有模式对齐的优点，然而无法避免EMD算法模式混合的缺点。为了克服MEMD算法模式混合的缺点，噪声辅助的多元经验模式分解(noise-assisted multivariate empirical mode decomposition，NA-MEMD)算法在额外的通道中添加了白噪声信号作为辅助信号，然后用MEMD算法进行处理[13]。NA-MEMD算法分解出来的本征模式函数(IMF)能够根据准二元滤波器组结构进行对齐，有助于缓解IMF之间的模式混合现象，但会导致噪声泄漏到原始信号通道，从而对分解结果产生干扰[14]。为了克服MEMD算法的模式混合现象，减少NA-MEMD算法噪声泄漏的问题，GE等[15]提出正弦辅助多元经验模式分解(sinusoidal assisted multivariate empirical mode decomposition，SA-MEMD)算法，通过在额外的通道中添加独立的正弦辅助信号减少了模式混合现象和噪声泄漏的干扰，相关研究证明，SA-MEMD算法在脑电信号的处理中能够缓解模式混合问题。

针对轴承故障中存在较大的噪声，干扰SA-MEMD分解性能的问题，提出使用非局部均值降噪理论进行预处理。在SA-MEMD算法中辅助信号的构造是算法的关键，而SA-MEMD的辅助信号需要凭经验去确定，增加了算法分解性能的不确定性。本文提出了一种改进的正弦辅助多元经验模式分解(improved sinusoidal assisted multivariate empirical mode decomposition，ISA-MEMD)算法，并分别用模拟信号和实际信号验证，ISA-MEMD比MEMD、SA-MEMD和NA-MEMD具有更好的分解性能。

1 非局部均值降噪理论

非局部均值(non-local means，NL-Means)是一种图像降噪算法，LAD等[16]通过加权图像邻域的相似度提出NL-Means算法，该算法广泛应用于图像的降噪处理。针对图像中存在的冗余信息，该算法通过设定两个固定大小的窗口即搜索窗口和邻域窗口来计算所有像素点的相似程度，然后通过加权所有相似的分量来消除噪声，达到降噪效果。由于机械故障信号中存在大量相似成分，其噪声具有随机性的特点，因此受图像降噪的启发，LYU等[17]将NL-Means算法应用于机械设备轴承信号降噪。将NL-Means算法应用于故障信号的主要作用是去除混在信号中具有随机性的成分。在原始信号中添加噪声，则模拟信号可表示为

y(i)=x(i)+w

(1)

式中，y为观察到的信号；x为原始信号；w为高斯白噪声。

在非局部均值滤波中，xe是x的估计值，为所有相似成分的加权平均值。NL-Means算法的过程表示为

(2)

(3)

Δ∈[s-P,s+P]LΔ∈[t-P,t+P]

式中，Z(t)为标准化常数，代表围绕中心s的所有相似模块权重的总和；v(s,t)为相似模块之间的相似度；λ为过滤参数，代表分别围绕s和t的相似成分；d2(s,t)为以s和t为中心的两个相似分量之间逐点差的平方；M(s)为搜索窗区域；P为比较块大小。

2 改进的正弦辅助多元经验模式分解基本理论

2.1 短时傅里叶变换

GABOR于1946年提出短时傅里叶变换(short-time Fourier transform，STFT)，其实质是加窗的傅里叶变换。在STFT过程中，首先将信号乘以一个时间有限的窗函数h(t)，再对其进行傅里叶变换，并假设这个非平稳信号在分析窗的短时间间隔内是平稳的，通过窗函数h(t)在时间轴上的移动，对信号进行逐段分析得到信号的一组局部“频谱”[18]。短时傅里叶变换定义为

(4)

式中，h(τ-t)表示分析窗函数。

由式(4)可知，信号u(t)在时间t处的短时傅里叶变换就是信号乘以一个以t为中心的分析窗h(τ-t)，再对其作傅里叶变换。u(t)乘以分析窗函数h(τ-t)相当于取出信号在分析时间点t附近的一个切片。对于给定时间t，STFT(t,f)可以看作该时刻的频谱。当窗函数取h(t)≡1时，短时傅里叶变换相当于传统的傅里叶变换。时频分析中，窗函数的宽度要根据信号特点进行调整，才能得到最优的局部化性能。

2.2 多元经验模式分解

REHMAN等[11]提出多元经验模式分解算法，该算法将n个变量信号(n>2)视为N维时间序列，并在N维空间中选择合适的方向向量。n个变量信号分别根据选定的方向向量来形成投影信号并计算每个投影信号的所有包络，然后取这些信号的平均值得到多元信号的局部均值，最后按照标准EMD计算步骤得到所有IMF组。从而实现MEMD算法对多通道信号的分解。

N维空间的方向向量集可以视为n-1维球体的点集，从而将计算N维空间的方向向量集问题转换为计算均匀度的问题[19]。

目前存在两种方法能在MEMD算法中实现统一采样点集：①均匀角度采样法，该方法会导致球的两个极点处分布密度很高的采样点，不利于均匀投影；②使用准蒙特卡罗较低偏差序列(Hammersley序列和Halton序列[20])在n-1维球体上生成点集，该方法生成的方向向量更均匀。以Hammersley序列作为准蒙特卡罗下偏差序列对采样点集进行说明。对于满足

g=b0+b1d+b2d2+…+bKdK

(5)

bi∈[0,d-1]bi∈Zi=0,1,…,K

的任何非负整数g和质数d，函数φd由下式给出：

(6)

假设采样空间的维数为m，利用一组质数序列d1,d2,…,dm-1定义函数序列φd1(g),φd2(g),…,φdm-1(g)，则将m维的g个Hammersley点定义为

(g/r,φd1(g),φd2(g),φd3(g),…,φdm-1(g))

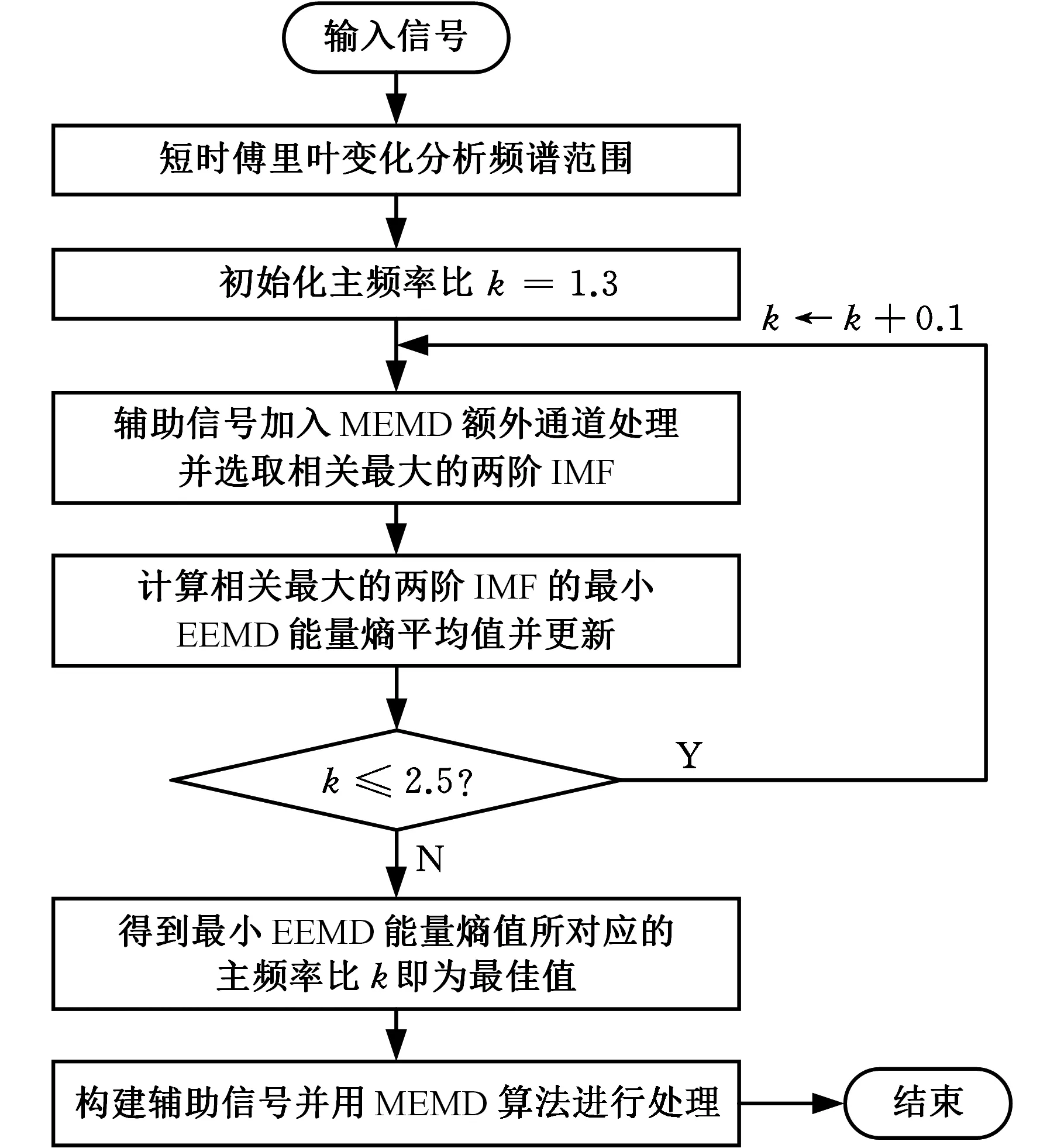
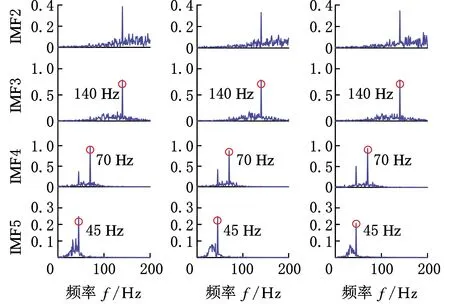
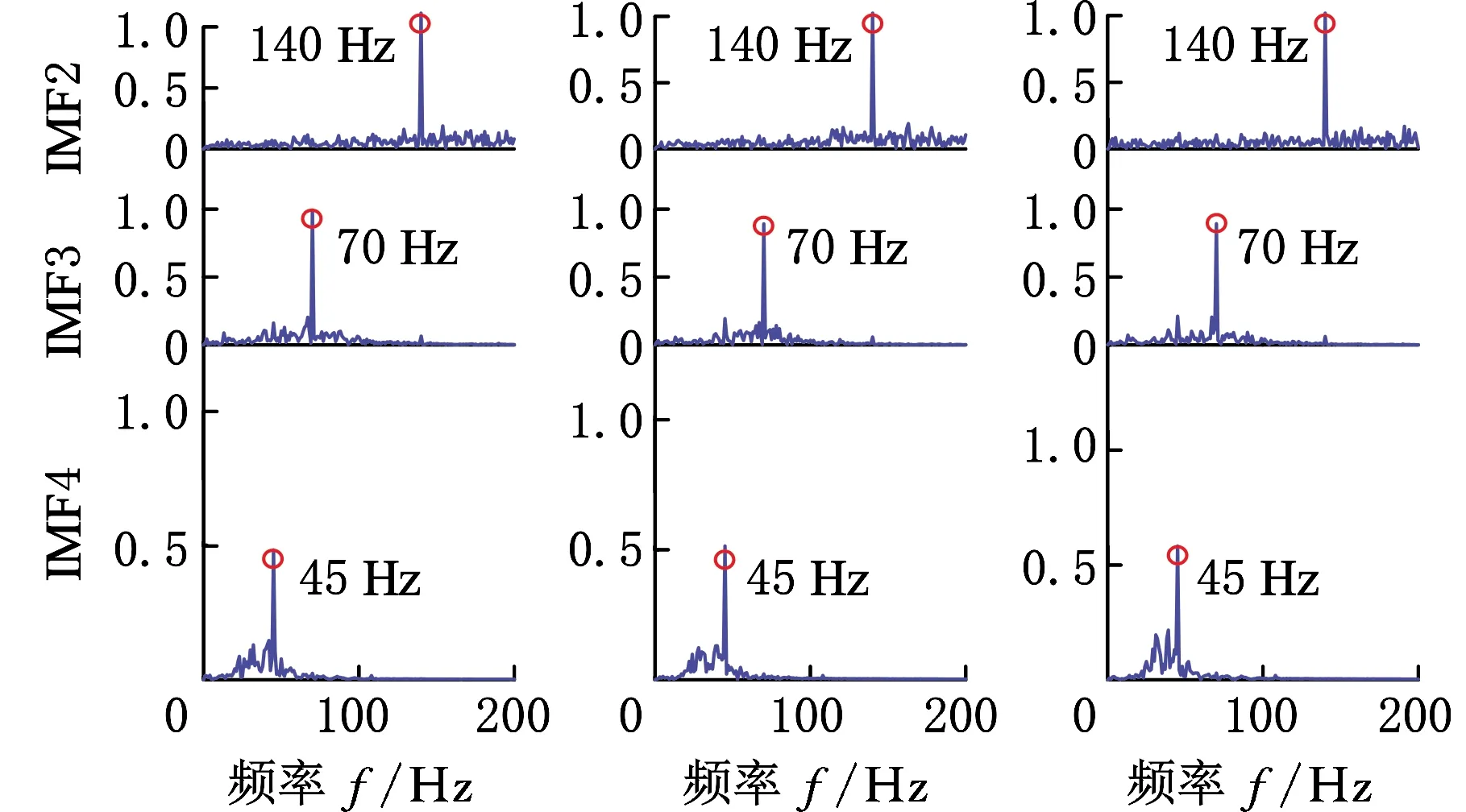
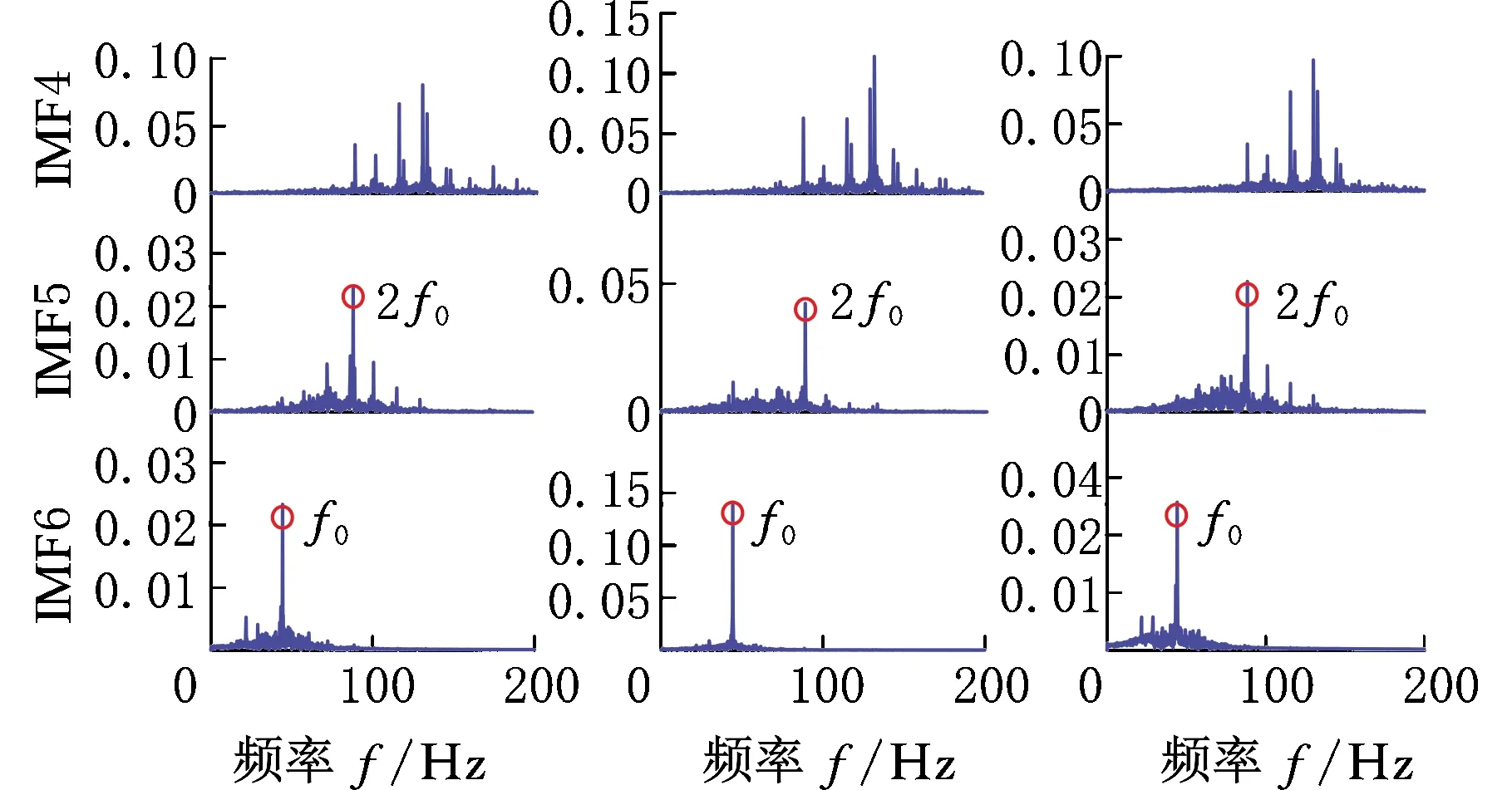
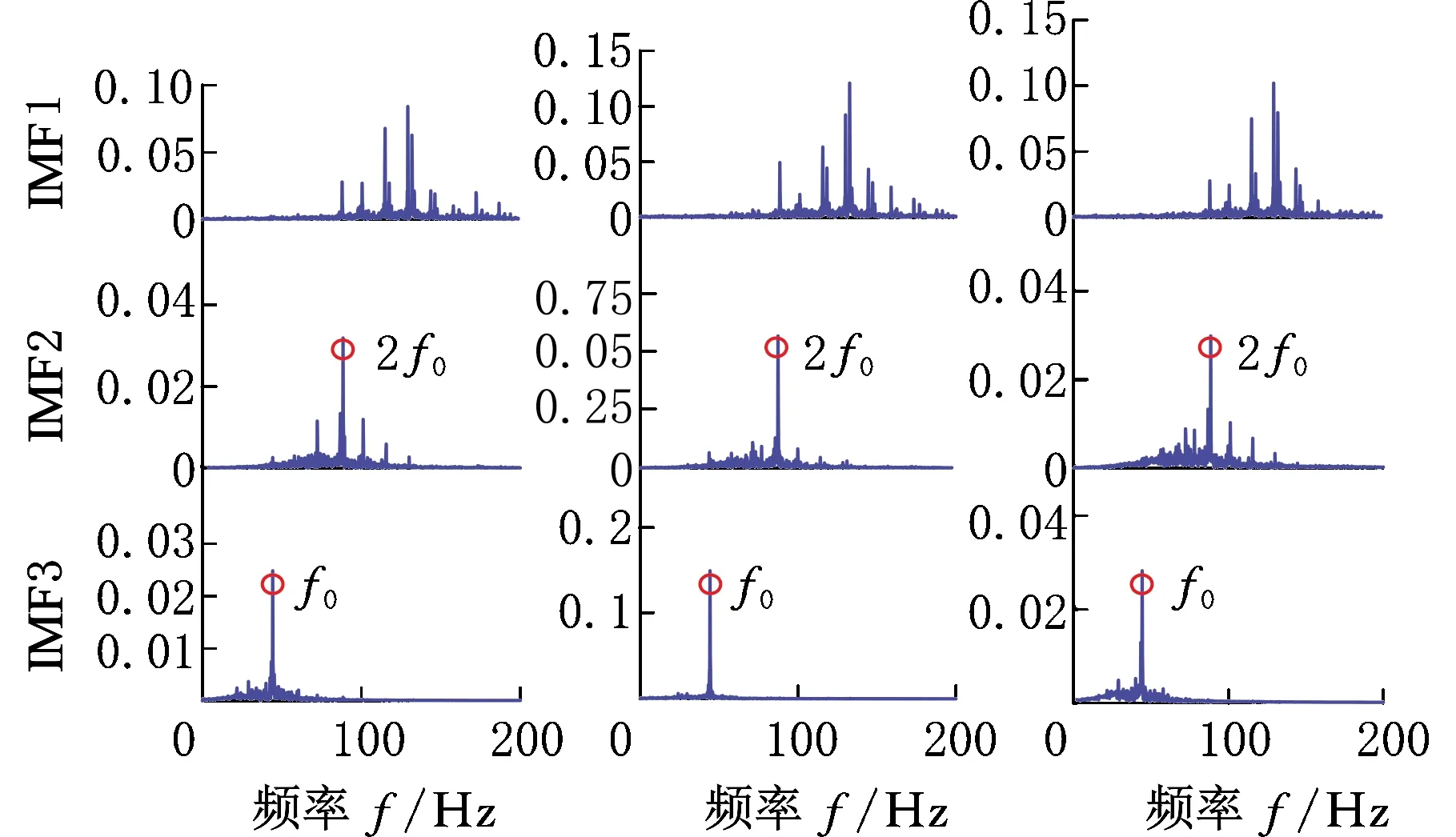
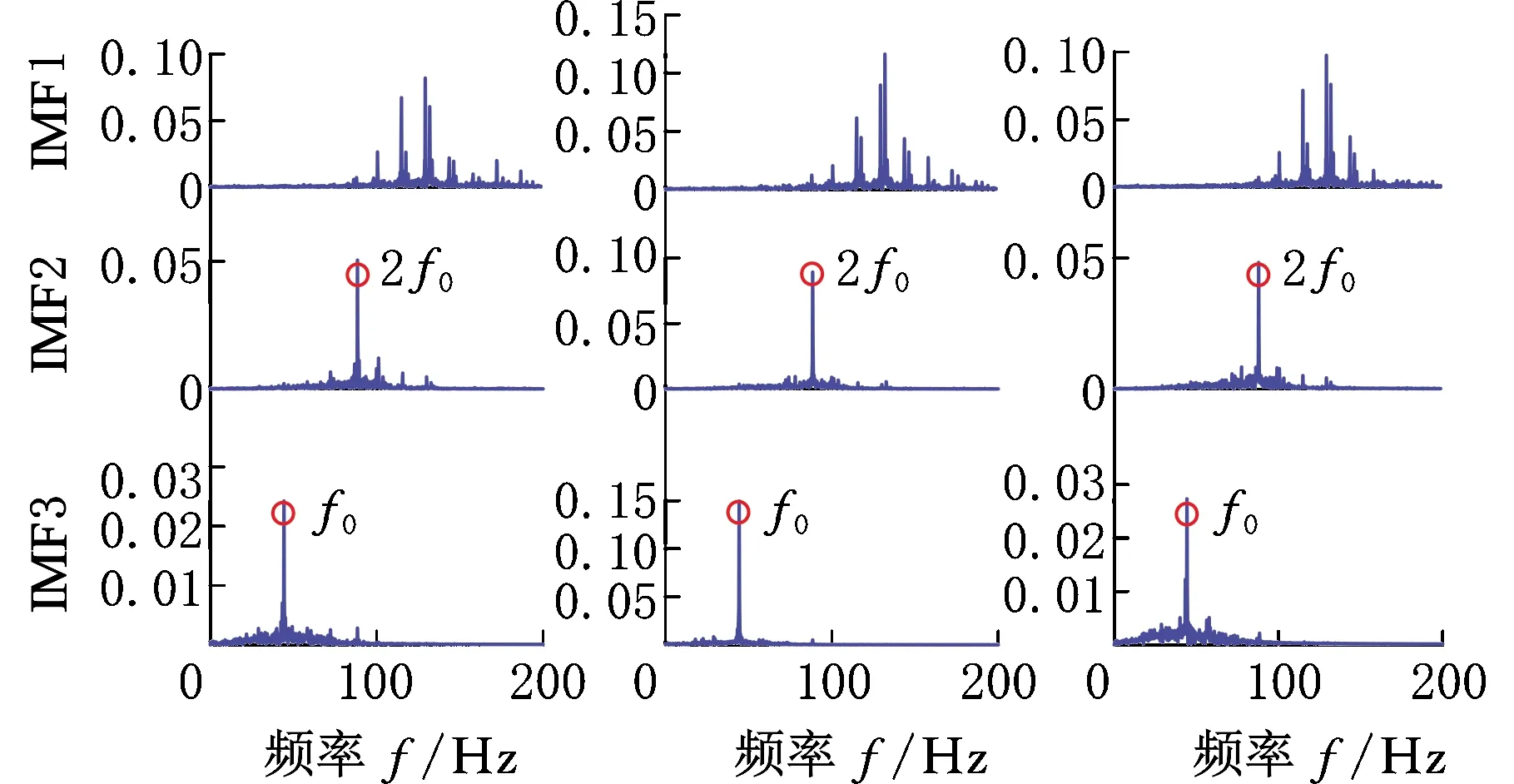
g=0,1,…,r-1d1

式中，r为Hammersley序列点的总数。

与EMD获得IMF的过程相同，MEMD是通过迭代来实现IMF的筛选，因此MEMD和EMD具有基本相同的筛选标准，即迭代停止标准。目前，迭代获得IMF有三种停止准则[21]:①由于应用了柯西型收敛条件，所以当相邻筛选结果之间的差异小于阈值时就停止迭代过程，典型阈值范围为0.2～0.3；②当两个连续的筛选过程N′次(N′由实际应用确定)具有相同数量的零交叉点和连续的极限点时，迭代将停止；③能量差跟踪方法确保不同IMF之间的能量差尽可能小，以便近似满足EMD的正交性。

2.3 正弦辅助多元经验模式分解

与NA-MEMD算法在额外通道中加入噪声辅助信号不同,在SA-MEMD算法中，通过加入规则的正弦分量来构造辅助信号，其形式如下：

(7)

式中，M为辅助信号中正弦波的数量；ai、fi分别为第i个正弦波的幅值和频率。

与NA-MEMD算法在额外通道中加入分布在整个频谱上的白噪声信号不同，SA-MEMD算法将辅助信号的频率范围与原始信号的频率范围设为大致相同，加入的辅助信号便不会带入超出原始信号频谱之外的其他频率。

(1)正弦分量频率的设定。NA-MEMD算法是通过准二元滤波器组结构对齐IMF来减少模式混合现象的[19]，同样，SA-MEMD算法也可以通过辅助信号中的每个正弦分量对齐IMF来减少模式混合现象。

(2)正弦分量振幅的设定。相关研究表明[16]，当振幅足够大时，正弦分量的相对振幅即a1,a2，…,aM在模式分解方面几乎没有差别，因此，将所有正弦分量的振幅设置为相同的值，即a1=a2…=aM。如果正弦分量的幅值太小，则每个正弦分量表示的模式的极值都不够大，会使原始信号的IMF没有用于对齐参考模式，从而导致MEMD无法筛选出这些模式，因此需将正弦信号的幅值设置得足够大。

SA-MEMD算法的步骤如下。

(1)创建正弦辅助信号。首先分析原始信号的频谱，当频谱的局部峰值相邻频率比大于1.3时，则将正弦分量设为等于频谱的局部峰值，反之，则尽可能使其靠近原始信号频谱的局部峰值；然后计算原始信号的平均幅值A，并将正弦辅助信号的幅值设置为A的10倍以上，当原始信号频谱中没有明显峰的频谱时，根据原始信号的频谱范围[flow,fhigh]和相邻分量频率比必须大于1.3的规则设定正弦分量。在满足最低和最高频率不超过[flow,fhigh]并且频率均匀分布在[flow,fhigh]条件的同时，设置尽可能多的正弦分量。

(2)将创建好的辅助信号添加到原始多元(Q通道)信号中，形成Q+1个通道多元信号。

(3)使用MEMD算法处理构造的Q+1个通道多元信号，从而获得多组IMF。

(4)从获得的Q+1个通道IMF中丢弃与正弦辅助信号相对应的通道，从而获得与原始信号对应的Q个通道IMF的集合。

2.4 EEMD能量熵

在正弦辅助多元经验模式分解算法步骤中,辅助信号的构造是算法的关键。主频率的比值决定了算法的分解性能。由于模式混合会使IMF分量能量分布更加发散，因此需要引入能量熵来评估模式混合的现象，从而确定合适的参数。模式混合现象越少，能量便越会集中在此频率带内，能量分布的不确定性越小，熵值越小[22]。因此能量熵越小，对应于这个辅助信号的分解性能越好。

获得由正弦辅助多元经验模式分解得到与原始信号相关的其中一个IMF分量，并用EEMD算法分解可以得到q个IMF，相应计算出各自的能量E1,E2,…,Eq。忽略残余分量，q个IMF的能量之和应该恒等于原始振动信号的总能量。由于各个IMF分量(c1,c2,…,cq)包含不同的频率成分，且具有不同的能量，从而形成了信号在频率域的能量分布[23]。EEMD能量熵的定义如下：

(8)

3 改进的正弦辅助经验模式分解

SA-MEMD算法起先应用于脑电信号处理。脑电信号是低频信号，噪声较小，而轴承故障信号是频率较高的信号，轴承运转时有较大的噪声。噪声太大会影响ISA-MEMD算法的分解性能，因此需先使用非局部均值理论对信号进行预处理。

由式(7)可以看出，辅助信号中正弦波的数量M、频率fi和幅值ai是算法的关键参数，这些参数的取值决定了ISA-MEMD算法分解性能。为了使ISA-MEMD算法表现出优异的分解性能，辅助信号关键参数的标准设定如下。

相关研究表明，如果多个不同频率的正弦分量组成的合成信号相邻频率比太小则会出现模式混合现象[24]。当相邻频率比大于阈值γ即fi+1/fi≥γ(fi+1>fi)时，EMD算法分解出来的IMF之间没有出现模式混合现象[25]。有资料表明，EMD算法的相邻频率比阈值γ一般是1.2 或1.4[24]，具体情况取决于所处理的数据集。

EMD算法相比MEMD算法的分解结果，模式混合现象更少，MEMD算法的频率分辨率优于EMD算法的频率分辨率。相关研究表明，MEMD算法相邻频率比大于1.3时有较少的模式混合现象[15]。为了使MEMD算法能够将信号完全分解为不同的频率分量，减少模式混合现象，ISA-MEMD算法将最小相邻频率比设为1.3。反复试验表明，如果主频率比大于2.5，将导致原始信号中的频率分量有较少的参考模式用于对齐，无法减少模式混合现象，因此将主频率比范围设为1.3～2.5。

首先获得原始信号频谱范围[flow,fhigh]，然后设置正弦信号的频率，确保设置的频率大于flow，小于fhigh。从SA-MEMD的算法步骤可以看出，分解性能取决于辅助信号主频率的取值范围。如果超出原始信号的频谱范围则会带入冗余分量，因此使用短时傅里叶变换对原始信号进行频谱分析，根据信号的频谱范围来构造辅助信号。SA-MEMD算法的主频率比决定了算法的分解性能，而原始的SA-MEMD算法只能根据经验来确定最佳主频率比，因此引入EEMD能量熵来选择分解性能最好的主频率比。一旦正弦信号的频率分布(fi)确定，正弦分量的数量M也随之确定。

根据相关研究[15]，正弦分量的幅值设定要大于原始信号的幅值，通常设置的幅值为原始信号平均幅值的10倍。一旦频率fi、频率个数M、辅助信号幅值ai确定，则辅助信号的构建完成。

ISA-MEMD算法流程如图1所示，具体步骤如下。

图1 ISA-MEMD流程图

(1)用短时傅里叶变换分析原始信号，设置辅助信号的频谱范围。

(2)设置初始主频率比k=1.3，将构造好的辅助信号作为额外通道信号，用MEMD算法对新的信号进行处理。

(3)使用皮尔逊相关系数选择与原始信号相关最大的两阶IMF，并求其EEMD能量熵的平均值。

(4)主频率比k+0.1，重复步骤(2)、步骤(3)，更新并得到最小的EEMD能量熵，直到k=2.5。

(5)EEMD能量熵最小对应的主频率比k值为最佳主频率比，重新设置辅助信号，并用MEMD算法对新的信号进行处理。

4 仿真试验

在信号分解方面，EMD算法存在模式混合现象。MEMD算法能同时处理多元信号，将多元信号分解成同一个阶次具有相同频带范围的几个IMF组，但继承了EMD算法存在模式混合现象的缺点。NA-MEMD算法能够减少模式混合现象，然而噪声通道上的噪声会泄漏到原始信号通道上，干扰算法的分解性能。本文提出的ISA-MEMD算法能减少噪声的干扰，减少模式混合现象。采样模拟的多元信号验证ISA-MEMD算法的优异性能，仿真信号如下：

S1=0.6sin(2f1πt)+sin(2f2πt)+1.2sin(2f3πt)

S2=0.7sin(2f1πt)+sin(2f2πt)+1.2sin(2f3πt)

S3=0.8sin(2f1πt)+sin(2f2πt)+1.1sin(2f3πt)

本文取f1=45 Hz，f2=70 Hz，f3=140 Hz，采样长度为1024，采样频率fs=1024 Hz。在仿真信号上加入白噪声，分别采用MEMD、NA-MEMD、SA-MEMD和ISA-MEMD将信号分解成IMF。

使用短时傅里叶变换分析仿真信号频谱，选择其中一个通道S1做短时傅里叶变换，其时频图见图2。由图2可看出，信号频率范围为45～140 Hz。主频率比设为1.3～2.5，将辅助信号加入额外通道与原始信号形成Q+1通道信号，用MEMD算法处理新的信号。用相关系数选择相关最大的两阶IMF为第二阶和第三阶，并求其EEMD能量熵平均值。主频率比及对应的EEMD能量熵如图3所示，可见，当主频率比为1.8时第二阶IMF和第三阶IMF的EEMD能量熵平均值最小,因此当辅助信号主频率比设为1.8时算法具有较好的分解性能。

图2 模拟信号短时傅里叶变换时频图

图3 不同主频率比的EEMD能量熵图(仿真)

用MEMD、NA-MEMD、SA-MEMD和ISA-MEMD对信号进行分解得到多组IMF分量。MEMD、NA-MEMD、SA-MEMD和ISA-MEMD的主要IMF频谱图分别见图4～图7,其中，纵坐标数值表示加速度幅值，单位m/s2。

(a)S1 (b)S2 (c)S3

如图4所示，MEMD有明显的模式混合现象，IMF2和IMF3都存在频率140 Hz。不仅IMF5存在频率45 Hz，IMF4中也存在较低幅值的频率45 Hz。如图5所示，NA-MEMD同样存在较为严重的模式混合现象，频率140 Hz既存在于IMF2，也少量存在于IMF3。IMF3和IMF4同时存在频率70 Hz。如图6所示,SA-MEMD的模式混合现象较前两种方法有所改善，但IMF4的主要频率45 Hz少量存在于IMF3。如图7所示，ISA-MEMD的模式混合现象较前三种方法有明显的改善。模拟信号仿真结果表明,ISA-MEMD比MEMD、NA-MEMD、SA-MEMD有更好的分解性能。

(a)S1 (b)S2 (c)S3

(a)S1 (b)S2 (c)S3

(a)S1 (b)S2 (c)S3

5 改进的正弦辅助多元经验模式分解在轴承故障诊断中的应用

为了证明所提方法的有效性，收集滚动轴承外圈的多个故障信号，采样频率fs=10 240 Hz,采样长度为51 200。数据包括从试验设备上不同位置的三个传感器收集的三个通道的信号。图8a所示的试验设备包括变速驱动器、电动机、扭矩传感器/编码器、平行轴齿轮箱、可编程电磁制动器。试验设备的结构图和传感器的位置如图8b所示。

(a)试验台实物图

首先用短时傅里叶变换对采集信号中的一个通道S1进行频谱分析，其时频图见图9。信号频谱范围为20～130 Hz，构造辅助信号。主频率比设为1.3～2.5，用相关系数选择相关最大的两阶IMF为第一阶和第二阶，并求其EEMD能量熵平均值。主频率比及对应的EEMD能量熵如图10所示，可见，第一阶和第二阶IMF能量熵平均值在主频率比为1.4时最小，因此当辅助信号的主频率比设为1.4时算法的分解效果最好。确定好辅助信号的频率比和频率范围，即完成辅助信号的构造。

图9 实际信号短时傅里叶变换时频图

图10 不同主频率比的EEMD能量熵图(试验)

用MEMD、NA-MEMD、SA-MEMD和ISA-MEMD对信号进行分解得到多组IMF分量。MEMD、NA-MEMD、SA-MEMD和ISA-MEMD的主要IMF频谱如图11～图14所示。

(a)S1 (b)S2 (c)S3

(a)S1 (b)S2 (c)S3

(a)S1 (b)S2 (c)S3

(a)S1 (b)S2 (c)S3

如图11所示，MEMD分解的主要IMF分量有明显的模式混合现象，IMF1和IMF2都存在二倍故障特征频率88 Hz。故障特征频率44 Hz同时存在于IMF2和IMF3。如图12所示,NA-MEMD的模式混合现象较MEMD有所改善，但故障特征频率88Hz同时存在于IMF4和IMF5。如图13所示，SA-MEMD的模式混合现象比NA-MEMD和MEMD都轻微，但二倍特征频率88Hz明显存在于IMF1。如图14所示,ISA-MEMD分解的IMF组模式混合现象有所改善，IMF2中的二倍故障频率88Hz幅值明显大于前三种方法的幅值。由分析结果可知,ISA-MEMD的模式混合现象比MEMD、SA-MEMD和NA-MEMD更轻微。试验数据的分解结果验证了所提方法分解性能优于MEMD、SA-MEMD和NA-MEMD的结论。

6 结论

(1)改进的正弦辅助多元经验模式分解(ISA-MEMD)算法克服了正弦辅助多元经验模式分解需要根据经验去选择最佳分解性能对应的辅助信号主频率比的缺点，该算法有较好的分解性能，明显地减少模式混合现象，即最大程度地保持频率的原始幅值，有效地提取故障特征频率，因此ISA-MEMD算法的分解性能要优于传统的多元经验模式分解算法。

(2)采用短时傅里叶变换算法来确定原始信号的频谱范围，避免在构造辅助信号时引入冗余频率，影响算法的分解性能。

(3)提出以最小EEMD能量熵为准则，自适应地选择对应分解结果最佳的主频率比，从而实现辅助信号主频率比参数择优。