考虑电流振铃特性的悬浮电磁铁等效电路模型
2022-06-22张昆仑
梁 达 ,张昆仑 ,肖 嵩
(1.西南交通大学磁浮技术与磁浮列车教育部重点实验室,四川 成都 611756;2.西南交通大学电气工程学院,四川 成都 611756)
磁悬浮列车具有低噪、环保、紧凑和轻量化等优点,是一种可以满足人类对出行安全性、可靠性和快速性要求的新型载运系统.根据悬浮方式的不同,磁浮列车主要分为电磁悬浮和电动悬浮.电磁悬浮可以实现静态悬浮,是目前商业运营磁浮线中广泛采用的技术方案[1].电磁悬浮系统主要由悬浮电磁铁、悬浮斩波器和悬浮控制器组成[2].
悬浮电磁铁电流在悬浮斩波器的开关动作时刻伴随着严重的振铃现象.电流振铃的频率远高于开关频率,它会为电磁悬浮系统造成以下危害:
1) 增加悬浮电磁铁和开关器件的电压应力.因为高频电流振铃经过悬浮斩波器流入悬浮电磁铁,快速变化的电流在功率环路(不包含悬浮电磁铁)的等效电感(器件封装寄生电感,引脚寄生电感以及印制电路板走线寄生电感)上感应出较大电压振铃[3].由于直流侧供电电压恒定,最终导致悬浮电磁铁端电压和开关器件电压发生振铃.从而增大悬浮电磁铁和开关器件的电压应力,加速悬浮电磁铁和开关器件老化进程.2) 增大开关损耗.因为当快速变化的电流通过MOSFET的共源极寄生电感时,其负反馈作用会导致开关管导通时间和关断时间延长[4],从而增加开通损耗和关断损耗.3) 造成电磁干扰(electromagnetic interference,EMI).因为电流振铃频率远高于开关频率,开关暂态过程中的较大的电压变化率和电流变化率都是EMI干扰的根本来源[5].在电磁悬浮系统中,悬浮控制器、辅助电源以及网络传输模块均与悬浮斩波器集成在悬浮控制箱中,因此,电流振铃引起的远场干扰可能影响这些电子电路的正常工作,从而使悬浮控制箱难以通过电磁兼容测评.4) 影响悬浮控制效果.因为高频电流振铃会被悬浮电磁铁的等效电容旁路,对悬浮系统的主磁通和电磁力没有贡献,然而该振铃信号会被悬浮控制器的采样系统收集,直接参与悬浮控制算法[6],从而影响悬浮控制器输出.因此,为了能够提出有效的悬浮电磁铁电流振铃抑制措施,首要任务是研究其产生机理.
目前,对电磁悬浮系统的研究主要集中在对不同悬浮控制算法[7]、悬浮斩波器拓扑[8]以及悬浮电磁铁结构优化[9]等方面,没有相关文献对悬浮电磁铁电流振铃现象进行专门研究.在电力电子变换器领域,普遍认为开关振铃现象是由于功率回路中的寄生电感和寄生电容形成LC振荡腔,在开关动作时刻所产生的较大电压变化率和电流变化率激励作用下,电感中储存的磁场能量和电容中储存的电场能量发生交换而形成的[10].许多学者已经从开关器件模型的角度出发,对开关支路的振铃进行了深入研究,但研究过程中将感性负载理想化为恒流源,即认为开关瞬间感性负载电流恒定[11],显然,这种假设在电磁悬浮系统中并不合理.因此,上述研究中得到的结论不完全适用于电磁悬浮系统.本文从悬浮电磁铁等效电路的角度出发,研究其电流振铃的产生机理.
1 悬浮电磁铁的LRC阻抗网络
图1给出了中低速磁浮列车电磁悬浮系统的实现原理及悬浮斩波器和悬浮电磁铁结构.

图1 中低速磁浮列车电磁悬浮系统组成Fig.1 Composition of the electromagnetic suspension system in medium-low speed maglev trains
图1(a)中:i表示悬浮电磁铁电流,z、v表示悬浮气隙和气隙加速度.在该电磁悬浮系统中,悬浮电磁铁安装在轨道下方,悬浮控制器收集i、z和v信号,并通过特定的算法对上述信号进行处理,输出脉宽调制(pulse width modulated,PWM)信号驱动悬浮斩波器工作,最终实现对悬浮力的调节.图1(b)中:Udc表示悬浮斩波器的供电电压,S1、S2为全控型开关器件(如 IGBT、MOSFET或 SiC等),D1、D2为续流二极管.为了实现最快电流响应速度,悬浮斩波器采用S1和S2同时通断的工作模式.图1(c)中:悬浮电磁铁的铁芯为实心导体,绕组为矩形截面铝线,U型悬浮电磁铁和F型轨道配合可实现自导向.
将悬浮电磁铁的每匝绕组视为一个独立的导体单元,则任意两匝绕组间存在寄生电容效应.但考虑到相邻绕组间(同层相邻绕组间和非同层相邻绕组间)的寄生电容远大于对角相邻绕组间和非相邻绕组间的互感和电容效应,在忽略后者的条件下,悬浮电磁铁可以被抽象为图2所示的单端口LRC无源阻抗网络.其中,红色虚线框部分表示电磁铁绕组,tnm(n=1,2,···,N;m=1,2,···,M) 为悬浮电磁铁第n层的第m匝绕组,N为电磁铁绕组层数,M为电磁铁每层绕组匝数.Uc(s)和I(s)分别为悬浮电磁铁电压和电流的象函数,s为象函数的自变量.Z(s)和Y(s)分别为悬浮电磁铁的策动点阻抗和策动点导纳.悬浮电磁铁任意两匝绕组之间通过电感、电阻、电容或其组合电路连通.假设悬浮电磁铁LRC阻抗网络的内部支路数为B,Ub(s)和Ib(s)(b=1,2,···,B)分别为第b支路电压和电流的象函数,Lb、Rb和Cb分别为第b支路的电感、电阻和电容.

图2 悬浮电磁铁的LRC阻抗网络Fig.2 LRC impedance network of a suspension electromagnet
1.1 策动点函数分析
图2中,Z(s)可表示为

这里规定Uc(s)与I(s)方向相反,Ub(s)与Ib(s)方向相同.则由特勒根定理或复功率平衡得
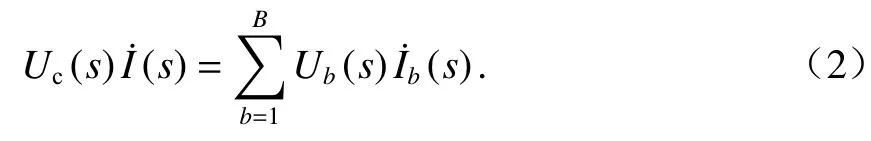
将式(2)代入式(1)得悬浮电磁铁的策动点阻抗为
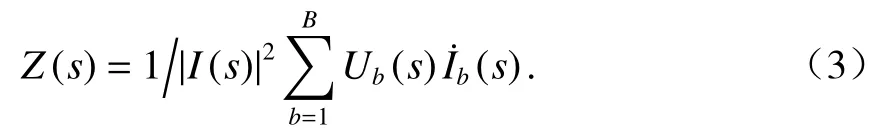
由欧姆定律得第b支路的电压为

将式(4)代入式(3),则Z(s)可表示为

定义式(6)所示的能量函数:
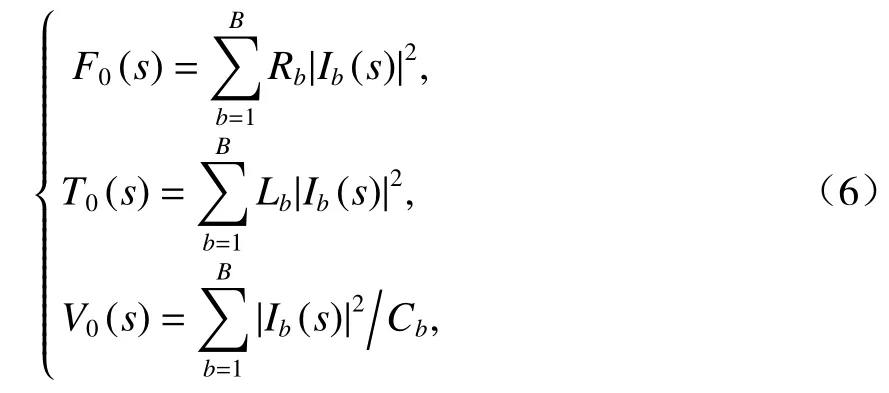
式中:F0(s)、T0(s)和V0(s)分别为与LRC网络中电阻、电感和电容相关的能量函数.
在正弦稳态条件下,即当s=jω时(ω为角频率),式(6)中F0(s)、T0(s)和V0(s)可以表示为

式中:P、Wm和We分别为悬浮电磁铁LRC阻抗网络的有功功率、平均磁场储能和平均电场储能.
对于无源LRC网络,在整个复平面上能量函数不小于0,即

Z(s)和Y(s)可分别用能量函数表示为
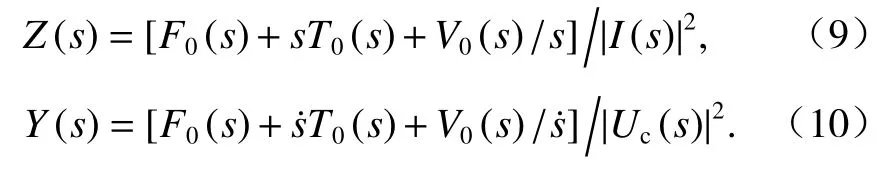
Z(s)和Y(s)统称为悬浮电磁铁的导抗函数,后文用G(s)统一表示.
1.2 导抗函数零极点分布规律
将s=σ 代入式(9),得

将s=σ+jω代入式(9),两端取实部得

由式(11)可知,当自变量s为实数时,Z(s)也为实数,即s面的实轴变换为Z(s)面的实轴.由式(12)可知,当 Res=σ≥ 0 时,ReZ(s) ≥ 0,即s的右半闭面变换到Z(s)的右半闭面.因此,根据复变函数知识可知Z(s)为正实函数,具有以下性质[12]:1)Z(s) 的右半平面是解析的,即Z(s)的极点不可能落在右半平面;2)Z(s)在右半平面不存在零点;3)Z(s)在虚轴上若有极点或零点,只能是一阶;4) 设Z(s) =N(s)/D(s),N(s)和D(s)分别为Z(s)的分子多项式和分母多项式,则N(s)和D(s)的最高次幂之差和最低次幂之差均不超过1;5)Z(s)在虚轴上的实部为非负数,即 R eZ(jω)≥ 0.则Z(s)的一般形式为
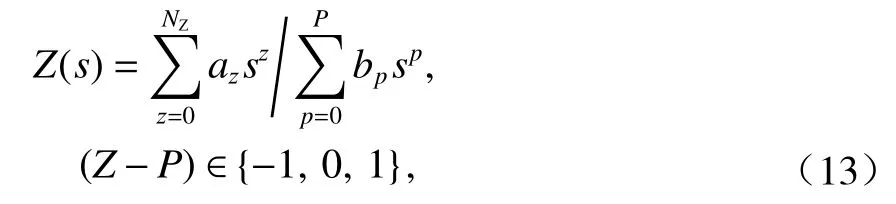
式中:az和bp分别为分子多项式和分母多项式的系数,均为正实常数;NZ为分子多项式的最高次数;P为分母多项式的最高次数.
根据式(9)可知,Z(s)的零点满足

因此,Z(s)的零点可以表示为
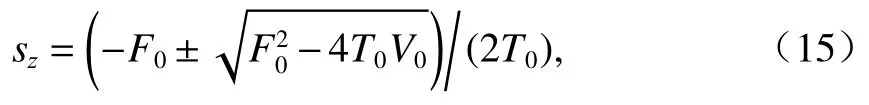
式中:T0、F0和V0即T0(s)、F0(s)和V0(s).
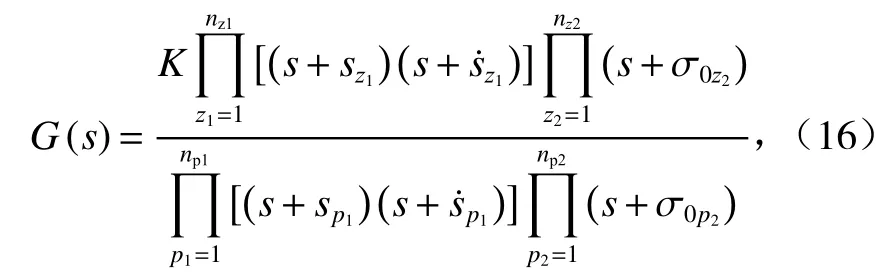
式中:K为比例因子; σ0z2为G(s)的第z2个实数零点;sz1和为G(s)的第z1对共轭复数零点; σ0p2为G(s)的第p2个实数极点;sp1和为G(s)的第p1对共轭复数极点;nz1为G(s)的共轭复数零点的对数;nz2为G(s)的实数零点个数;np1为G(s)的共轭复数极点的对数;np2为G(s)的实数极点个数.
复数极点和零点可以展开为
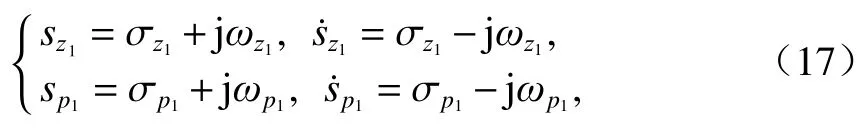
式中: σz1和 jωz1分别为sz1的实部和虚部; σp1和jωp1分别为sp1的实部和虚部.
根据正实函数的性质,有

2 悬浮电磁铁等效电路
悬浮电磁铁电流的零状态响应等于导纳Y(s)乘以激励,因此,I(s)的单位阶越响应可以表示为式(19).
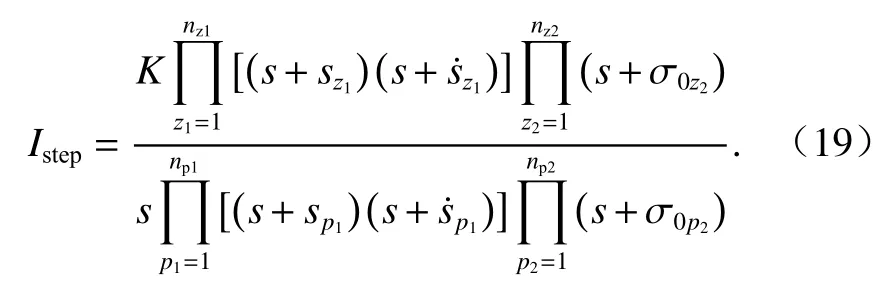
零状态的悬浮电磁铁在单位阶跃电压激励条件下,绕组的初始电流为0,电压突变瞬间产生电流振铃,且电流振铃逐渐衰减,电流终值为1/Rdc,Rdc为悬浮电磁铁的直流电阻.由初值定理得
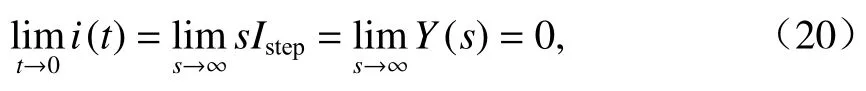
式中:t为时间.
因此,Y(s)的分母多项式的次数高于分子多项式次数.则对于Y(s)有

Istep可以展开为
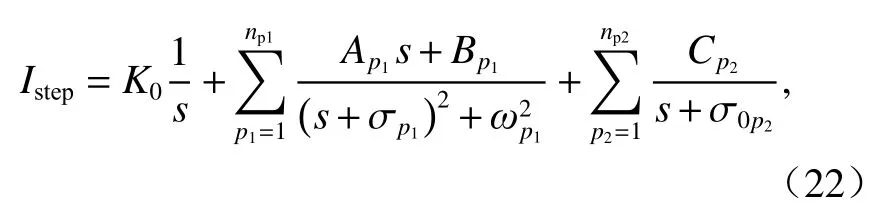
式中:K0、Ap1、Bp1和Cp2均为常系数.
对式(22)进行Laplace反变换得
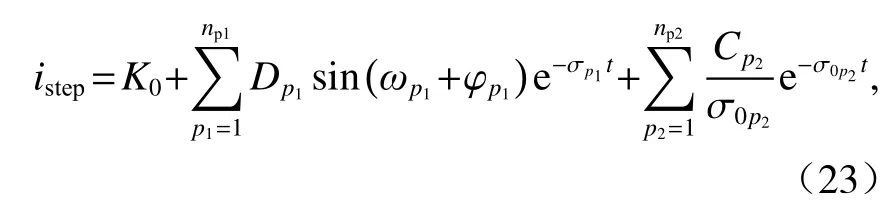
式中:istep为电流单位阶跃响应的时域函数;Dp1为常系数; φp1为相位.
Istep的极点类型决定了其时域波形,每个负实数极点对应一项指数衰减波形,每对共轭复数极点对应一项衰减振荡波形.istep开关动作瞬间的电流振铃说明Istep至少含有一对共轭复数极点;进一步考虑到istep由初值按指数规律变化至终值,则Istep的分母多项式中至少含有一个实数极点.综上所述,Y(s)的最简表达式中包含3个极点(一对共轭复数极点和一个实数极点)和两个零点.则Y(s)的最简表达式为
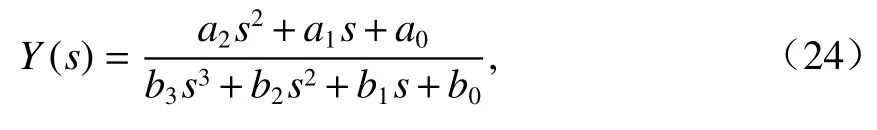
式(24)可以通过图3所示的电路结构实现.因此可以推断,图3所示电路即为悬浮电磁铁的等效电路模型.

图3 悬浮电磁铁等效电路Fig.3 Equivalent circuit of a suspension electromagnet
图3中:Ceq为悬浮电磁铁的等效电容;Rac为由绝缘介质损耗引起的高频等效电阻;Lm为被Ceq旁路的电感;Ls为未被Ceq旁路的电感.其中:Ls、Lm和Rdc构成悬浮电磁铁的低频通路,供低频电流流通;Ls、Ceq和Rac构成悬浮电磁铁的高频通路,供高频振铃电流流通.Ls和Ceq形成了LC谐振腔,开关动作时刻储存Ls中的磁场能量和Ceq中的电场能量交换,形成电流铃,Rac为高频通路提供阻尼,使Ls和Ceq在能量交换交换过程中损耗衰减.iL和ic分别表示流过悬浮电磁铁低频通路和高频通路的电流.悬浮电磁铁等效电路中若没有Ls和Ceq,则不满足电流振铃形成条件;若没有Rac,则电流振铃幅值不会衰减,因此图3为包含了电流振铃特性的悬浮电磁铁等效电路的最简配置.式(24)中的系数可以用图3中电路参数表示为式(25).

3 不同参数对电流振铃的影响
根据图3,悬浮电磁铁电流振铃的单位阶跃响应可以用式(26)表示.

3.1 判别式法分析
由式(26)可知,Icstep(s)的特征方程为
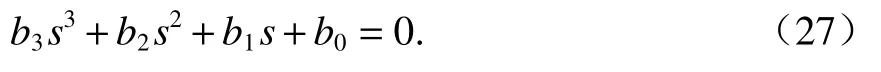
式(27)根值分布的盛金判别式[13]为

当A=C= 0 时,式(27)有一个 3重实根;当Δ<0时,式(27)有3个不相等的实根;当 Δ =0 时,式(27)有3个实根,其中有1个两重根;当Δ>0时,式(27)有1个实根和1对共轭复根,此时悬浮电磁铁在S1和S2动作瞬间存在振铃现象.图4给出了Δ随不同参数变化的曲线.


图4 不同电路参数对Δ的影响Fig.4 Influence of different circuit parameters on Δ
由图4 可知:在Lm、Rdc、Ls和Rac一定的条件下,Δ随着Ceq增大而增大;在Lm、Rdc、Ceq和Rac一定的条件下,Δ随着Ls增大而增大;在Lm、Rdc、Ceq和Ls一定的条件下,Δ随着Rac增大而减小;在Ls、Rdc、Ceq和Rac一定的条件下,Δ随着Lm增大而增大;在Ls、Rac、Ceq和Lm一定的条件下,Δ随着Rdc增大而减小.说明Δ与Ls、Ceq和Lm正相关,与Rac和Rdc负相关.而且,只有在Rac增大过程中,Δ出现负值,即只有在Rac足够大的条件下,悬浮电磁铁不存在电流振铃现象.
3.2 仿真法分析
悬浮电磁铁电流振铃仿真模型如图5所示.其中Iref为目标电流.设计PI电流控制器,使悬浮电磁铁电流追踪目标电流.仿真模型中 S1、S2和 D1、D2为理想元件,导通管压降为0,Iref= 2 A,Udc= 50 V.

图5 悬浮电磁铁电流振铃仿真模型Fig.5 Current ringing simulation model of a suspension electromagnet
为了研究 Ceq、Ls、Rac、Lm和Rdc对电流振铃的影响,通过控制变量法进行模型仿真.仿真参数设置如表1所示.各种条件下所得悬浮电磁铁电流振铃波形(S1、S2导通时刻)分别如图6所示.其中:p0表示S1、S2动作前电流的稳态值;p1~p4分别表示不同仿真条件下,变化参数不同取值时瞬态电流的最大峰值.

表1 仿真参数设置Tab.1 Sinulation parameter setting
由图6(a)可知:在仿真条件 1下,Ceq为 0.5、1.0、2.0 nF和4.0 nF时对应的悬浮电磁铁电流振铃峰值分别为0.90、1.20、1.90 A和2.50 A,振铃频率分别为 3.175、2.222、1.587 MHz和 1.111 MHz.因此,当Lm、Rdc、Ls和Rac一定时,随着Ceq增大,电流振铃峰值增加,振铃频率减小.此外,Ceq变化对振铃衰减速度的影响较小.由图6(b)可知:在仿真条件2下,Ls为 5.0、10.0、20.0 μH 和 40.0 μH 时对应的悬浮电磁铁电流振铃峰值分别为1.60、0.95、0.70 A和0.50 A,振铃频率分别为 2.222、1.587、1.111 MHz和0.794 MHz.因此,当Lm、Rdc、Ceq和Rac一定时,随着Ls增大,电流振铃的峰值减小,振铃频率减小;此外,随Ls增大,振铃衰减速度减缓.由图6(c)可知:在仿真条件 3下,Rac为 5.0、20.0 Ω和 50.0 Ω时对应的悬浮电磁铁电流振铃峰值分别为1.40、1.20 A和 0.90 A,振铃频率均为 2.222 MHz;Rac为 200 Ω时,电流暂态波形为电流脉冲,峰值为0.40 A.这是由于当Rac为 200 Ω 时,判别式Δ< 0.此外,当Lm、Rdc、Ls和Ceq一定时,随着Rac的增大,电流振铃幅值减小,振铃衰减时间缩短.由图6(d)~(e)可知:电感Lm和电阻Rdc对悬浮电磁铁电流振铃峰值、频率及衰减时间的影响很小.综上可知:悬浮电磁铁的电流振铃特性主要由Ls、Ceq和Rac决定.尽管仿真中所用电路参数可能与实际电路参数不一致,仿真结果仍然可以说明不同参数对电流振铃的影响.

图6 不同参数条件下悬浮电磁铁的电流振铃波形Fig.6 Current ringing waveforms of suspension electromagnet with different parameters
4 小电磁铁电流振铃仿真和实验
悬浮电磁铁电流振铃测试系统如图7所示.用LCR阻抗测量仪测量计算得到悬浮电磁铁的参数为Lm=6.8 mH,Ceq=308.0 pF,Rdc=1.0 Ω,Ls=3.8 μH,Rac=20.0 Ω.示波器 RTM2032和TSD3054B分别用于观测悬浮电磁铁的电压和电流波形,TCP303和TCPA300分别为电流探头和电流探头放大器.悬浮斩波器的 S1、S2采用 IRFP250N 场效应管,D1、D2采用D92-03肖特基二极管,控制器为TMS320 F28335 DSP,PWM驱动器为KA962F模块.直流母线电压Udc=50.0 V,目标电流Iref=2.00 A,开关频率为10 kHz.

图7 悬浮电磁铁电流振铃测试系统Fig.7 Current ringing test system for suspension electromagnet
首先,将上述悬浮电磁铁的参数代入图5所示的仿真模型,得到悬浮电磁铁电流和电压仿真波形分别如图8(a)和图8(b)所示.图8(a)中:ton为 S1、S2导通时刻;toff为 S1、S2关断时刻.由图8(a)可知:仿真所得悬浮电磁铁电流纹波幅值为0.37 A,S1、S2导通和关断时刻产生电流振铃的峰峰值为1.40 A,振铃频率约为4.500 MHz.S1、S2导通和关断时刻所产生电流振铃的幅值和衰减速度相同,方向相反.由图8(b)可知:仿真所得悬浮电磁铁电压uc为理想的 PWM 波形,S1、S2导通阶段,uc= 50.0 V,S1、S2关断阶段,uc= -50.0 V.
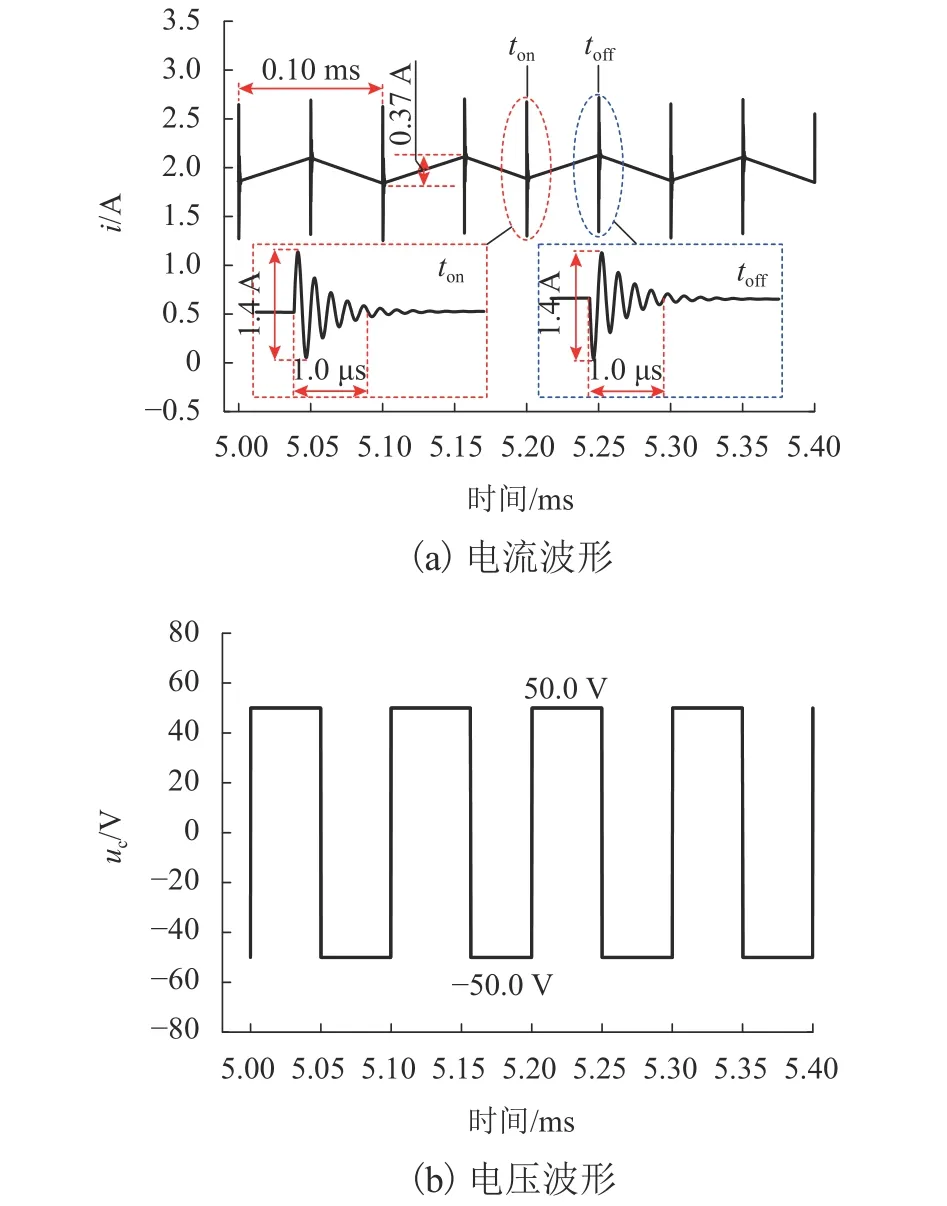
图8 悬浮电磁铁电流和电压的仿真波形Fig.8 Simulated current and voltage waveforms of suspension electromagnet
相同条件下,悬浮电磁铁电流和电压实验波形分别如图9(a)和图9(b)所示.由图9(a)可知:实验所得悬浮电磁铁电流纹波幅值为0.33 A,S1、S2导通和关断时刻产生电流振铃的峰峰值为1.12 A,振铃频率约为4.000 MHz,S1、S2导通和关断所产生电流振铃方向相反.由图9(b)可知:实验所得悬浮电磁铁电压波形在S1、S2导通和关断时刻存在20.0 V的电压过冲.此外,S1、S2导通阶段,uc的平均值为44.0 V,说明S1和S2的导通管压降为3.0 V;S1、S2关断阶段,uc的平均值为-47.0 V,说明D1和D2的导通管压降为1.5 V.

图9 悬浮电磁铁电流和电压的实验波形Fig.9 Experimental current and voltage waveforms of suspension electromagnet
对比图9(a)和图8(a)可知:实验所得悬浮电磁铁电流纹波的幅值比仿真结果低9.7%,实验所得悬浮电磁铁电流振铃峰峰值比仿真结果小20%,实验所得悬浮电磁铁电流振铃的频率比仿真结果低11%.对比图9(b)和图8(b)可知:实验所得悬浮电磁铁电压波形在S1、S2动作时刻存在电压过冲,而仿真结果不存在电压过冲.这是由于仿真模型忽略了S1、S2和D1、D2的导通压降、导通等效电阻、封装寄生电感以及印制电路板电路寄生电感的影响[14].此外,S1、S2的寄生电容(门极-漏极寄生电容、门极-源极寄生电容和漏极-源极寄生电容)和D1、D2的结电容也会对高频振铃信号产生影响[15].
5 结 论
本文用策动点函数法推导了悬浮电磁铁导抗函数的一般形式,并提出了一种考虑电流振铃特性的悬浮电磁铁等效电路模型.
所提等效电路模型包含低频和高频两种电流通路.流振铃分量主要从高频通路流通,振铃的幅值特性、频率特性和衰减特性由高频通路的等效电感、等效电阻和等效电容决定.
所提悬浮电磁铁等效电路模型可用于仿真和分析悬浮斩波器的暂态特性,也能为悬浮电磁铁电流振铃抑制方案设计提供指导.
由于开关器件寄生电感、寄生电容以及印制电路板线路寄生电感等未建模因素的影响,所提等效电路与实际电路之间存在一定偏差.因此,为了提高模型的准确性,应进一步建立包含上述参数的等效电路模型.此外,可进一步根据所提等效电路设计适用于电磁悬浮系统的电流振铃抑制装置.
