一种叠加随机游走重力模型的链路预测算法

姜万昌,路明明

(1.东北电力大学 计算机学院， 吉林 吉林 132012；2.东北电力大学 吉林省智能电网信息技术工程实验室， 吉林 吉林 132012)

0 引言

链路预测用于蛋白质网络预测[1]、航班风险预测[2]、网络结构优化[3]等领域，揭示网络的结构特性。其中广泛使用的基于网络结构的链路预测算法分为基于局部信息、基于路径和基于随机游走三类算法。第一类基于局部信息算法，其使用最广泛的CN算法(common neighbors)利用节点之间公共邻居节点的数量进行预测[4]。Adamic等[5]利用共同邻居节点的度提出AA算法(adamic-adar)。AA是CN的变型，公共邻居节点的度越大，节点之间存在链路的可能性越小。Lyu等[6]受网络资源分配过程的启发提出与AA算法相似的RA算法(resource allocation)，两者预测效果相近。这些算法不能区分不同公共邻居节点的作用，Liu等[7]提出局部朴素贝叶斯模型LNBCN和LNBRA算法，揭示不同公共邻居节点的不同作用。第一类算法较简单，算法的时间复杂度较低，但只考虑节点或节点之间的公共邻居节点的度，没有结合更多的网络结构信息。第二类基于路径算法中，Katz算法[8]使用2个节点之间的所有路径，通过对路径的长度进行惩罚的方式预测，在许多网络上具有不错的预测效果。但计算节点之间的所有路径会导致算法的时间复杂度高，因此又提出在CN算法和Katz算法之间折衷的LP算法[8]，只利用长度为2和3的路径信息。第二类算法增加节点的路径信息，较第一类算法考虑更多的网络结构特征，但没有利用节点之间的紧密程度度量。第三类基于随机游走算法中，RWR(random walk with restart)算法[9]从源节点随机游走一步后有一定概率在下一时刻回到源节点，利用游走稳定达到目的节点时的概率进行预测计算。这样计算的复杂度较高，邵豪等[9]用节点度量化随机游走转移概率，只考虑几步随机游走提出LRW算法(local random walk)。为提高目标节点与附近节点之间转移概率，在LRW上叠加局部游走步数得到SRW(superposed random walk) 算法[9]。第三类算法精度较高，但只关注一种结构特征假设适用于所有网络，其预测性能在不同网络上具有不稳定性。这三类算法在真实的网络数据集上进行对比实验，吕琳媛[10]的研究结果表明第三类基于随机游走的算法具有较高的准确性，尤其是基于局部随机游走的算法具有更高预测精确度。但对于具有局部高聚集程度的网络，局部随机游走算法没有考虑网络局部节点与邻居节点的紧密程度。

链路预测中节点与邻居节点的紧密程度可以用聚类系数衡量。研究表明，网络的聚类系数能有效提高链路预测效果[11]。Wu等[12]提出基于节点聚类系数的CCLP算法，但没有考虑邻居节点的度。高杨等[13]在此基础上结合邻居节点的度，提出一种结合节点度和聚类系数的链路预测NDCC算法。陈紫扬等[14]认为NDCC算法只考虑单层度，信息不全面，提出结合二层节点度和聚类系数的链路预测TDNCC算法，虽然提高了基于局部信息的算法性能，并且与基于随机游走的算法相比性能较优，但不适于具有局部高聚集程度的网络。

综上考虑，在具有局部高聚集程度的网络中，针对局部随机游走算法可能无法区分网络中存在度和聚类系数均高的节点之间预测效果的问题，在局部随机游走的基础上，结合公共邻居节点的聚类系数，并对游走步数进行叠加计算，在全局网络上利用重力模型，提出一种叠加随机游走重力模型链路预测算法。

1 链路预测算法

结合邻居节点的度和聚类系数，改进叠加随机游走的转移概率，引入重力模型，提出一种叠加随机游走重力模型的链路预测算法。

1.1 改进的随机游走转移概率

对于具有局部高聚集程度的网络，等概率随机游走不能很好地反映这种网络结构，预测效果不佳。因此，本节结合聚类系数和RA算法，构建改进的随机游走转移概率矩阵。

网络G=(V,E,A)，V表示G的节点集，N=|V|表示G的节点数，E表示G的边集，A=(axy)N×N表示G的邻接矩阵。若G中节点满足(x,y)∈E，axy值为1，否则axy值为0。当G中存在度和聚类系数均高的节点v′，其构成的节点集V′满足V′={v′|v′∈V,kv′>0.6·Maxdegree,Cv′>0.6}且|V′|>0.1·N时，G是具有局部高聚集程度的网络，其中|V′|表示v′的数量，kv′表示v′的度，Maxdegree表示G的最大度数，Cv′表示v′的聚类系数。

构造随机游走模型并设置初始状态，将一个walker放置在网络G的任意节点x处，规定walker以节点之间的相似性作为转移概率同时进行随机游走，游走的每一步的选择相互独立。受Node2vec算法[15]的启发，按照节点x与节点y有无公共邻接节点分2种情况，分别计算walker从节点x到节点y的转移概率：

1) 当节点x与节点y无公共邻居节点，满足x的邻居节点集Γ(x)与y的邻居节点集Γ(y)交集为空，即Γ(x)∩Γ(y)=∅时，根据y的度可以区分walker游走到x的不同邻居节点的转移概率。考虑节点x、节点y的度以及两者之间的连接情况，利用A，定义转移概率如式(1)所示。

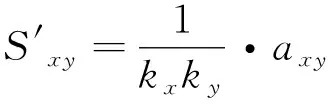
(1)

式中：axy表示x与y是否连接；kx、ky分别表示x、y的度。

2) 当节点x与节点y有公共邻居节点时，公共邻居节点的聚类系数反映x和y周围节点的聚集程度，但当节点之间的公共邻居节点具有相同的聚类系数时，不能区分节点之间的相似性，故将公共邻居节点的度与聚类系数结合；RA算法能有效地反映x与y的公共邻居节点影响x到y的资源分配情况，则定义转移概率如式(2)所示。

(2)

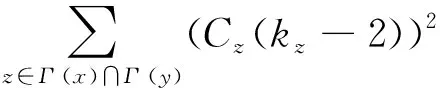
综合上述2种情况，定义网络G改进的随机游走转移概率如式(3)所示。

(3)

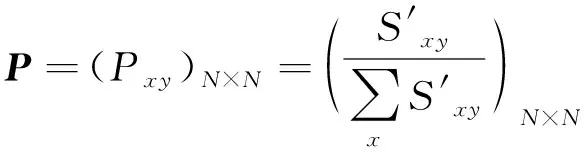
(4)

1.2 叠加局部随机游走

局部的随机游走与全局的随机游走相比，在时间复杂度较小时能获得较高的精度，故在网络G中按照改进的随机游走转移概率进行有限步数的局部随机游走。为了充分结合G的结构特征，进行叠加局部随机游走。

在网络G中，walker从任意节点开始随机游走t步到达G上其余节点的转移概率向量为:

πx(t)=PT·πx(t-1)

(5)

式中：πx(0)=ex表示walker的初始状态，ex是一个1×N的行向量，该向量第x列处元素为1，其余全为0；P表示改进的随机游走转移概率矩阵；T表示矩阵转置。

假定任意节点x的初始资源分布为x的度kx，则节点x与任意节点y基于t步局部随机游走的转移概率为：

(6)

将前t步的结果相加，得到节点x与任意节点y基于t步叠加局部随机游走的转移概率为:

(7)

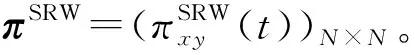
1.3 叠加随机游走重力模型

重力模型已用于定义节点的吸引力识别复杂网络中的关键节点[17]，可以从全局网络的角度分析节点之间的关系影响，故引入重力模型，设计叠加随机游走重力模型，计算节点之间的相似性。

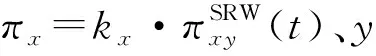
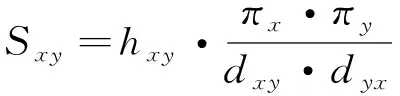
(8)

根据计算G的节点之间的相似性，最后得到叠加随机游走重力模型节点相似性矩阵为S=(Sxy)N×N。

1.4 叠加随机游走重力模型的链路预测算法

使用叠加随机游走重力模型，得到叠加随机游走重力模型链路预测算法(link prediction algorithm based on superimposed random walk gravity model，SRWG)，其中步骤1)—6)初始化改进的随机游走转移概率矩阵S′、叠加局部随机游走的转移概率矩阵πSRW、叠加随机游走重力模型节点相似性矩阵S等；步骤7)—10)用式(3)和式(4)计算S′并标准化处理得到改进数的随机游走转移概率矩阵P；步骤11)—17)用式(5)—(7)计算得到基于步叠加局部随机游走的转移概率矩阵πSRW；步骤18)—21)用式(8)计算叠加随机游走重力模型节点相似性矩阵S。

SRWG算法如下:

输入:网络G的邻接矩阵A=(axy)N×N、随机步长t输出:叠加随机游走重力模型节点相似性矩阵S=(Sxy)N×N

1) 初始化改进的随机游走转移概率矩阵S′←0N×N；

2) 初始化G节点间的最短路径矩阵D←(dxy)N×N；

3) 初始化G节点间的连通度矩阵H←(hxy)N×N；

4) 初始化基于步叠加局部随机游走的转移概率矩阵πSRW←IN×N；

5) 初始化叠加随机游走重力模型节点相似性矩阵S←0N×N；

6) 初始化G节点间的公共邻居节点度总数矩阵B←A*AT；

目前我国没有正式的养老地产项目用地的供应政策。养老地产的建设用地优惠力度表现得并不明显。从各地实践看，截至2012年底，北京市、四川省、吉林省、山东省、广东省陆续采取“养老综合用地招拍挂”政策，养老用地被政府纳入土地利用总体规划。在用地上，优先安排符合规划的养老服务设施的建设用地。

7) Forx←1 toΝdo 7)—10)

8) Fory←1 toΝdo

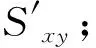
10) 用式(4)标准化处理S′得到P；

11) Forx←1 toΝdo 11)—17)

12) 迭代t步

13)P代入式(5)中；

14) 用式(5)计算G中walker从任意x开始随机游走t步到达G上其余节点的转移概率向量πx(t)；

15) Fory←1 toΝdo

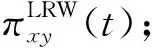
18) Forx←1 toΝdo 18)—21)

19) Fory←1 toΝdo

21) 用式(8)计算G中x与y的相似性Sxy。

1.5 实例计算

斑马网络如图1所示，其平均度为8.222，聚类系数为0.876。网络26个节点中,度大于11且聚类系数大于0.8的节点有14个，故该网络是具有局部高聚集程度的网络。使用斑马网络作为网络实例，用于SRWG算法求解过程的说明。

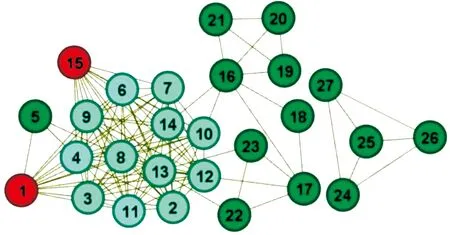
图1 斑马网络

表1的横栏和竖栏分别表示斑马网络的不同的节点，表内的数据表示计算得到的不同节点之间叠加随机游走重力模型节点相似性，对角线的数据表示同一个节点与节点之间的相似性，由于本文算法只计算不同节点之间的相似性，故将同一个节点与节点之间的相似性设为0。

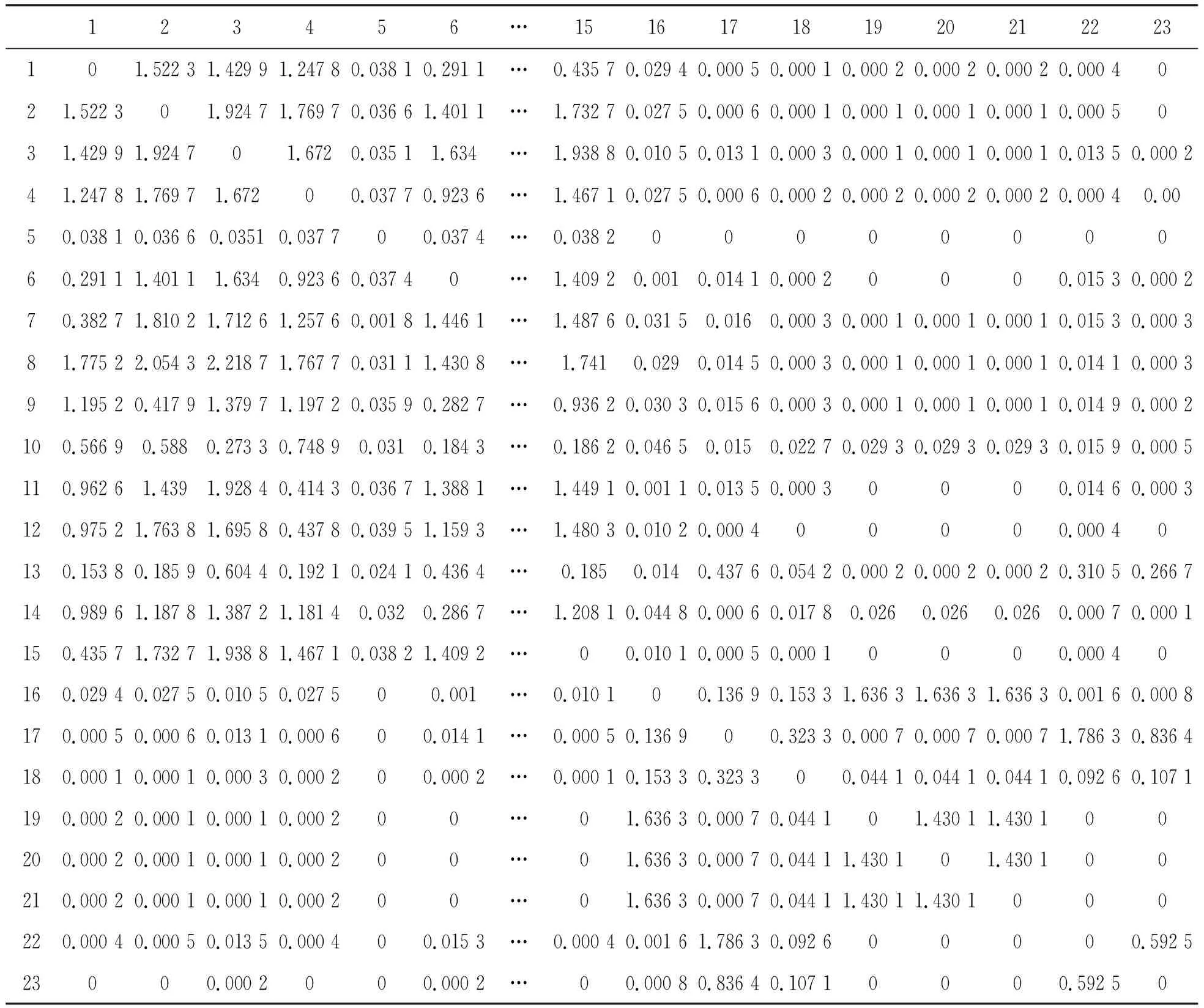
表1 叠加随机游走重力模型节点相似性矩阵S

SRWG算法充分考虑节点的度、聚类系数、节点之间的吸引力等结构特性计算节点之间的相似性。图1中，节点1与节点15之间比节点16与节点23之间的公共邻居多且邻居节点之间的聚集程度大，本文算法得到的叠加随机游走重力模型节点相似性矩阵S中，节点1与节点15之间相似性S1,15=0.435 7，节点16与节点23之间相似性S16,23=0.096，说明本文方法对具有度和聚类系数均高的节点之间可以进行有效的链路预测。

2 实验

2.1 实验设计

选取生物网络、航空网络、社交网络等领域中11个具有不同的平均度和聚类系数的真实网络进行实验，网络数据的统计量信息如表2所示。其中，|V|表示网络的节点数量，|E|表示网络的边数量，〈k〉表示网络的平均度，〈d〉表示网络的平均最短路径，C表示网络的聚类系数，M表示网络的密度，D表示网络的直径。

将SRWG算法与基于局部信息的考虑公共邻居节点的CN和RA算法、基于局部信息的结合朴素贝叶斯模型的LNBCN和LNBRA算法、基于路径的LP和Katz算法、基于随机游走的RWR和SRW算法与基于节点聚类系数的NDCC和TDNCC算法进行预测性能对比，用AUC[18]和Precision[19]指标衡量链路预测结果的精确度。使用Matlab作为实验工具，进行100次独立实验，取平均值，将原网络划分为训练集train和测试集test，其中训练集比例为90%，测试集比例为10%。

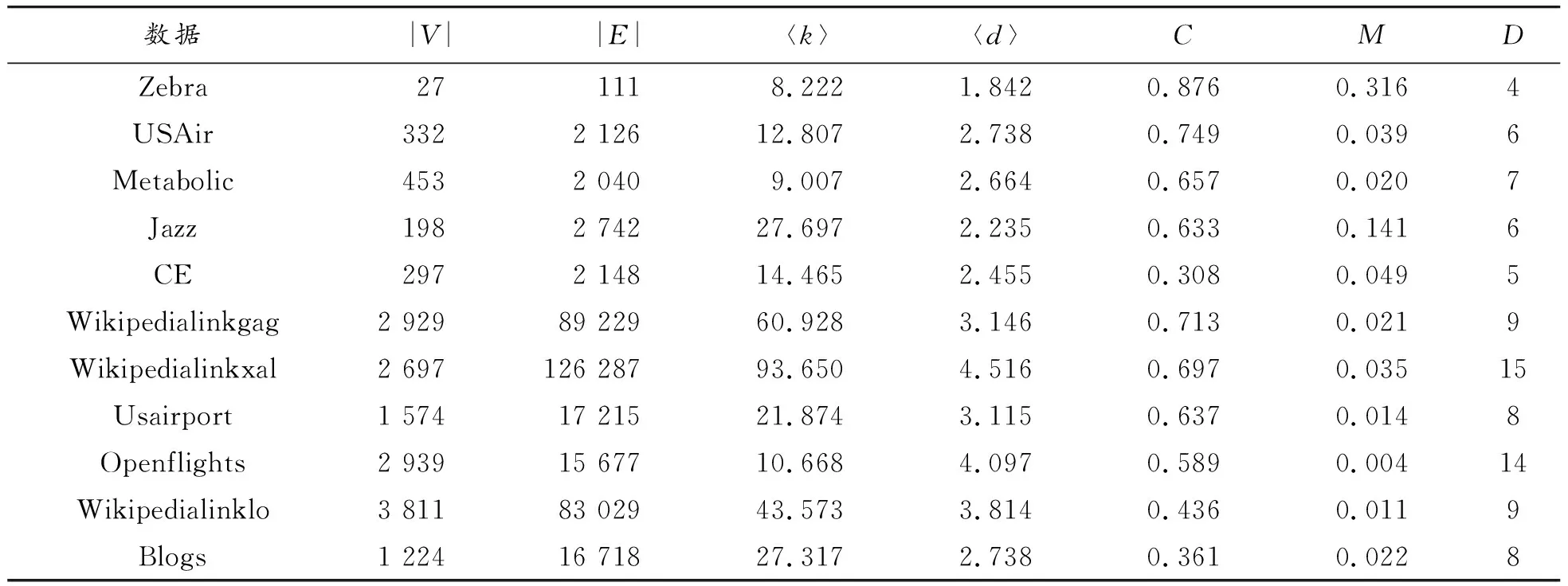
表2 11个真实网络的统计量信息

2.2 AUC和Precision指标分析

将表2中网络按照节点数量是否大于1 000分成2组，前5个为1组，后6个为1组。图2表示前5个网络上各种算法的AUC指标度量情况，图3表示后6个网络上各种算法的AUC指标度量情况。图2和图3中的对比算法分为2个部分，第1部分是CN、RA、LNBCN、LNBRA、LP和Katz算法与本文算法进行比较，第2部分是RWR、SRW、NDCC和TDNCC算法与本文算法进行比较。图4表示2组网络上每种算法的Precision指标度量情况。

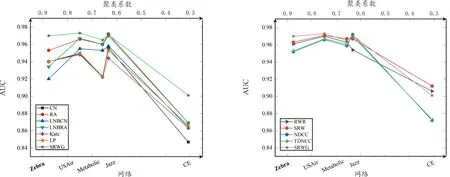
图2 5个网络上各种算法的AUC

图3 6个网络上各种算法的AUC

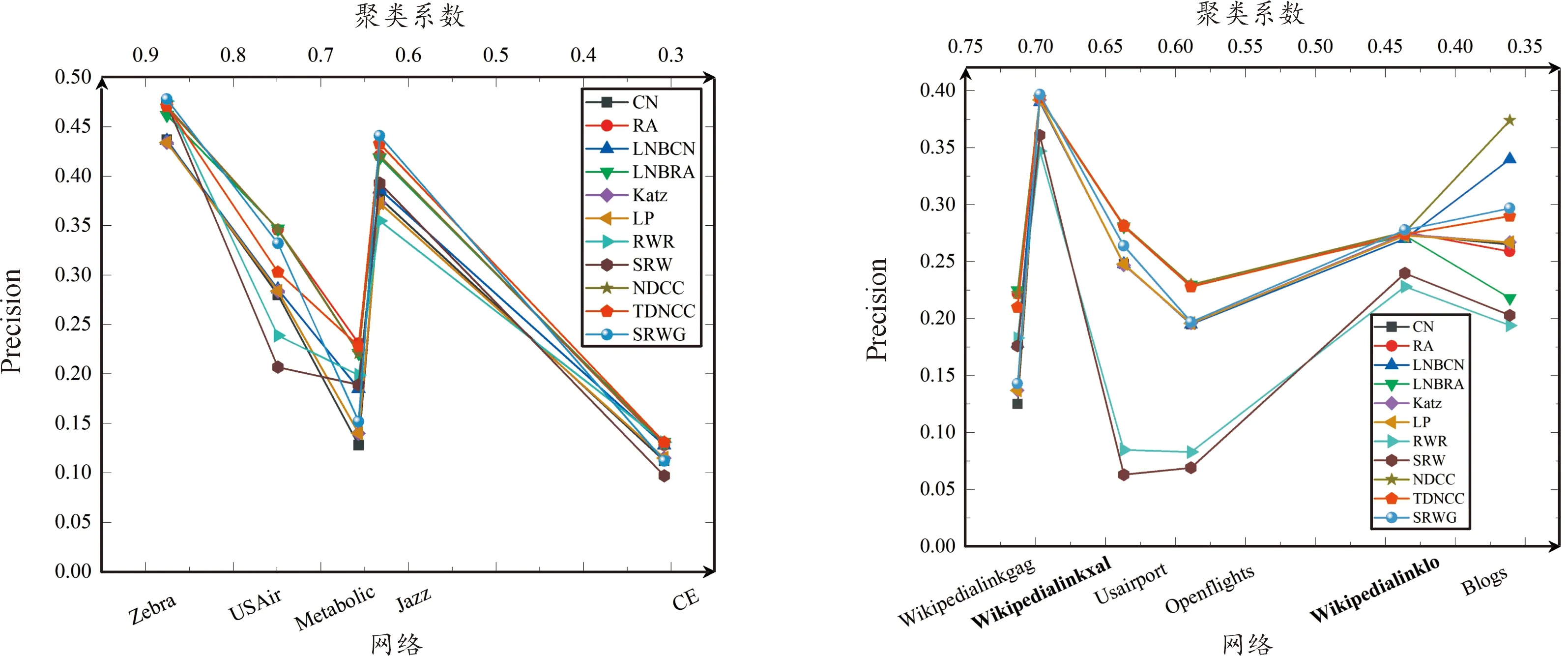
图4 11个网络上各种算法的Precision

图2、图3和图4的坐标下轴表示不同的网络，上轴表示网络的聚类系数，左轴表示AUC或Precision指标数值。与其他算法的AUC指标相比，SRWG算法在其中8个网络上表现最佳，在Metabolic、CE网络上排名第2、在Wikipediagag网络上排名第3；基于Precision指标，SRWG算法在其中4个网络上Precision值最大，表现最佳，在Blogs、USAir网络上排名第3，在Usairport、Openflights网络上排名第5，其余网络上表现较差。

图2和图3中，随着聚类系数的减小，各算法的AUC指标的变化趋势并不会呈现明显下降。当聚类系数大幅下降时，预测效果会明显下降，当聚类系数下降幅度在有限的小范围内，预测效果会发生波动。当2组网络中的聚类系数相差不大时，网络的密度越小，AUC值越大，SRWG算法和基于随机游走的算法与其他算法相比，AUC值提高较多。

图2和图3中，SRWG算法左侧图的折线都在CN、RA、LNBCN、LNBRA、LP和Katz算法的折线上面，右侧图的折线都在NDCC和TDNCC算法的折线上面，但右侧图的SRWG算法与RWR和SRW算法的折线有相交部分。在11个网络中，SRWG算法较CN、RA、LNBCN、LNBRA、LP、Katz、NDCC、TDNCC算法的AUC指标分别平均提高2.6%、1.4%、2.3%、1.6%、2.1%、1.8%、1.4%和1.2%。相对RWR和SRW算法，SRWG算法对于不同聚集程度的网络的AUC指标表现各有差异，具体分析如下：

Zebra、Wikipediaxal、Wikipedialo网络的平均度较高且聚类系数较高，网络局部具有高聚集程度，SRWG算法与RWR和SRW算法相比分别平均提高了0.9%和0.7%。

虽然USAir、Jazz、Usairport、Openflights、Blogs网络的平均度较高且聚类系数较高，但网络整体聚集程度较为均匀，SRWG算法略优于RWR和SRW算法，分别平均提高了0.5%和0.2%。

Metabolic、Wikipediagag网络的平均度低且聚类系数较高，CE网络的平均度低且聚类系数低，都不存在局部高聚集程度，网络整体聚集程度较低，RWR和SRW算法表现最好，相对于SRWG算法分别平均高出0.2%和0.6%。

2.3 度和聚类系数对SRWG算法的AUC指标影响的分析

SRWG算法使用度和聚类系数结合的方式提供节点之间转移概率的贡献，将其作为节点的影响力。图5描述网络中节点的不同程度的度和聚类系数的分布情况，以及度和聚类系数结合下节点的影响力的分布情况，用于分析网络节点的不同程度的度和聚类系数对SRWG算法和其他算法的预测效果的影响。按照SRWG算法与RWR和SRW算法之间的AUC指标差异，分3种情况进行分析。

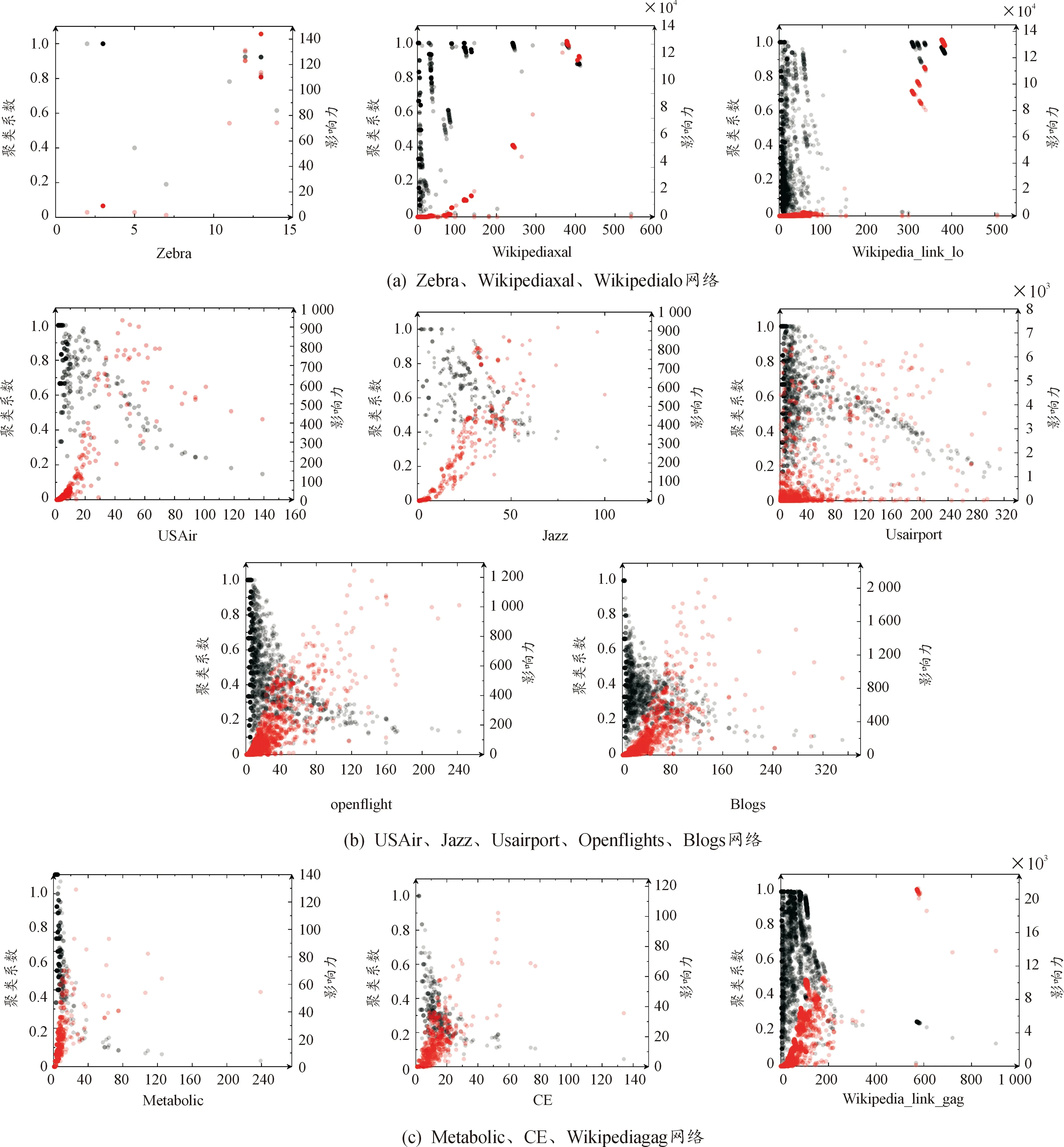
图5 节点的度数与聚类系数和影响力的关系

图5(a)中Zebra、Wikipediaxal、Wikipedialo网络的节点的度和聚类系数主要集中分布在右上部和左下部区域，度高且聚类系数高的节点和度低且聚类系数低的节点较多。这3个网络节点影响力出现不连续的突然增长的上升趋势，度高且聚类系数高的节点的影响力极大，且与度低且聚类系数低的节点相比，节点的影响力差异极大，说明网络中存在很多高聚集程度的节点，所以SRWG算法效果最好。

图5(b)中USAir、Jazz、Usairport、Openflights、Blogs网络的节点的度和聚类系数主要集中分布在中部区域，低度且高聚类的节点数和高度且低聚类的节点数相差不多。这5个网络节点的影响力分布较为分散，呈现均匀的上升趋势，说明网络大部分节点的聚集程度较为均匀，所以SRWG算法略优于RWR和SRW算法。

图5(c)中Metabolic、CE、Wikipediagag网络的节点的度和聚类系数主要集中分布在左上角区域，度低且聚类系数低的节点和度低且聚类系数高的节点较多，没有度和聚类系数均高的节点。这3个网络的节点影响力主要集中分布在左下角区域，节点影响力低，说明网络没有高聚集程度的节点且节点的聚集程度均低，所以RWR和SRW算法优于SRWG算法。

另外，对于上述所有情况中的网络，SRWG算法都优于基于聚类系数的NDCC和TDNCC算法，这说明邻居节点的聚集程度在计算节点相似性起到很大作用。

综上所述，SRWG算法与除RWR和SRW算法的其他算法相比，都可以达到最高的预测精度，且对于具有局部高聚集程度的网络，SRWG算法比RWR和SRW算法表现更好，结果证明SRWG算法是有效的。

3 结论

针对等概率转移的局部随机游走的链路预测算法忽略网络结构，不适用于具有局部高聚集程度的网络的问题，提出一种叠加随机游走重力模型的链路预测算法。该算法充分利用网络结构信息，体现局部范围节点之间相互影响对链路生成的贡献。在随机游走的过程中融合各节点相似性，有效地度量各邻居节点的转移概率。最后针对几组不同聚类系数和平均度的真实网络进行实验，结果表明提出的算法能取得更好的预测效果。

本文中研究的链路预测方法只考虑了无向无权网络，接下来的研究主要是能否将该方法扩用到有向有权网络，从而提高链路预测的精确度。