磁力密度曲线的爬壁机器人统一优化设计
2022-06-18尹海斌曹建国
尹海斌,张 罕,曹建国
(1.湖北省数字制造重点实验室, 武汉 430070;2.武汉理工大学 机电工程学院, 武汉 430070;3.北京科技大学 顺德研究生院, 广东 佛山 528399;4.北京科技大学 人工智能研究院, 北京 100083;5.北京科技大学 机械工程学院, 北京 100083)
0 引言
随着人力成本的增加和科技发展的需求,爬壁机器人大量应用于社会生活的各个领域[1]。它不仅能高效取代人工作业,而且特别适合临空或高危环境[2-7]。无论这些爬壁机器人是负压式、磁吸式、仿生粘附[8-9],还是电极吸附[10]等,它们都属于移动型机器人,需要尽量减小整机质量,否则会影响运动性能。特别是采用电池组供电时,冗余的结构质量不仅不符合节能减排要求,还会降低机器人的续航能力。因此,轻量化设计是爬壁机器人的重点研究内容之一。
爬壁机器人的轻量化设计主要有:一是选择轻质材料实现轻量化设计[11],是一种微观结构优化方法;二是采用拓扑优化减少冗余材料来提高轻量化程度[12],是一种宏观结构优化方法。通过结构优化可以提高爬壁机器人的轻量化程度[13-14],但只考虑结构不考虑电磁动力对结构的影响,不是最优设计方案。因此,还需要考虑电磁动力对轻量化的影响[15-18]。
电磁动力的优化对机电设备轻量化设计有重要意义,与结构之间相互影响、彼此关联。由于电磁动力和传动系统质量之间存在映射关系[19],所以结构优化不仅可以减小结构本身的质量,而且可以降低驱动力矩,进而降低电机的质量,致使机电设备质量进一步减小,这种质量下降的动态过程反过来又会促进结构的优化。因此,同时考虑二者之间的关联性才能最大程度降低整机质量。Yin等[20]通过构建机械臂的结构与动力的统一描述模型,定量描述了结构变量与动力变量之间的关系,利用统一优化方法完成了机械臂的轻量化设计。这种方法可以推广到含有电机动力的机电设备轻量优化设计中,但其只考虑了电机动力,没有考虑磁吸附这类电磁动力。
对于磁吸附爬壁机器人而言,磁吸附也属于电磁动力,是除结构和电机之外需要重点研究的对象。Cai等[21]设计了拥有新型永磁轮的磁吸附爬壁机器人;胡凤菊等[22]设计了行走在压力容器壁上的磁吸附爬壁机器人;丁问司等[23]设计了含有永磁万向轮辅助吸附机构和从动轮浮动机构的磁吸附爬壁机器人。这些设计沿用了传统的集成设计方法,先给出结构后设计磁吸组件和选择电机,但没有进行优化设计。陈勇[24]介绍了一种基于Halbach永磁阵列的可变磁力吸附单元,对其结构参数进行了定量分析和优化。但是,吸附装置中增加了驱动电机和传递齿轮,导致吸附单元质量增加。范召舰[25]利用永磁体磁极同名相对阵列排布方式增大磁吸附力并对主要结构参数进行优化,减小了磁轮质量,却忽略了轻量化的磁轮对受力分析的影响。张大伟等[26]设计了一种带全向永磁轮的微型爬壁机器人,以最小驱动力矩为目标对主要尺寸参数进行了优化,然而没有对机电传动部分做进一步的分析和优化。
针对上述问题,本文中将电机动力与磁吸附力统称为电磁动力,通过建立磁吸附爬壁机器人的结构与电磁动力的统一描述模型,定量分析磁吸附爬壁机器人的结构与电磁动力之间的相互影响规律和爬壁机器人质量分布规律。在此基础上,提出了基于磁力密度曲线的统一优化方法,优化设计了更加轻量的磁吸附爬壁机器人。这一方法将弥补现有磁吸附爬壁机器人轻量优化设计中的不足,进一步拓展了机电设备统一优化设计的适用范围。
1 多学科的统一描述
磁吸附爬壁机器人的电磁动力来源于两大核心模块:磁吸附组件和驱动组件,分别为机器人提供磁吸附力和驱动力矩。对于轻量化设计,同样的电磁力输出,希望电磁力转换部件越轻越好,因此转换部件的优化设计是重点。但是,磁吸附爬壁机器人电磁力转换部件优化会受到结构的影响,反过来又会影响结构的优化。为了弄清楚结构与电磁动力之间如何相互影响爬壁机器人的轻量化设计,需要建立一个能够评估结构与动力之间相互关系的模型,如图1所示。
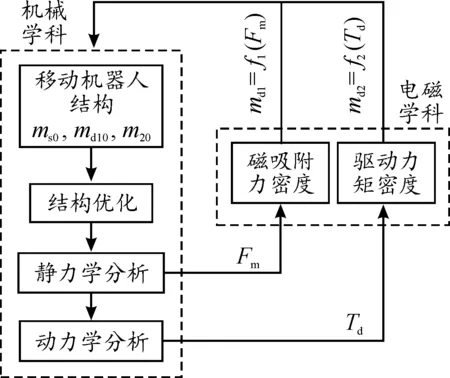
图1 多学科的统一描述
首先,通过结构力学分析可求取一定结构需要的磁吸附力Fm和驱动力矩Td;其次,利用电磁力转换部件的质量与电磁力的映射关系,本文定义为磁力密度,分别表示为md1=f1(Fm)、md2=f1(Td),可计算出对应的部件质量。最后,将计算的质量反馈给结构,重新优化设计结构,并重复上述两步,通过反复迭代计算,可优化设计整个磁吸附爬壁机器人。电磁力密度将机器人的结构与动力联系了起来,建立起多学科的统一描述,基于这种描述的优化方法称为统一优化。
统一优化方法建立了爬壁机器人的结构与电磁力的定量关系,有利于机器人的整体优化。多学科知识普遍适用于机器人技术[27-31],爬壁机器人优化设计是典型的多学科的优化问题:机械学科涵盖了静力学分析、结构优化和动力学分析;电磁学科主要涉及磁力密度优化。为了提出统一优化方法,多学科理论具体内容介绍如下:
1.1 结构设计
设计了一款适用于清洁金属面上水泥污垢的磁吸附爬壁机器人,受限于工作空间与电池供电,机器人不但要限制外型尺寸还需要降低重量和驱动功率,整体设计结构如图2所示。
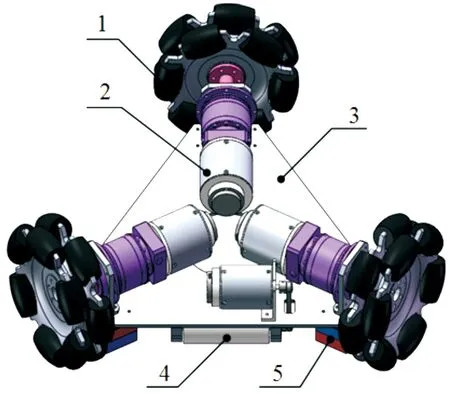
1.全向轮;2.驱动组件;3.底板及连接座;4.清洁模组;5.磁吸附组件
驱动组件由电机和行星减速机组成,直接驱动全向轮;底板及连接座固定各零部件;清洁模组由电机、钢丝刷辊、皮带等组成,通过摩擦墙面清洁污渍。尽管磁轮结合了磁吸附组件及运动轮的特点[32],但轮上只有部分磁铁处于工作状态,导致磁体利用率不足。因此,对称分布于底部的磁吸附组件采用C型结构,可提高永磁体利用率。
为了降低结构质量,需要设计合适的机器人底板结构,其尺寸变量如图3所示。其中a为底板平顶宽度;r为中心圆半径;l为平顶到中心的距离;t为板厚。考虑到平顶宽度及平顶到中心的距离会影响磁力装置的受力和安装,可依据设计条件固化a和l的值简化设计流程,因此机器人结构设计变量可表示为Xs=[r,t]。

图3 底板设计变量图
1.2 静力学分析
考虑到爬壁机器人的使用安全性,机器人非作业状态需要稳定吸附在金属墙面上,应满足2个原则:一是不从墙面滑落;二是在墙面上不发生倾覆。
机器人静止时力学模型如图4所示。图中,Fi和Ni分别表示磁吸附组件受到的吸附力以及轮子受到的支反力(i=1~3);Nc为墙面提供给清洁辊筒的支反力;Ffi为万向轮与墙面间的静摩擦力;Ffc为清洁滚筒与墙面间的静摩擦力;μ1、μ2分别表示全向轮、钢丝刷辊二者与墙面间的摩擦因数;θ为金属墙面倾斜角;G为机器人重力;A点为质心;B点为轮与墙面间的接触点,同时也是倾覆趋势支点。机器人在X、Y轴方向受力平衡,以及绕B点力矩平衡,可列平衡方程:
(1)
(2)
依据磁吸附组件分布特点,可得F1=F2=F3,N2=N3,假设μ1=μ2=μ,联立式(1)和(2)可得:
(3)
(4)
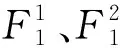
(5)
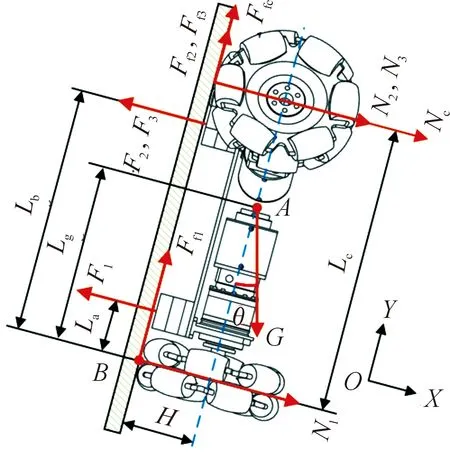
图4 机器人静力学模型图
1.3 动力学分析
机器人在墙面爬行时,除需满足上述2个原则外,还需满足的原则为:电机能驱动全向轮并使得机器人各支点能贴紧墙面。
假定机器人行走时不打滑,当其沿Y轴正向移动,其中一轮在最下方且轮轴线与Y轴平行,此时驱动机器人所需力矩值最大,如图5所示。其中,Ff2,Ff3分别为上端两轮提供的正向摩擦力;Fdc为清洁模组工作时的反向阻力。令R为全向轮半径,依据驱动组件分布特点,有Ff2=Ff3,M1=M2=M3,由动力学模型列平衡方程:
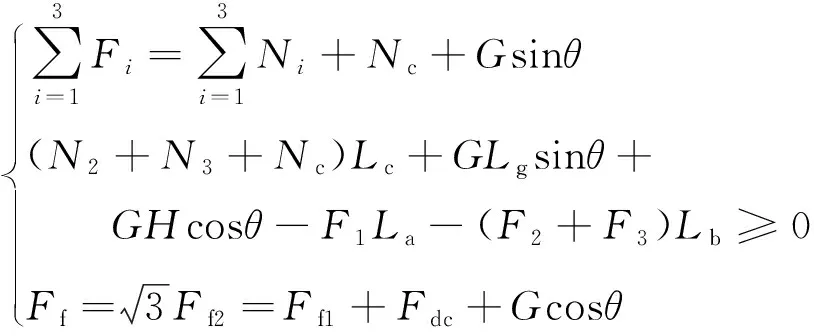
(6)
Ff1=μN1,M2≥Ff2R
(7)
将Fi用Fm替代,联立式(6)和(7),乘以安全系数S2,可得驱动力矩:
(8)
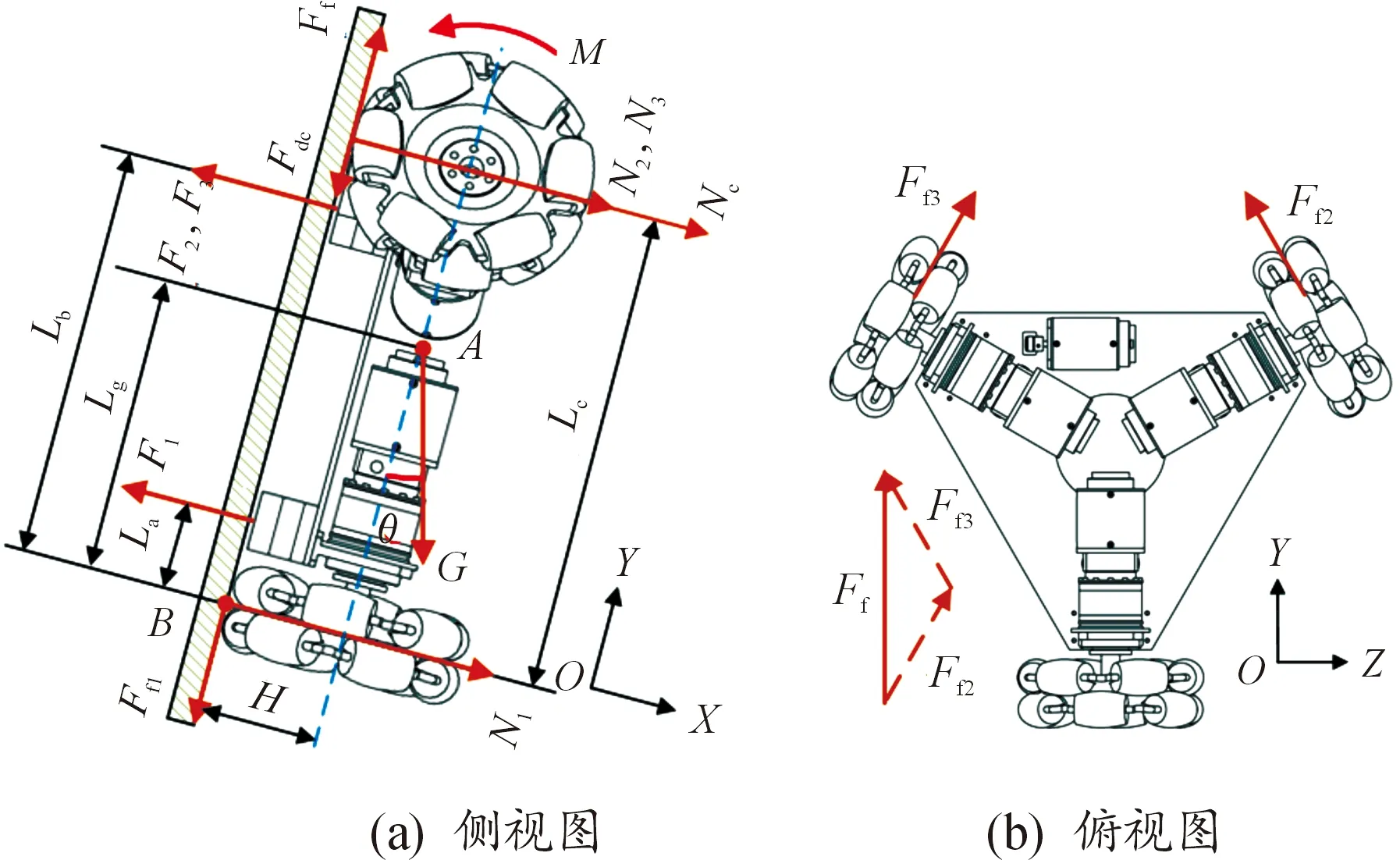
图5 机器人动力学模型图
1.4 磁力密度优化
为了降低磁力装置质量,需要建立磁力装置设计变量与电磁动力之间的联系,以最大磁力密度为条件可以优化磁力装置设计变量。
1.4.1磁吸附力密度优化
磁吸附组件除了提供吸附力,也是机器人质量组成的一部分,结合式(3)—(5)可知,磁吸附组件质量与机器人质量相互影响。为了评估这种影响,定义磁吸附组件的磁力密度为:
ρ1=Fm/md1
(9)
众所周知,对于机器人轻量化设计,磁力密度越大越好。为了计算磁吸附力,可依据电磁特性设计磁吸附组件的结构,其尺寸变量如图6所示。
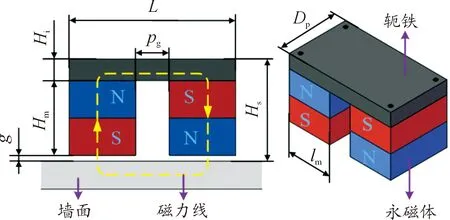
图6 磁吸附组件设计变量图
图6中,g为气隙;L和Hi分别轭铁的长度和厚度;lm和Hm分别为永磁体宽度和高度;Dp为磁吸附组件的深度;Hs为磁吸附组件的顶面与墙面间的距离;Pg为永磁体之间的间隙。由尺寸链可得:
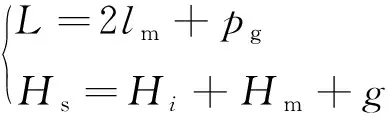
(10)
上式说明磁吸附组件部分变量相互关联,其设计变量可表示为Xd1=[g,Hm,lm,Pg,Dp,Hi]。磁吸附力密度优化可描述为:
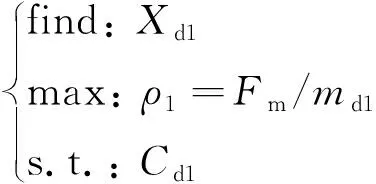
(11)
式中:Cd1为磁吸附组件约束条件。
1.4.2驱动力矩密度优化
驱动组件的设计需要综合考虑减速机的传动比及效率对电机额定设计性能的影响。为了获得高力矩密度,可设计结构紧密的盘式永磁(axial flux permanent magnet,AFPM)电机,包含双转子和铁芯。电机定子通过螺钉固定到壳体上,电机轴一端连接编码器,另一端连接减速机,最后通过联轴器将力矩传递到轮子上。与电机额定力矩Tm相关的表达式为:
Td=ξηrTm
(12)
式中:ξ和ηr分别表示减速机的减速比和效率。同样,为了评估驱动组件质量与机器人质量间的相互影响,定义驱动组件的磁力密度为:
ρ2=Td/md2
(13)
减速机选用标准件,依据其特性并结合式(12)设计电机的结构,如图7所示。其中,导体线径d需按照国标标准线径进行处理,每相绕组匝数N按整数处理;Dmo,Dmi分别表示永磁体的内外径;hm为永磁体厚度;Lc为铁心长度;δ为气隙,考虑安装方便,可取δ=1 mm。因此,电机设计变量可描述为um=[Dmo,Dmi,hm,Lc,d,N]。
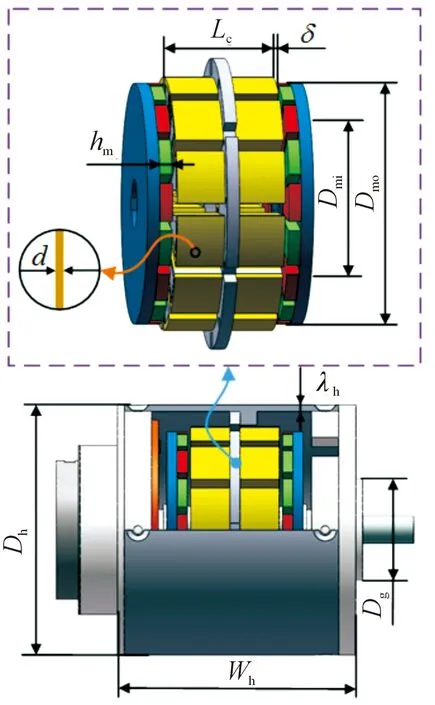
图7 电机设计变量图
电机外壳用于固定电机内部零件以及连接减速机,其结构变量可表示为uh=[Wh,Dh,λh,Dg],其中Wh,Dh,λh,Dg分别表示壳体的长度、直径、厚度以及前端盖与减速机配合的外径。由于uh变量并非独立,与um有关,可表示为uh=F(um),因此驱动组件设计变量可表示为Xd2=[Dmo,Dmi,hm,Lc,d,N]。
驱动力矩密度的优化可描述为:
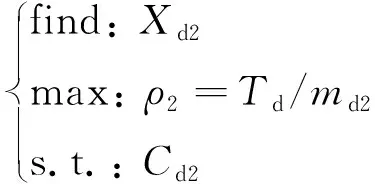
(14)
式中:Cd2为驱动组件约束条件。
电机主轴是电机的主要运动部分,铁心的存在会使得转子受到较大的轴向磁拉力,因此需要校验其强度与刚度。电机结构强度与刚度限制条件Cm可以描述为:
S3σm1≤σy1,S3σm2≤σy2,S3dr≤dlr
(15)
式中:S3为安全系数;σm1,σm2分别为轴和转子的最大等效应力;σy1,σy2分别为轴和转子材料屈服极限;dr,dlr分别为转子的变形量及最大允许变形量。
2 统一优化方法
2.1 约束条件
在整个优化迭代过程中,结构设计变量Xs和电磁动力设计变量Xd会不断更新,因此需要相应的结构约束条件Cs和电磁动力约束条件Cd保证更新的结果仍在约束范围内,其中Cd=[Cd1,Cd2]。依据强度与刚度条件和给定的设计变量范围,结构约束条件Cs的表达式为:
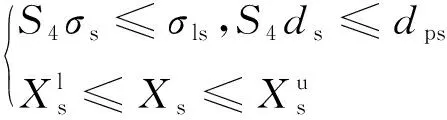
(16)
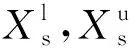
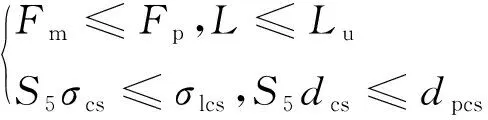
(17)
式中:Fp为磁吸附组件实际提供的吸附力;S5为安全系数;σcs和dcs分别表示轭铁最大的等效应力和变形量;σlcs和dpcs分别为所选材料的屈服极限和允许变形量。对于驱动组件,考虑电机效率ηm以及驱动组件设计变量范围,可得约束条件Cd2:
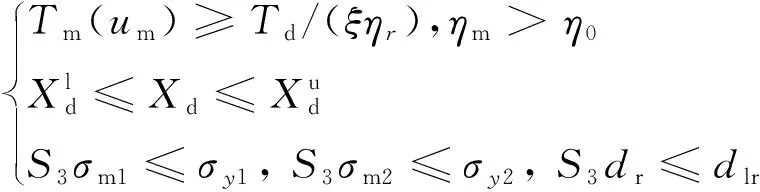
(18)
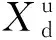
2.2 目标函数
统一优化目的在于满足约束的条件下,减轻机器人重量。目标函数可表示为:
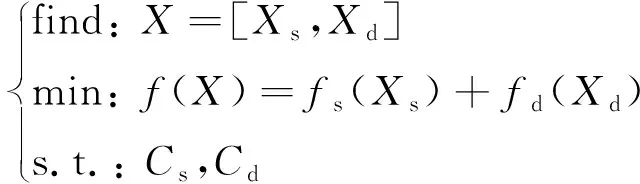
(19)
式中:fs(Xs)、fd(Xs)分别表示结构质量和电磁动力装置质量;X表示全体设计变量。机器人总质量为:
mr=f(X)+mot
(20)
式中:mot为机器人其他部件质量——包括清洁模组、电池、控制器等。
2.3 优化流程
统一优化流程如图8所示。首先,保持电磁动力设计变量固定不变,通过ANSYS内置优化算法搜索最优的局部结构设计变量值。之后,更新机器人质量,保持结构及电磁动力设计变量值不变对机器人进行静力分析,求得所需磁吸附力,并在MAXWELL中进行仿真,得到磁吸附组件设计变量最优值并计算对应质量。最后,将优化得到的变量及质量更新到动力学模型中,获得驱动组件的力矩及电机额定力矩,通过驱动力矩密度优化过程,求取驱动组件设计变量最优值并计算对应质量。比较判断新旧目标函数的差值,直到小于预设值为止,否则进入下一循环。
统一优化过程中,联合MAXWELL优化磁吸附组件的流程如图9所示。将参数化模型导入WORKBENCH,选择MOGA优化模块,设置目标与约束条件,系统自动生成变量值并调用MAXWELL程序进行仿真运算,然后通过有限元分析磁吸附组件强度与刚度,最后进行收敛条件的判断,满足则程序结束,否则进行下一轮迭代。
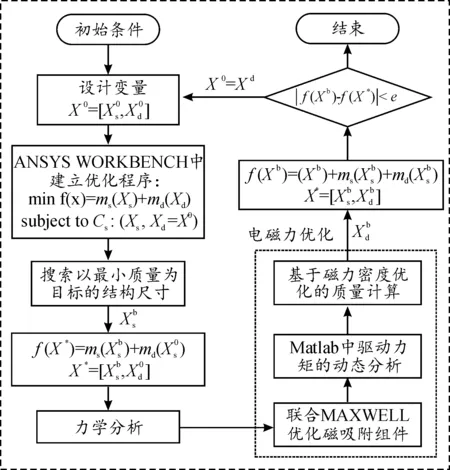
图8 统一优化流程框图
紧随其后的驱动力矩密度优化流程如图10所示,主要应用了复合算法。在Matlab中,程序初始会依据设定生成变量集合,然后通过目标函数进行筛选和排序,并分别标记最好点与最坏点。如果新点的适应性优于最坏点,那么最坏点——目标函数最小点,会被新点替代,否则调整映射操作产生新点。循环过程持续进行,直到最好点和最坏点对应函差值小于给定误差,得到的设计变量值会通过WORKBENCH模型验证电机的结构强度与刚度,直到结果满足条件Cm则程序终止,否则重新生成变量集合。
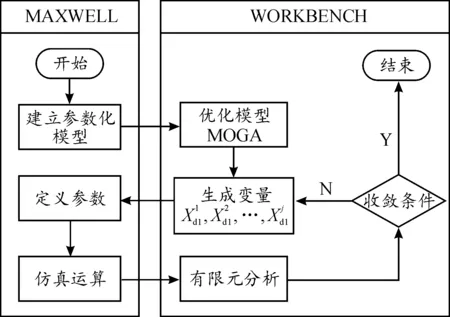
图9 磁吸附力密度优化流程框图
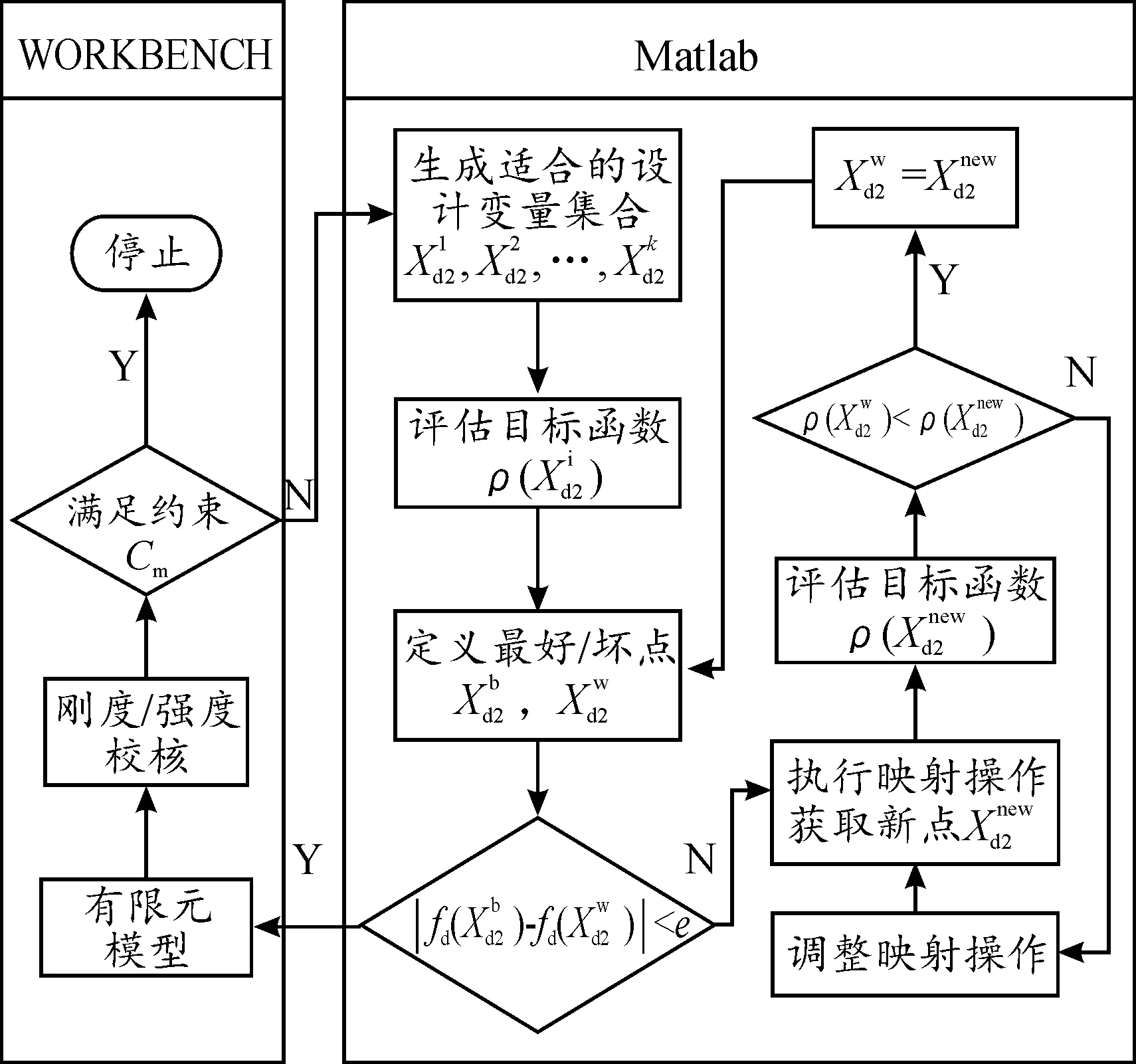
图10 驱动力矩密度优化流程框图
3 实例分析
3.1 参数及初始化
本算例中机器人外形尺寸受工况限制,结构参数表示为:a=90 mm,l=220 mm,La=68 mm,Lb=341 mm,Lc=450 mm,H=102 mm,Lg=250 mm,Lu=100 mm,Hsc=54.6 mm,摩擦因数μ=0.3,安全系数取S1=1.4,S2=1.1,S3=S4=S5=1.2。机器人主体由6061-T6构成,屈服极限σls=270 MPa,设定材料的允许变形量dps=1 mm。全向轮型号为QLM-20,直径为8寸,负载能力为100 kg,额定轮速30 r/min。清洁模组提供的反向摩擦力Fdc=50 N,磁钢材料为N42H,电机主轴和转子材料为45钢,材料的屈服极限σm1=σm2=355 MPa,允许变形量dlr=0.5 mm。
机器人初始质量mr0=30 kg,设计变量的范围及初值如表1所示。联合式(3)和(4)可计算不同倾角下抗滑移和抗倾覆所需的磁吸附力,结果如图11(a)所示;更新质量后,由式(8)可计算不同倾角下的驱动力矩,结果如图11(b)所示。

表1 设计变量的范围及初值
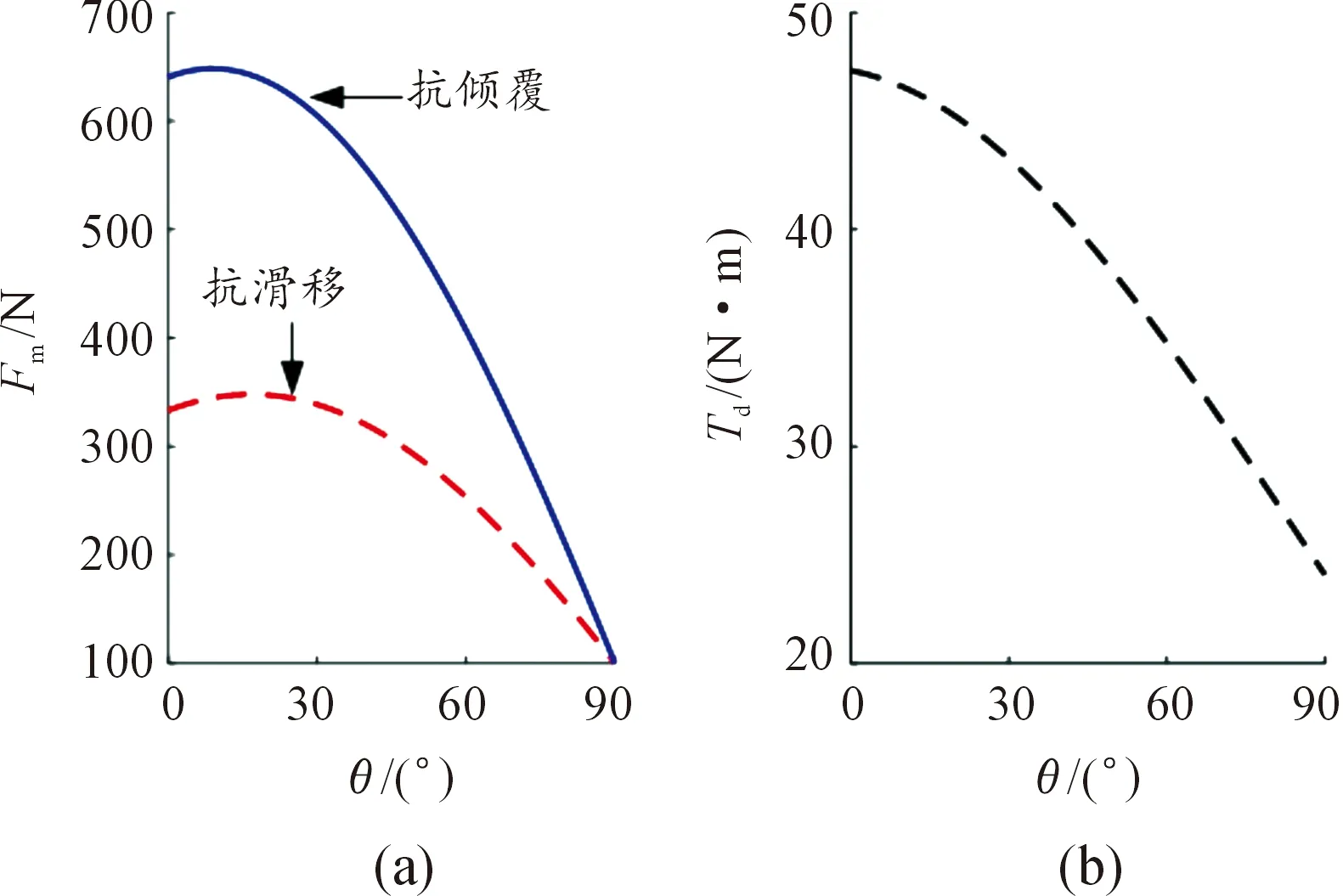
图11 Matlab数字仿真结果
由图11(a)可以看出,墙面倾角为10°时,抵抗倾覆所需磁吸附力为648.6 N;倾角为18°时,防止下滑所需的磁吸附力为348 N。此时,磁吸附组件提供吸附力Fm=908 N,通过式(8)可求出驱动力矩Td=47.5 N·m。
由于PAD系列减速机使用整体式滚珠轴承结构,可以确保刚性及稳定性,而且效率高(ηr≈94%),所以此处选择PAD064-L2行星减速机,其减速比ξ可取4~100范围内的特定值。但是减速比越小,要求电机的额定扭矩会越大,此时可能会导致电机外径过大,超过安装空间。通过评估,最终判定满足设计条件的减速机可选方案有3种,见表2。其中nN为电机额定转速,此时减速机质量为1.5 kg。

表2 电机传动比方案
图12展示了不同方案下驱动的磁力密度优化结果。在A、B、C方案下,驱动的磁力密度最大值分别为15.2、18、20 N·m/kg,可知C方案优于另外2种,因此取ξ=70,此时nN=2 100 r/min。
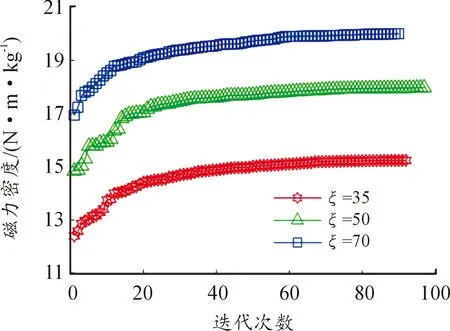
图12 不同方案下驱动的磁力密度优化迭代图
3.2 统一优化结果
依据结构设计变量初值,假设初始Fm=1 kN,进行结构优化,结果如图13所示。在全局优化中,这种局部优化得出的结构尺寸仍有可能是过剩的,统一优化方法是从局部到全局的动态过程,可以确保整体优化方向的正确性。
利用磁吸附力密度优化流程,经过运算处理,结果如图14所示。由驱动组件设计变量初值,结合驱动力矩密度优化流程,可得驱动组件质量收敛结果如图15所示。通过对不同Fm的局部优化,可拟合磁吸附组件的磁力密度曲线;同样,通过对不同Td的局部优化,也可拟合出驱动的磁力密度曲线。磁力密度曲线可以直观反应出设计约束下的电磁动力与磁力装置质量之间的关系,为机器人的全局优化提供了参考方向。通过多点的数据拟合,2种磁力密度曲线结果如图16所示。

图13 底板质量迭代过程
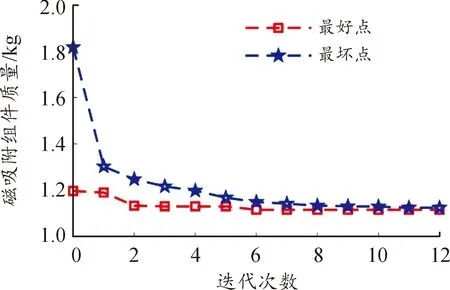
图14 磁吸附组件质量迭代过程
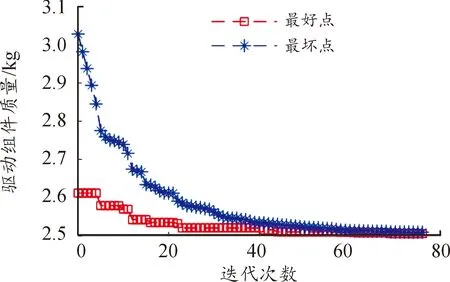
图15 驱动组件质量迭代过程
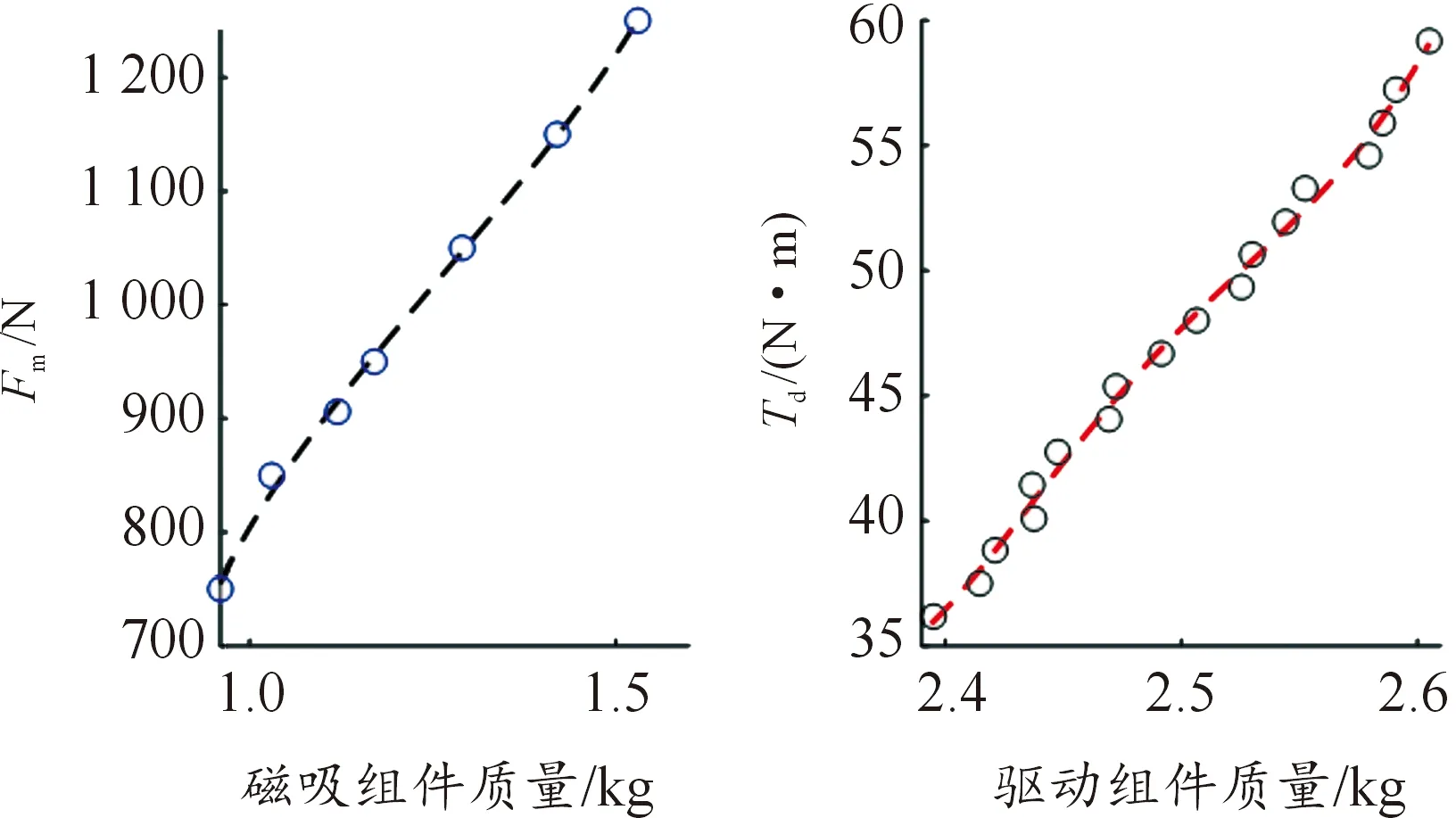
图16 磁力密度
统一优化过程中,机器人整体质量会随着结构、磁吸附组件和驱动组件的局部优化逐渐下降,根据磁力密度曲线的迭代计算,能快速得到机器人质量收敛结果,最终可得设计变量优化值,参见表3。此时,通过计算可求得磁吸附组件的吸附力Fm=768.8 N,驱动力矩Td=40.7 N·m,电机额定力矩Tm=0.62 N·m。
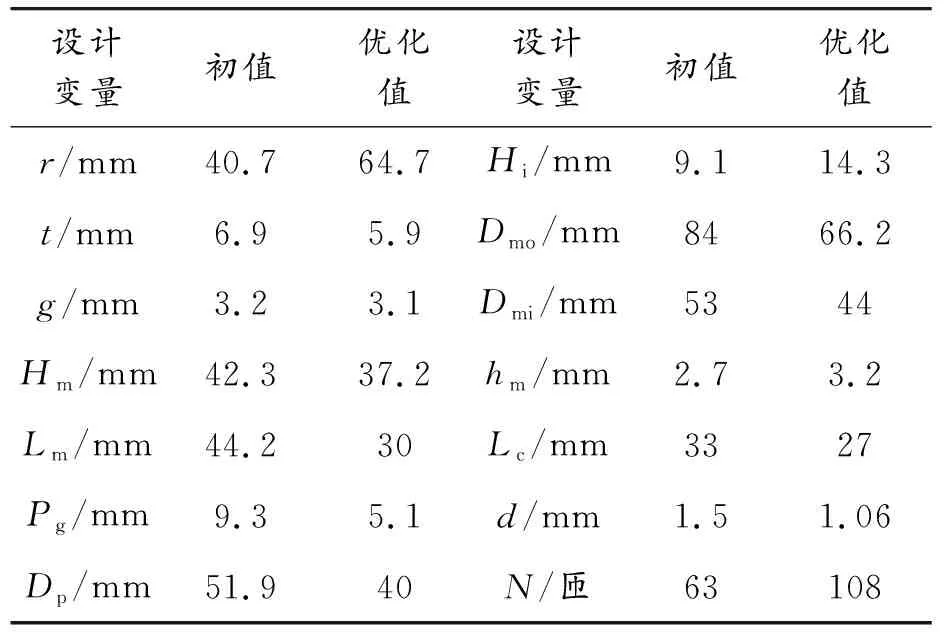
表3 设计变量的初值及优化值
通过统一优化,机器人总体质量迭代的收敛状况如图17所示。可以看出,通过4次优化迭代,机器人质量由初始的30 kg下降到25.4 kg,重量下降15.3%,收敛速度较快。
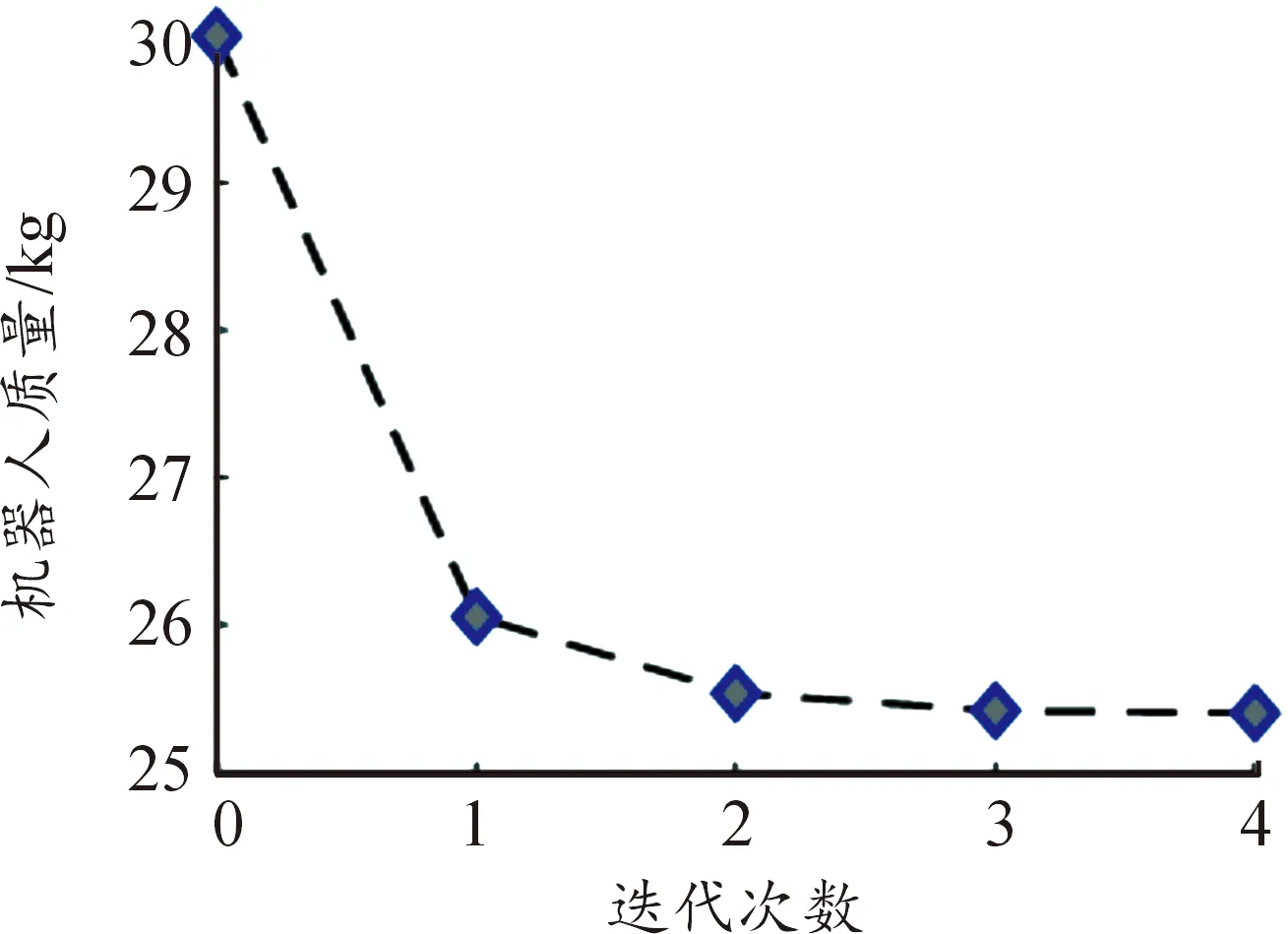
图17 机器人质量迭代图
4 结论
利用电磁力密度的反馈搜寻计算方法减少了很多无序的计算,能够快速有效地优化磁吸附爬壁机器人参数,为机电设备的统一优化设计提供了思路。
