爬壁机器人系统的Noether 对称性和守恒量1)

傅景礼 陆晓丹 项 春

* (山东外事职业大学信息与控制工程学院，山东威海 264504)

† (浙江水利水电学院机械与汽车工程学院，杭州 310018)

** (浙江理工大学数学物理研究所，杭州 310018)

1 引言

柔性机器人可以应用到很多复杂和危险的环境中.关于柔性机器人的研究已经逐渐成为数学、力学、物理学、生物学、材料学等学科的热门研究课题[1-7].

在柔性机器人的研究中,一种爬壁机器人受到关注.21 世纪初期,人们揭示了壁虎能够攀爬在墙面上的原理[8],并掀起了制造爬壁机器人的浪潮.在国际上,爬壁机器人制造原理主要是通过模仿壁虎的运动[9].目前爬壁机器人按移动功能区分主要有吸盘式、车轮式和履带式三种机器人.吸盘式能跨越很小的障碍,但移动速度慢;车轮式移动速度快、控制灵活,但维持一定的吸力较困难;履带式对壁面适应性强,着地面积大,但不易转弯[10].斯坦福大学通过模仿壁虎的行走原理,研发了StickyBot 以及StickyBotⅢ[11]的仿壁虎机器人,模仿的是壁虎自身的行走原理[12-13],该机器人从吸附原理、运动形式都比较接近真实的壁虎.CMU (Carnegie Mellon University)微小型机器人实验室研制了两种结构形式的爬壁机器人[14],即Waalbot 机器人和履带式爬壁机器人,其中Waalbot 机器人是想寻求一种可以借助新的材料,利用粘附原理使爬壁机器人在竖直面上行走;另外一种履带式壁虎机器人,试图找到一种可以粘附在接触面上的材料,使得履带机器人像壁虎一样在墙面上行走.虽然履带式爬壁机器人可以承受较大的负载,但不能实现转弯.加州大学伯克利分校与 iRobot 合作开发了Mecho-Gecko 爬壁机器人,它是两轮驱动的四轮式机器人,通过在足上预装粘合剂和剥离粘合剂来实现对壁面的吸附,其结构相对比较复杂,他们后面又设计了6 腿的爬壁机器人Hexa-Gecko[9].美国克利夫兰大学设计了一种轮腿式爬壁机器人Mini-Whegs[15],这是一种轮式机器人但只能前进不能够后退和转弯等,所以几乎不能够在实际中应用.为了实现各种法向面的灵活过渡,东京工艺研究院和 Isikawajima-Harima 重工业有限公司联合设计开发了“忍者 ”机器人[16],这是一种吸盘式爬壁机器人,该机器人可以很方便地实现前进后退,也可以横向移动,也很容易实现墙面过渡,但是控制的过程特别复杂.

国内在关于爬壁机器人的研究上也做了很多工作.中科院采用模板法已经成功制成了类似壁虎绒毛的微纳米分叉结构[17].上海大学设计开发的采用真空吸附方式和腿足式移动机构,可以适应不同曲率半径的曲面,并可以跨越300 mm 的障碍[18].北京航空航天大学研究的“蓝天洁士”系列是采用真空吸附技术的爬壁清洗机器人[19].南京航空航天大学研制了每个腿具有三个自由度的 IBSS 系列机器人[20-22],但这个机器人质量比较大,载重能力不足,且身体的柔性不足,限制过多.近几年中国科学院合肥物理科学研究院和中国科学技术大学联合提出“抓取+粘附+吸附”的爬壁机器人,相对于先前的爬壁机器人,该机器人可以实现在壁面上稳定的附着同时可以满足在多个壁面上爬行.操纵过程也得到进一步的优化[23-24].

爬壁机器人在进入环境复杂的壁面进行工作时,它的柔性状态尤其重要.要建立柔性爬壁机器人的动力学方程,必须对爬壁机器人的运动形态进行分析.虽然国内外有很多实验室开发研究做出了不同类型的爬壁机器人.但是对于爬壁机器人的动力学研究基本上仅限于牛顿力学方法,由于爬壁机器人结构复杂,约束过多,使得研究十分困难.而基于能量和广义坐标的拉格朗日力学方法对于解决复杂和多约束的问题具有优势.邵洁[25]利用Lagrange 方法建立了爬壁机器人后肢的Lagrange 方程,这个工作显然很不完善.

另一方面,李群理论为求解复杂的微分方程提出了对称性分析方法[26].其中两种基本的Noether对称性方法和Lie 对称性方法已经成为求解复杂工程问题的有效工具[27].众所周知,Noether 对称性方法是基于系统的Hamilton 作用量在变换Lie 群下的不变性给出的一种对称性,来寻找系统存在的守恒量,Noether 对称性方法给出了系统存在的对称性和守恒量(即第一积分,运动常数)之间的一一对应关系.近年来复杂约束力学系统的Noether 对称性理论已趋于完善[28-39],并在物理、连续体,量子力学及诸多工程中得到应用[40-42].

本文拟研究接近于真实壁虎爬行运动的腿式爬壁机器人的Lagrange 方程和Noether 对称性理论.首先,建立爬壁机器人系统的四肢的一个平面简化模型,对爬壁机器人系统引入恰当的广义坐标,并将直角坐标表示为广义坐标的函数,给出爬壁机器人系统的动能和势能从而给出爬壁机器人系统的Lagrange 函数,采用不定乘子法,推导出非完整爬壁机器人系统的Lagrange 方程;其次,引入关于时间和广义坐标的无限小变换,给出爬壁机器人系统Noether 对称性的定义、判据和存在的Noether 守恒量;再者,基于爬壁机器人系统存在的守恒量,给出了该系统的精确解;最后,以在圆锥壁面上爬壁机器人为例,很好地验证了给出的爬壁机器人系统的对称性理论,并进一步给出了该爬壁机器人系统的机身精确解以及四肢的数值解,即得到了该爬壁机器人系统的运动规律.

2 爬壁机器人的动力学分析

爬壁机器人大体上分为履带式,轮式,腿式.其中运动原理最接近壁虎行走过程的是腿式机器人,该机器人是通过模仿壁虎在行走过程中的形态建立起的爬壁机器人模型.本文主要研究腿式机器人,一方面腿式机器人较其他类型机器人的应用范围要广;另一方面,在运动过程中腿式机器人是最贴合壁虎的运动过程的.本文将分析腿式爬壁机器人(如图1所示)的运动.

图1 斯坦福大学的StickyBotIII 机器人Fig.1 StickyBotIII robot at Stanford University

爬壁机器人的运动可以看成是四肢带动身体的一种运动,每条腿上有四个电机驱动,腿部采用杆来连接.该爬壁机器人从运动形式和吸附原理都接近于真实的壁虎.爬壁机器人的工作环境一般是在竖直面,圆柱面以及圆锥面等.本文所讨论的爬壁机器人的工作环境为圆锥壁面,因为圆锥壁面较其他壁面更为复杂,因此只要爬壁机器人可以实现在圆锥壁面上的行走,那么在其余的工作环境也可以行走.

2.1 爬壁机器人四肢运动学

首先计算爬壁机器人在圆锥壁面上四肢相对于身体的坐标和速度.

考虑爬壁机器人的运动,根据爬壁机器人的肢体形态特点,为简化起见,将爬壁机器人四肢各关节看成是一个自由度的转动关节.并将爬壁机器人的单支腿简化为如图2 所示,简化结构由身体0、股骨1、胫骨2 和脚掌3 组成.构件1 和构件0 的连接处为髋关节,构件1 和构件2 的连接处为膝关节,构件2 和构件3 的连接处为踝关节.θ1,θ2,θ3分别为股骨1、胫骨2 和脚掌3 与铅垂线的夹角(规定关节与铅垂线逆时针的夹角为正,顺时针的夹角为负).股骨1、胫骨2 和脚掌3 的质心坐标分别为(x1,y1),(x2,y2),(x3,y3) .令qi=θi(i=1,2,3) 作为广义坐标,并用广义坐标表示直角坐标.

图2 爬壁机器人单腿简化图Fig.2 Simplified view of a single leg of a wall-climbing robot

为简便起见,假设爬壁机器人腿部股骨、胫骨和脚掌长度,质量相等.分别记为 2l和m′.那么,爬壁机器人的股骨相对于身体的质心坐标可用广义坐标表示为

胫骨相对于身体的质心坐标可用广义坐标表示为

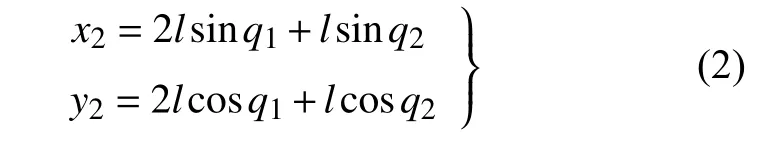
脚掌相对于身体的坐标可用广义坐标表示为

因此股骨相对于身体的速度为

胫骨相对于身体的速度为

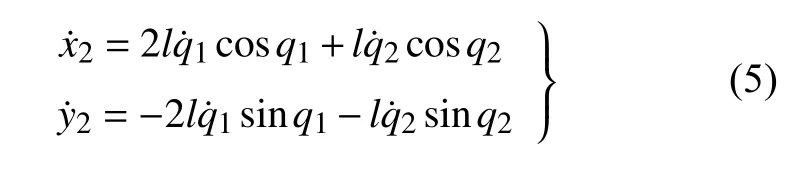
脚掌相对于身体的速度为

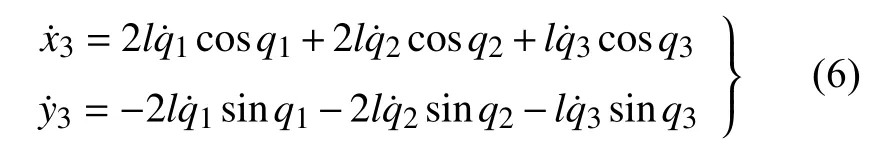
2.2 爬壁机器人机身运动学

接下来研究爬壁机器人在运动过程中机身重心位置坐标以及重心位置的速度变化.爬壁机器人的工作壁面为圆锥曲面,如图3 所示.

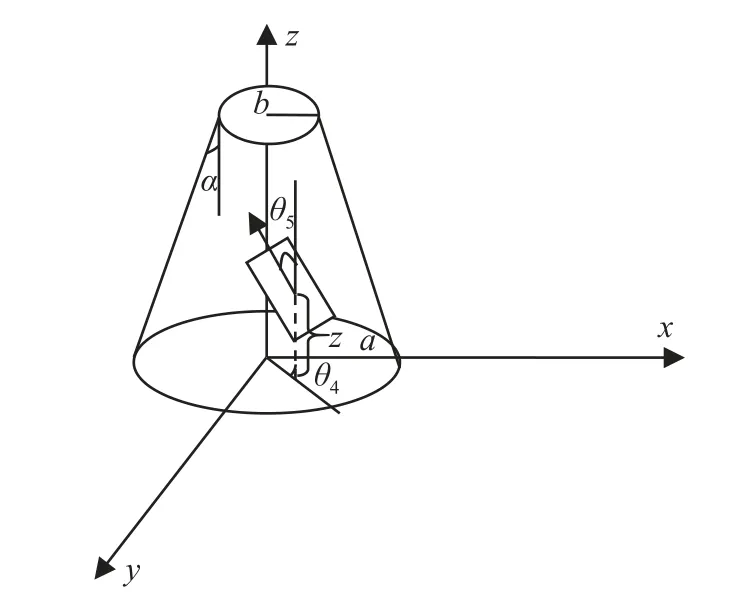
图3 圆锥曲面上的爬壁机器人Fig.3 A wall-climbing robot on a conical surface

在地面中心创建一个固定的笛卡尔坐标系{x,y,z},则在圆锥壁面工作环境下,爬壁机器人的质心位置根据几何学可以表示为

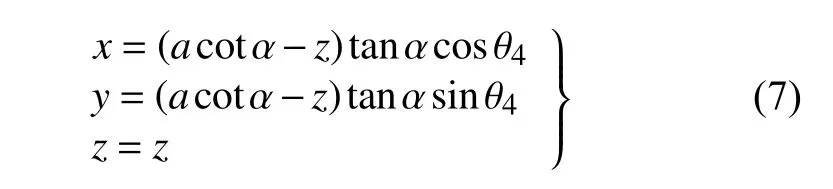
其中,a为圆锥壁面底面圆的半径,b为圆锥壁面顶面圆的半径,h为圆锥壁面的高度,α 为圆锥顶角的一半,θ4为爬壁机器人在底面投影与原点距离的连线与坐标系x轴之间的夹角.其中

选取q4=θ4,q5=θ5,q6=z为爬壁机器人在圆锥壁面上爬行的机身重心广义坐标,其中 θ5为爬壁机器人机身的转动角,则爬壁机器人的机身重心位置的速度为

2.3 爬壁机器人系统动力学分析

通过对壁虎运动的研究发现[33],在攀爬的过程中,壁虎的四条腿并不是同时运动,而是以图4 这种方式向上爬行.

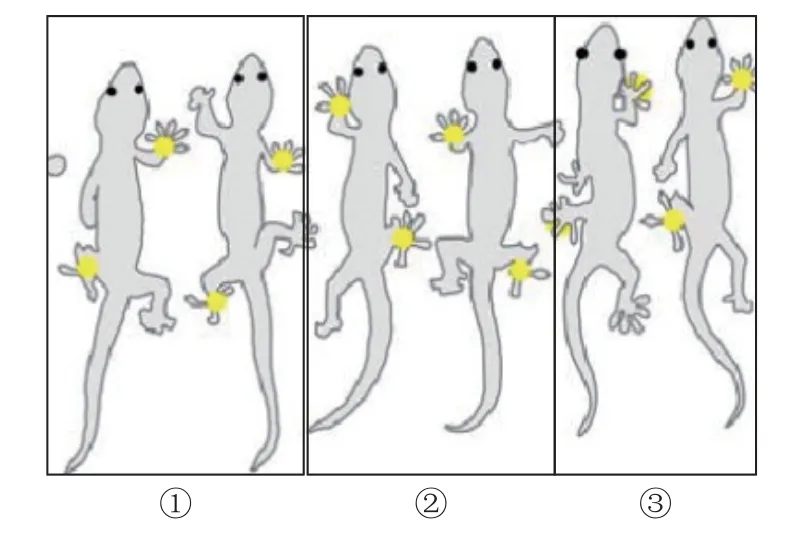
图4 壁虎的爬行运动Fig.4 The creeping movement of a gecko

图中黄色圆点表示脚掌与壁面接触.因为所研究的爬壁机器人系统是建立在壁虎的仿生学基础上,所以对壁虎的运动步态研究就等价于对爬壁机器人系统的步态研究.图2～图4 表明,爬壁机器人系统在攀爬过程中始终有两个脚掌是与壁面接触的,并且在爬行过程中均采用的是对角步态,即左侧前脚与右侧后脚同时运动,右侧前脚与左侧后脚同时运动.同时,通过观察发现,爬壁机器人系统在运动过程中,支撑腿在运动时带动身体运动,同时另外对角两条腿也运动.并且发现,两条支撑腿相对应的各个关节的运动广义坐标角度基本上是相等的.因此为简便起见可将四肢的动能看成是相等的.

设爬壁机器人系统在爬壁中不发生滑动,只存在静摩擦,那么可以得到爬壁机器人的非完整约束条件为

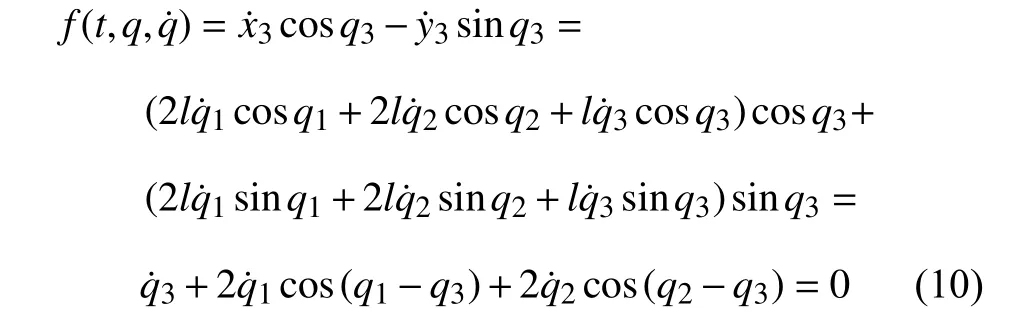
为方便起见,假设爬壁机器人系统在爬壁过程中四肢的动能相同.由此非完整爬壁机器人系统的动能为

其中,T1为非完整爬壁机器人系统相对于身体单条腿的动能,T′为爬壁机器人系统机身的动能,分别为

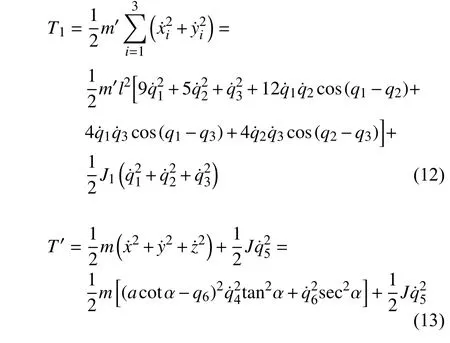
由式(10)可得

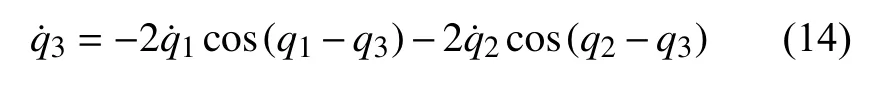
在式(12)和式(13)中,m′为单条腿一关节的质量,m为爬壁机器人系统机身的质量,J为爬壁机器人系统身体的转动惯量,J1为爬壁机器人系统单条腿中关节的转动惯量(本文假设爬壁机器人系统单支腿各个关节的转动惯量相等).

非完整爬壁机器人系统的势能为

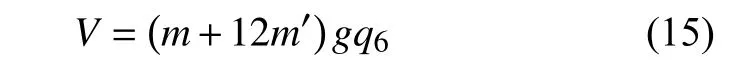
由此非完整爬壁机器人系统的Lagrange 函数为

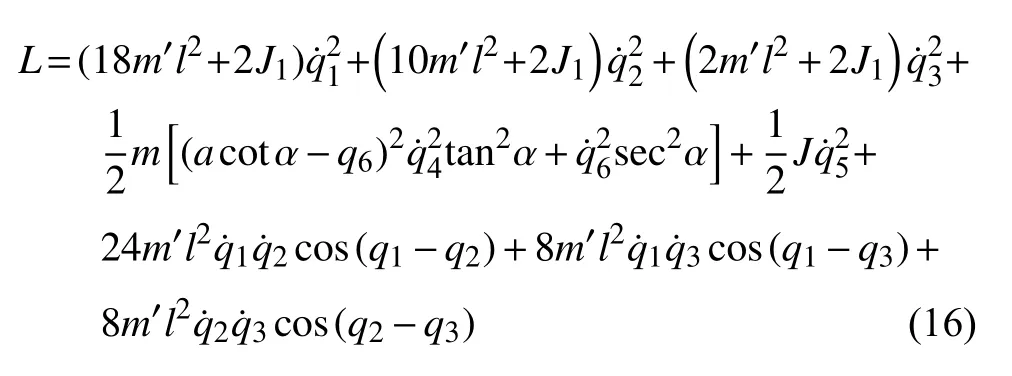
非完整爬壁机器人系统的运动微分方程,即Routh方程为

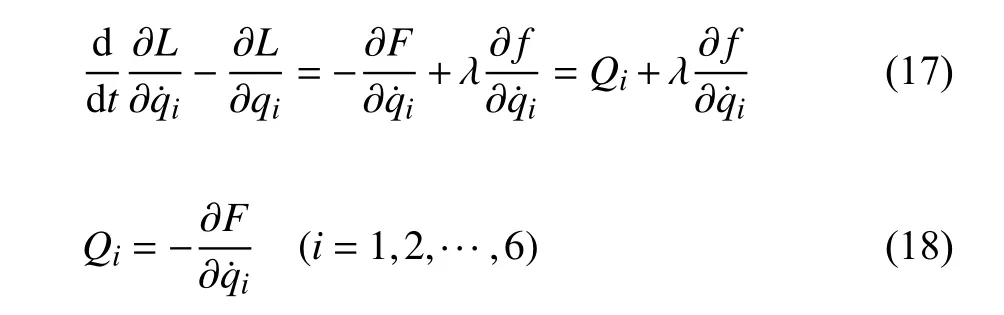
为广义约束反力.方程(20)为非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Lagrange方程.非保守非完整爬壁机器人系统的运动微分方程的解可在方程(20)的解中找到.当爬壁机器人系统在运动过程中满足非完整约束条件(10),则方程(20)的解便可给出非完整爬壁机器人系统(17)的运动规律.

3 爬壁机器人系统的Noether 对称性和Noether 守恒量

引入关于时间和广义坐标的无限小变换

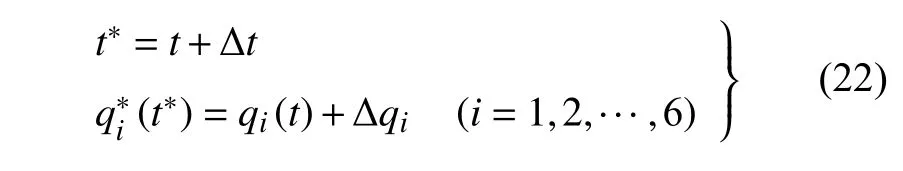
方程(22)可展开为

引入爬壁机器人系统的Hamilton 作用量

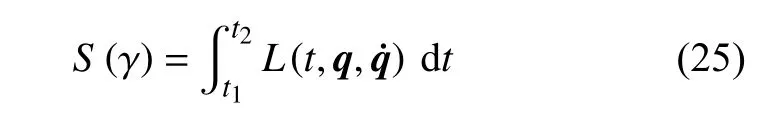
其中,γ 为某曲线,L为爬壁机器人系统的拉格朗日函数,q=(q1,q2,···,q6) .在变换式(23)下,曲线 γ 将变为相靠近的曲线 γ∗,爬壁机器人系统相应的Hamilton作用量变换为

作用量S的变分 ∆S为差S(γ∗)−S(γ) 的相对 ε 的主线性部分,根据全变分和等时变分之间关系,有

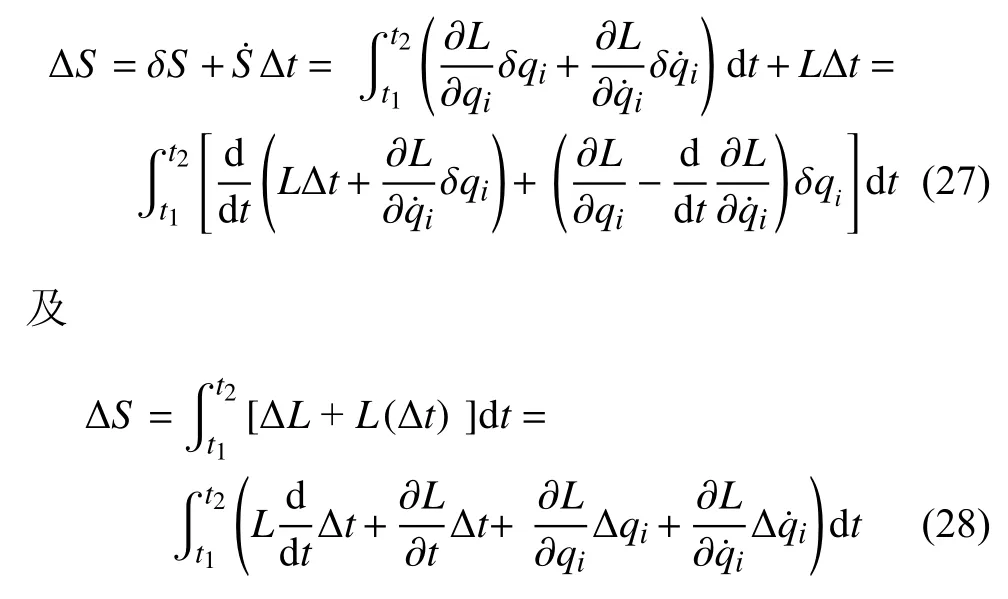
将式(23)代入式(27)并注意到

得到

式(28)和式(30)就是完整爬壁机器人系统的Hamilton 作用量变分的基本公式.

定义1如果爬壁机器人系统的Hamilton 作用量是无限小变换式(22)或式(23)下的不变量,即无限小变换满足

则无限小变换是完整爬壁机器人系统的Noether 对称性变换.

定义2对于受到非势广义力和广义非完整约束力的非保守非完整爬壁机器人系统的Hamilton 作用量是无限小变换式(22)或式(23)下的不变量,即无限小变换满足

由定义公式(31)和基本公式(28)和(30)可以得到完整爬壁机器人系统的如下判据:

判据 1对于无限小群变换式(22),如果满足条件

则变换式(22)是完整爬壁机器人系统的Noether 对称变换.

判据 2对于无限小群变换式(23),如果满足条件

则变换式(23)为完整爬壁机器人系统的Noether 对称变换.

利用关系(24),由于 ε 独立性可以得到完整爬壁机器人系统的Noether 恒等式

Noether 定理1如果无限小变换式(23)是完整爬壁机器人系统的Noether 对称变换,则该系统存在如下形式的守恒量

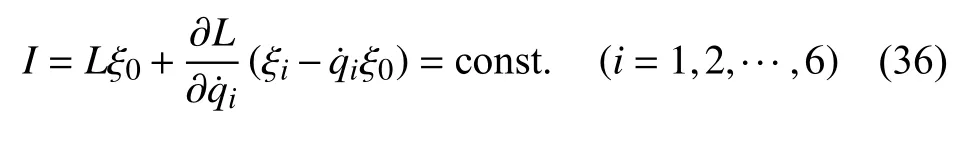
Noether 定理1 也可以表示为Noether 定理2.

Noether 定理2:对于完整爬壁机器人系统,如果无限小变换式(22)或式(23)满足Noether 恒等式(35),则完整爬壁机器人系统存在守恒量(36).

用定义公式(32)及基本公式(28)和(30)可以得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20)广义Noether 准对称性的如下判据:

判据 3对于无限小群变换式(22),如果满足条件

则变换式(22)是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的广义Noether 准对称变换.

判据 4对于无限小群变换式(23),如果满足条件

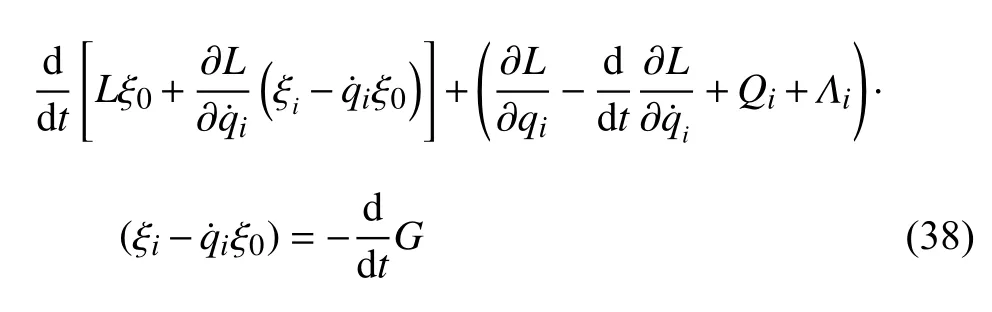
则变换式(23)为非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的广义Noether 准对称变换.

利用关系(24),由于 ε 独立性可以得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20)的Noether 恒等式

Noether 定理3:如果存在规范函数G,使得无限小变换式(23)是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20)的广义Noether 准对称变换,则该系统存在如下形式的守恒量

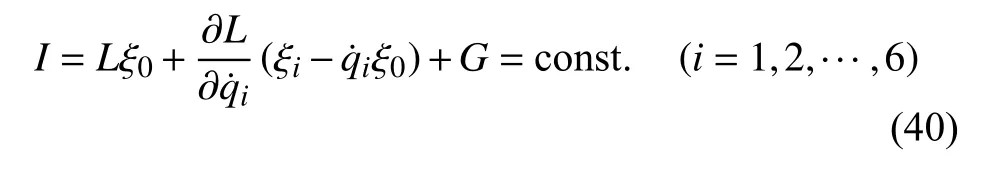
Noether 定理3 可以表示为Noether 定理4.

Noether 定理4:对于非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统(10)和(20),如果存在规范函数G使得无限小变换式(22)或式(23)满足Noether 恒等式(39),则该系统存在守恒量(40).

定义3如果无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的广义Noether 准对称性变换,且变换还满足条件

则称变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的强广义Noether 准对称变换.

Noether 定理5:如果存在规范函数G使得无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的强广义Noether 准对称变换,则该系统存在守恒量(40).

当条件(41)放宽为以下条件

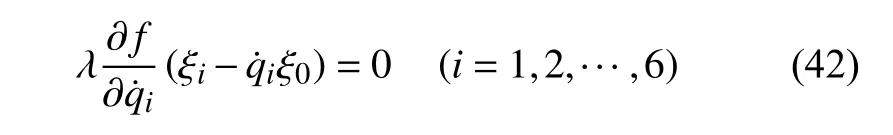
便可以得出非完整爬壁机器人系统(10)和(17)的弱广义Noether 准对称变换.

定义4如果无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的广义Noether 准对称性变换,且变换还满足条件(42)则称变换式(23)为非保守非完整爬壁机器人系统(10)和(17)的弱广义Noehter 准对称变换.

Noether 定理6:如果存在规范函数G使得无限小变换式(23)是非保守非完整爬壁机器人系统(10)和(17)的弱广义Noether 准对称变换,则该系统存在守恒量(40).

由Noether 守恒量(40)再给定初始条件便可得出非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统在圆锥壁面上爬壁过程中的运动规律.

4 利用爬壁机器人系统的Noether 守恒量求其运动规律

在分析力学领域,近30 年来我国梅凤翔教授带领众多学者从事约束力学系统的Noether 对称性和Lie 对称性的研究工作[27,43-59],并提出了约束力学系统的形式不变性(也称梅对称性)理论[60,61],建立了约束力学系统的对称性理论,在国际上产生一定影响.然而在先前的工作中,一般是根据系统的某种对称性给出系统存在的守恒量(第一积分或运动常数),很少进一步由守恒量给出系统的精确解.事实上,当得出第一积分(守恒量,它是一阶微分方程),那么守恒量的求解已经没有困难,对于专门从事于对称性理论研究的人员来说,关于守恒量的求解不需继续进行.然而,近几年来一些学者对此提出异议,并建议将约束力学系统对称性理论应用于多体系统、非线性系统、连续介质系统和工程实际中,因为该方法可为复杂系统提供一个更好的解决思路和方向.下面以复杂的非完整爬壁机器人系统为例,由爬壁机器人系统存在的守恒量,给出爬壁机器人系统的解,即给出爬壁机器人系统的运动规律.

Bluman 对从微分方程的对称性给出特征方程,再得到方程对应的多个第一积分方法进行了系统研究[26].方法表明,如果微分方程的阶数和守恒量的数目相等,便可积分给出微分方程的解.

前面爬壁机器人系统给出的Noether 守恒量都是一阶方程,当给定初始条件时,利用直接积分的方法,便可解出非保守非完整爬壁机器人系统的解,即给出非保守非完整爬壁机器人系统的运动规律.

5 算例

通过以上讨论,已经得出非保守非完整爬壁机器人系统在圆锥壁面上的Lagrane 函数以及非保守非完整爬壁机器人系统的运动微分方程,并给出了爬壁机器人系统的Noether 对称性理论,下面以圆锥壁面上爬壁机器人为例,给出相应的Lagrange 方程,Noether 对称性和Noether 守恒量,Noether 定理,以验证爬壁机器人Noether 对称性理论.并由圆锥壁面上爬壁机器人的守恒量给出精确解,即运动规律.

5.1 圆锥面上爬壁机器人的Lagrange 方程

将式(10),式(16)及式(19)代入到式(17)和式(18)中得

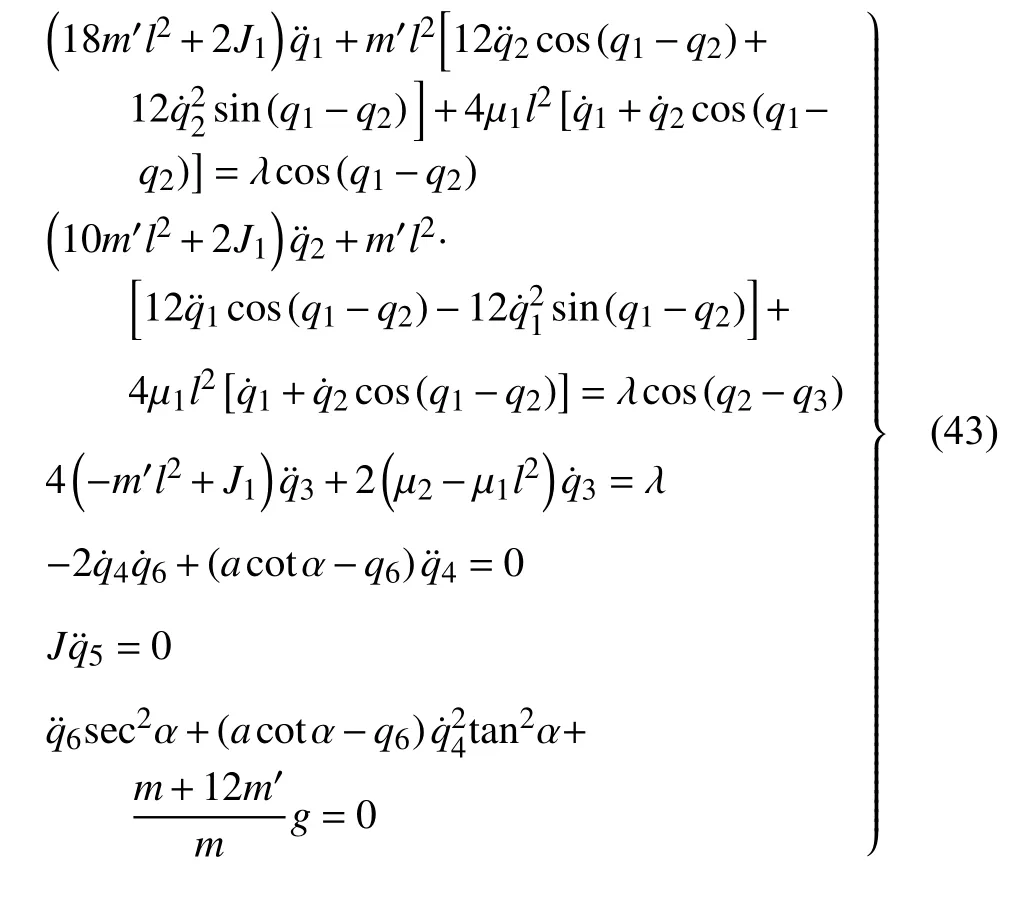
式(43)是非保守非完整爬壁机器人系统在圆锥壁面上的Routh 方程.但如果直接对式(43) 求Lagrang 乘子 λ 是非常复杂的.为了简便起见,现假设在圆锥面上爬壁机器人单支腿任意两个广义坐标中有如下关系

此时非保守非完整爬壁机器人系统在圆锥壁面上的Routh 方程(43)可化简为

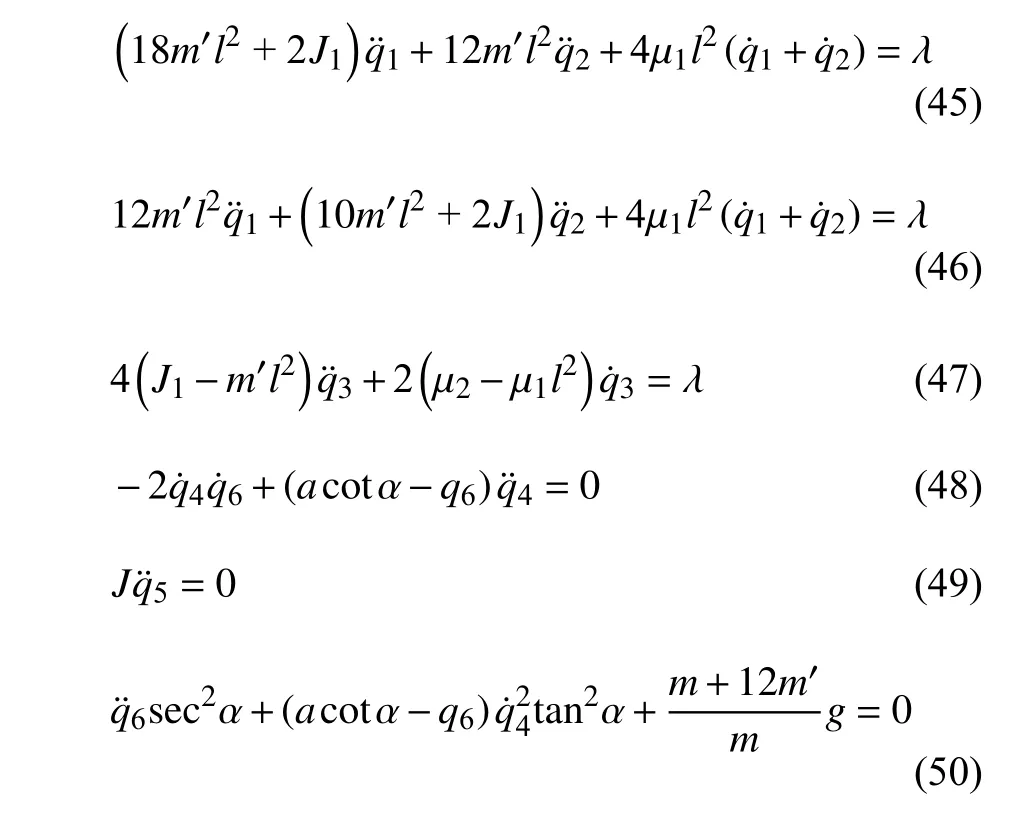
式(45)～ 式(50)便是化简后非保守非完整爬壁机器人系统在圆锥壁面上的Routh 方程.

由式(45)～ 式(47)解出Lagrange 乘子 λ 即

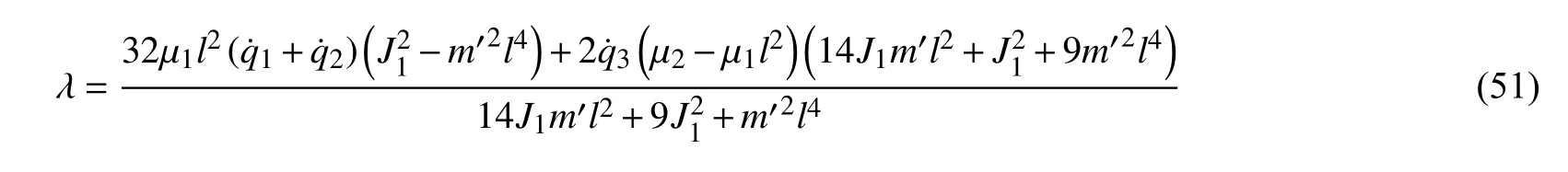
将乘子(51)代入到方程式(45)～ 式(47),即可得到 非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Lagrange 方程

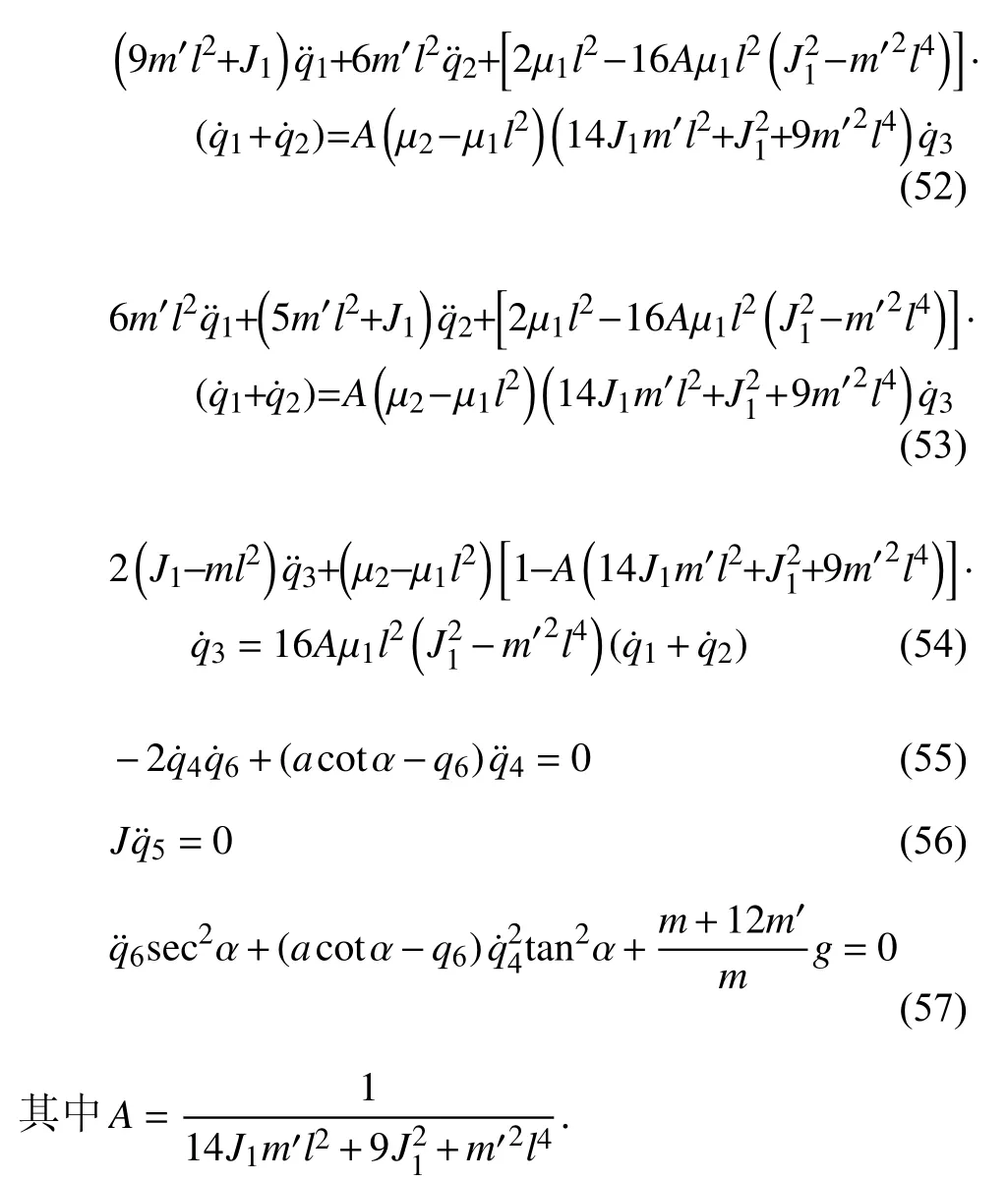
5.2 爬壁机器人的Noether 等式和Noether 守恒量

将式(10)、式(16)、式(19)和式(51)代入式(39),并由假设(44)得到非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Noether 恒等式为

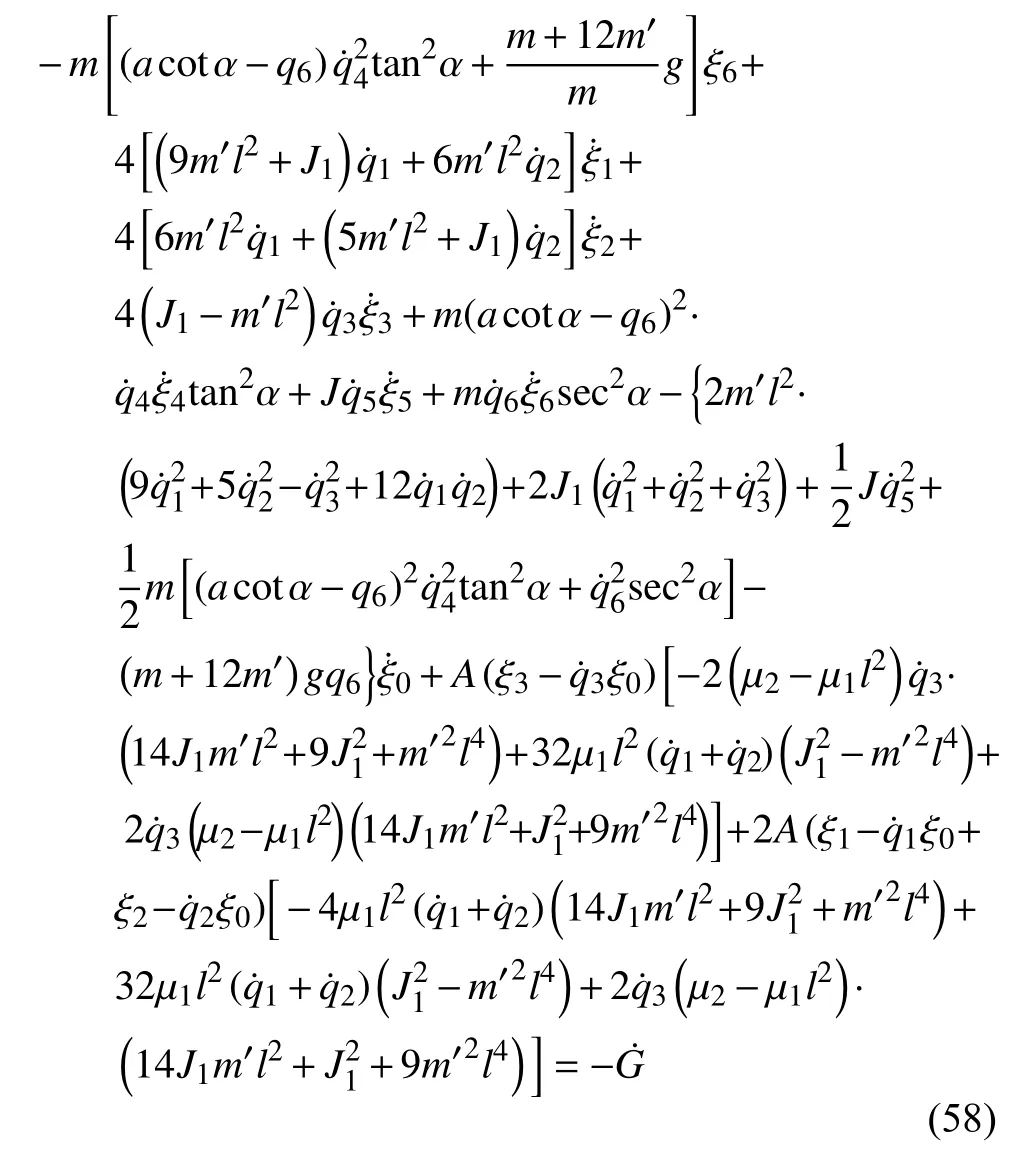
取无限小变换生成元和规范函数为

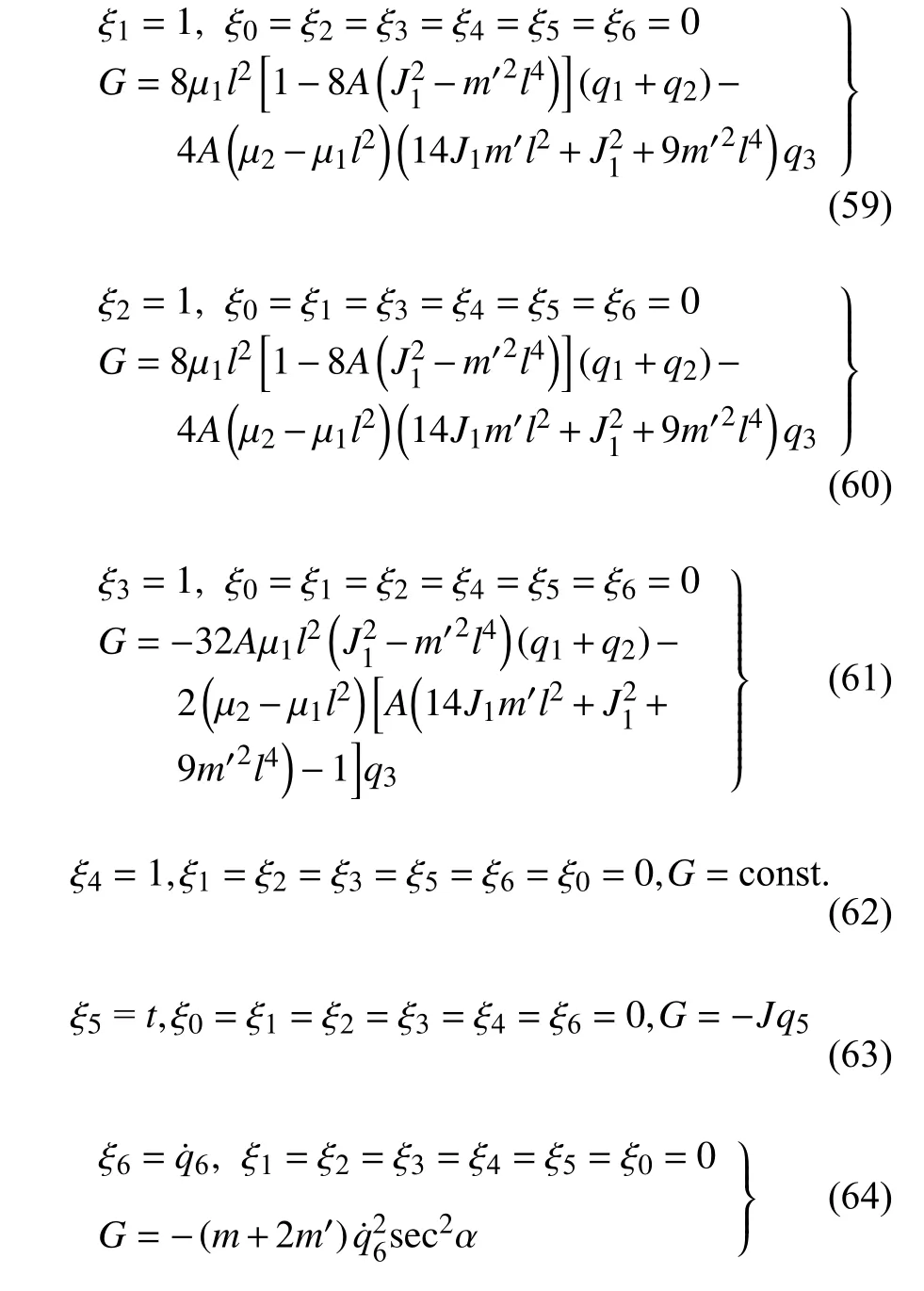
以上得到的生成元和规范函数是对应于非保守非完整爬壁机器人系统相应非保守完整圆锥壁面上爬壁机器人系统的广义准对称变换.

将无限小变换式(59)～ 式(64)分别代入到式(41)和式(42)中.其中无限小变换式(59)～ 式(61)不满足式(41)及式(42),无限小变换式(62)～ 式(64)满足式(41).因此无限小变换式(62)～ 式(64)对应非保守非完整爬壁机器人系统的强广义准对称变换.

对无限小变换式(59)～ 式(61),由Noether 定理3 的守恒量(40)分别给出为

对无限小变换式(62)～ 式(64),由Noether 定理4 的守恒量(40)分别给出为

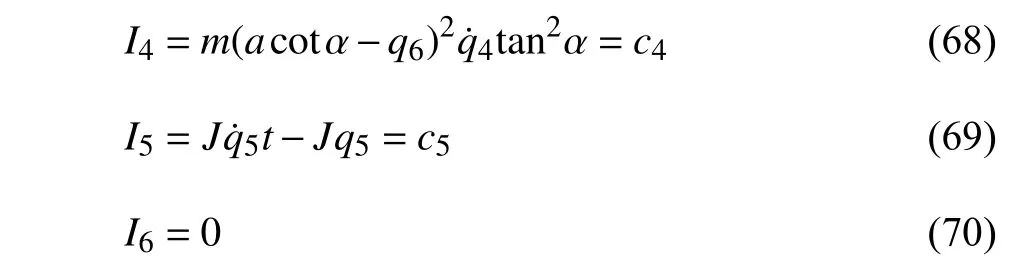
显然,守恒量I6是平庸的.其中守恒量I1,I2,···,I5是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Noether 守恒量.I4,I5是非保守非完整爬壁机器人系统的Noether 守恒量.

下面验证I1,I2,···,I5的守恒性.式(65)对时间求导得

即I1是一个守恒量.

将式(66)对时间求导得

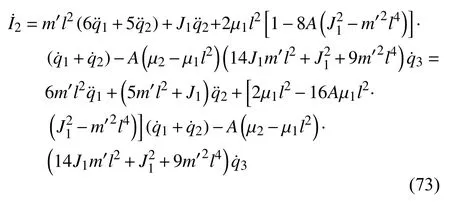
由式(53)得

即I2是一个守恒量.

将式(67)对时间求导得

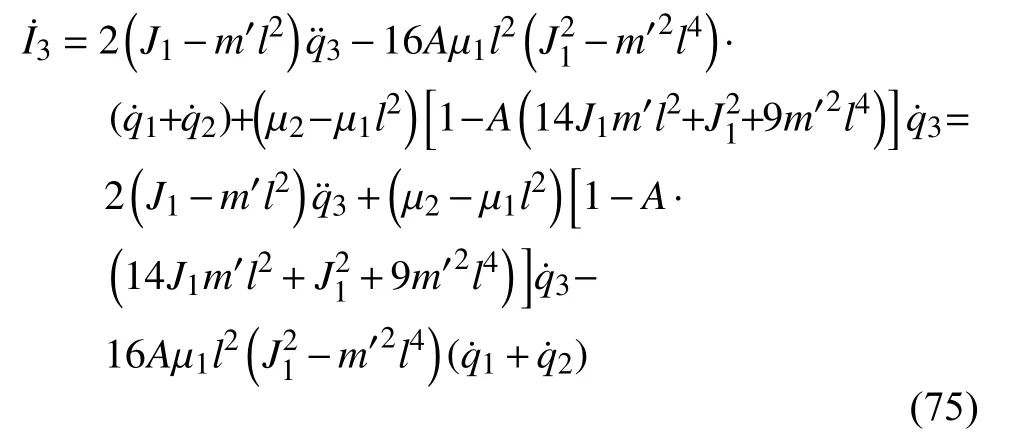
由式(54)得

即I3是一个守恒量.

将式(68)对时间求导得

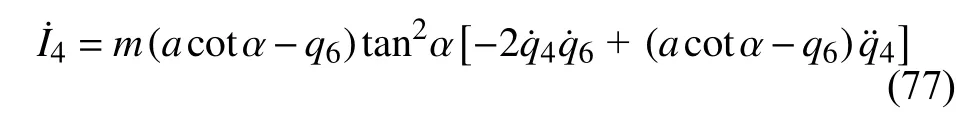
由式(55)得

即I4是一个守恒量.

将式(69)对时间求导得

由式(56)得

即I5是一个守恒量.

可见式(65)～ 式(67)是非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的Noether守恒量.式(68)～ 式(70)是非保守非完整爬壁机器人系统的Noether 守恒量.

5.3 圆锥壁面上爬壁机器人机身的运动规律

利用非保守非完整爬壁机器人的守恒量(68)和(69),可以得出非保守非完整爬壁机器人系统在圆锥壁面上机身的运动规律.

对Noether 守恒量(69)积分可得

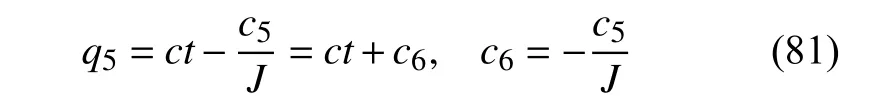
其中,c5为Noether 守恒量(69)的常数,c为不定积分常量.由上式可以看出,爬壁机器人在圆锥壁面上机身的旋转角与时间成正比.

由式(68)得

其中,c4为Noether 守恒量(68)中的常数.将式(82)代入到式(57)中得

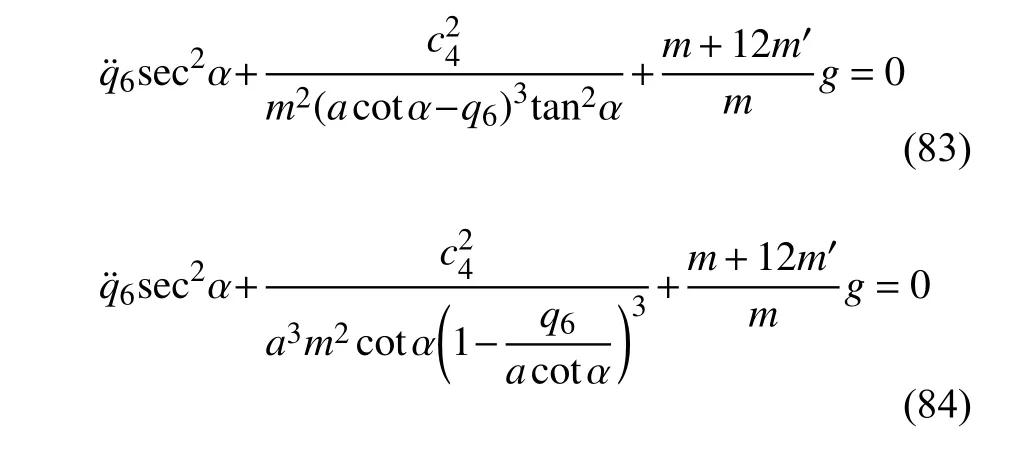
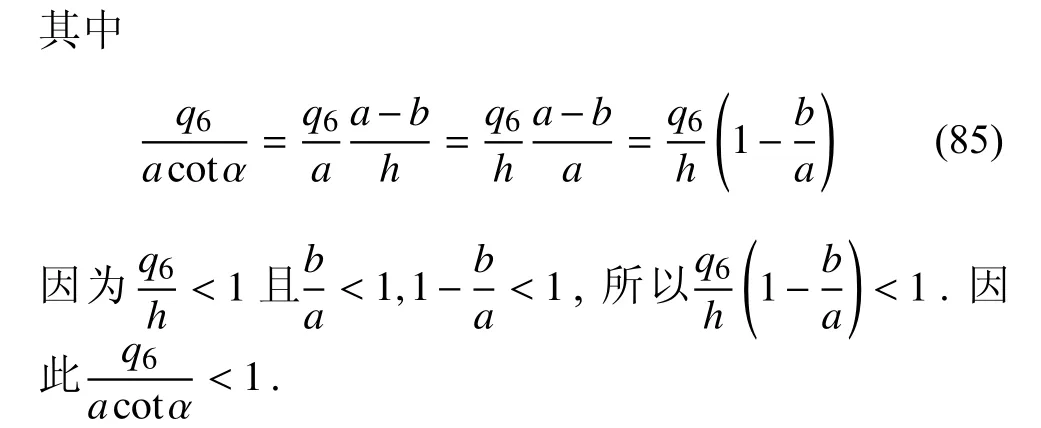
对式(84)利用泰勒公式展开同时精确到一阶无穷小量可以得到

求解式(87)得

假设非保守非完整爬壁机器人在t=0 时以初速度v沿着壁面从底部向上爬行.即t=0 时,q6=0,=vcosα根据初始条件可得

为分析运动规律将式(88)化简得

同样利用泰勒公式展开式(83)得

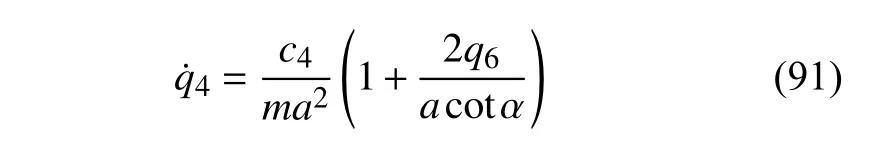
将式(90)代入到式(91)可得

对式(92)积分可得

从式(90)可以看到非保守非完整爬壁机器人在爬壁过程中高度q6和初始速度v,爬壁机器人总体的重量,圆锥壁面的顶角以及底面圆的半径有关.并且该式的周期为,一般情况下,爬壁机器人机身的重量是非常大的,并且圆锥壁面 α 角一般来说比较小,即T是一个非常大的数,不妨假设爬壁机器人在爬壁过程中在T/4 时间内就足以爬到顶峰.这个结论说明,爬壁机器人在爬壁过程中的高度随时间呈非线性递增.

从式(93)可以看出非保守非完整爬壁机器人在爬壁过程中,非保守非完整爬壁机器人在底面投影与原点距离的连线与坐标系x轴之间的夹角q4和时间之间呈非线性关系.

5.4 圆锥壁面上爬壁机器人四肢运动规律

利用非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的守恒量(65)～ (67),便可以得出非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统在圆锥壁面上四肢的运动规律.

为方便研究非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统在圆锥壁面上的四肢运动规律,将爬壁机器人系统四肢的各个关节看成是细直杆.由细直杆的转动惯量[62]可以得知各关节中心位置的转动惯量为

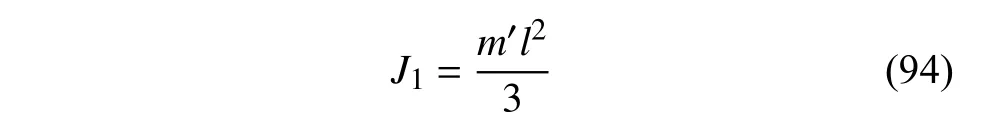
将式(94)代入式(65)～式(67)得

通过查阅相关文献[35],同时考虑到计算的简便可设相应参数的值为

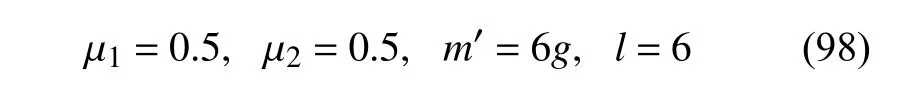
同时假设式(65)～ 式(67)中守恒量的常数为

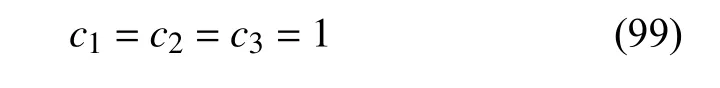
将式(98)和式(99)代入到式(95)～ 式(97)后可得

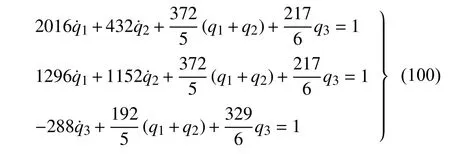
假设初始状态下

可以得到图5 所示的数值解.

图5 四肢各关节运动规律Fig.5 The motion rule of each joint of limbs

通过图5 可以得出在运动过程中随着时间的增加,非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统的股骨,胫骨与铅垂线的夹角q1和q2越来越小并单调递减.这里负值表示爬壁机器人的各关节与铅垂线顺时针方向的夹角.因此单看广义坐标q1和q2夹角的度数来说是先减少后增加,即爬壁机器人在爬壁过程中的股骨和胫骨是左右摆动的.

最后,非保守非完整爬壁机器人系统相应非保守完整爬壁机器人系统中脚掌与铅垂线的夹角呈单调递增.并且通过图像发现,广义坐标q3的夹角的增长速度呈现指数上升的趋势.这也就说明爬壁机器人在爬壁过程中,其脚掌的灵活性要比股骨和胫骨的灵活性高,同时表现出爬壁机器人在爬壁过程中的四肢各个关节中,脚掌的作用力起着重要作用.这也与文献[43]中壁虎四肢的运动规律一致.

6 结论

综合本文的研究,给出如下结论.

(1) 对爬壁机器人这一复杂的动力学系统,本文基于其动能和势能构建了Lagrange 函数,选择恰当的广义坐标,建立了系统的Lagrange 方程;引入Lie 群方法,基于爬壁机器人系统的Hamilton 作用量在变换Lie 群下的不变性,建立了系统的Noether对称性理论,找到了系统存在的一系列守恒量;基于给出的守恒量进行了详细的求解,给出了爬壁机器人系统机身的精确解和四肢的数值解,发现了在圆锥壁面上爬壁机器人的运动规律.

(2) 爬壁机器人是一个多体非完整约束系统,采用的Lagrange 力学方法比牛顿力学方法优势明显,方法简介:首次将Lie 群分析方法用于复杂的爬壁机器人系统,建立了Noether 对称性理论,发现了该系统在运动过程中存在的守恒量,为Lie 群分析方法应用于其他机器人系统奠定了基础;通过利用爬壁机器人系统存在的守恒量,给出了系统的精确解和数值解,为约束力学系统的Noether 对称性理论应用于其他机器人系统展示了美好前景.

(3) 提出爬壁机器人系统的Routh 方程,求出Lagrange 乘子(51),建立了圆锥曲面上爬壁机器人系统的Lagrange 方程(52)～ (57).

(4) 系统建立了爬壁机器人系统的Noether 对称性理论.定义爬壁机器人系统的Hamilton 作用量,给出了Hamilton 作用量的基本变分公式(28)和(30);引入关于爬壁机器人系统的广义坐标和时间的无限小变换(Lie 群变换),基于Hamilton 作用量在变换Lie 群下的不变性,提出了完整爬壁机器人系统的Noether 定理1 和Noether 定理2,在此基础上提出了非保守非完整爬壁机器人系统相应于非保守完整爬壁机器人系统的Noether 定理3 和Noether 定理4,同时提出了非保守非完整爬壁机器人系统的Noether 定理5 和Noether 定理6;基于给出的Noether定理,求出圆锥面上爬壁机器人的Noether 恒等式(58)和一系列对称性的变换Lie 群(59)～ (64);发现了圆锥面上爬壁机器人存在的守恒量I1,I2,···,I6.

(5) 基于给出的守恒量I1,I2,···,I6,给出了圆锥曲面上爬壁机器人机身运动的精确解(81)、(90)和(93)以及四肢在特定参数下运动的数值解(100),即解图5.发现了圆锥曲面上爬壁机器人在爬壁过程中的股骨和胫骨是左右摆动的,其脚掌的灵活性要比股骨和胫骨的灵活性高,同时表现出爬壁机器人在爬壁过程中的四肢各个关节中,脚掌的作用力起着重要作用,这个结论与壁虎爬壁过程中四肢运动规律结论一致.

(6) 研究表明对于一般的爬壁机器人系统的Lagrange 方程存在突出的非线性项,要给出对称性的一般解(精确解)是困难的,只能给出对称性的数值解.

(7) 本文基于爬壁机器人系统的Hamilton 作用量在变换Lie 群下的不变性建立了系统的Noether对称性理论,接下来考虑爬壁机器人系统的Lagrange方程在变换Lie 群下的不变性,建立系统的Lie 对称性理论,并研究在相空间中爬壁机器人系统的Noether 对称性理论和Lie 对称性理论.

(8) 本文给出的方法可以推广应用于其他柔性机器人系统.