参照零模型的符号社会网络嵌入性分析
2022-06-18许小可
李 纪,许小可
(大连民族大学 信息与通信工程学院, 辽宁 大连 116600)
0 引言
在现实世界的很多复杂网络中,节点对之间存在着积极和消极2种关系,如朋友和敌人、合作和对抗、赞成和反对等[1-2]。若将这2种关系抽象为网络连边的符号属性,让正边表示积极关系,负边表示消极关系,这类具有正或负符号连边的特殊网络就被称为符号网络[3-4]。符号网络的相关研究不仅可以为复杂社会系统的网络演化、结构分析和动力学等提供丰富的理论依据,还可以为信息技术领域的个性化推荐、态度预测、用户特征分析等提供实际的应用价值[5]。
在对符号网络的研究中,通常需要考虑负边信息的重要作用,并结合相关统计量来描述网络的结构特征。例如,Kunegis等[6]提出使用节点的正负度之差来描述节点的相对重要性,使用聚类系数来描述网络的凝聚性特征。由于不同的实证网络在规模、类型和结构等方面具有较大差异,很多时候仅仅使用统计量的绝对数值对网络结构特征进行定性或定量分析并不准确[7]。科学严谨的方法是引入该网络随机化后的零模型作为参照对象,基于统计性方法对比分析原始网络和零模型网络相同统计量的相对大小。例如,Maslov等[8]使用零模型作为参照对象研究蛋白质网络拓扑结构的稳定性和特异性,这种研究方法对于符号网络也具有很高的参考价值。
一个与实证网络具有某些相同性质的随机化网络通常被称为该实证网络的随机化副本,这类随机化网络在统计学上又被称为零模型[9-11]。对于符号网络零模型,最常见的是完全随机置乱零模型和符号随机置乱零模型。完全随机置乱零模型是将原网络的连边符号和连边位置都进行随机化置乱,符号随机置乱零模型只是随机化置乱连边符号,连边位置保持不变。以上2种零模型均可在研究符号网络结构特征时作为原始网络的参照,与相关统计量结合就可准确分析出符号网络的非平凡结构特征[12]。
“嵌入性”这一词汇源自经济学,在Granovetter[13]研究经济行为与社会结构之间关系的文章中,对网络嵌入性的概念做了较为全面的阐述。自此以后,嵌入性不论是在经济学领域还是复杂网络领域都得到广泛的重视。在复杂网络领域,针对符号社会网络嵌入性的研究中,结构平衡理论提供了最基本的理论依据[14],像“朋友的朋友是我的朋友”这样的推论已经成为了具有广泛文化认同的格言。Leskovec等[3]利用共同邻居节点数量来衡量节点对之间的嵌入水平,并验证了嵌入水平高的节点对之间更有可能是正边连接,该特性已被广泛用于符号社会网络的符号预测研究中。此外,Yuan等[15]和Wu等[16]都通过设置不同数值的嵌入水平,来检测新提出的符号预测方法的性能。然而,针对大规模在线符号社会网络的嵌入性特征分析结果并不全面,尤其是没有结合零模型进行系统性分析。例如,Leskovec等[3]对符号社会网络的嵌入性进行了初步分析,但其研究只分析了节点对之间的嵌入水平与正边比例之间的关系,没有探讨负边构成对于嵌入水平和网络结构特征的影响。
为了更精确地分析正边拓扑结构、负边拓扑结构、连边符号特征等对网络嵌入性特征的影响,除使用经典的符号随机置乱零模型和完全随机置乱零模型外,又新提出3种更精细化的零模型:正边随机置乱零模型、负边随机置乱零模型和正负边分别随机置乱零模型,共5种零模型作为原始网络的参照对象。结合本文中提出的正嵌入水平检测统计量和负嵌入水平检测统计量,分别对5个实证网络的嵌入性进行分析。实证网络分析结果表明,在符号社会网络中存在:正嵌入水平越强,节点对之间的正边比例越高;负嵌入水平越强,节点对之间的正边比例越低的嵌入性特征。5种零模型分析结果显示,前2种经典零模型的嵌入性特征与原始网络有较大差异,而新提出的3种零模型却与原始网络具有相似的嵌入性特征。表明分别随机化正边或负边拓扑结构,与独立随机化连边符号对符号社会网络的正负嵌入性特征的破坏是不同的。本文结论不仅有助于人们充分理解符号网络嵌入性这类结构特征,还可以在符号预测和链接预测等方面发挥重要作用。
1 实证符号社会网络数据集
本文中共使用了5个实证符号社会网络数据集,分别是Bitcoin-Alpha、Bitcoin-OTC、Wiki-Rfa、Slashdot和Epinions符号网络。其中Bitcoin-Alpha符号网络和Bitcoin-OTC符号网络都来自比特币网上交易平台,前者来自Alpha平台[17],后者来自OTC平台。在交易比特币过程中,交易平台为了防止普通用户在不知情的情况下与劣质用户之间进行交易,进而可能导致普通用户利益受损,Alpha和OTC交易平台都允许用户之间相互标记为朋友和敌人关系,从而可以促成普通用户多与优质用户之间进行交易,并帮助普通用户在交易时尽量躲避劣质用户。
Wiki-Rfa符号网络是一个维基百科管理员投票网络[18]。维基百科在选取管理员时,每一位参与编辑维基百科的用户都可以提出申请,成为维基百科管理员的候选人。后由候选人之间相互投赞成票和反对票,最后通过得票的多少选出新的管理员。Slashdot来自新闻网站Slashdot.com[3],Epinions来自符号网络产品评论者网站Epinions.com[19-20]。这2个网站的用户都可以发表自己的新闻或产品,并允许用户间对各自新闻或产品给出喜欢或讨厌的评价。
表1展示的是上述5个实证符号网络的基本统计数据,包含节点总数、连边总数、正边比例和负边比例。可以发现不同网络的规模有较大差异,具体表现为节点和连边总数从Bitcoin-Alpha网络的几千规模到Epinions网络的几十万规模不等。基于该表也可以发现,所有实证符号社会网络均表现出正边比例远高于负边比例的统计情况。
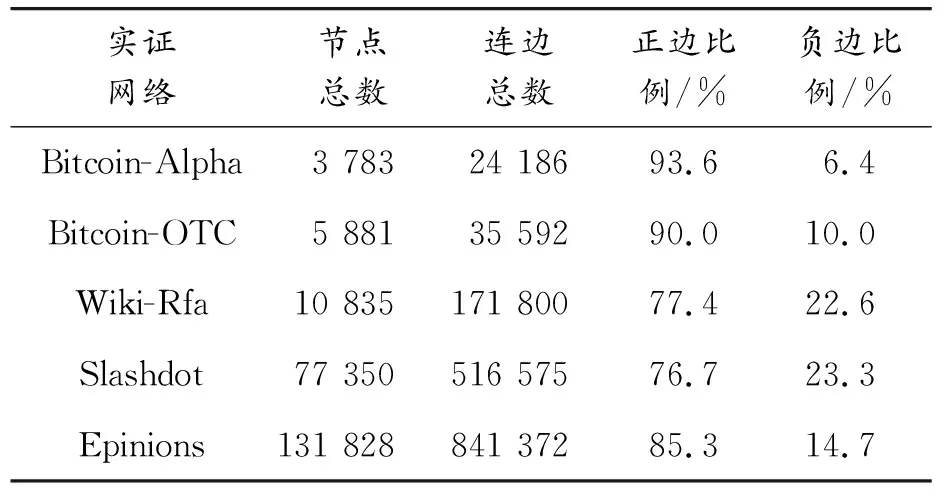
表1 实证符号社会网络基本统计数据
2 符号网络零模型的构造方法
复杂网络零模型的构造方法主要有随机置乱法和网络模型法2种[21]。虽然网络模型法构造的零模型有时可以很好地刻画网络的物理机制[22-23],但是在分析网络内部更深层次的结构特征时,网络模型法很难简洁地构造出零模型作为参照,甚至很有可能无法构造出合适的零模型。随机置乱法与网络模型法的区别是,随机置乱法并不是“从无到有”构造零模型,而是在原始网络的基础上,随机化原始网络的连边位置或某些特定元素,简洁地为原始网络构造出合适的零模型作为参照。为了分析符号网络内部更深层次的结构特征即嵌入性特征,使用的5种符号网络零模型都是基于随机置乱法构造的,分别是符号随机置乱零模型、完全随机置乱零模型、正边随机置乱零模型、负边随机置乱零模型和正负边分别随机置乱零模型。构造方法如图1所示。前2种是在一般符号网络中常用的零模型,后3种是新引入的零模型。
在图1中,(a)表示一个拥有6个节点和7条边的小型原始网络,包含3条正边(BC、DF、EF)和4条负边(AB、AC、CD、DE);(b)表示原始网络随机置乱符号元素后形成的符号随机置乱零模型。
符号随机置乱零模型构造方法:在保持原始网络连边位置不变的基础上,随机选取一条正边和一条负边交换符号。例如将BC和DE交换符号,则BC变为负边,DE变为正边,就可以得到图1(b)所示的符号随机置乱零模型。需要注意,在构造符号随机置乱零模型时,置乱符号仅限正边和负边之间,因为正边与正边、负边与负边之间置乱符号并不会让原始网络产生任何改变。
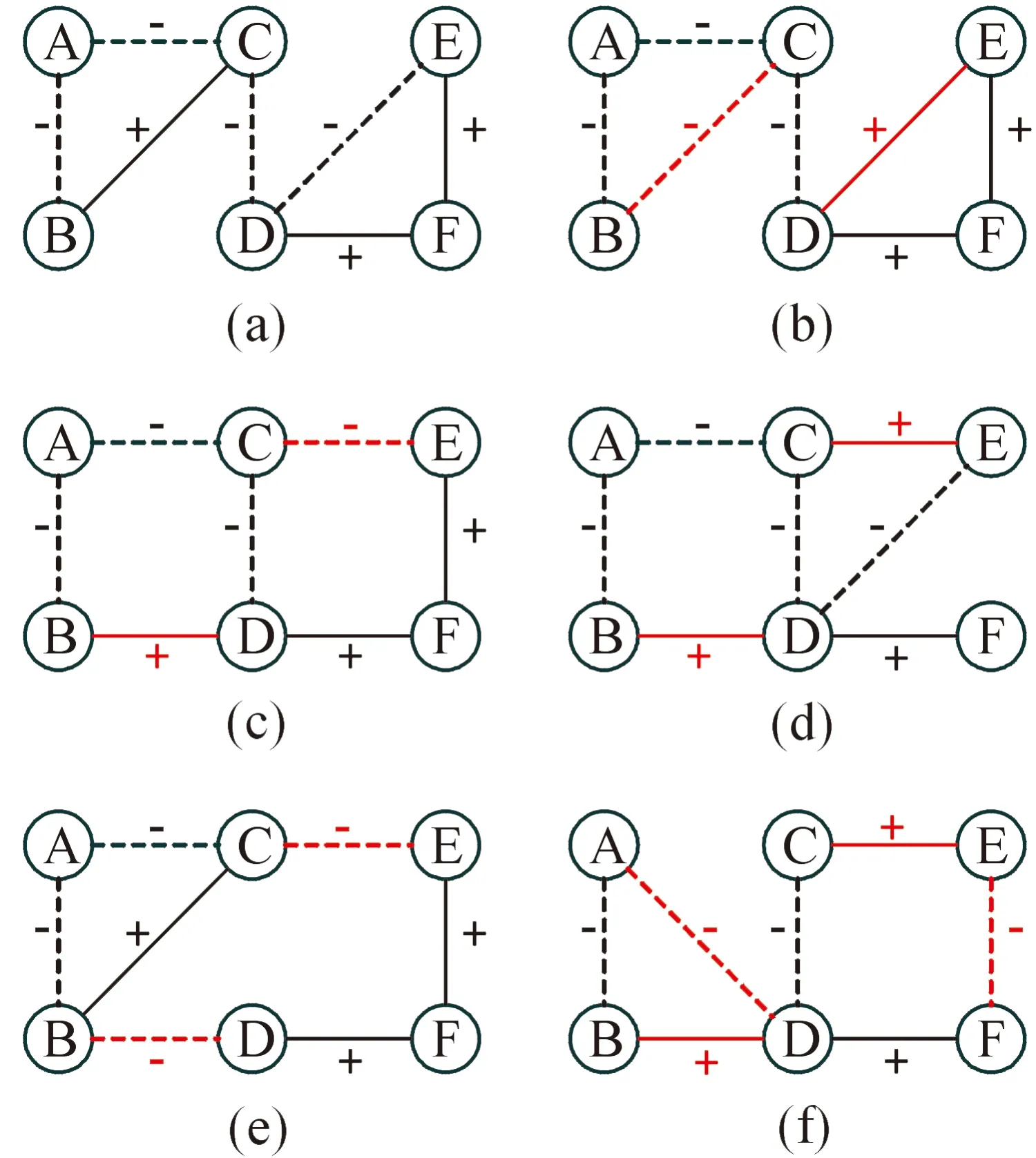
图1 符号网络5种零模型的构造方法
为更详细展示符号随机置乱零模型的构造过程,并将符号随机置乱零模型构造方法运用到其算法中,设计如下伪代码。其中布尔型变量result为成功置乱符号标记,整型变量nswap为成功置乱符号次数,整型变量max_tries为最大尝试置乱符号次数。

符号随机置乱零模型构造算法
输入:原始网络G,置乱次数N;
输出:符号随机置乱零模型。
方法:
result= False;
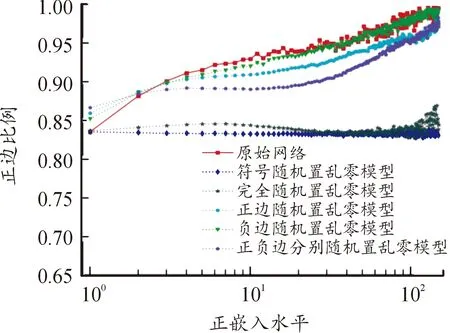
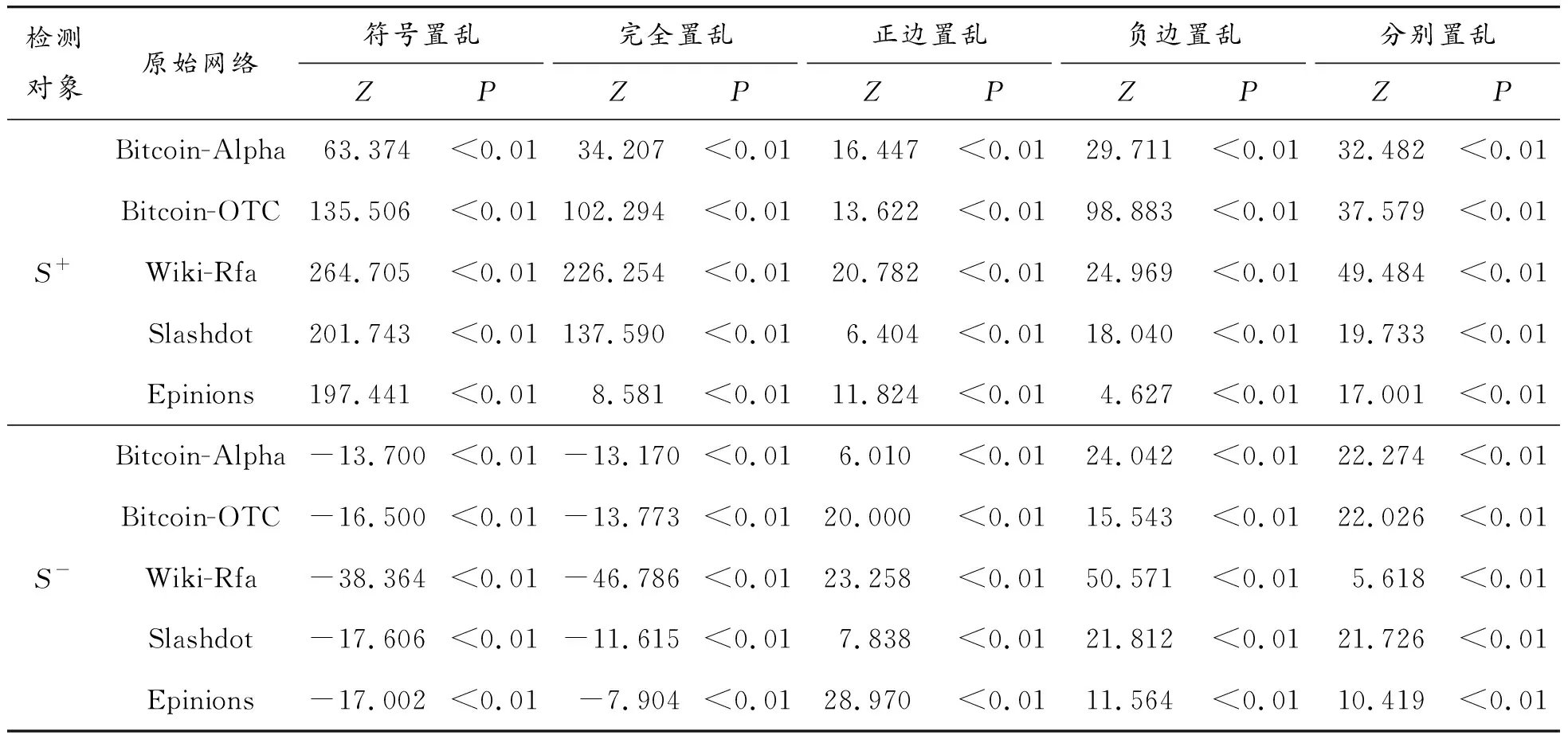
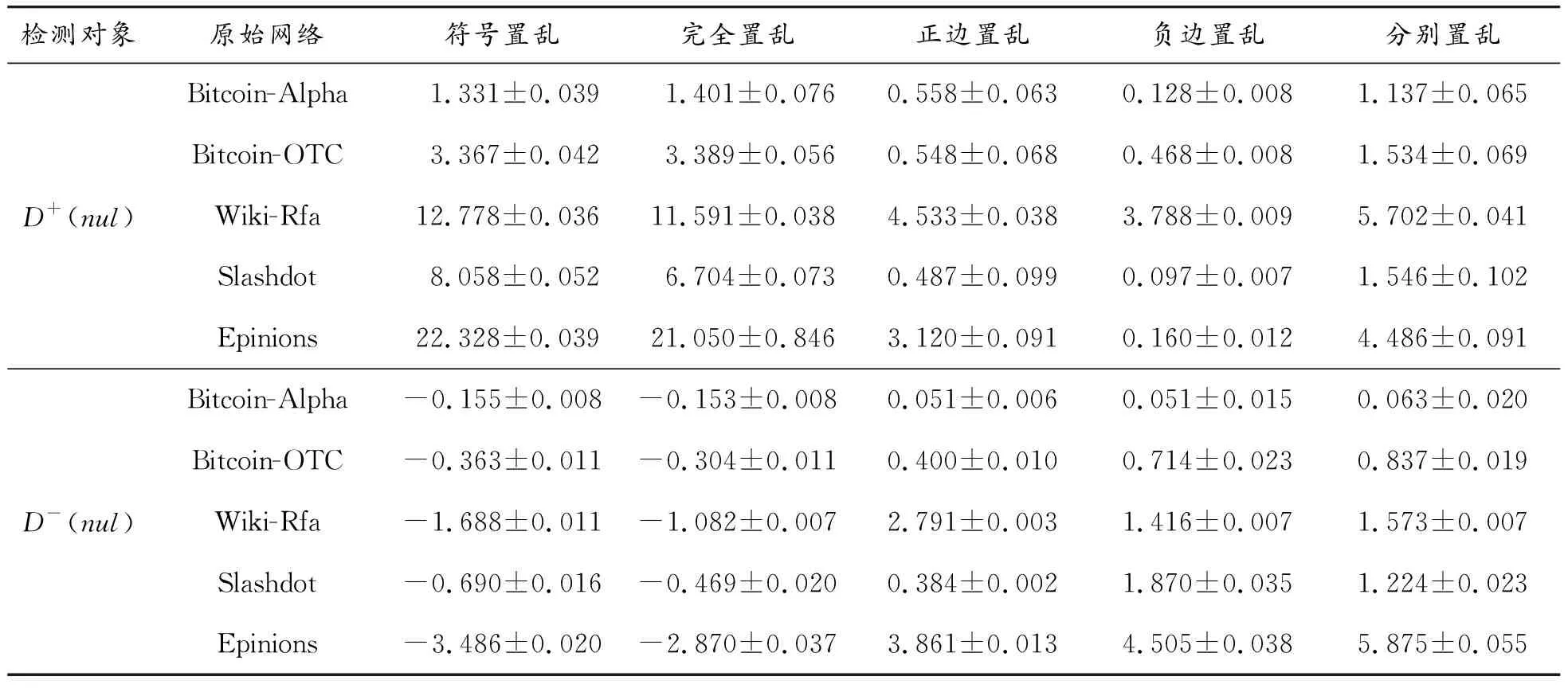
for (nswap= 0,max_tries= 0;nswap { 从G中随机选择2条边em,n和ex,y; if (vm!=vn!=vx!=vy&&(em,n和ex,y的符号不同) ) 交换em,n和ex,y的符号; result= True; nswap++; endif max_tries++; if (max_tries> 5*N) result= False; break; end if } returnG 在图1中,(c)—(f)都表示原始网络随机置乱连边位置后形成的零模型。其中(c)是完全随机置乱零模型、 (d)是正边随机置乱零模型、(e)是负边随机置乱零模型、(f)是正负边分别随机置乱零模型。它们的具体构造方法分别如下。 完全随机置乱零模型构造方法:不考虑连边的正负符号,只是随机选取2条边进行断边重连,并让重连的2条新边和断开的2条原边之间的符号保持不变。例如将BC和DE断开,再重新连接成原始网络中不存在的边BD和CE,并让BC和CE的符号相同,BD和DE的符号相同,就可以得到如图1(c)所示的完全随机置乱零模型。需要注意,由于完全随机置乱零模型并不保证每个节点的正度值和负度值在置乱前后保持不变,因此随机化程度在所有置乱连边位置构造的零模型中是最高的。 正边随机置乱零模型构造方法:保持原始网络的负边连接关系不变,只是随机选取2条正边进行断边重连。例如将BC和EF断开,再重新连接成原始网络中不存在的正边BD和CE,就可以得到如图1(d)所示的正边随机置乱零模型。 负边随机置乱零模型构造方法:保持原始网络的正边连接关系不变,只是随机选取2条负边进行断边重连。例如将CD和DE断开,再重新连接成原始网络中不存在的负边BD和CE,就可以得到如图1(e)所示的负边随机置乱零模型。 正负边分别随机置乱零模型构造方法:若先对原始网络进行正边随机置乱得到正边随机置乱零模型,再对正边随机置乱零模型进行负边随机置乱,就可以得到如图1(f)所示的正负边分别随机置乱零模型。 需要注意,正边随机置乱零模型仅置乱了原始网络的正边拓扑结构,对负边拓扑结构没有影响,因此可以用来分析正边拓扑结构对网络结构特征的影响。同理,负边随机置乱零模型仅置乱了原始网络的负边拓扑结构,对正边拓扑结构没有影响,因此可以用来分析负边拓扑结构对网络结构特征的影响。正负边分别随机置乱零模型在构造过程中,正边只和正边置乱,负边只和负边置乱,并没有进行正负边之间的相互置乱。因此随机化程度弱于完全随机置乱零模型,但要强于正边随机置乱零模型和负边随机置乱零模型。 此外,需要说明的是,在图1所示的零模型构造过程中,所有零模型都只进行了一次随机置乱。若要生成足够随机化的零模型,实际实验中都需要进行足够多次数的重复置乱。在本文中,为了保证所有的零模型都足够随机化,设置的重复置乱次数都是原始网络总边数的5倍以上。 共同邻居是目前最常用的检测网络嵌入水平的统计量。在无符号网络中,共同邻居对于检测网络的嵌入水平有着很好的效果。但在符号网络中,忽略正边和负边的区别,直接使用共同正边邻居作为嵌入水平的检测统计量,会造成负边信息的全部损失。为充分利用符号网络中特有的正边和负边信息,提出将符号网络嵌入水平分为正嵌入水平和负嵌入水平两类。其中正嵌入水平被用来分析正边拓扑结构对符号网络嵌入性的影响,负嵌入水平被用来分析负边拓扑结构对符号网络嵌入性的影响。 为了检测符号网络的正嵌入水平和负嵌入水平,对共同邻居统计量进行改进,分别定义正嵌入水平检测统计量和负嵌入水平检测统计量。2个新统计量的公式为: (1) 在使用上述正嵌入水平检测统计量,分析正边拓扑结构对符号网络嵌入性的影响时,可以绘制以正嵌入水平值为自变量,以该正嵌入水平值下节点对之间的正边比例为因变量的函数曲线。函数公式为: (2) 式中:p+(k)表示正嵌入水平值为k的节点对之间的正边比例;nk表示正嵌入水平值为k的节点对总数;mτ是一个常数,当第τ对节点对之间是正边时,其值为1,否则为0。 同理,在使用负嵌入水平检测统计量分析负边拓扑结构对符号网络嵌入性的影响时,可以绘制以负嵌入水平值为自变量,以该负嵌入水平值下节点对之间的正边比例为因变量的函数曲线。函数公式为: p-(k)=1-p+(k) (3) 式中:p-(k)表示负嵌入水平值为k的节点对之间的正边比例。 使用5种符号网络零模型:符号随机置乱零模型、完全随机置乱零模型、正边随机置乱零模型、负边随机置乱零模型和正负边分别随机置乱零模型,共同作为原始网络的参照对象。结合上文中提出的正嵌入水平检测统计量和负嵌入水平检测统计量,分别研究正边拓扑结构、负边拓扑结构、连边符号特征等对符号网络嵌入性特征的影响。 以Epinions符号网络分析结果为例,其原网络和5种零模型的p+(k)函数曲线如图2所示。从图2可以看出,随着正嵌入水平的变化,节点之间存在连边的比例是最高的,而且随着嵌入性的增强存在连边的比例也在增高。由于符号随机置乱零模型和完全随机置乱零模型中随机化了不同连边的依赖性,节点之间存在连边的比例曲线都近似与X轴平行,说明这2个零模型中的一对节点之间是否存在连边和网络的正嵌入特征是无关的。剩余3种零模型的函数曲线与原网络有着相同的上升趋势,其中又以负边随机置乱零模型的上升趋势与原网络最为接近,但仍略低于原网络。正边随机置乱零模型的上升趋势略低于负边随机置乱零模型,完全随机置乱零模型的上升趋势在这3个零模型中是最低的。同时也需要注意,上述总结的函数曲线变化趋势在较低的正嵌入水平值下并不显著,甚至出现了相关的规律。 图2 Epinions正嵌水平与正边比例关系 不同零模型的函数曲线之所以表现出不同的变化趋势,是由于相对于原网络,5种零模型的随机化程度不同。符号随机置乱零模型和完全随机置乱零模型在生成过程中,均完全打乱了原网络的正边相关性,因此看不出正边拓扑结构对嵌入性的影响。剩余3种零模型,正边随机置乱零模型只是随机化网络的正边拓扑结构,其负边拓扑结构保持不变。负边随机置乱零模型只是随机化网络的负边拓扑结构,其正边拓扑结构保持不变。正负边分别随机置乱零模型只是分别随机化网络的正边拓扑结构和负边拓扑结构,并没有让正边拓扑结构和负边拓扑结构之间进行置乱。因此,剩余3种零模型的随机化程度均低于符号随机置乱零模型和完全随机置乱零模型。在Epinions符号网络中,负边比例又明显低于正边比例,因此负边随机置乱零模型、正边随机置乱零模型和正负边分别随机置乱零模型的随机化程度依次降低,它们的函数曲线上升趋势也依次降低。 与分析正边拓扑结构对符号网络嵌入性的影响类似,同样以Epinions符号网络为例,展现负边拓扑结构对符号网络嵌入性的影响。其原网络和5种零模型的p-(k)函数曲线如图3所示。 从图3可以看出,随着负嵌入水平增强,原始网络的一对节点之间的正边比例降低,说明较强的负嵌入水平损害了节点对之间的正边连接。符号随机置乱零模型和完全随机置乱零模型的函数曲线都近似与X轴平行,再次说明这2个零模型中的一对节点之间是否存在连边和网络的正嵌入特征是无关的。剩余3种零模型的函数曲线与原网络有着相同的下降趋势。但与分析正边拓扑结构对符号网络嵌入性的影响不同的是,这3种零模型的下降趋势均强于原网络,说明这几种零模型对于网络正嵌入性和负嵌入性的影响是不同的。 图3 Epinions负嵌入水平与正边比例关系图 4.3.1量化分析指标 从定性上看,由于Bitcoin-Alpha、Bitcoin-OTC、Wiki-Rfa、Slashdot符号网络的结果和Epinions在图2、图3中的结果是类似的,因此就不再一一展示。为了量化检验上述正边拓扑结构和负边拓扑结构对符号社会网络嵌入性的影响模式,使用原始网络的p+(k)和p-(k)函数值与不同零模型之差作为量化检验指标。2种检验指标的公式为: (4) 式中:D+(nul)指标被用来检验正边拓扑结构对符号网络嵌入性的影响模式;D-(nul)指标被用来检验负边拓扑结构对符号网络嵌入性的影响模式;S+(net)表示原始网络的p+(k)函数与X轴差值累加;S+(nul)表示某种零模型的p+(k)函数与X轴差值累加;S-(net)表示原始网络的p-(k)函数与X轴差值累加;S-(nul)表示某种零模型的p-(k)函数与X轴差值累加。式(4)中S+和S-计算公式都可以表示为: (5) 4.3.2嵌入性特征的统计检验分析 首先引入假设检验方法,分别推断原始网络S+(net)与零模型S+(nul)之间是否有显著性差异、原始网络S-(net)与零模型S-(nul)之间是否有显著性差异。以S+为例(S-检验过程类似,因此不再叙述),可将原假设和备择假设定为: H0:S+(net)=〈S+(nul)〉 H1:S+(net)≠〈S+(nul)〉 式中:〈S+(nul)〉为零模型S+(nul)的均值。可以构造差异检验统计量Z为: (6) 式中:σ+(nul)为零模型S+(nul)的标准差。 假设检验结果如表2所示,可以看出,所有P值均小于0.01,因此可以拒绝原假设H0,接受备择假设H1。在统计学上说明原始网络与5种零模型间的S+和S-均有显著性的差异。为了进一步定量分析原始网络与5种零模型间的差异程度,下面还需要使用D+(nul)和D-(nul)指标来衡量。 分别计算原网络与5种零模型的D+(nul)和D-(nul)指标值,最终结果如表3所示。可见符号随机置乱零模型和完全随机置乱零模型的D+(nul)指标明显大于另外3种零模型。说明符号随机置乱零模型和完全随机置乱零模型的p+(k)函数曲线与原网络的相差较大,另外3种零模型与原网络的相差较小。而在另外3种零模型中,呈现负边随机置乱零模型、正边随机置乱零模型和正负边分别随机置乱零模型的D+(nul)指标值依次升高,说明3种零模型的p+(k)函数曲线与原网络的差异在依次增大。以上数据差异模式与Epinions符号网络中正边拓扑结构对符号网络嵌入性的影响模式相符,从而可以说明,在本文使用的所有数据集中均存在与Epinions符号网络相似的正边嵌入性质。 同时,还可发现符号随机置乱零模型和完全随机置乱零模型的D-(nul)指标呈现负值,而另外3种零模型呈现正值。说明符号随机置乱零模型和完全随机置乱零模型的S-(nul)要大于原网络的S-(net),因此它们的p-(k)函数曲线总体位于原网络之上。新提出的3种零模型的S-(nul)要小于原网络的S-(net),它们的p-(k)函数曲线总体位于原网络的下方。以上差异模式基本与Epinions符号网络中负边拓扑结构对符号网络嵌入性的影响模式相符,说明使用的所有符号网络数据集中,均存在与Epinions符号网络相似的负边嵌入性质,也说明不同的零模型随机化的拓扑结构性质对于网络嵌入性的影响是不同的。 表2 实证符号网络数据集假设检验结果 表3 实证符号网络数据集量化分析结果 通过正嵌入水平下的节点对之间正边比例函数,定性分析正边拓扑结构对符号网络嵌入性的影响,发现正嵌入水平越高的节点对之间正边比例越高;通过负嵌入水平下的节点对之间正边比例函数,定性分析负边拓扑结构对符号网络嵌入性的影响,发现负嵌入水平越高的节点对之间正边比例越低。 符号随机置乱零模型和完全随机置乱零模型的嵌入性特征与原始网络有较大差异,新提出的正边随机置乱零模型、负边随机置乱零模型和正负边分别随机置乱零模型却与原始网络具有相似的嵌入性特征。说明分别随机化正边或负边拓扑结构,与独立随机化连边符号对符号社会网络的正负嵌入性特征的破坏是不同的。 使用零模型作为参照对象分析符号网络嵌入性的方法还可以推广到加权网络、双层网络等其他类型网络中,从而丰富网络结构性质的研究方法库。目前仅给出嵌入性检测统计量来分析符号网络的结构特性,分析角度有限,不足以全面刻画符号网络的结构性质,未来还可以引入更多的统计量,更全面地分析符号网络的结构性质。
3 符号网络嵌入水平统计量
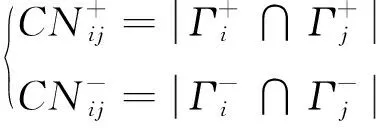
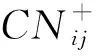

4 参照零模型的符号网络嵌入性分析
4.1 正边拓扑结构对符号网络嵌入性的影响
4.2 负边拓扑结构对符号网络嵌入性的影响

4.3 参照零模型的嵌入性特征量化分析
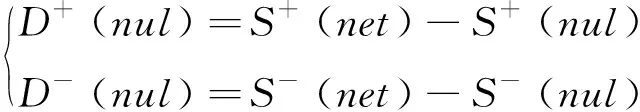

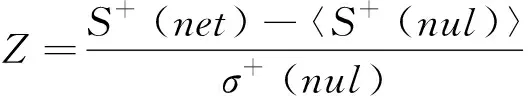
5 结论
