异质多智能体系统预设时间输出二分一致
2022-06-17刘小洋谢春丽
徐 周, 刘小洋, 宋 媚, 谢春丽
(江苏师范大学 计算机科学与技术学院, 江苏 徐州 221116)
0 引言
近年来,多智能体的一致性在工程方面得到广泛应用,受到许多学者的关注[1-2].一致性问题的目标是利用局部信息交互使得所有智能体的状态收敛到相同值.在已有的成果中,许多一致性结果是基于网络节点之间是合作关系这一假设进行讨论的.实际上,节点之间通常既存在合作关系,又存在竞争关系,例如社会关系网络[3],个体之间的关系可能是友好的,也可能是敌对的.基于此,Altafini[4]提出了二分一致的概念,即所有节点的最终状态在数值上达到相同,符号上不同.目前,对多智能体二分一致的研究已经取得一些成果[5-6].但文献中的方法只能实现渐近收敛或者指数收敛,即只有当时间趋于无穷时,系统才能达到二分一致.
在二分一致问题中,收敛速度是一项重要的性能指标.在工程应用中,人们往往希望二分一致可以在有限时间内达到[7-8].然而,多智能体系统的有限时间控制同样具有一定的局限性,其收敛时间依赖于系统的初始值,这严重限制了其适用范围,尤其对于一些大型网络系统.为解决此类问题,Polyakov[9]提出了固定时间控制策略.与有限时间控制方法不同,固定时间控制的收敛时间上界是一个与系统初始条件无关的固定值,然而,它依然不能根据任务需要而提前给定.为此,预设时间控制方法被广泛使用[10-11],如Ren等[10]研究了二阶非线性多智能体系统的预设时间聚类一致;Wang等[11]讨论了多智能体系统的预设时间包含控制问题.
另一方面,在文献[5-8]中,所有的智能体节点都拥有相同的动力学,即同质系统.然而,在实际应用中,智能体常常会拥有不同的动力学行为,甚至不同的维数,因此,异质系统的输出一致被广泛研究[12-15],例如:Hu等[12]基于分布式事件触发策略研究了异质多智能体系统的输出一致问题;Ma等[13]采用自适应的方法在符号网络下讨论了异质多智能体二分输出一致;Zhan等[14-15]通过研究发现,当领导者状态未知时,观测器(或状态补偿器)对于设计异质多智能体输出一致的控制器是必不可少的.虽然关于异质多智能体输出一致的成果已经相当丰富,但很少有研究关注异质多智能体系统预设时间输出一致问题.
因此,本文在文献[14]的基础上,针对网络拓扑为有向图和无向图两种情形,分别讨论异质多智能体的预设时间输出二分一致问题.
1 预备知识与模型描述
1.1 预备知识
定义图G=(W,E,A)为多智能体之间的交互拓扑,其中W={1,2,…,N}表示节点集,E⊆W×W是边集.若G为无向图,则边(i,j)表示节点i和j之间可以相互交换信息.若G为有向图,则边(j,i)表示节点i可以获得节点j的信息.A=(aij)N×N为G的邻接矩阵,其中aij表示边权重值.如果(i,j)∈E,则aij≠0,否则aij=0.本文不考虑节点自环(aii=0)的情况.包含不同节点的一组边序列(ni,ni1),(ni1,ni2),…,(nis,nj)称为路径.如果图G中任意两个不同节点都可以被一条路径所连接,则称图G为强连通图.
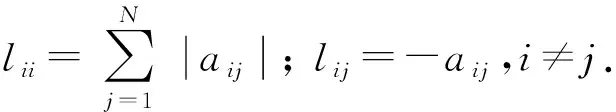
记矩阵B=diag(b1,b2,…,bN),其中bi>0表示第i个跟随者可以直接获得领导者的信息,否则bi=0.记矩阵M=(mij)N×N=L+B.
引理1[4]如果图G为结构平衡图,则存在一个对角矩阵D=diag(d1,d2,…,dN),di∈{1,-1},使得矩阵DAD的所有元素非负.
注1由引理1可知,矩阵DMD是正定矩阵.又因为矩阵M相似于DMD,所以矩阵M也是正定矩阵.进一步,存在对角矩阵Π=diag(π1,π2,…,πN)>0,使得ΠM+MTΠ>0.
1.2 模型描述
考虑一类异质线性多智能体系统,其领导者的动力学方程为
(1)
第i个跟随者的动力学方程为
(2)
其中:x0∈Rn0,xi∈Rni,y0∈Rl,yi∈Rl分别表示领导者和第i个跟随者的状态和输出;ui∈Rmi表示第i个跟随者的控制输入;A0∈Rn0×n0,Ai∈Rni×ni,C0∈Rl×n0,Bi∈Rni×mi,Ci∈Rl×ni;i∈W.
假设1A0的特征值不含有正实部.
假设2方程组
存在解(Φi,Ui),i∈W.
假设3矩阵对(Ai,Bi)可稳定,i∈W.
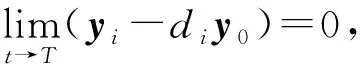
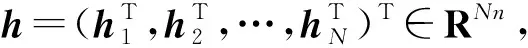
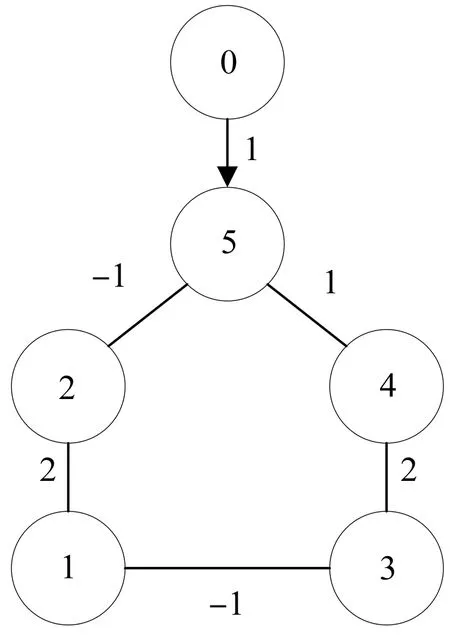
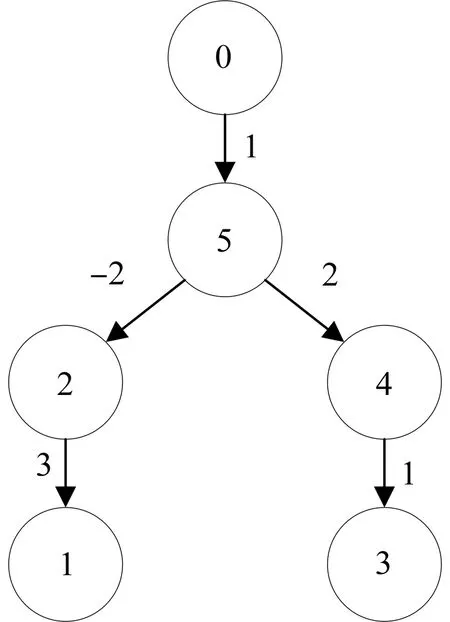
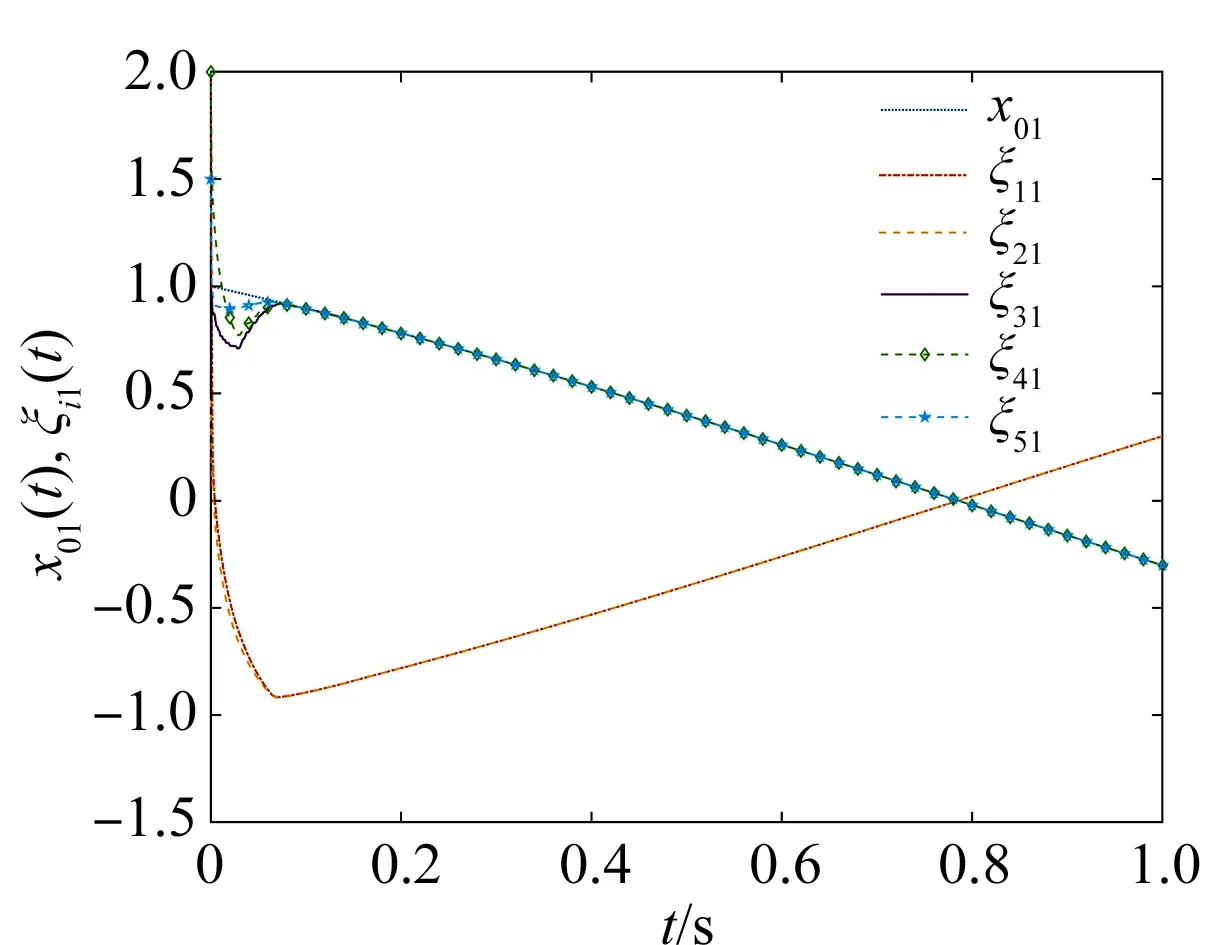
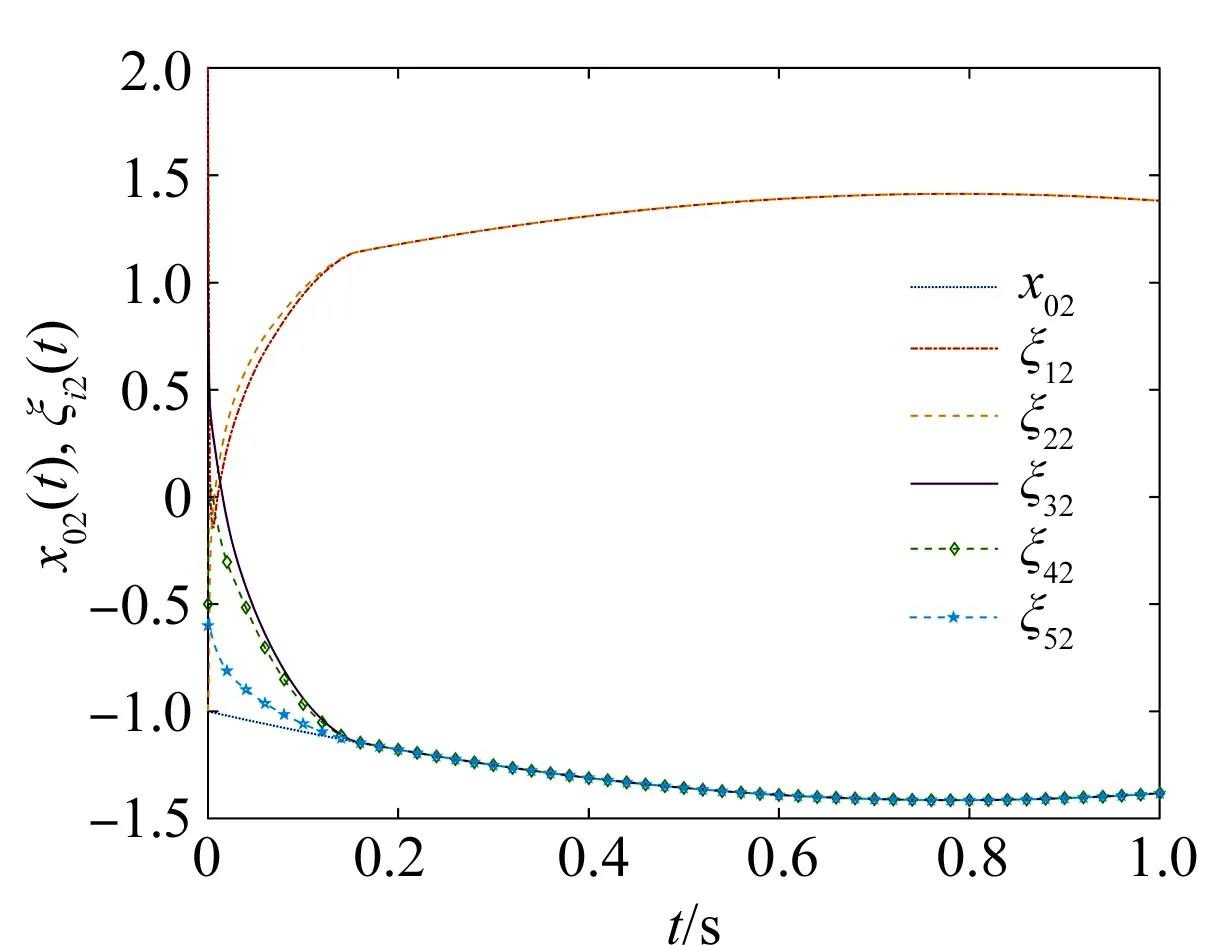
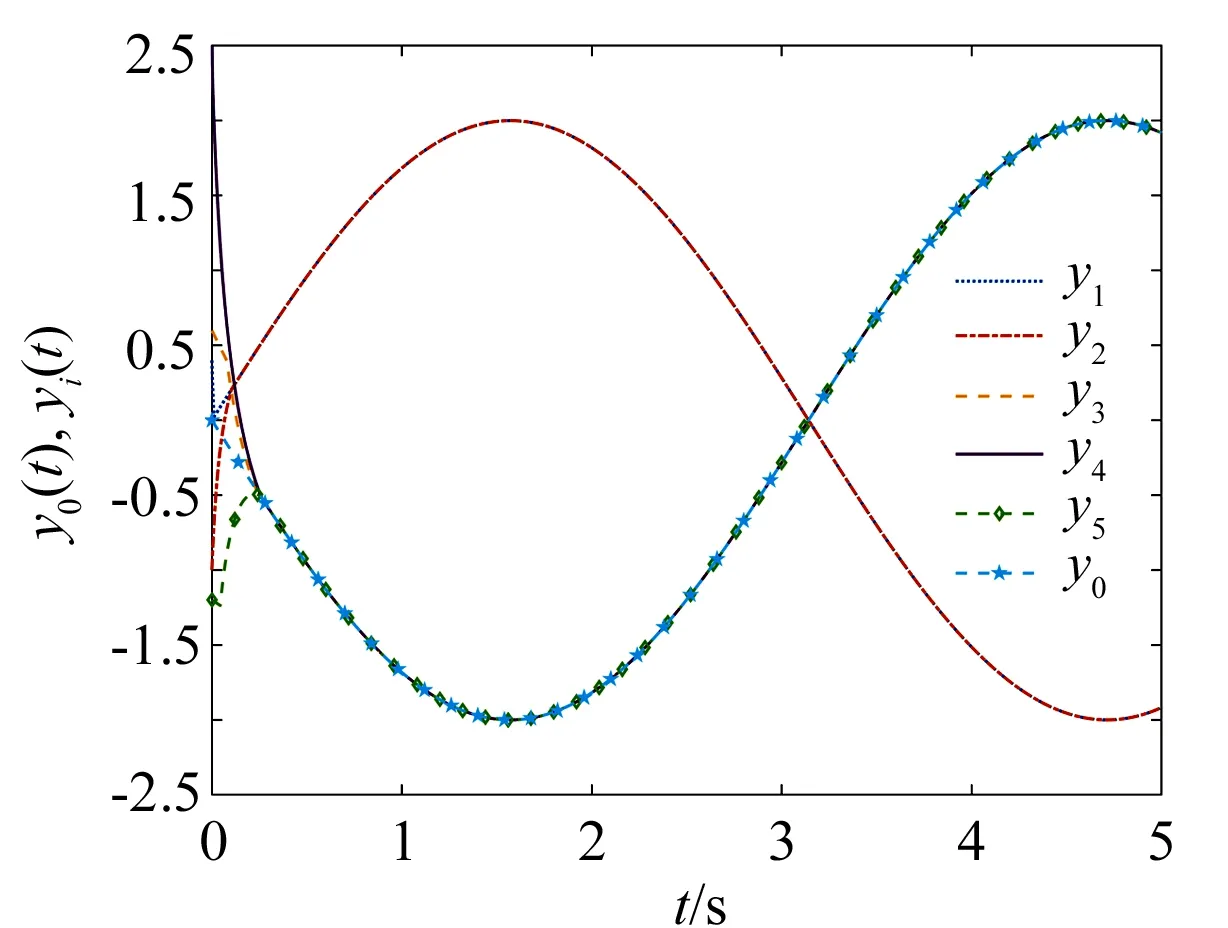
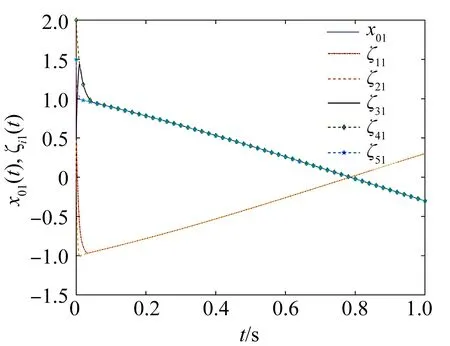
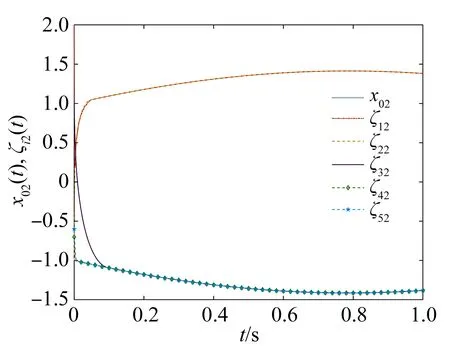
其中a>1,0 引理3[17]令x1,x2,…,xN≥0,m>1,0 引理4[18]考虑系统 (3) 其中x∈Rn,f(x):Rn→Rn连续,并且f(0)=0.如果存在一个连续的正定径向无界函数V:Rn→R,使得对任意解x(t,x0),满足 假设4无向图G是强连通图,并且是结构平衡图,且至少存在一个跟随者可获得领导者的信息. 设计预设时间观测器来观测领导者的状态,其形式为 (4) 定义误差ρi(t)=ξi(t)-dix0(t),则 (5) 定理1对于系统(1)及观测器(4),若假设1—4成立,且满足 证构造Lyapunov泛函V(t)=ρT(t)(M⊗K)ρ(t).对V(t)沿误差系统(5)求导,得 根据引理2,得 接下来,证明系统(1),(2)可以实现预设时间输出一致,设计控制器 (6) 令φi(t)=xi(t)-Φiξi(t),则 当t>T1时,zi(t)=0,则 从而 (7) 定理2对于异质多智能体系统(1),(2),假设1—4成立,如果控制器(6)中的参数S1i,S2i,S3i满足 S2i=Ui-S1iΦi, (8) BiS3i=I, (9) Ai+BiS1i<0, (10) 则(1),(2)将达到预设时间输出二分一致,且收敛时间上界为T1+T2. 证由条件(8),可得 Aixi(t)+BiS1ixi(t)+BiS2iξi(t)-ΦiA0ξi(t)=(Ai+BiS1i)φi(t), (11) 结合式(7)和(11),得 (12) (13) 由条件(10),可得φT(t)(A+BS1)φ(t)<0.进一步有 yi(t)-diy0(t)=CiΦiξi(t)-diC0x0(t)=diCiΦix0(t)-diC0x0(t). 基于假设2,得CiΦi=C0,则yi(t)-diy0(t)=0. 综上,异质多智能体系统(1),(2)实现预设时间输出二分一致,其收敛时间上界为T1+T2. 假设5有向图G是结构平衡图且包含一棵有向生成树,其领导者节点为根节点. 设计观测器 (14) 定义误差εi(t)=ζi(t)-dix0(t),则 (15) (16) 定理3对于异质多智能体系统(1)及观测器(14),若假设1—3,5成立,且 (17) 记sigη(ri(t))=(sigη(ri1(t)),sigη(ri2(t)),…,sigη(rin0(t)))T,sigθ(ri(t))=(sigθ(ri1(t)),sigθ(ri2(t)),…,sigθ(rin0(t)))T,可得 (18) 记p(t)=(sigη(r1(t))+sigθ(r1(t)),sigη(r2(t))+sigθ(r2(t)),…,sigη(rN(t))+sigθ(rN(t)))T,则 (19) 其中 (20) 由r(t)=(M⊗In0)ε(t),可得 (21) (22) (23) 结合式(22),(23)式,得 (24) (25) 结合式(24),(25),得 接下来,证明系统(1),(2)可以实现预设时间输出一致.为此,设计控制器 (26) 定理4对于异质多智能体系统(1),(2),若假设1—3,5成立,且控制器(26)中参数Q1i,Q2i,Q3i满足 Q2i=Ui-Q1iΦi,BiQ3i=I,Ai+BiQ1i<0, 则(1),(2)将达到预设时间输出二分一致,且收敛时间上界为T3+T4. 分别考虑无向图(图1)和有向图(图2)下的异质多智能体系统的预设时间输出二分一致.在仿真中,考虑异质多智能体系统包含一个领导者节点(标记为0)和5个跟随者节点(标记为1—5).将跟随者节点划分为2个子集V1={1,2},V2={3,4,5},相应地,D=diag(-1,-1,1,1,1).令xi(t)=(xi1(t),xi2(t))T,系统(1),(2)中的其余参数设计为 相应的矩阵参数设计为 图1 无向图Fig.1 Undirected graph 图2 有向图Fig.2 Directed graph 图3 观测器ξ(t)第1维分量的状态轨迹Fig.3 State trajectories of x01(t),ξi1(t) 图4 观测器ξ(t)第2维分量的状态轨迹Fig.4 State trajectories of x02(t),ξi2(t) 图5 定理2中y0(t),yi(t)的状态轨迹Fig.5 State trajectories of y0(t),yi(t) in Theorem 2 图6 观测器ζ(t)第1维分量的状态轨迹Fig.6 State trajectories of x01(t),ζi1(t) 图7 观测器ζ(t)第2维分量的状态轨迹Fig.7 State trajectories of x02(t),ζi2(t) 图8 定理4中y0(t),yi(t)的状态轨迹Fig.8 State trajectories of y0(t),yi(t) in Theorem 4 在无向图与有向图下研究异质多智能体系统的预设时间输出二分一致问题.设计了预设时间观测器来估计领导者的状态.通过设计预设时间控制器,提出相应的同步判别准则,保证了异质多智能体系统实现预设时间输出二分一致.最后通过数值仿真,验证了理论结果的有效性与可行性.
2 主要结果
2.1 无向图下异质多智能体的预设时间输出二分一致




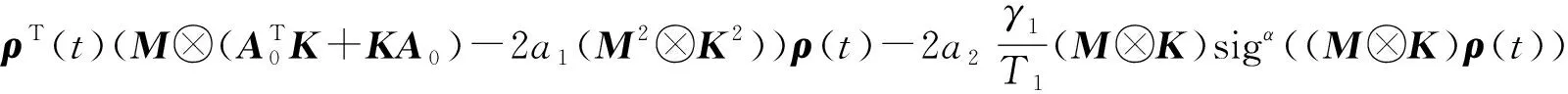
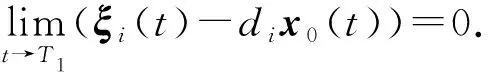
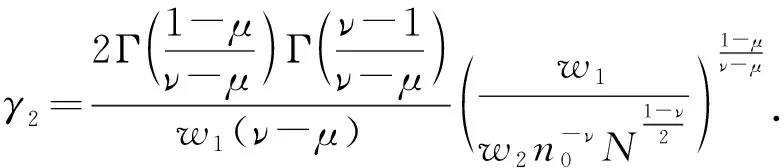

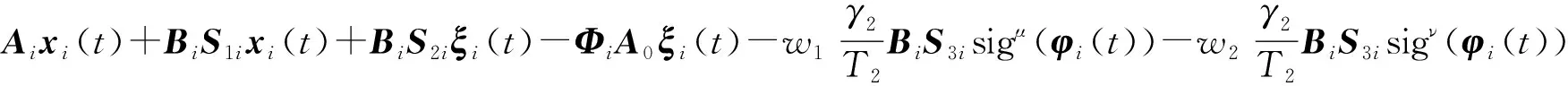

2.2 有向图下异质多智能体的预设时间输出二分一致
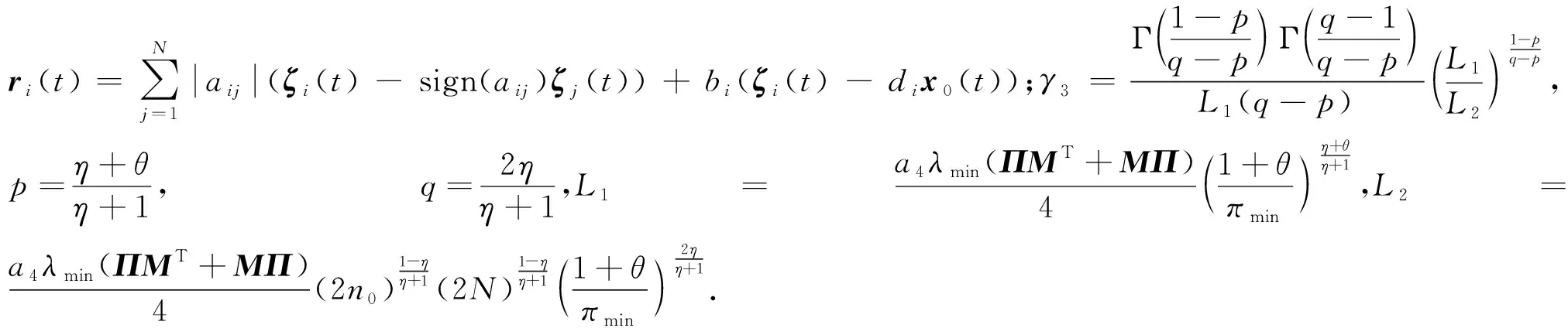
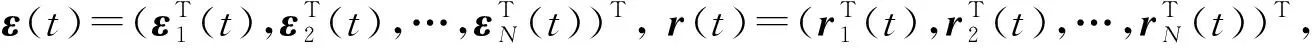

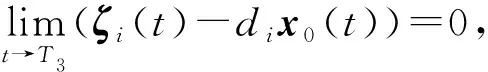



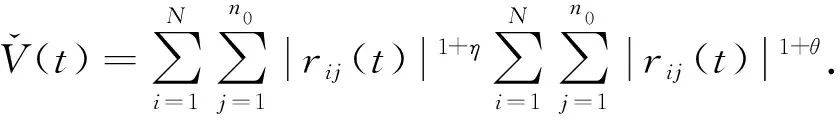
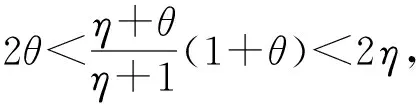
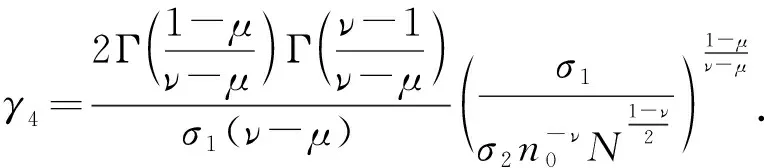
3 数值仿真

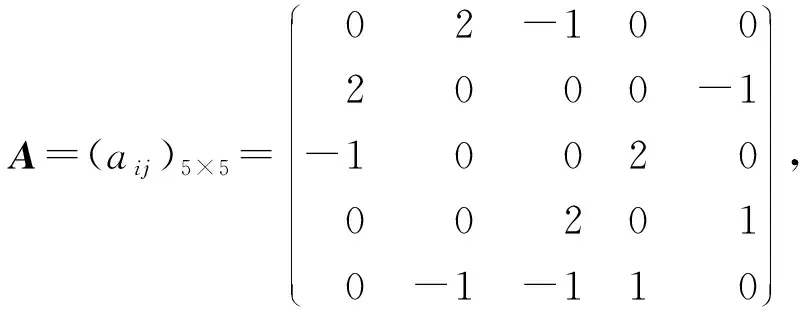
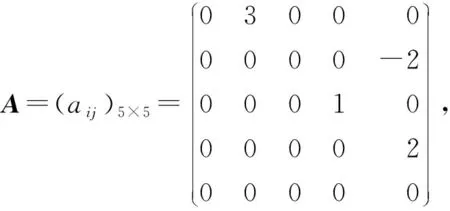

4 结语
