回归本质想方法,一题多解显思维——2021年广州市中考数学第25题评析与教学反思

中山大学附属中学(510275) 刘子奇

1 原题呈现

如图,在菱形ABCD中,∠DAB=60°,AB=2,点E为边AB上一个动点,延长BA到点F,使AF=AE,且CF、DE相交于点G.

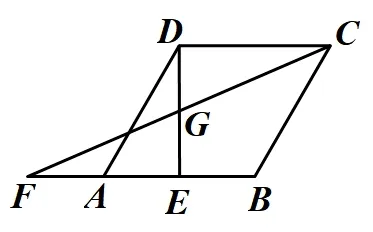
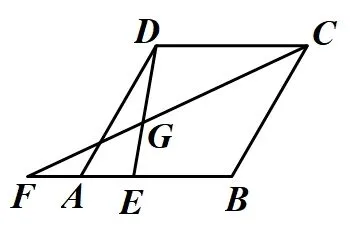
备用图

(1)当点E运动到AB中点时,证明:四边形DFEC是平行四边形;

(2)当CG=2 时,求AE的长;

(3)当点E从点A开始向右运动到点B时,求点G运动路径的长度.

2 试题特色

本题从基本图形菱形出发,综合考查多个知识点,包括菱形的性质,中点的定义,平行四边形的判定,含30°的直角三角形的性质,勾股定理,解一元二次方程,相似三角形的性质和判定,等腰(边)三角形的性质和判定,隐圆及圆的内接四边形性质,动点问题,轴对称变换,动点轨迹问题.本题的考查起点低,但是综合来看既有深度,又有广度,既考验高层次学生的思维,也考察到了低层次学生的简单理解和分析,所谓高低层次均有覆盖,中等层次都有设计,不同层次的学生都有机会着手解答问题,如第(1)问就只需学生明白平行四边形的简单判定,计算相应线段的长度即可快速解决问题.考查的知识点多样,考生需要在考场上快速联想相应的知识结构来构建解题框架和分析方法,有良好几何分析习惯的考生有机会展示自身的知识储备.问题的呈现,沿袭了几年来广州中考压轴题的风格,不拘于常规表达,既注重考查考生概念的本质的理解,又重视对考生数学思想方法运用的考查,最大限度的避免模型化的解题思路和解题方法,真正关注优等生的数学核心素养和综合能力,鼓励考生从不同角度思考和分析问题,考生可构思解决问题的途径及策略十分多样,在推理过程中综合体现不同的数学思想方法,此题更好的体现了当下对学生创造性思维的培养方向,更体现了广州中考数学压轴题的选拔功能.

3 解法溯源

本题是以四边形中的特殊图形——菱形为基础展开研究,第(1)问四边形DFEC是平行四边形,利用一组对边平行且相等即可证明;第(2)问是在限定条件下求静态线段的长度,在这个过程中证明ΔFGE为等腰三角形有两种不同的方式,体现出两种不同的思维方式,一是通过角来求证边之间的关系,一是通过线段比例来求证边之间的等量关系,在FG=FE的基础上求AE的长又有两种不同的思考方式,一是从勾股定理的角度出发求线段长度,二是通过利用菱形边的等量关系,联想圆的相关知识,构造辅助圆,进而利用基本的相似图形构建线段比例关系求解;第(3)问在前面两问的基础上进深度挖掘,以点的轨迹为考察方向,对动点轨迹问题进行全面考察,动态问题静态分析是主要的解题思路,具有良好解题习惯的考生,能够在解题过程注重解题的方向,大胆猜想,敢于动手,画出图形,临界分析,对于复杂图形的抽象分析要求考生有强大而稳定的心理素质,小心求证,寻求点E的运动轨迹与点G运动轨迹之间的相关性,在画出基本图形的基础上,灵活建构解题思路、选择最优方案解题.

4 问题解决

对于第(1)问,只需得到EF=CD即可求证,此问不作赘述,以下重点求解分析第(2)(3)问.

4.1 以形助数,构建一元二次方程求解线段长度

第(2)问求解分析:貌似与第(1)问之间不具有太大的相关性,实际上在(1)问平行四边形的证明基础上,通过回归联想平行四边形的本质属性即平行来思考线段之间的转化和图形之间的相关性.

根据题目所给的已知条件,我们需要从边平行以及线段相等两个角度相结合出发,去思考在求解AE之前需要与之相关的什么条件,毫无疑问,AE与AF相关,即需求解与EF相关的线段或者几何图形,因此需要先解决ΔFEG与所要求解的线段之间的关系在哪,方可继续思考线段AE的长度,以下给出两种思考方式.

方法一设AE=AF=m,∵CD=CG=2,则ΔCDG为等腰三角形,∴∠CDG=∠CGD,则在菱形ABCD中,AB//CD,∴∠CDG=∠FEG,又∵∠EGF=∠CGD,∴∠EGF=∠FEG,∴FG=FE=2m.

方法二∵四边形ABCD是菱形,∴CD//EF,∴ΔCDG∽ΔFEG,∴∴EF=FG,即FG=2AE=2m.

在以上的两种解法中,都涉及到一个核心本质问题,即所给图形与所求问题之间的核心联系,回归本质看核心,是解决问题的关键,而此处的关键即为证明为等腰三角形,在证明ΔFEG与所求线段ΔFEG的长度的关系之后,又有以下两种方式来求解线段长度.

一为勾股法,即通过构造直角三角形建立一元二次方程直接求解线段长度.

如图(1)所示,作CP⊥BP,在RtΔCBP中,∠CBP=60°,BC=2,CH=BP=1,在RtΔCFP中,CF=2+2m,CP=FP=3+m,CF2=CP2+FP2,即(2+2m)2=+(3+m)2,整理得:3m2+2m−8=0,解得:m1=m2=−2(不合题意,舍去),∴AE=

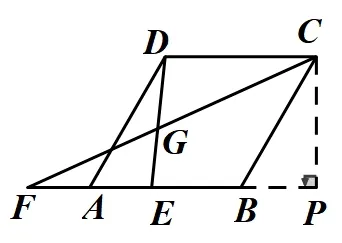
图1

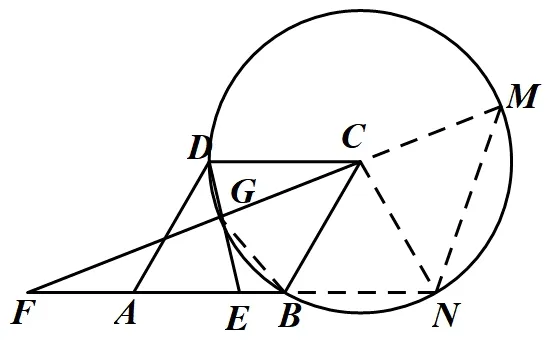
图2

二为构造法,通过题目所给线段相等的条件,回归线段相等的基本构造方法,利用等线段构造出一个隐藏在菱形上的半径为2 的圆,此种方法问题在于将基本图形复杂化,虽说有点过于牵强,但是却能实实在在反应出考生对于几何知识的综合应用能力,也能体现出考生在一题多解时的各种角度思考,能够从复杂图形中抽象出简单基本图形以达到简化问题分析是学生在面对几何难题时所需要掌握的基本技能,但是若能在简单图形中构造能够帮助解决问题的复杂图形也不失为一种综合能力的体现.

如图(2)所示,以点C为圆心,2 为半径画圆,则点D、B、G都在圆C上,延长FC交圆C于点M,延长FB交圆C于点N,连接BG,CN,∵四边形BNMG为圆C的内接四边形,∴∠GBN+∠M=180°,又∵∠GBN+∠GBF=180°,∴∠M=∠GBF,又∵∠F=∠F,∴ΔFBG∽ΔFMN,即FG·FM=FB·FN,∵∠CBN=∠DAB=60°,CB=CN=2,∴ΔBCN为等边三角形,∴BN=2,∴2m(2m+4)=(m+2)(m+4),解得m1=m2=−2(不合题意,舍去),∴AE=

在以上的问题分析过程中,从题目本身的问题结构出发,求解线段长度在初中数学体系中即是通过勾股定理构建一元二次方程,以及通过相似建立线段比例关系进而转化为方程求解,两种方式殊途同归,各有其优势所在,勾股法属于常见的解题方法,构造隐圆虽说有把问题复杂化的嫌疑,但是对于优等生的解题思维的体现是显而易见的,在图形复杂化的过程中,优化解题思路,找寻自己的最有解题方案是考场上必备的解题技巧.

4.2 以形解形,构建相似图形分析运动轨迹

第(3)问求解分析:此问以线上动点问题为背景,探讨主动点与从动点的轨迹相关性问题,由点E沿着线段AB运动,即可猜想点G的运动轨迹是否也是沿着某条直线进行运动,由此大胆猜想,再以临界法的方式分析起始点和终点位置情况,因此大致知晓点的运动轨迹情况,再在此基础上进行小心求证,从而得出点G的运动路径即是一条线段.

以下通过证明在运动过程中,线段AG所在的三角形中保持三角函数值不发生改变,从而得出点的运动轨迹为一条线段.

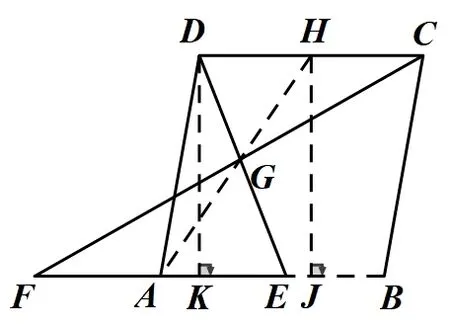
图3

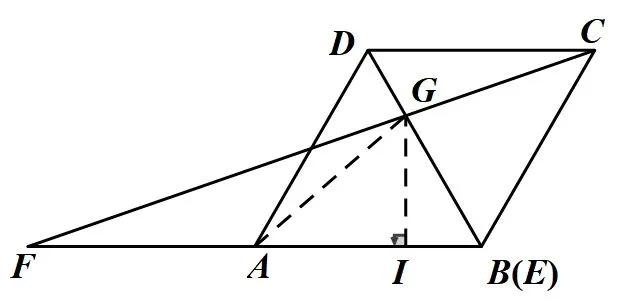
图4

如图(3),(注: 此图仅作为证明AG轨迹用),延长线段AG交CD于H,作HJ⊥AB于J,作DK⊥AB于K,∵四边形ABCD是菱形,∴BF//CD,∴ΔDHG∽ΔEGA,ΔHGC∽ΔAGF,∴∵AE=AF,则点H为CD的中点,∴DH=CH=

在RtΔADK中,AD=2,∠DAB=60°.∴DK=AK=1,在RtΔAHJ中,HJ=DK=AJ=AK+JK=AK+DH=2,此时点J与点B重合,∴tan ∠HAJ=则G点轨迹为线段AG.∴G点轨迹是线段AG.∴当点E与点B重合时,如图(4)所示,过点G作GI⊥AB于点I,∵四边形ABCD为菱形,∠DAB=60°,AB=2,∴CD//BF,BD=2,∴ΔCDG∽ΔFBG,即BG=2DG,∵BG+DG=BD=2,∴BG=在RtΔGIB中,BG=∠DBA=60°,在RtΔAIG中,∴G点路径长度为

此外在求证点G的轨迹为一条线段之后还可通过以下方式来求解轨迹长度.

如图(5) 所示,过点H作HQ⊥AD交延长线于点Q,∵四边形ABCD为菱形,∠DAB=60°,AB=2,∴CD//BF,DH=1,∴ΔDGH∽ΔBGA,∴即AG=2GH,∴DQ=1,HQ=则在RtΔAPQ中,点运动的路径长度为

当明确点的轨迹为线段时,第(3)问本质问题即可归结为求线段的长处,其解题思路与方法基本与第(2)问如出一辙,通过构造直角三角形利用勾股定理求解,抑或通过构造相似三角形利用对应边成比例进行求解,此两种方法均为初中平面结合求解线段的常用方法以及需要考生熟练掌握的解题方式,在固有思维的基础上进行拓展延伸,就是最好的思维训练方式.此外鉴于是平面几何问题求解线段长度,那代几综合自然也是一种解题方式,因此第(2),(3)问均可通过建立平面直角坐标系来解决问题.

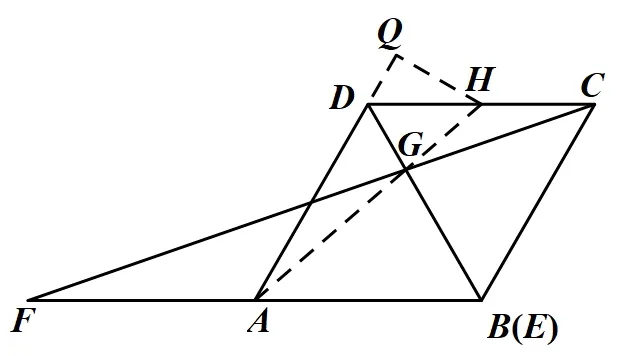
图5

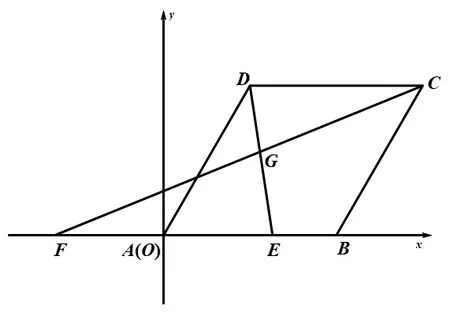
图6

4.3 数形结合,建立坐标系求解线段长度

因菱形所具有的特殊性,在初中阶段考察得特别常见,作为学习矩形和正方形的基本图形,自然可以与矩形及正方形的特殊性联系在一起,且在菱形中存在两种特殊的三角形——直角三角形和等腰三角形,两种三角形都可与直角相联系,因此在求解线段长度,尤其是动点轨迹问题时可以通过建立平面直角坐标系来解决问题.

第(2)问解析: 如图(6) 所示,以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,则由题可知设E(a,0)(0≤a≤2),则F(−a,0),∴直线CF的解析式为:y=直线DE的解析式为:y=解得则直线CF与直线DE的交点G的坐标为当CG=2 时,化简得3a2+2a−8=0,解得a2=−2(不合题意,舍去),∴

第(3)问解析: 设G(x,y),由(2)可知x=则有y=∵0≤a≤2,则0≤x≤∴点G的运动轨迹为y=当点E在点A处,即a=0 时,此时x=0,则点G与点A(0,0)重合,当点E在点A处,即a=2 时,此时x=则点G的坐标为点运动的路径长度为

几何问题通过代数方法解决,是学生在思考几何图形难于推导其逻辑关系时最常用的一种方法,再者代几综合是中考中的常考方向,考生通过数形结合的方式来解决压轴题,是考生所必须要掌握的一个基本技能.此外几何问题通过代数分析建立平面直角坐标系解决问题,有时候能够起到事半功倍的效果,能够大大节省思考时间,简化解题思路,此题即是一个很好的例子.

5 解题反思

广州市中考力求在微观变化中谋求创新和突破.2021年的这一题在菱形的基础上展开,考察基本的平行四边形的判定、固定线段的长度以及动点轨迹长度.在本着既考察学生的综合能力也考察学生的数学核心素养问题的出发点,此题巧妙地避开了所有套路化的解题方式和模型化的解题思维,在解决问题时学生需要感知图形的特征,要通过形来思考数的作用,通过数来想图形的变化,在数形结合的过程中去联想与题干条件相关的知识要点以及解题方向,学生需要从“数形互换”中体会不同角度思考问题的有效性,能够创造性的去解决问题.通过一题多解的方式体现,实际上,这道题用代数法(建立平面直角坐标系)解决最佳,既能避免学生过渡思考以致浪费时间,达到简化解题思路,也能让学生更直观的理解图形的特征,达到正确求解.全国各地的中考压轴题都既可以从几何角度思考,又可以从代数角度思考,通过解法的多样性拓展解题思路,优化解题方法.

6 教学启示

6.1 重基础夯实,构建知识框架

对基础知识的掌握,基本解题方法的灵活运用是展现正确解题的前提条件.在教学过程中教师应力戒各种知识点的灌输和堆砌,在恰当的情境引入下让学生着重理解基本概念、定义、定理以及基本原理的发现和理解,如菱形的定义和判定,不应一味的告知,而是在平行四边形的基础上类比学习,在平行四边形的前提上去理解,这样才能够在之后的学习过慢慢构建起整个四边形知识的框架,由浅入深,由表及里,这样的一种教学方式才符合人们对事物的认知和理解的事实规律,从而构建起整个知识体系的内在逻辑框架,学生才能有一个底层基础知识水平.

逻辑推理是几何分析的必要条件,逻辑推理是指从一些事实和命题出发,对事物进行观察、比较、分析、综合、抽象、概括、判断、推理的能力,采用科学的逻辑方法,准确而有条理地表达自己思维过程的能力.因此在逻辑推理过程中并不是完整并规范的的表述解题过程,而是在这一过程中,因为有严谨的逻辑推理才能有规范的表述,而这些的前提条件是在基础知识的结构下具有完备的逻辑框架.

6.2 重理解分析,形成经验积累

如果学生缺乏对题目的理解,自然不知如何分析,在课堂上教师应教会学生理解题的语言描述,在这一过程中,选题是重要的一环,学生的自我语言陈述同样如此,在审题过程中,教会学生分析题干中的主要部分,即未知量,已知数据以及条件,并能够从各个方面来考虑题干中的主要部分,通过这一方式的训练和思考,充分分析并理解题意,形成经验并积累成自身的解题方法.

在学生充分理解分析的基础上,在完成解题之后,教师因适时引导学生对所解问题进行及时的总结、分析和复盘,其中所涉及到的解题方法,所包含的数学思想,所突出的知识结构,所涉及到的基本概念和定义都是值得复盘的要点,借此学生能够及时的构建相关的知识结构与知识系统,能够在解类似问题时快速地联想相关知识.

初中平面几何基本上都是以基本图形构建起的复杂图形展开研究和探讨的,在这些图形中包含这我们平常在新课讲授过程中所遇到的基本简单图形,其中自然就有与之相关的基本知识要点,如与等腰三角形相关的基本图形在四边形的各个章节里都有出现,在圆中更是如此,教师在教学中引导学生自我归纳和总结与等腰三角形相关的基本图形,让学生在遇到等腰三角形时需要注意些什么,可以联想到什么,可以构建出什么有助于解决问题的图形……,学生在归纳和总结中发现知识内部之间的联系,有助于提高学生在改变问题情境下准确并快速把握核心知识、找到最有解题策略的能力,能够意识到万变不离其宗,从而做到举一反三,准确并有效地运用已有知识经验解决新问题的能力.

6.3 重深度思考,回归问题本质

深度思考是当下学科教学的重要共性认知,在初中数学的教学中显得尤其重要,教师在平常的教学中要为学生做深度思考的指导和训练,在日常的思维训练和解题训练中持续给学生展开深入学习和思考提供一定的启迪和帮助,巩固学科教学成果,全面培养学生核心素养.

在深度思考训练的过程中问题的设计和提出在课堂上是一项十分有效的措施,在分析问题时题干的连接性,教师需要深度解析,在讲授新课时,教学内容需要教师进行深度解析,找到学生与知识或问题本身之间的思维切入点,这样才能给出更为准确的激发和调动.如在人教版八年级数学上册“全等三角形”的教学时,教师对教材内容做深度研究,从情境导入展开问题渗透,问题设计体现梯度性,从平移、翻折、旋转等角度展开思考,考查两个三角形全等的操作方法.如:如何准确对全等三角形的对应元素做对接思考? 针对特定三角形,能够找到对应的元素吗? 如何利用全等三角形解决一些实际问题? ……通过这一系列问题的深度思考让学生体会到三角形全等的本质属性.

教师在课堂上或者在习题讲解过程中,通过启发式的方式给学生提供更多思考的机会,在一系列问题展现的过程中进行深度思考.经常长期的训练,学生慢慢对问题形成系统性考虑,思考角度选择、思考体验总结、思考方向调整等等.让问题与深度思考展开全面对接可以给学生带来丰富学习启迪.深度思考对学生提出更高要求,能拓宽学生数学思维视野,学生也能在深度思考的过程中培养发散思维、逆向思维、探索思维、归化思维,在运行过程中建立学科核心素养,进行深度思考,实现深度学习目标.