考虑非平稳过程的劣化钢筋混凝土梁桥时变可靠度分析
2022-06-16金聪鹤钱永久徐望喜
金聪鹤,钱永久,张 方,徐望喜
西南交通大学土木工程学院,成都 610031
我国为数众多的公路桥梁受到强度和频率均随时间增大的车辆荷载作用,长期处于“带病工作”状态,承载能力衰减速度远超预期,安全问题日益严峻[1−2].由于资金和人力所限,不可能总是对所有在役桥梁进行及时检测和彻底维修加固.为了保证桥梁结构的正常运营,需要在可靠度框架下对其进行安全性能评估,以作为后续管理、养护、加固与维修的依据[3].
依据现行《工程结构可靠性设计统一标准》[4],不考虑桥梁承载力随时间的衰减,基于极限状态设计原则计算结构当前时刻的可靠度指标β,可能会高估结构的可靠性,不利于对其进行安全性能评估.为了考虑桥梁抗力的时变效应,Mori和Ellingwood[5]于1993年提出了“时变可靠度”理论:采用平稳Poisson过程描述考察时段(0,T)作用于结构、服从同一分布的离散化荷载随机变量,其中泊松分布的参数λ表示荷载出现的频率;将时变抗力表示为初始抗力R0和抗力衰减函数g(t)的乘积[6],提出了时变可靠度计算公式.该理论能够考虑桥梁抗力随时间衰减的效应,成为了当前工程结构可靠度领域研究的热点[7−9].
叶新一等[3]基于Mori-Ellingwood公式的Taylor级数展开将积分运算转化为代数运算;Li等[7]提出了考虑结构劣化和荷载增长非线性的时变可靠度模型;李全旺和王草[10]采用迭代算法生成服从同一正态分布的关联荷载样本,金聪鹤等[9]基于n元Copula函数生成关联随机数的方法,讨论了荷载相关性强弱对桥梁时变可靠度的影响;袁阳光和许昕[11]基于Gamma随机过程提出了时变抗力非平稳劣化模型; Zhang等[12]基于自适应采样法提出了近似最可能点轨迹(AMPTT)分析法,将系统时变响应转化为高斯过程进行可靠度计算.近年来,计算机性能的提升使得许多近似算法被用来处理系统可靠性问题,例如等效随机过程转换法[8],或采用Kriging自适应模型来进行多变量系统时变可靠度的计算[13−14];Dai等[15]和谭晓慧等[16]采用多项式混沌展开(PCE)和Karhunen−Loeve展开对非平稳非高斯过程进行有效模拟;张永峰和陆志强[17]提出了基于卷积神经网络的构件剩余寿命预估模型.上述方法对建立抗力、荷载分布类型和参数都不同的非平稳时变可靠度模型提供了思路.
另一方面,桥梁服役期间可能经受了高强度历史荷载的验证,即使不存在显著外观损伤,其后继服役期的安全性能未必乐观.因此对在役桥梁进行安全性能评价,需要考虑历史荷载信息对桥梁时变抗力的验证作用[18−20].既有研究[3,9,10,20−22]中,荷载随机变量在等时间间隔的重现频率是一定的,即λ为常数.然而,车流量和车辆荷重均会随着桥梁服役而增大[22−23].若不考虑车载强度或频率随时间增大的效应,均会低估桥梁失效的风险.为解决这些问题,王草[22]将 Mori−Ellingwood公式中车载强度均值表示为u0+ut的线性形式,其中u0和u分别为初始均值和年均增量.Li等[7]提出了荷载频率函数λ(t)的概念,不论在平稳或非平稳随机过程中均适用.
然而,对基于历史荷载验证的在役桥梁进行安全性能评价,首先需要对当前时刻抗力分布进行重新评估[9,20],这往往需要超过10万次蒙特卡洛模拟(MCS)过程,若考虑荷载为非平稳过程且具备相关性,则需要花费大量时间.为了提升桥梁安全性能评估的效率,本文基于MCS实验剔除失效抗力样本的原理,将服从对数正态分布抗力的变异系数假设为时间变量,兼顾荷载频率随时间增大的效应,提出了基于非平稳随机过程的在役桥梁时变可靠度计算方法.
1 基于验证荷载实验的时变可靠度分析方法
如图1所示,横轴表示桥梁服役时间t,纵轴表示作用力F,包括抗力及荷载强度.在评估期(0,T)内任意时刻t的桥梁承载力记为R(t),作用于结构的荷载效应表示为随机过程S(t).设Prel(T)表示结构在评估期内的时变可靠度,则:

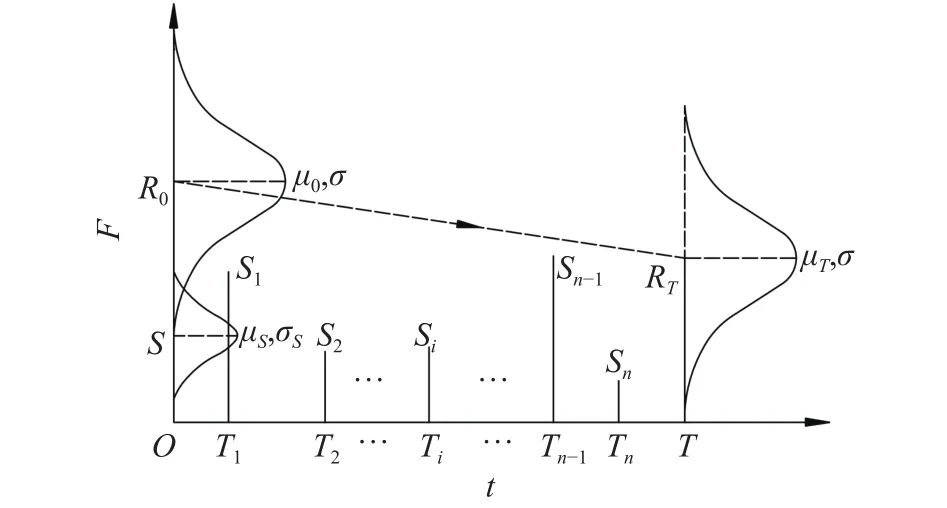
图1 Poisson 随机过程示意图Fig.1 Sketch of Poisson stochastic process
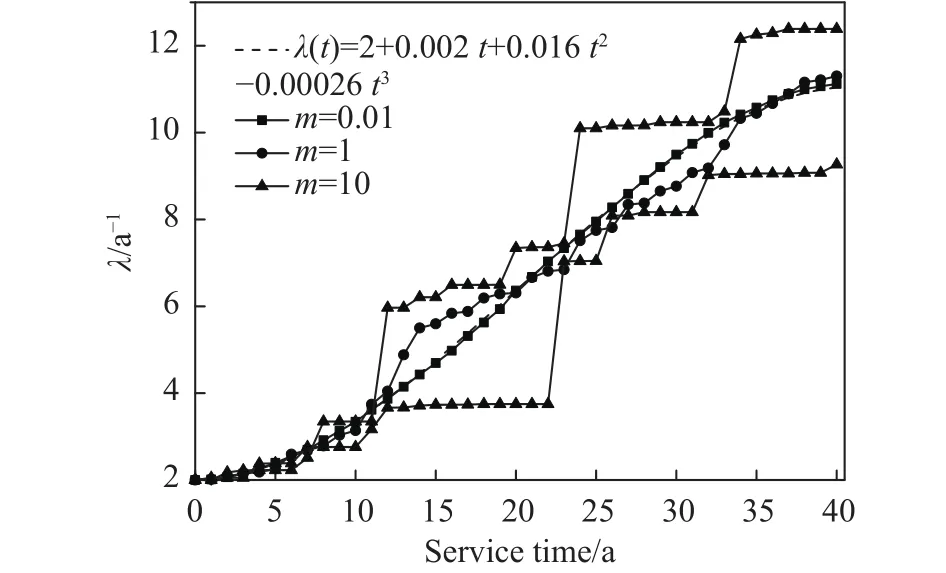
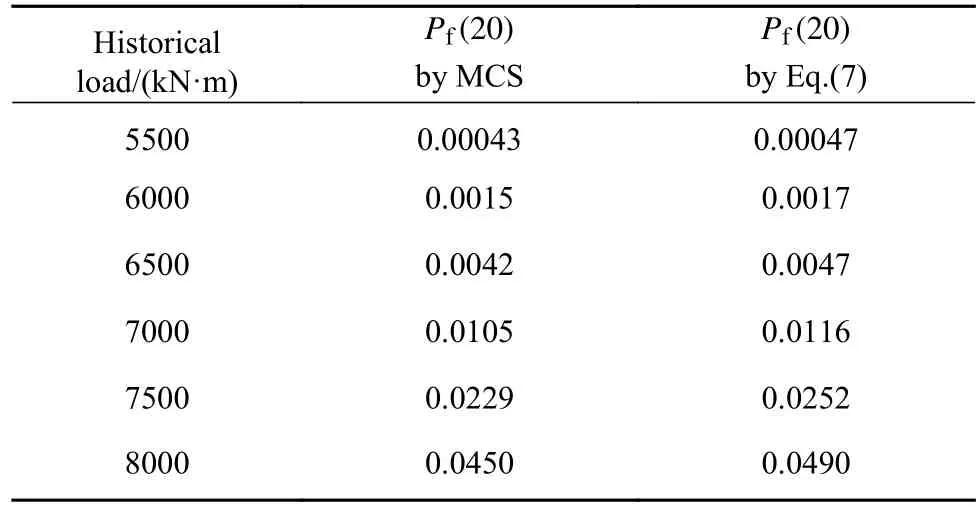
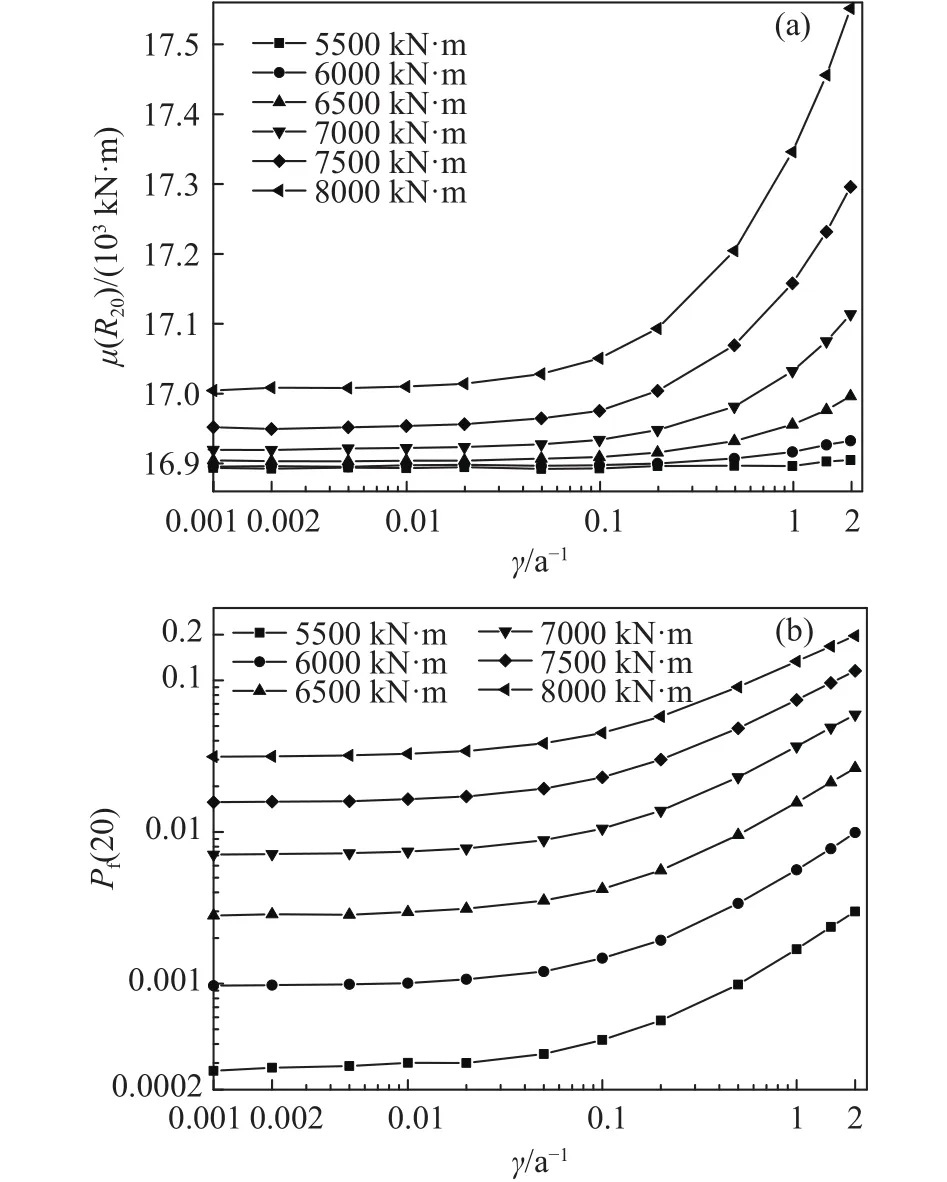
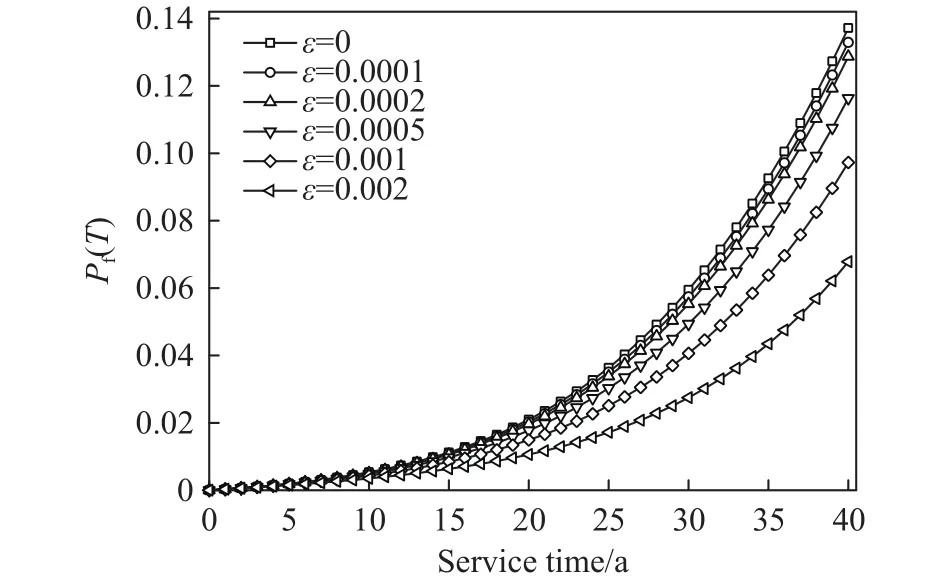
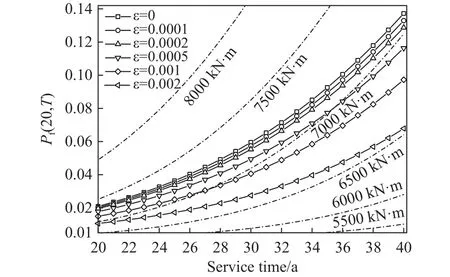
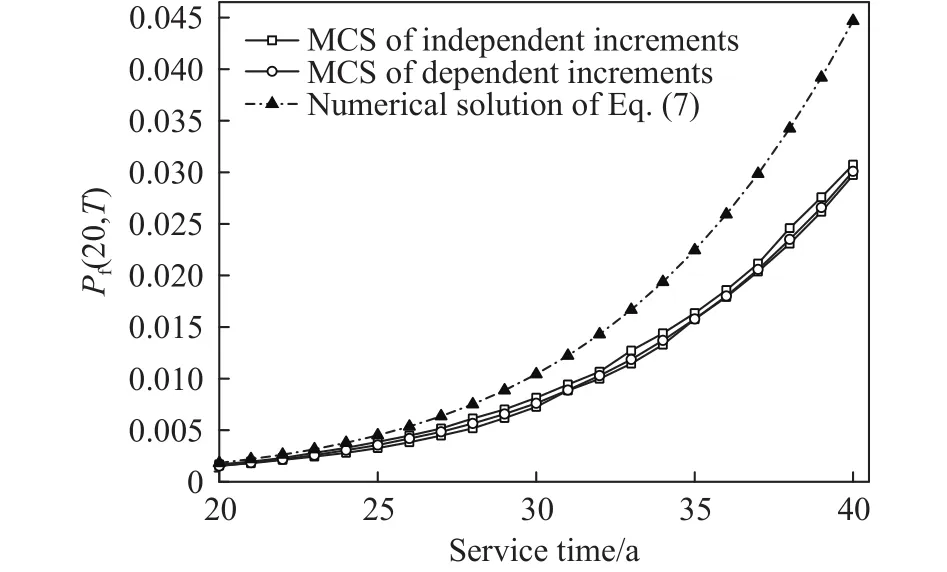
这段时间内发生的荷载效应次数n服从参数为λ的Poisson分布,记为S1,S2,...,Sn,如图1所示,对应的发生时刻为0 上式即Mori−Ellingwood时变可靠度公式,被国际ISO《在役结构评估规范》所推荐[3],是时变可靠度研究中最重要的公式之一.假设某桥梁已服役T1时长(0 然而,通过验证荷载实验仅意味着桥梁在T1时刻承载力的下限[18],也表明结构在考察时段内只进行了一次验证荷载试验,会导致评估结果并不准确.李全旺等[20]基于抗力劣化与衰减函数完全线性相关的假设,将服役时长划分为n个区间,其中第i个区间(i=1,2,...,n)(ti−1,ti]的最大荷载效应Si的CDF为FS,i(s),提出了劣化抗力R1的PDFfR1(r)的计算公式: 其中,Si的均值和方差可以依据实测荷载谱采用非参数外推法等统计方法获得[25].通常当MCS实验次数超过10万时,式(5)和MCS得出的fR1(r)分布结果几乎相同.上述情况基于非平稳荷载效应彼此完全独立.金聪鹤等[9]通过大量MCS实验表明:荷载相关性越强,对T1时刻抗力的验证作用越不显著.因此,为了增强历史荷载的验证效果,本文不考虑车辆荷载之间的相关性. 设h(t)表示结构的灾害函数,定义为结构成功服役 (0,t)时段后,在t+Δt时刻发生破坏[6−7].表示为:采用频率函数λ(t)代替常数λ,将式(6)代入式(3),整理得: 若不考虑疲劳效应,钢筋锈蚀是钢筋混凝土构件抗力退化的主要原因;衰减函数g(t)可采用下式计算[26]: 其中,t0是结构服役到开始发生锈蚀所经历的时间;k1和k2是参数.依据此式计算T1时刻劣化抗力的理论均值. 桥梁服役以来,每日车辆的通勤次数并非单调递增,但以一个时期的总体数量或平均值计,则表现出非平稳增长的特性[23].因此,可以采用袁阳光和许昕[11]提出的Gamma随机过程方法说明频率函数进行可靠度计算的合理性. 据统计,新建桥梁在服役第10年的日均车流量约为第1年的3至4倍,且在随后的服役期呈现更快的增长趋势[23].按照不同荷重的车辆等概率出现的原则,设T=0时刻某强度的最大车辆荷载频率为一年两次,即λ(t=0)=2 a−1,在第 40 年的荷载频率约为第1年的5.5至6倍,可以采用一次、二次和三次函数来描述频率函数λ(t)如下: 对应的λ(40)依次为 11.2,12和11.04 a−1.频率函数如图2所示. 图2 荷载频率函数图Fig.2 Diagram of load frequency function 现考虑λ(t)对应的等效Gamma非平稳过程.将考察期(0,T)分为n个等区间的时间间隔(0,T1),(T1,T2),···,(Tn−1,T),每一个时间间隔(Ti−1,Ti)(i=1,2,…,n)的Gamma增量Δλ(Ti)表示为该间隔的平均增量i和一个服从相同Gamma分布的独立随机变量序列χ={χ1,χ2,···χn}中第i个元素χi的乘积:Δλ(Ti)=i·χi,其中T0=0,λ(T0)=2a−1.其中i依据相邻时段荷载频率增量是否相关,可分为独立增量i,I和关联增量i,D,分别表示为i,I=λ(Ti)−λ(T0)和i,D=λ(Ti)−λ(Ti−1),则λ(t)对应的等效Gamma随机过程(t)的表达式分别为[11]: 式 中,Γ(z)表示Gamma函 数, 设时间间隔为1 a,Δλ(Ti)分别考虑独立增量和关联增量的情形,调整尺度参数m进行模拟.三次函数的(t)模拟结果分别如图3和图4所示. 图3 不同尺度参数的(t)IFig.3 ( t)I with different scale parameters 图4 不同尺度参数的(t)DFig.4 ( t)D with different scale parameters 由图3和图4可知,尺度参数m越小,(t)越接近于λ(t),当m→0时,(t)与 λ(t)重合,表明了本文所提出方法的正确性. 根据时变可靠度的定义,在验证期(0,T1)内时变抗力低于任意历史荷载的桥梁结构是失效的,MCS将这种情况得到的R1值剔除[9,22].随着验证荷载强度增大,R1的均值增大,呈现正态分布—对数正态分布—广义极值分布的特性. 如图5所示,某桥梁结构已服役T1时长;(0,T1)时段内发生了j次荷载作用S1,i,S2,i,···,Sj,i,对应的发生时刻为T1,i,T2,i,···,Tj,i(0<T1<T,0 图5 抗力衰减与倒推初始抗力过程示意图Fig.5 Resistance degradation and process of initial resistance retrospection 若考虑历史荷载信息对T1时刻抗力的验证作用,可以将抗力变异系数ζ写为关于t的函数ζ(t): 其中,ζ=σ/μ0为初始抗力的变异系数,ε为参数.设fR0(r,ε,t)表示变异系数降低的初始抗力PDF,式(3)可写作: 通过修改参数ε,可以调整时变抗力R1的剔除程度,相当于结构在任意t∈(0,T1)都受到不同强度和频率的历史荷载的验证,因此是一个基于非平稳过程的时变可靠度计算公式.本文采用式(13)和基于频率函数的MCS结果作比较,以某在役桥梁为例,说明该公式的正确性,并对该桥后继服役期的安全性能进行评估. 四川省某预应力钢筋混凝土梁桥,依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》[27]和《公路桥涵设计通用规范》[28]分别对主梁进行正截面承载能力复核,可以得到除去恒载和行人荷载的跨中正截面承载力R0=20600 kN·m;依据《城市桥梁设计规范》[29]布置车道荷载计算跨中截面弯矩(不计剪应力影响),并进行验证荷载实验(图6),得到最大车辆荷载S和R0的比值为0.267(均以跨中弯矩计).依据当地经验,假设该荷载的初始频率为一年两遇,即λ=2 a−1.该桥梁为旧桥改造工程,设锈蚀发生的起始时间t0=0.现基于本文提出的时变可靠性分析方法,评估该桥在0~40 a的安全性. 图6 验证荷载实验现场Fig.6 Proof load test site 通过调整变异系数降低的参数ε,可依据式(13)直接进行时变可靠度计算.注意到该荷载强度相较于结构的极限承载力偏保守,故本文采用该比值以上的荷载作为最大车辆荷载效应的均值,选定0~40 a中的某时刻T1进行基于MCS的验后抗力参数统计,并将结果与本文公式进行比较. 若不考虑车辆荷载的高尾敏感性,通常建议采用极值I型分布进行描述[30],变异系数设为0.2.国内外关于钢筋混凝土梁的承载力统计表明:桥梁结构的初始承载力服从对数正态分布,ζ≈0.15[3,21].该地区属于亚热带湿润气候区,分别取k1=0.01、k2=0.00005[26]作为g(t)的参数. 为了充分评估结构的安全性能,不妨取T1=20 a,考虑 (t0,T1) 的“历史荷载信息”对结构在T1时刻抗力R1的验证效应,其中“历史荷载”强度均值为 5500、5750、···、8000 kN·m,固定频率λ=2 a−1,获得R1的统计参数,以讨论参数ε的取值范围.本实验中MCS次数均为1000万次. 其次,为了验证式(13)的准确性,分别采用强度均值为 5500、6000、···、8000 kN·m、频率函数为λ(t)=2+γt的“历史车载信息”进行验证荷载实验,其中γ为年均频率增量,t取整数;用式(7)求得结构在(T1,T)时段基于fR1(r)的时变可靠度,并与式(13)计算结果相比较.本实验中 5500~7500 kN·m 的所有MCS次数均为1000万次,8000 kN·m的模拟次数为500万. 最后,为验证Gamma过程中增量独立与否对计算结果的影响,采用均值为6000 kN·m,频率函数为式(9)的“历史荷载信息”进行R1的分布参数统计,将得到的fR1(r)进行时变可靠度模拟,并与式(7)的计算结果进行比较.本实验中所有MCS次数L=500万.当采用荷载频率可变的可靠度分析模型时,MCS步骤如下: (1)按照初始频率λ0,生成一个参数为λ0T1的Poisson随机数k. (2)在(0,T1]生成k个服从均匀分布的时间点T1 (4)由初始抗力的分布生成样本值r0,对i=1,2,···,n,生成对应时刻的抗力值ri=r0×g(ti). (5)根据“历史荷载”的分布,生成对应时刻的同分荷载样本值{s1,s2,···,sn}. (6)若对任意i=1,2,···,n都有ri>si成立,这表明结构在(0,T1]是可靠的,记录此时的r20=r0×g(20);否则表示结构没有通过服役荷载的验证,舍去此r20.统计结构可靠的模拟次数,以nl表示. (7)重复步骤 1至 6L次,根据记录的 nl次r20求得其均值和方差,当L足够大时,得出的均值和方差即为经过历史荷载验证的R1的分布参数,同时可以得出(0,T1]结构基于fR0(r)的时变可靠度=nl/L. 由于过大的历史荷载往往会对桥梁后继服役期安全性能带来隐患,因此不论是对在役桥梁,或本文中假设到T1时刻仍可靠的桥梁,期望的ε取值应当不大,否则变异系数减小过快,验后结果将失去参考意义. 通过计算得出T1时刻抗力理论均值和标准差分别为 16892 kN·m和2533.8 kN·m.表1 给出了经过验证荷载实验后,抗力R20的均值μ(R20)、标准差σ(R20)、变异系数CoV.和Pf(20)的变化情况,其中Pf(T)表示结构在考察期(0,T)内的时变失效概率,Pf(T)=1−Prel(T).由表1可知,当荷载频率相等时,μ(R20)随历史荷载强度增大而增大,σ(R20)则反之(σ> σ′);变异系数随着历史荷载均值增大而降低,证明了第三章分析的正确性;结构在8000 kN·m验证荷载强度(初始抗力均值的38.8%)作用下的Pf(20)=0.031;变异系数由0.15下降至0.1448,降低约3.5%,可以作为变异系数降低的参考标准:即当ζ=0.15且 ζ(t)为一次函数时,ε≤0.002. 表1 多强度历史荷载对R20的验证结果及时变失效概率Table 1 Verification of R20 by multi-intensity historical loads and timedependent failure probability 表2给出了频率增量γ=0.1 a−1时 MCS和式(7)计算结果的比较.为了直观起见,结果统一采用时变失效概率Pf(T)进行表示.两种方法得出的结果非常接近,其中荷载均值为8000 kN·m时二者的失效概率分别为0.045和0.049,相差近千分之四,说明当 λ ≤0.01 a−1、考察时段小于 20 a 时,公式(7)具有很高的精度. 表2 MCS 和式 (7)的 Pf(20)结果比较Table 2 Comparison of Pf(20) between MCS and Eq.(7) 图7分别给出了采用式(7)计算该桥梁基于fR0(r)的0~40 a时变可靠度Prel(T),及式(3)基于fR1(r)的20~40 a可靠度,以β值表示,即返回Prel(T)服从标准正态分布的反函数值.图例中,符号分别代表6个不同的历史荷载强度S的均值;虚线和实线分别代表式(7)和式(3)的计算结果.本文规定,若考察时段的起始时刻Ti>0,则采用Prel(Ti,T)的记法表示考察时段 (Ti,T)的时变可靠度,时变失效概率Pf(Ti,T)的记法同理.由图7可知,即使桥梁在20 a内能够通过较高强度的历史验证荷载而不失效,在随后的服役期可靠度下降的趋势仍然高于同期较低水平的历史验证荷载.这表明对结构进行预设的“历史荷载信息”强度不宜超过初始抗力的40%.若桥梁已服役20 a,且一年两遇的历史荷载记录与初始抗力比值接近40%,很可能亟需维修加固. 图7 基于验证荷载实验的结构时变可靠度Fig.7 Structural time-dependent reliability based on proof load testing 图8(a)和8(b)分别给出了γ由 0.001 a−1增大到 2 a−1时,不同强度的历史荷载对结构在20a的抗力均值µ(R20)和时变失效概率值Pf(20)的MCS结果.图例中,符号分别代表6个不同强度的“历史荷载”均值.由图可知:当作用于该桥梁的历史荷载均值低于6500 kN·m(初始抗力的31.6%),或γ<0.1 a−1时,对于 20 a结构的抗力提升效果不显著.因此对新建桥梁结构进行T1时刻之后的可靠性评估时,宜假定T0时刻荷载的频率大于等于一年两遇,年均增长率不低于 0.1 a−1;均值不低于R0的 31.6%.另外,当荷载均值分别为 7500 kN·m(初始抗力的 36.4%)和8000 kN·m 时,γ=1.5 a−1的Pf(20)分别为0.096和0.168,而γ=2 a−1的Pf(20)为0.116和0.197.这表明,在潮湿地区或沿海地区建造的钢筋混凝土桥梁,从抗力劣化算起,若频率为一年两遇的验证荷载的均值超过结构初始抗力的36%,且年均车流量增长率超过150%时,该桥梁在20 a内失效的概率较高,需要引起足够的重视,在设计、施工和服役时采取相应的措施. 图8 频率增大的多强度历史荷载对R20的验证结果及时变失效概率.(a) µ( R20);(b) Pf(20)Fig.8 Verification of R20 by multi-intensity historical loads with increasing frequencies and time-dependent failure probability: (a)µ(R20); (b) Pf(20) 图9 所示为λ=2 a−1,ε从 0 到 0.002 变化时采用式 (13)对应的结构在 0~40 a的时变失效概率Pf(T).由结果可知:式(13)可以考虑(0,T1)时段“历史荷载信息”的验证作用.当ε=0.002时的Pf(40)计算结果约为ε=0时的一半,可靠性显著提升,但需要与基于MCS的验证荷载实验结果对比. 图9 时变失效概率Fig.9 Time-dependent failure probability 图10给出了二者的对比结果.其中MCS对照组的频率函数为λ(t)=2+0.1t.由结果知,采用式(13)进行时变可靠度计算,结构在20~40 a的时变失效概率Pf(20,T)的范围介于6500 kN·m和7500 kN·m验证荷载实验得到的失效概率之间,这表明本文提出的计算方法具有很高的精度,对桥梁结构的可靠度评估效果更好. 图10 时变失效概率结果对比Fig.10 Comparison of time-dependent failure probability 图11以二次函数λ(t)为例,给出了MCS和式(7)计算得到的结构在20~40 a的时变失效概率.其中独立增量展示2个结果;关联增量展示1个结果.另外两个频率函数的结果十分接近,不再赘述.两种方法采用的历史荷载均值为6000 kN·m(初始抗力的29.1%). 图11 λ(t)为二次函数时公式 (7)与 MCS 的时变失效概率对比Fig.11 Comparison of time-dependent failure probabilities between Eq.(7) and MCS when λ(t) is quadratic 由结果可知,不论λ(t)的Gamma过程是增量独立还是增量关联的,时变失效概率结果都很接近,说明车辆荷载频率增量的关联性不影响结构时变可靠度的变化,因此上文中采用年均频率增量γ的方法是可行的.另外,MCS和式(7)得出结构的时变失效概率结果的差距随着λ(t)值的增大而增大,这说明一次修正后的车载发生次数较理论值仍然偏小,结果偏于安全.本例中,T=36~40 a的时变失效概率结果相差大于0.01,可以认为此时的评估模型不再适用;T=36 a对应的荷载频率最小值为 10.28 a−1.因此,当荷载频率λ>10 a−1,考察时段超过35 a,若验证荷载强度大于初始抗力的29.1%,式(7)不再适用. 本文基于Gamma随机过程和蒙特卡洛验证荷载实验提出了考虑车载频率非平稳增长的桥梁时变可靠度分析方法.另外,基于历史荷载对任意t (1)结构初始变异系数 ζ为0.15且服从对数正态分布时,若考虑 ζ为时间的函数 ζ(t),参数ε的取值宜小于0.002,或小于 ζ的1.33%. (2)“历史验证荷载”或真实历史荷载信息与初始抗力的比值对于结构后继服役期的安全性能评价至关重要.从结构劣化开始算起,若一年两遇的历史荷载值低于初始抗力的31.6%,且年平均增长率不大于 0.1 a−1,则荷载对 20 a 之内的抗力验证作用不显著,结构安全性能偏好. (3)建造在沿海地区和湿润地区的钢筋混凝土梁桥,从结构劣化算起,若频率大于一年两次的历史荷载均值超过结构初始抗力的36.4%,且车辆年均增长率超过150%,则该桥梁在20 a内的失效概率较高,需要引起足够重视,在设计、施工和服役时需采取相应的措施. (4)当ε≤ 0.002时,本文提出的抗力变异系数可变的公式具有更高的精度,评估效果更好. (5)采用本文提出的车载频率可变MCS方法得出的时变失效概率相较于实际计算结果偏于安全,可以在此基础上进行车载频数值的二次修正计算. (6)车辆荷载频率增量是否相关不影响结构时变可靠度的变化,结构可靠度计算中可以使用频率函数代替非平稳的频率增量.


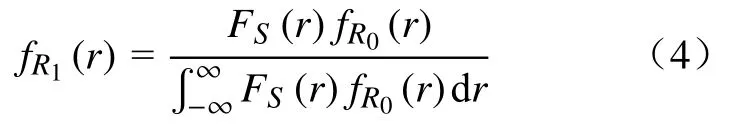

2 基于 Gamma 随机过程的频率函数 λ(t)


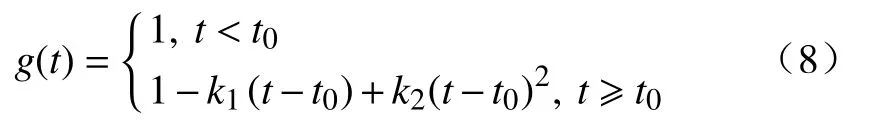


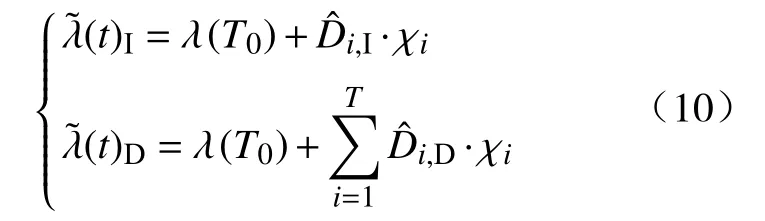


3 基于验证荷载的桥梁时变可靠度等效算法

4 实例分析

4.1 λ=2,ε取值范围讨论

4.2 频率函数 λ(t)=2+0.1t,验证荷载实验讨论

4.3 时变可靠度结果分析
4.4 频率函数基于 Gamma 过程的时变失效概率对比
5 结论
