基于有效应力的深锥泥层高度与底流浓度数学关系

2022-06-16那庆，王勇✉

工程科学学报 2022年7期

那庆，王勇✉

1) 北京科技大学土木与资源工程学院，北京 100083 2) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083

膏体充填是将废弃尾矿制备成膏体状料浆并通过管道输送到井下充填采空区，有效地解决了资源浪费、地表塌陷、尾矿坝环境污染等问题，成为当今矿业发展的主流方向[1−4].深锥浓密机作为膏体充填的关键设备在国内外也倍受青睐[5−6].深锥浓密机是通过上部泥层产生的压力和耙架转动将颗粒间的自由水排出，从而获得较高浓度的底流[7−8].众所周知，泥层高度越大底流浓度越高[9]，但在不同泥层高度情况下底流浓度的精准控制一直是研究难点.

目前，国内外学者对深锥浓密机泥层高度和底流浓度变化建立了大量预测模型，周旭等[10]进行了全尾砂絮凝动态沉降试验，并在考虑网络化泥层压缩屈服应力对脱水速度影响的基础上，建立了泥层高度、停留时间和底流浓度的预测模型.Wang等[11]利用机器学习中的XGBOOST建立了多个影响因素与底流浓度之间的关系，从而实现了对深锥浓密机底流浓度更全面的预测.Fang等[12]提出了一种基于注意力机制的神经网络（CNN）泥浆层高度预测方法，并进行相应实验证明了该方法的可行性和有效性.王勇等[13]将高径比定义为泥层高度与深锥直径的比值，并基于高径比建立了一种深锥浓密机底流浓度数学模型.吴爱祥等[14]以有效孔隙比与泥层压力的函数关系为基础，建立了深锥浓密机泥层高度与底流浓度数学模型，并从微观角度解释了该模型的变化规律.

也有学者关注到了提高底流浓度研究，王新民等[15]结合遗传算法建立了以深锥浓密机高度和锥角为输入，以底流浓度为输出的GA-SVM预测模型，并以司家营铁矿为例对深锥浓密机底流浓度进行预测优化.Du等[16]研究了超声波和机械耙共同作用对底流浓度变化的影响，研究发现，中等水平的超声波强度对底流浓度提高有一定促进作用.Jiao等[17]通过小型浓密装置，采用高精度CT扫描和三维重建技术，探索底流浓度的变化情况及孔隙结构演化.Hunter等[18]利用声学背散射系统对颗粒浓度进行剖面分析，分析两种耙架转速（0.1和1.1 rad·min−1）对浓度的影响.

综上所述，深锥泥层高度和底流浓度变化规律已有学者进行一定研究，但二者之间的内在关系却鲜有报道.此外，上述研究大多以实验为基础，对实验数据进行拟合回归来研究变量之间的相关性，以理论为基础的研究成果较少.为此，本文基于有效应力原理建立压缩系数 α分别为常数和变量时，深锥浓密机泥层高度与底流浓度数学模型，结合矿山实例对数学模型进行工业应用，分析两种数学模型之间的差异，探讨数学模型在动、静态压密过程中的适用性，以期为实际生产中深锥浓密机稳态运行的分析和设计提供理论方面的参考.

1 深锥浓密机中有效应力的应用

1.1 Terzaghi有效应力原理在深锥浓密机中的适用性

根据Terzaghi有效应力原理（简称有效应力原理），作用在饱和土体上的总应力由两种介质承担:一种是孔隙中的孔隙水压力，另一种是土颗粒形成的骨架上的有效应力[19].有效应力为单位截面上土体颗粒间所传递的荷载在某方向上分量的总和，土体的强度和变形主要由有效应力决定[20].由于孔隙水压力在各个方向上相等，又被称为中和应力.

有效应力原理的第一个前提条件为颗粒间的接触方式为点接触，即接触面可以忽略不计（接触面积比 αc=0），但在实际颗粒间接触面积比 αc≈0.03[21].不难发现，此时忽略接触面积比带来的误差就由孔隙水压力来决定.由式（1）可知，如果在深度为 1000 m 的海底，孔隙水压力u=10000 kPa，则αcu≈300 kPa，若海底某处泥层有效应力 σ′=100 kPa，αcu约为有效应力 σ′的3倍，显然颗粒间接触面积不可被忽略.但深锥浓密机的高度一般在20 m左右，产生的孔隙水压力与有效应力相近，忽略αcu带来的误差小于3%，因此颗粒间触面积可以忽略不计.

有效应力原理的第二个前提条件为颗粒间孔隙是连通的，且孔隙间的水为可以传递孔隙水压力的自由水.在浓密机动态压密（有耙架转动情况下）过程中，由于耙架旋转，稳定排列的颗粒结构被破坏，孔隙水沿着导水杆通道排出、尾矿浓度增加.在浓密机静态压密（无耙架转动情况下）过程中，尾矿颗粒依靠自身重力下沉，随着尾矿的堆积，底部尾矿受到的压力越来越大，孔隙中自由水被排出导致浓度增加.由此可知，无论在静态或者动态压密过程中，颗粒间孔隙水以可以流动的自由水为主，满足此前提条件，故有效应力原理适用于深锥浓密机泥层压力分析中.

由于尾矿浆在深锥压密过程中处于缓慢运动状态，一方面是由于耙架转动导致的“水平运动”，另一方面是由于上部低浓度尾矿浆加入和下部高浓度尾矿浆流出导致的“垂直运动”.故在此作进一步解释：（1）在动态搅拌中，耙架转速约0.05～0.1 rad·min−1，极为缓慢，假设某一瞬间耙架转动对内部泥层无扰动；（2）深锥浓密机在稳态运行过程中进料量与排料量相平衡，新进料浆停留时间一般在10 h以上，深锥浓密机高度一般小于20 m，则其垂直方向下降速度约为 0.56 mm·s−1，因此假设某一瞬间直壁部分稳定泥层均匀分布、无波动.

1.2 基于有效应力的尾矿浆受力分析

尾矿在深锥内沉降过程中颗粒经过自由沉降、干涉沉降和压缩沉降3个阶段，尾矿在深锥浓密机内部可以看作为“过饱和土体”，其沉降过程和受力分析如图1所示.

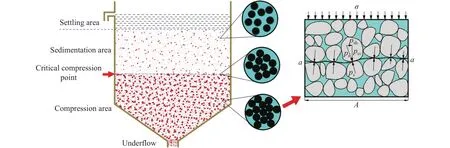
图1 深锥浓密机中尾矿颗粒沉降过程及受力分析示意图Fig.1 Diagram of the sedimentation process and stress analysis of tailings particles in a deep cone thickener

图1中假设深锥内饱和尾矿浆的横截面积为A，竖直方向上总应力为 σ，则总压力为 σA，截面aa为颗粒间各接触点连接形成的光滑曲线，颗粒间接触面积为Ac，接触点上的接触力Ps可分解为竖直方向力Psv和水平方向力Psh.由竖直方向上力的平衡可得到：

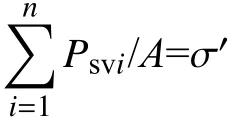
由于深锥内尾矿颗粒间为点接触，故接触面积比 αc约等于0.由此可得到有效应力 σ′的表达式为：

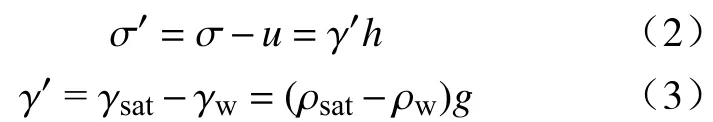
其中，γ′为尾矿颗粒浮容重，kN·m−3； γsat为尾矿颗粒饱和容重，kN·m−3； γw为水的容重，kN·m−3； ρsat为尾矿浆饱和密度，kg·m−3.

2 深锥浓密机泥层高度与底流浓度数学模型

2.1 压缩系数 α与泥层压力的关系

压缩系数 α可以由侧限压缩实验得到，用来表征颗粒在不同载荷和完全侧限条件下的变形特性[22].相似地，在深锥浓密机中，由于上部泥层压力增加，颗粒重新排列、孔隙由小粒径颗粒充填，孔隙比逐渐减小，下部泥层越来越密实.孔隙比与载荷呈一一对应关系，压缩系数 α的计算公式为[18]：

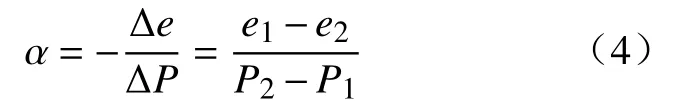
其中，α为压缩系数，MPa−1；e1、e2为压缩前后颗粒达到稳定的孔隙比； Δe为压缩前后孔隙比增量；P1、P2为压缩前后所需的压力，MPa； ΔP为压缩前后压力增量，MPa.

2.2 临界压缩浓度的确定

根据图1所示，在自由沉降过程中，尾矿颗粒保持初始入料浓度等速下沉，颗粒浓度达到一定值后，颗粒之间会相互影响，这种相互影响与渗透力j有关（j=γwξ，ξ为水力梯度），有固体颗粒下沉就有同等体积的水上升，上升的水流对颗粒产生向上的摇曳作用阻碍颗粒沉降，导致颗粒沉降速度降低，随即进入干涉沉降阶段.随着颗粒浓度持续增加，颗粒之间开始接触，干涉沉降结束，但此时颗粒间无力的传递，有效应力 σ′为0.在上部压力作用下颗粒开始挤压，进入压缩沉降阶段.在干涉沉降结束和压缩沉降开始的交叉点称为临界压缩点，对应的浓度为临界压缩浓度c0.

根据临界压缩点定义可知，临界压缩点处颗粒间为点接触，并且颗粒间无应力传递.由此，临界压缩点处孔隙比约等于颗粒最松散时孔隙比，临界压缩浓度c0可根据式（7）求出.

临界压缩浓度c0也可以通过静态沉降实验确定，绘制界面高度与沉降时间关系曲线，得到临界压缩点高度后，根据式（5）确定临界压缩浓度：

其中，c0为尾矿临界压缩浓度，%；cin为初始入料浓度，%；Hin为初始液面高度，cm；H0为临界压缩点高度，cm.

2.3 a为常数时泥层高度与底流浓度关系

当尾矿颗粒进入临界压缩点后开始出现泥层堆积，泥层高度则为某一泥层面到临界压缩点的垂直距离.在临界压缩点处建立泥层高度H与浓密机半径R的直角坐标系，如图2所示.

图2 基于临界压缩点建立的泥层高度与浓密机半径直角坐标系Fig.2 Rectangular coordinate system of mud height and thickener radius based on the critical compression point

由图2可知，P为h厚度的泥层产生的有效应力，c为距离临界压缩点h处泥层的平均浓度（简称泥层浓度），其中dc的表达式为：

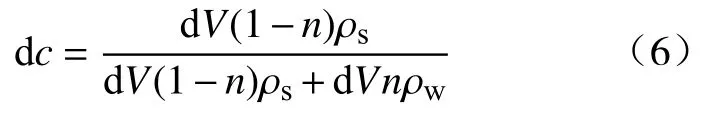
其中，dc为dh泥层平均浓度，%；dV为dh泥层体积，dV=πR2dh，m3；n为该泥层孔隙率，n=e/(1+e)，%.根据式（6）还可推导出孔隙比与浓度关系式为：

其中，e为该泥层孔隙比；Gs为颗粒比重，Gs=ρs/ρw.由有效应力原理可知dh泥层产生的有效应力dP为：

其中，ρsat为深锥浓密机中不同泥层高度下尾矿浆饱和密度，g·cm−3.值得注意的是： ρsat并不是定值，从深锥浓密机上部到底部，随着泥层高度增加，尾矿颗粒不断被压实，ρsat逐渐变大.单位体积泥层中，泥层浓度越大表明尾矿颗粒含量越高，泥层密度越大，由此泥层浓度和密度存在的对应关系为：

当尾矿颗粒进入稳定压缩阶段后压缩系数α可视为常数[23]，式（4）可变为：

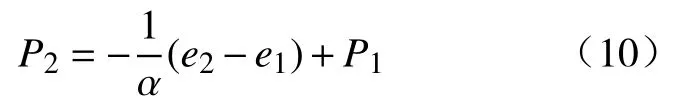
由式（10）可知，当P1等于 0时，e1=e0为常数，则dP还可以写成：

将式（8）和式（11）联立可得到：

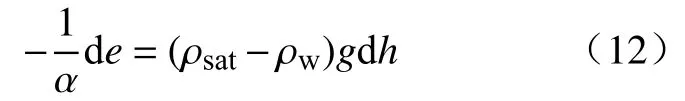
将式（7）和式（9）代入式（12）中有：

对式（13）两边同时积分得到泥层高度与底流浓度关系为：

其中，D1为积分常数，将边界条件：在临界压缩点处h=0、c=c0代入式（14）中求得D1：

得到常数D1后原式（14）可以写成：

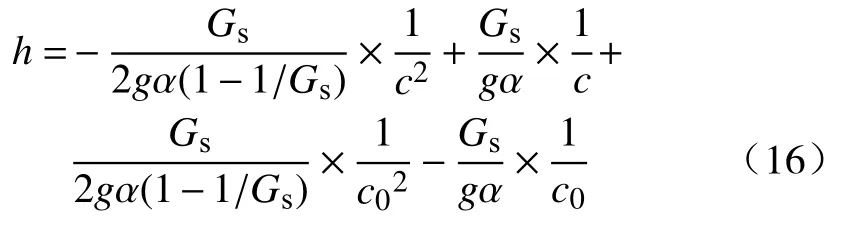
对于特定尾矿颗粒而言，Gs、c0均为可确定的常数，压缩系数 α由最大泥层高度和对应底流浓度代入式（16）确定.由于式（16）过于繁琐，故可简化为：

式（17）中，A、B均为大于 0的常数，A=Gs/2gα(1−1/Gs)，B=Gs/gα.式（17）从理论的角度揭示了压缩系数 α为常数时泥层高度和底流浓度的关系.

2.4 α为变量时泥层高度与底流浓度关系

在侧限压缩实验中，压缩系数 α是一个与孔隙比有关的变量，随着孔隙比逐渐减小，颗粒被压实越来越困难.方永伦等[24]利用最小二乘法拟合回归出孔隙比与压缩系数之间的关系：

将式（18）代入到式（13）中有：

式（19）中：k为修正系数，由于颗粒的压缩性与颗粒密度、粒径等有关，不同颗粒压缩系数不同，故引入修正系数k来减小计算误差.值得注意的是，对于特定浓密机处理特定尾矿而言k是一个常数，当深锥稳定运行时，将最大泥层高度和对应的深锥底流浓度代入式（21）中求出k值.式（19）中的e也可以由式（7）代替，代入后可得到底流浓度c与泥层高度h之间的关系式：

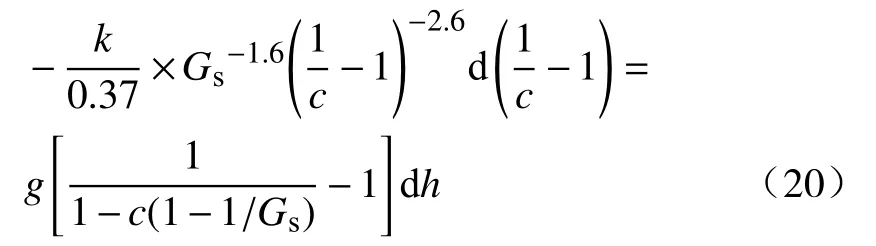
等式两边同时积分可得到：

其中，D2为积分常数，代入h=0时c=c0约束条件后，同样地也可将式（21）简化为：

其中，M、N均为大于0的常数，M=kGs−1.6/0.37g，N=1−1/Gs，D2=−M(1/N−1)(1/c0−1)−1.6/1.6−M(1/c0−1)−0.6/0.6N，式（22）从理论的角度揭示了压缩系数为变量时泥层高度和底流浓度的关系.该数学模型物理意义：不同泥层高度下，产生的有效应力不同，颗粒间孔隙率不同.随着上部泥层高度增加，底部尾矿颗粒受压重新排列组合，孔隙间的水被排出，颗粒被压缩的越密实.即泥层高度越大，颗粒间孔隙率越小，底流浓度越高.

3 数学模型在工程中的应用

3.1 某矿深锥泥层高度与底流浓度数学模型构建

某矿山深锥浓密机直径为18 m，总高为16.7 m，锥角为30°，扭矩为2.7×106N·m，处理能力为5000 t·d−1，最大底流流量为 265 m3·h−1，底流浓度为 70%.尾矿基本物理性质如表1所示.

表1 尾矿物理性质参数表Table 1 Physical property parameters of tailings

由表1可知尾矿松散孔隙率n=66.28%，根据式（7）可算出临界压缩浓度c0=60.18%.浓密机最大泥层高度hm=16.7−3=13.7 m（根据工程经验，认为最小澄清区高度为3 m），将上述参数代入式（16）、式（22）中求得数学模型中关键参数如表2所示，进一步得到两种情况下数学模型的表达式分别为：

表2 数学模型关键参数表Table 2 Key parameters of the mathematical model

式（23）为 α为常数时泥层高度h1与底流浓度c的关系式h1=f1(c)，式（24）为 α为变量时泥层高度h2与底流浓度c关系式h2=f2(c).绘制泥层高度与底流浓度关系曲线如图3所示.

图3 泥层高度与底流浓度关系曲线Fig.3 Curves of the relationship between mud height and underflow concentration

由图3可知，上述两个数学模型中泥层高度与底流浓度均呈幂函数关系，并且随着泥层高度增加，底流浓度逐渐增大；底流浓度达到70%前，同浓度下h1大于h2，底流浓度达到70%之后，同浓度下h1小于h2，引起该差异原因在后文进行分析；在h2=f2(c)数学模型中，随着浓度增加，泥层高度变化引起底流浓度的变化越来越小.例如：底流浓度从60%增加到65%所需要的泥层高度为5.79 m，底流浓度从70%增加到75%所需要的泥层高度为11.22 m，后者所需要的泥层高度约为前者的1.94倍.在实际生产中浓密机高度对底流浓度影响固然重要，但一味的通过增加泥层高度获得更高的底流浓度可能“事倍功半”.

3.2 两种模型对比分析

对式（23）、（24）求导，得到一阶导函数与底流浓度关系曲线，如图4所示.图4中dh/dc为泥层高度变化率，dh/dc越大说明进一步被压缩所需的泥层高度越大.由式（4）可知，压缩系数 α与压力成反比，α越小说明颗粒越不容易被压缩，增加相同浓度需要更大的泥层高度，故猜测 α大小关系为引起两个数学模型差异的主要原因.为验证这一观点，基于式（24）推导 α与c的关系为：

图4 压缩系数、dh/dc 与底流浓度关系曲线Fig.4 Curves of the relationship between compressibility, dh/dc, and underflow concentration

根据式（25）绘制 α与c的关系曲线如图4所示，图4中 α1、α2分别为h1=f1(c)、h2=f2(c)中的压缩系数值.由于 α1为常数、α2随浓度增加逐渐减小，底流浓度在60.18%～65.13%内、α1小于 α2；当底流浓度超过65.13%时、α1大于 α2，与上述观点相符.值得注意的是，此数学模型中计算得到的压缩系数较其他土体压缩系数大，可能的原因是矿物颗粒较土颗粒粒径大，所以孔隙所占体积更大、更容易被压缩；另一个原因可能是深锥浓密机中泥层受力压缩并不是严格意义上的压缩实验，浓密机中条件更为复杂，所以得到的压缩系数与压缩实验结果有差异.

4 模型适用性分析及泥层区域划分

4.1 模型在动、静态压密过程中的适用性分析

由上述分析可知，有效应力原理在动、静态压密过程中均适用，但基于有效应力原理建立的泥层高度与底流浓度数学模型在动、静态深锥压密过程中适用性需进一步分析.在实际生产过程中，动态压密由于耙架转动，压密效果优于静态压密，即相同条件下动态压密底流浓度高于静态压密底流浓度[25].但根据式（23）、（24）可知，无论在动态或者静态深锥浓密过程中，只要泥层高度相同，就会产生相同的底流浓度，那么数学模型与实际情况产生“矛盾”？

一方面，是由于两种压密状态作用机理不同，动态压密中耙架转动会破坏絮团受力平衡，使得絮团破坏、内部水分沿导水杆流出，浓度增加程度高于无耙架情况；另一方面，所谓的“泥层高度相同”是指临界压缩点到深锥底部距离相同，但其泥层内部尾矿浓度及浓度分布不同，导致泥层产生有效应力不同，进而对深锥内尾矿压缩程度也不同，反应在数学模型中的差异则为压缩系数 α、修正系数k的不同.即泥层高度相同情况下，动态压密过程中底部浓度更大，则 α更大或者k更小.因此，该数学模型对于动、静态压密情况均适用，而且并无“矛盾”.值得注意的是，动、静态压密不能一概而论，需分别计算函数表达式建立泥层高度与底流浓度的关系.