注重过程探究 构建有效课堂

文/洪建章

引言

学生学习知识，从理解到掌握再到应用需要一个过程。知识自身也有一个发生、发展和应用的过程。因此，教师不仅要明确知识生成的过程，还要明确教材中练习设置的变化和延伸过程，为学生提供独立探索的机会。笔者认为，在数学课堂教学中应注重过程探究，使学生对数学产生兴趣，激发学生学习的积极性，培养学生掌握知识、运用知识的态度和能力，构建高效的数学课堂。

一、注重知识形成过程探究

问题驱动指引贯穿了学生的数学学习过程。序列问题有助于引导学生了解知识的来龙去脉，经历知识的发展过程，从而形成对概念、原理等的深刻理解。对过程中蕴含的数学思想的体会与感悟，有助于发展学生的问题意识、探索精神。学生在学习中不仅要知道知识“是什么”，更要清楚“为什么”和“怎么样”。其中，了解“为什么”和“怎么样”就体现了对知识逻辑形式的探究。经过这种过程性的探究，学生能够逐渐明了知识涉及的思维结构和思维方法，将客观的符号知识内化为个人的认知结构，实现“转知成智”。在教学中，教师要精心设计探究过程，体现知识的形成过程，让学生深入理解知识，在运用知识时得心应手，使数学课堂教学更加有效。

例如，在“有理数的乘方”一节中，乘方的意义及求有理数的正整数指数幂是重点和难点，正确理解底数、指数和幂的概念，是正确运算解答乘方的关键。对此，笔者在教学过程中设计了三组问题，由浅入深，让学生通过比较、辨析来理解概念，真正体会幂的运算由来，注重知识的形成过程，真正理解幂的概念。

问题1：把下列各式用乘方的形式表示。

（1）2×2×2×2×2×2=____；

问题2：

（1）在94中，底数是____，指数是____，表示的意义是____________________________；

（2）在（-5）3中，底数是____，指数是____，表示的意义是____________________________。

问题3：53与35的意义相同吗？与的意义相同吗？为什么？

注重知识形成的过程，一方面是新课中的知识形成过程，要理解知识的来龙去脉；另一方面是知识体系形成的过程，要理解知识间的区别与联系[1]。学生在理解的基础上才能形成结构化的知识，在综合背景的问题中，才能选择和调用相应的知识，这样的数学课堂教学才会更高效。

二、注重解题过程探究

数学习题中有很多极具教学价值的问题，在教学中教师不能仅仅就题论题，给出结果或答案即可，而应充分挖掘题目中的丰富内涵。深度教学要注重学生在教学过程中的切身体会、感受与经验，丰富学生的过程体验。这是深度教学的要求，也是对学生学习过程性的回应。因此，教师在教学中应尽量让学生参与到解题过程探究中，让学生真正体会习题中包含的知识，快乐地探究学习，使学生不断完善知识结构和认知结构，培养学生举一反三、触类旁通的能力[2]。

以“实际问题与二次函数”这一节的一道习题为例：已知飞机着陆后滑行的距离s（单位：m）关于滑行的时间t（单位：s）的函数解析式是s=60t-1.5t2，求飞机着陆后滑行多远才能停下来？在讲解此习题时，笔者设计了如下的探究过程。

甲同学：准备一架模型飞机，用教室地板当跑道，演示飞机滑行的过程。

乙同学：在黑板上，先建立直角坐标系，t轴表示时间，s轴表示飞机滑行的距离。随着甲同学的演示过程，在直角坐标系中把图像画出来，如图1所示。

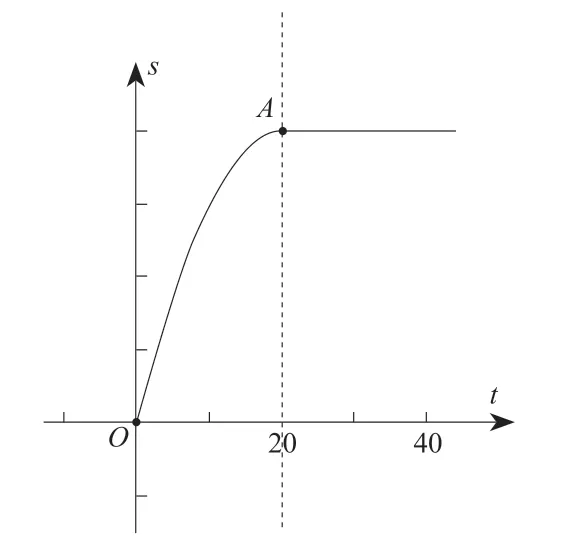
图1

在这样的探究过程中，学生真正理解了随着时间t的增加，飞机滑行的距离s从只有增加不会减少到最终不变的事实，明白了点A的含义，体会了二次函数与实际问题的联系，达到了对知识的真正理解和应用。

又如，地面上一个小球被推开后开始滑行，滑行的距离s与时间t的函数关系如图2 中的抛物线所示（A是抛物线的顶点），则下列说法正确的是（ ）。

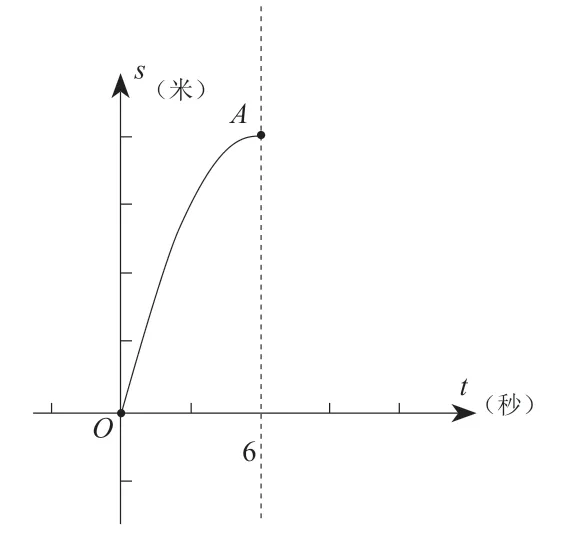
图2

A.小球滑行6 秒停止

B.小球滑行12 秒停止

C.小球滑行6 秒回到起点

D.小球滑行12 秒回到起点

三、注重知识的重现过程探究

《义务教育数学课程标准（2022年版）》指出，课程内容不仅包括数学的结果，还包括数学结果的形成过程和蕴含的思想方法。对此，教师要重视学生的参与过程，重视知识的重现过程。

例如，在“点和圆的位置关系”这一节中，教师在讲解如何确定外接圆的圆心时，可设计如下问题：

问题1：给出一个圆形（大于半圆）纸片，如何确定圆心，并把残缺的部分补完整？方法1：在纸上用折叠法尝试，确定圆心，补完图形，如图3所示。方法2：利用三角板中的直角及圆周角的性质，如图4所示。

图3

图4

问题2：撕碎圆形纸片，给碎片定圆心。教师将圆形纸片当着学生的面撕碎(可多撕几下)，为学生设置一个新的情景：如何确定一块碎片所在圆的圆心呢？

学生可以利用“过不在同一条直线上的三个点确定一个圆”，即利用外心的性质作圆，找出圆心，补完图形（如图5）。

图5

知识的再现过程有助于学生了解所学知识从何而来、解决何种问题、怎么解决，在有限的时间内探究知识[3]。这样学生不是被动地接受知识，而是主动获取知识，获得真正意义上的学习能力。同时，整个课时也收到了良好的教学效果。可见，有了学生的参与，再现知识过程的探究，课堂教学才会生机勃勃，学生才会成为课堂学习的主体。

四、注重思维过程探究

完整的思维过程包括审题、解题、反思。教师要创造机会让学生经历完整的思维过程，让学生理解数学思维方法、解决问题的策略。教师的主导作用应该体现在选择好的题目、设计好的问题，以及提炼可推广的方法、策略或技巧[4]。

以下面一题为例：“若抛物线y=x2+bx（b＞2）上存在关于直线成轴对称的两个点，则b的取值范围是________。”此题考查二次函数与不等式二次函数与一元二次方程的关系、轴对称的性质、因式分解等知识点。对此，教师可以设计如下探究过程：

问题1：如果点A、点B是关于直线成轴对称的两个点，它们有什么特点？（引导学生根据性质设点A（m，n）、点B（n，m））

问题2：点A、点B与抛物线y=x2+bx有什么关系？（引导学生利用待定系数法解决，思路进一步打开）

由（1）-（2）：得n= -b-1-m

代入（1）：得到关于m的一元二次方程：

m2+（b+1）m+（b+1）=0

问题3：存在性与一元二次方程的根有什么关系？（引导学生与一元二次方程根的判别式联系起来，思路更近一步，慢慢感觉豁然开朗）

Δ=（b+1）2-4（b+1）＞0

即：b2-2b-3＞0

问题4：想一想二次函数图像与不等式的关系。

此时，令p=b2-2b-3。教师引导学生画出图像（如图6）。

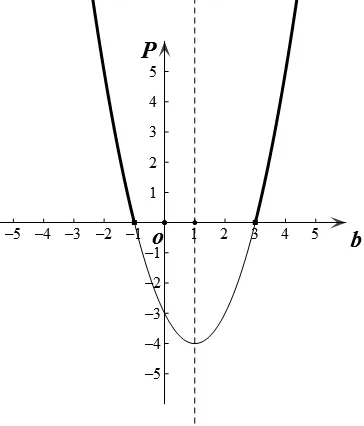
图6

∵b2-2b-3＞0（即p＞0）

∴b＜-1 或b＞3

又∵b＞2

∴b＞3

注重思维过程探究，可以让学生真正经历完整的思维过程，使学生参与审题、析题、解题的探究过程，有利于学生理解数学思维方法，利用数学思想方法找到解决实际问题的策略、技巧，使学习更有效。

结语

正如布鲁纳所说，“探索是教学的生命线”，这条生命线就是一个个大大小小的过程的集合。在数学课堂教学中，教师要注重知识形成过程探究，注重解题过程探究，注重知识的重现过程探究，注重思维过程探究，使学生更深入地理解知识、掌握知识，真正学会解决问题的方法。