基于特征选择和降维的心音信号识别的研究*
2022-06-16李海霞朱慧博张施琴毛凌锋
李海霞 朱慧博 张施琴 毛凌锋
(1.宿迁学院 宿迁 223800)(2.北京科技大学 北京 100083)
1 引言
心脏病是严重威胁人类健康和生命的主要疾病之一。心音信号是人体重要的生理信号之一,蕴含了人体大量的心脏原始病理信息。它来自于人体内部的信号,不容易被模仿或复制[1]。目前,国内外有许多针对心音的检测和识别方法,这些方法都需要准确提取心音的各项特征参数。Taikang Ning等通过能量和频率等特征,实现对心音的快速分类[2]。李天生通过使用经验模态分解、希伯特-黄变换等方法,从多个角度提取了多种心音特征信号,进而完成心音的识别[3]。
为了提高识别率,人们采用了很多方法。王建卫等[4]利用图像处理技术进行心音信号的识别;李战明等[5]利用S 变换提取心音信号特征,用于不同类型心音信号识别;Olmez 等[6]利用小波变换提取心音信号的时、频域特征参数,对7 种不同心音信号进行分类识别,识别率达99%,但ANNs 的频域计算繁琐,计算量大,识别过程运算时间过长;成谢锋等[7]将一维心音信号转换成二维心音图,采用图像处理技术提取心音的图像特征,但需要将一维信号变为二维,增加了计算量。Rios-Gutierrez等[8]采用离散小波变换及短时时频变换方法提取心音信号特征参数,再借助矢量化(Vector Quanti-zation,VQ)模型对4 种常见心杂音分类识别,但识别率仅有67.05%。
本文选择了郭兴明等[9]使用的小波包分解和周静等[10]使用的功率谱估计这两种方法,计算得到心音参数,依据特征选择对两种不同方法得到的多个参数进行筛选和验证,从而找出能较好反映心音本质特征且具有差异性的参数。然后,再将特征选择得到的参数进行进一步降维处理,用于节约计算成本。整个实验过程既剔除了无关参数对心音识别的干扰,又减少了投入训练和识别的参数个数,使得在大规模样本数据处理时能够更高效,还进一步提高了心音信号的识别率。本文研究成果表明,基于特征选择后降维处理的心音识别具有高效性和可行性,拥有一定的推广应用前景。
2 基本理论和方法
本文采用层级式的信号识别流程,先对心音信号进行特征提取,然后对多维心音特征进行筛选,通过心音识别率验证不同方法在心音分类中的效率。在特征选择层中,本文选择了3 种特征选择方法,同时设置了1 组随机选择作为对照组,以最后的识别结果成功率作为验证方法,逐个观察几种特征选择方法对心音特征的筛选效果。将特征选择效果最好的一组结果作为降维的输入。在降维层,同样设置主成分分析法和线性判别分析法互为对照,通过结果验证得到最优方法。具体步骤如图1所示。
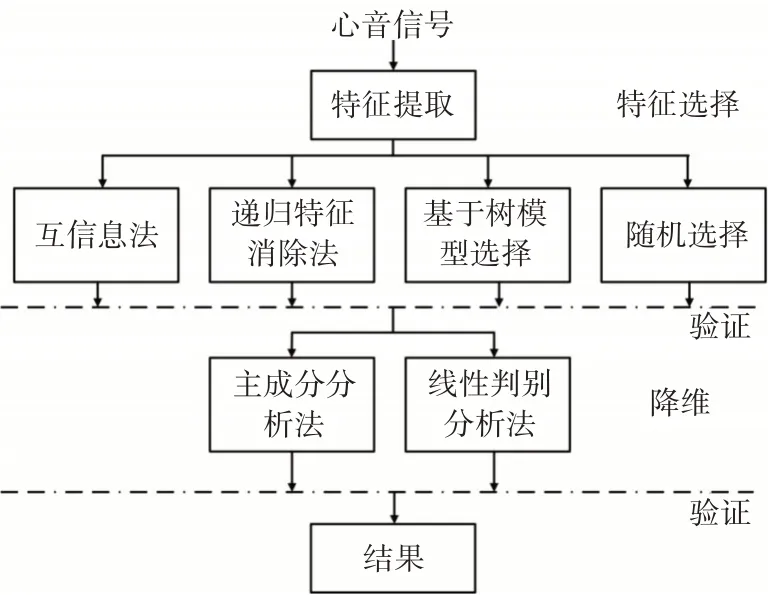
图1 整体实验流程
2.1 特征提取及验证方法
本文对10 种不同心音信号在已获得心音周期的前提下对其提取特征值[11~12],其中,通过小波包分解提取参数16 个,分别是3 次小波包分解后的8个频带分量所占的百分比和8 个频带能量占比;通过功率谱估计得出的最低频段、次低频段、次高频段、最高频段在信号中的占比、信号的平均分贝及信号在最高分贝处的赫兹。
2.1.1 小波包特征提取
小波变换是从短时傅里叶变换中发展而来,可以实现对信号内任意频段的聚焦。图2 为小波包分解模型,每层都将上层的频带再次细分为低频分量A 和高频分量D 两个频段。因为小波包可以将信号连续分成多个等宽频带,使其对没有被细分的高频部分得到再次分解,从而克服了高频段其频率分辨率较差,在低频段时间分辨率较差的问题,在处理复杂的心音信号时,能较为详尽地描述心音的细节变化,具有一定的优势。

图2 小波包分解示意图
小波包分解的迭代算法为

式 中,di,j,m为 第j 层 第m 个节点的第i个小波包系数;h(k)和g(k)分别为多分辨率分析中正交镜像滤波器的低通和高通滤波器系数。
功率谱是表示频带内信号功率随频率的分布情况,而功率谱估计是根据有限数据在频域内提取被淹没在噪声中的有用信号。对于平稳随机信号,难以通过数学关系来描述信号的具体状态,只能根据有限的数据大致估算出它的功率谱密度。
图3 为一例正常心音周期波形和一例二尖瓣关闭不全心音周期求得的功率谱估计结果,根据此结果可以对不同频率段的功率量占比进行划分,从而求得功率谱相关的特征值。
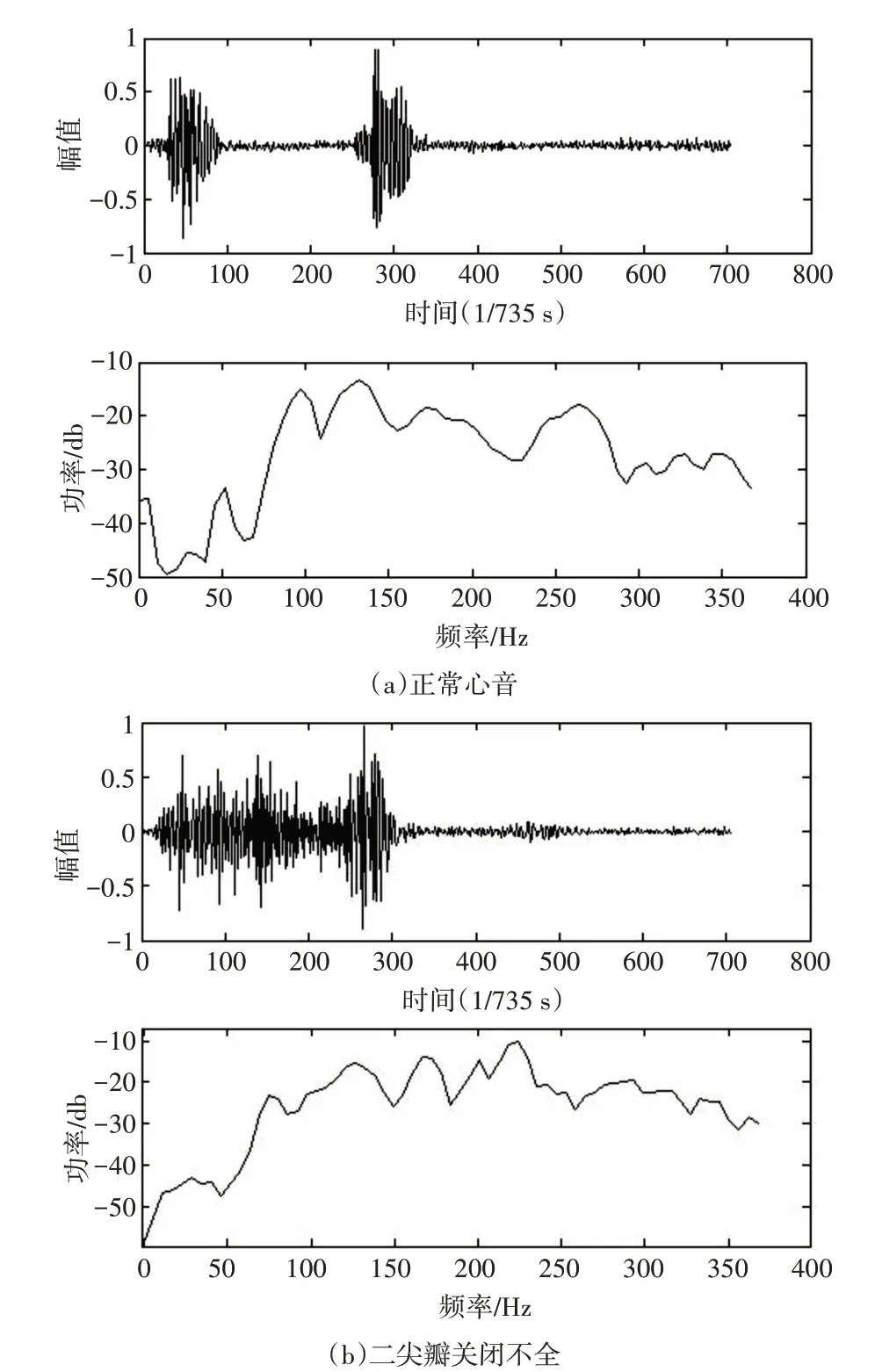
图3 心音波形及其功率谱估计结果
2.1.2 验证方法
概率神经网络具有较好的鲁棒性和容错性,能在一定的范围内允许同一特征点的特征值存在误差[13]。它基于贝叶斯最优分类决策理论和概率密度估计算法,学习过程简单,能够通过概率竞争得出唯一结果。与BP 神经网络相比,不会陷入局部极小值,被广泛应用于模式识别和模式分类领域。对心音的分类需要具体的结果,所以通过概率神经网络对特征参数进行识别,逐一验证不同的特征选择和降维方法对心音信号的特征参数的分析结果。每种心音类型选取3 例作为训练样本,训练得到神经网络后对所有样本进行识别,以此获得识别率。
2.2 特征选择算法
根据不同选择形式,特征选择大体可分为3 种类型:过滤法(Filter)、包装法(Wrappe)、嵌入法(Embedded),本文将分别使用3 个不同的模型,对心音特征进行选择。在选择过程中,同验证方法一样,每种心音信号选取3 例进行特征选择。这三种模型使用的算法分别如下。
1)互信息法
互信息(mutual information)是用来评价一个事件的出现对于另一个事件的出现所贡献的信息量。在特征选择中,需要每个特征所蕴含的信息相对独立,尽量少的与其他特征相互重合。通过特征间互信息计算进行升序排序,筛选出互信息量低,能较好描述心音信号特征的参数。
2)递归特征消除法
递归特征消除法是一种寻找最优特征子集的贪心算法。本文选择了基于逻辑回归(Logistic Regression)的递归特征消除法,其作用是反复构建逻辑回归模型,然后根据系数筛除相对较差的参数类别,然后再在筛除后的特征集上重复这个过程,从而保留最好的特征参数。
3)基于树模型的特征选择
本文选择了迭代决策树[14~15](Gradient Boosting Decision Tree,GBDT)模型来实现心音特征的选择,它是一种机器学习模型,其优势在于通过多棵树来共同决策,从而输出特征权重较为突出的参数类型。
2.3 降维
降维与特征选择的不同点在于,特征选择只筛选出能够反映样本特征,更具有差异化的参数,而不改变参数的值;降维的本质是将参数由高维度空间映射到低维度空间,在尽量保存原有参数特性的情况下,减少参数数量,因此参数的值将不再是原本的特征值。
主成分分析法(Principal Component Analysis)是一种无监督的降维方法,它使得样本特征具有较大的发散性,使得样本特征能够适应更多的实例,而线性判别分析法(Linear Discriminant Analysis)是一种监督式的降维方法,在映射后,特征样本一定程度地损失了发散性但具有最佳的分类性能[16~17]。
主成分分析流程图如图4所示。

图4 主成分分析流程图
3 结果与分析
3.1 特征提取的验证结果
表1 是10 种心音计算得到部分特征参数的样本均值,其中AAA3 频带分量和DDD3 频带分量由小波包计算得到。功率谱最低频段占比、功率谱最高频段占比、功率谱信号平均功率由Welch 谱估计方法得到。
在表1 中,可以看出室间隔缺损的识别成功率明显低于其他心音信号的成功率,并且大幅降低了整个心音样本的识别率。在识别错误的17 个样本中,有7个被误识别为二尖瓣关闭不全,有6个被认为是主动脉回流,4 个被误识别为动脉导管未闭。而从表中数据可知,室间隔缺损的DDD3 频带分量明显高于二尖瓣关闭不全和主动脉回流,其功率谱最高频段占比也明显区分于动脉导管未闭,识别率低的原因是由于其他特征混淆。因此,对多维特征的心音样本进行特征选择是必要的。
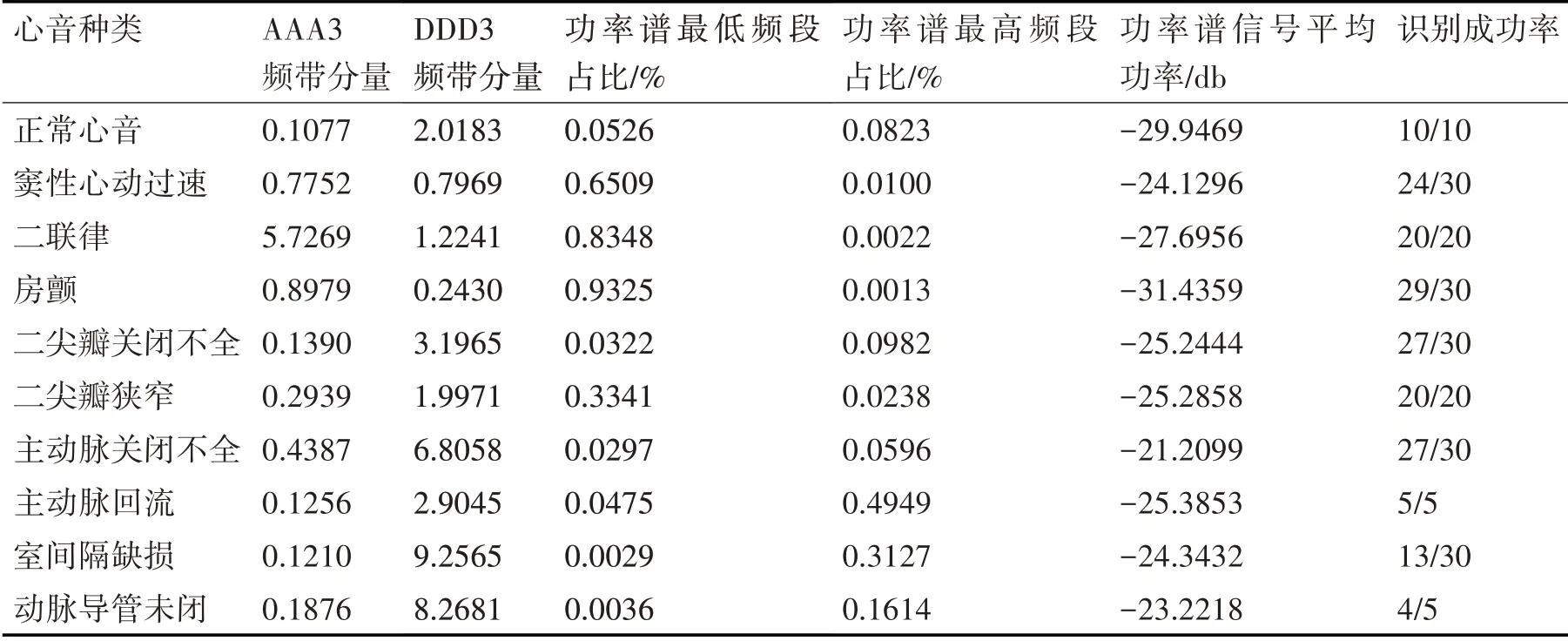
表1 不同种心音的部分特征参数(样本均值)及其原始数据识别成功率
3.2 不同特征选择方法的验证结果
根据对心音特征样本多次的实验,选取不同特征个数作为识别验证的训练集和识别集,最终选取参数数量及识别成功率结果如表2所示。
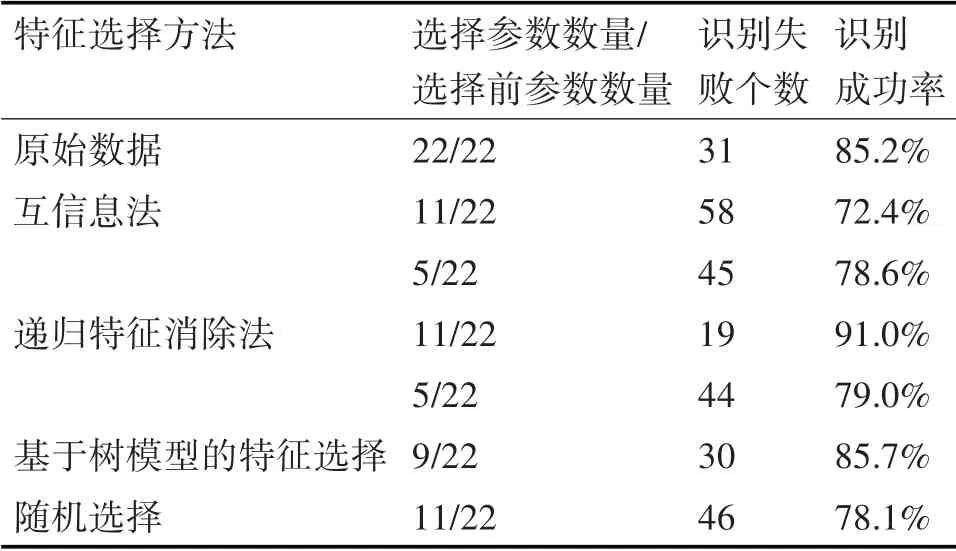
表2 不同特征选择方法的验证结果
由表2 可以看出,在22 个特征选择中,直接选择其中5 个参数,筛选了大量有效心音信息,而使得识别率不可靠。基于树模型的特征选择利用递归模型自动选择了9 个心音参数,但并未明显提高识别率。而在筛选出11 个参数中,递归特征消除法实现的心音识别率最高,且较原始数据有明显提升。
这一结果表明其选择结果有效地剔除了干扰项参数对结果的影响,选择出更能表现出心音特征的心音参数。
3.3 降维验证结果
将在3.2递归特征消除法中得到的参数分别用主成分分析法和线性判别分析法进行降维处理,将11个参数降为5个,其识别成功率如表3所示。

表3 不同降维方法的验证结果
降维的目的是进一步减少参数个数,当样本数据过大时,能有效降低计算量,简化训练和识别的过程。表3 的数据显示,本次实验中,两种降维方法都在减少了参数数量的同时,一定程度上提高了心音识别的成功率,且主成分分析法的识别成功率达到92.9%。
4 结语
本文提出的对心音信号先特征选择再降维的的识别模型,通过对210 例样本的试验分析,结论如下。
1)在对22 个心音特征参数的选择中,利用递归特征消除法选择11 种参数达到了较好的结果,与原始数据相比,识别率上升明显,可以以此进行数据降维。
2)在对数据降维的过程中,主成分分析法和线性判别分析法均得到较好的识别率。可见,在多维心音识别中,进行数据选择和降维是必要和有效的。
3)本文所提心音识别方法能有效提高心音分类识别准确率,可以结合更多特征参数及时域特征进行分析,对进一步实现心脏疾病诊断具有重要参考价值。
