基于税收预测的层级时序记忆算法研究*

冯晓钰 刘亮亮 张再跃 张晓如

（1.江苏科技大学计算机科学与工程学院 镇江 212003）（2.上海对外经贸大学统计与信息学院 上海 201620）

1 引言

税收是筹集财政资金的重要途径之一，宏观意义上可以调节经济，起到反应与监督的作用。税收预测的研究也已逐渐成为寻找我国经济发展方向的方法途径之一，税收预测的标准和要求同样随着技术的提高不断严格［1］。因此，利用两种预测模型来分析影响我国税收收入的主要因素［2］，而后研究税收影响因素的作用机理，并确定主要因素的影响程度，建立系统的税收预测模型体系，客观准确地预测某市的中期税收收入。

很多国内外学者在预测税收收入时聚焦于影响税收收入的因素，事实证明经济发展水平、税收政策以及物价水平都是影响税收收入的因素。然而，很多预测方法受到样本数据分布以及样本容量的限制。

历年以支持向量机和BP 神经网络［3］两种方法建立模型在税收预测上取得了明显的进步。Rumelhart 等提出了BP 神经网络模型，以及Vapnik［4］等提出的支持向量机，对税收预测的研究有一定的实质性进展。近年来，由Numenta 开发的新学习型预测算法（层级时序记忆算法，HTM），HTM 学习算法并不局限于特定的应用领域，所以可以用于税收数据预测这一方面的研究。本文着重采用层级时序记忆算法进行建模［5］，研究了某市税收预测模型，并采用历年税收收入数据验证了模型的有效性与实用性，与基于支持向量机的税收预测模型进行预测结果对比分析。

2 层级时序记忆算法（HTM）的基本原理

2.1 HTM的基本思想

层级时序记忆算法（HTM）是机器学习算法，其模拟新大脑皮质功能和结构的神经形态，具有稀疏、层级和模块化这三个特点，通过稀疏分布表示、空间池与时间池，完成学习任务［6］。HTM 网络结构如图1 所示。按照层级排序的区域组成一个HTM网络，其中的区域［7］是由一层成列的高度内联的细胞而组成。每一个区域都注重寻找一起出现的输入位组合，通过从感官数据中发现模式或者模式序列来了解自己的区域唯一的激活方式，从而形成空间模式，接着去学习空间模式如何随时间变化，从而找到时序模式。当HTM 学习模式完成后，它就可以对新输入进行识别。若HTM 接收到输入时，它会与之前学习到的空间和时序模型进行匹配。

图1 HTM网络结构

由此，细胞活跃是一个细胞会与前一时刻活跃的细胞建立连接的前提，然后细胞可以通过加强细胞之间的连接来预测自身何时会被激活。HTM 的区域不存在专门用于存储模式序列的存储中心，而是将记忆离散地存储在单个细胞内。系统因离散存储而具有很强的健壮性，单个细胞出现失效或无法正常工作的问题，对于整个网络往往不构成较大影响。

2.2 HTM模型建立

HTM 时间池识别输入数据的时序模式［8］，将情景因素加入表征和预测。HTM 时间池模型如图2所示。一个细胞以数十个树突区域和数千个突触来识别成百的独立的细胞活跃状态。因为模式是巨大且稀疏的（假设10000 个细胞中用200 个活跃细胞来表示模式），而记录20 个细胞和记录所有的细胞效果相同。实际系统中的误报率是极小的并且也可尽量减少使用的内存。

图2 HTM时间池模型

子抽样应用贯穿于整个HTM 算法，其思想为HTM 区域中的细胞利用稀疏离散表征这一特性，可以理解为任何一个细胞附近可能有成千上百个活跃细胞但树突区域只需连接其中的15～20 个这样的树突。当树突区域连接到其中15 个时，可认为正在产生可以学习到的模式。

每个细胞都参与到多重的离散模式和不同的序列，因此每个细胞拥有不止一个的树突区域。理论上每个细胞为最佳识别的活跃模式分配一个树突区域，然而实际上一个树突区域可以学习多个差异明显的模式连接并且可以保证质量地完成工作。尽管在一定巧合下，不同模式对应的活跃连接会达到树突区域的阈值，这种错误由于表征的稀疏性发生的概率很小。

3 支持向量机算法（SVM）的基本原理

3.1 SVM的基本思想

基于VC维理论和结构风险最小化理论的支持向量机是统计机器学习的核心内容。为了获得最好的推广能力，支持向量机在对给定的数据逼近的精度与逼近函数的复杂性之间寻求折中方法。通过用内积函数定义的非线性变换将输入空间变换到一个高维特征空间，并在高维特征空间中寻找输入变量和输出变量之间的一种非线性关系［9～10］，巧妙地解决了维数问题。

3.2 SVM模型建立

第一步，对数据的预处理细节实现分析部分将会详细介绍。

第二步，基于原始数据数列做一次累加生成，建立GM（1，1）模型的基本形式得到紧邻均值生成序列，构造灰色微分方程，对11 组数据税收样本数据进行学习，求解税收预测值Yi。

第三步，利用默认参数建立基于支持向量机的税收预测函数：

其中，k（x，xi）为核函数，核函数的选取应使其成为特征空间的一个点积，表明存在一个函数φ，使φ（xi）·φ（xj）=k（xi，xj）成立。

第四步，应用5 组测试数据集进行预测验证试验，2013～2017年税收预测误差表如2所示。最后，预测2018～2020 年的税收收入预测值，预测结果如表3所示。

表3 2018～2020年税收预测数据

4 实验分析

4.1 数据来源

根据相关参考文献选择某市税收收入的影响因子，依据指标在《统计年鉴》中收集相关税收数据。采用某市地区生产总值X1（亿元）、户籍总人口X2（万人）、第一产业增加值X3（亿元）、第二产业增加值X4（亿元）、第三产业增加值X5（亿元）、财政总支出X6（亿元）、城镇常住居民人均可支配收入X7（元）、农村人均纯收入X8（元）、财政总收入X9（亿元）为HTM 预测摸型的输入量，输出量为某市预测税收值Y（亿元）。

采用2002～2014 年的某市地区生产总值X1（亿元）、户籍总人口X2（万人）、第一产业增加值X3（亿元）、第二产业增加值X4（亿元）、第三产业增加值X5（亿元）、财政总支出X6（亿元）、城镇常住居民人均可支配收入X7（元）、农村人均纯收入X8（元）、财政总收入X9（亿元）作为HTM 预测摸型的输入训练数据，采用2015～2017 年的税收数据作为输出数据，由此得到神经模型。2002～2018 年某市税收及指标因子数据如表1 所示，2020～2018 年税收收入曲线变化如图3所示。

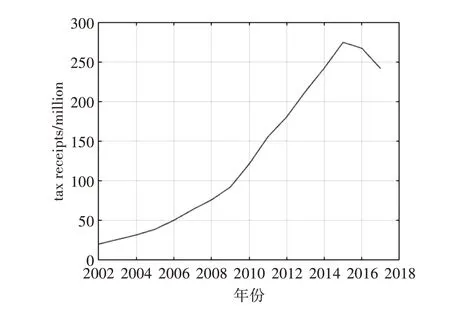
图3 2020～2018年税收收入曲线变化

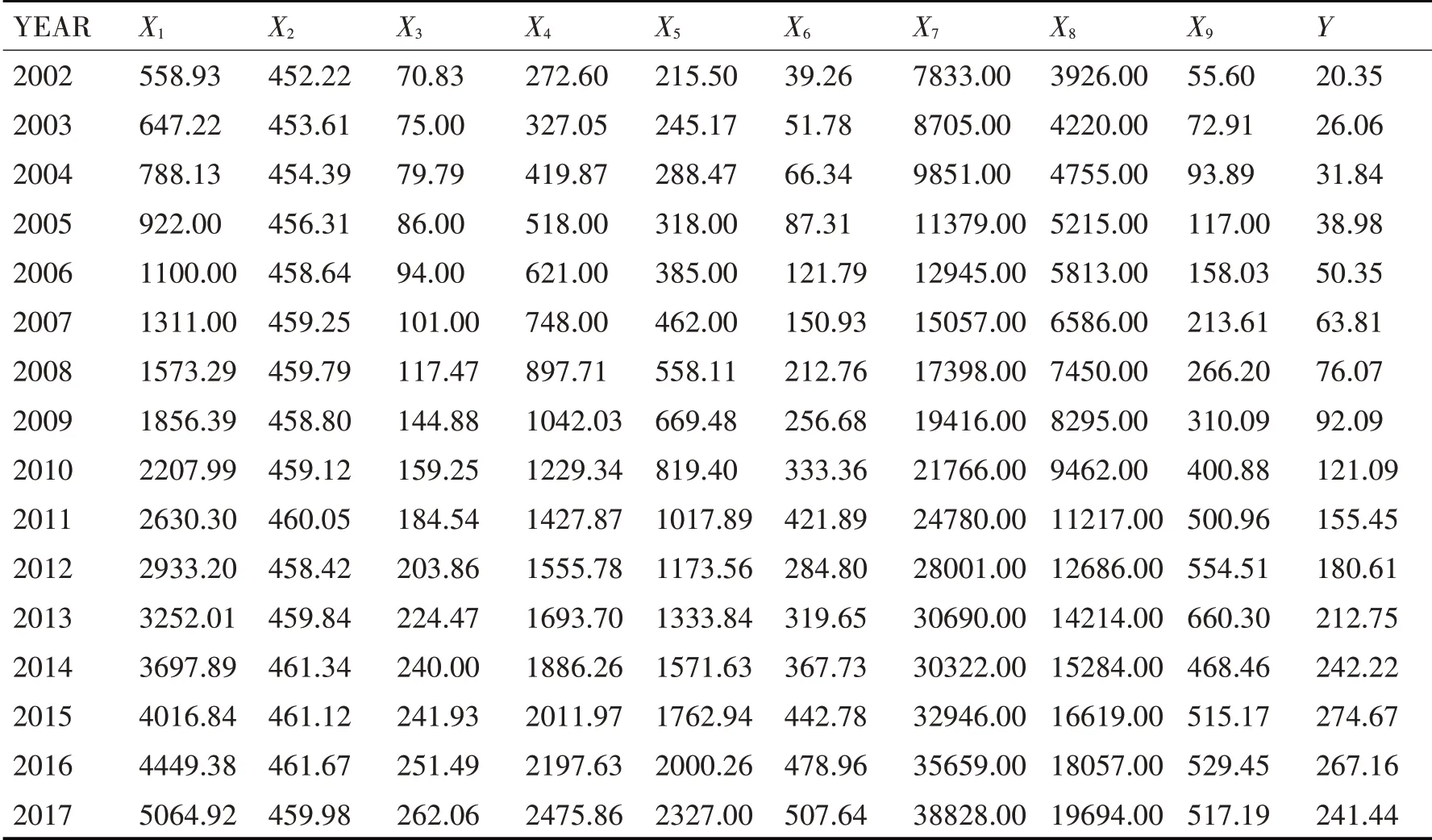
表1 2002-2018年某市税收及指标因子数据

选取影响税收收入的由于实验数据的量纲性差异和数据单位的不统一影响预测模型的的结果以及模型精度，本文在训练模型之前先采用数据归一化预处理［11］，消除预测数据之间的差异，提高预测模型的性能。即把所有数据归一化到［0，1］区间，具体处理过程如式（1）所示。

其中，Mi表示归一化后的税收值，Xi表示税收数据实际值，Xmin和Xmax分别表示实际税收序列中的最小值和最大值。

4.2 结果分析

根据上文两种方法进行实验预测所得以下结果。图4为2013～2017年税收预测值曲线与真实值的对比偏离程度，其中Data1 曲线是2013～2017 年实际税收收入，Data2与Data3分别是支持向量机预测模型和层级时序记忆算法预测模型的税收预测值。为了评价预测方法的有效性，本文选择绝对误差作为评价指标。由表2 可以看出两种税收预测模型分别实现了对2013～2017年共5年的税收样本数据进行测试，误差值如表2 所示。误差曲线变化如图5所示。

图4 2013～2017年税收预测值曲线

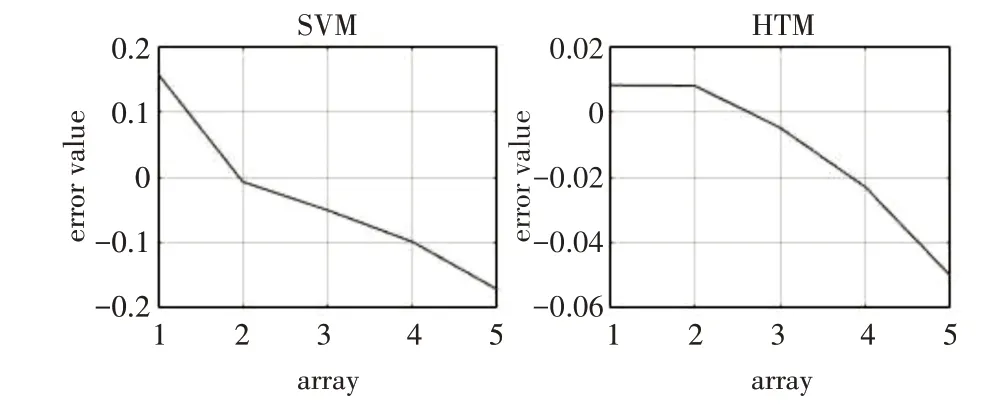
图5 误差曲线变化图

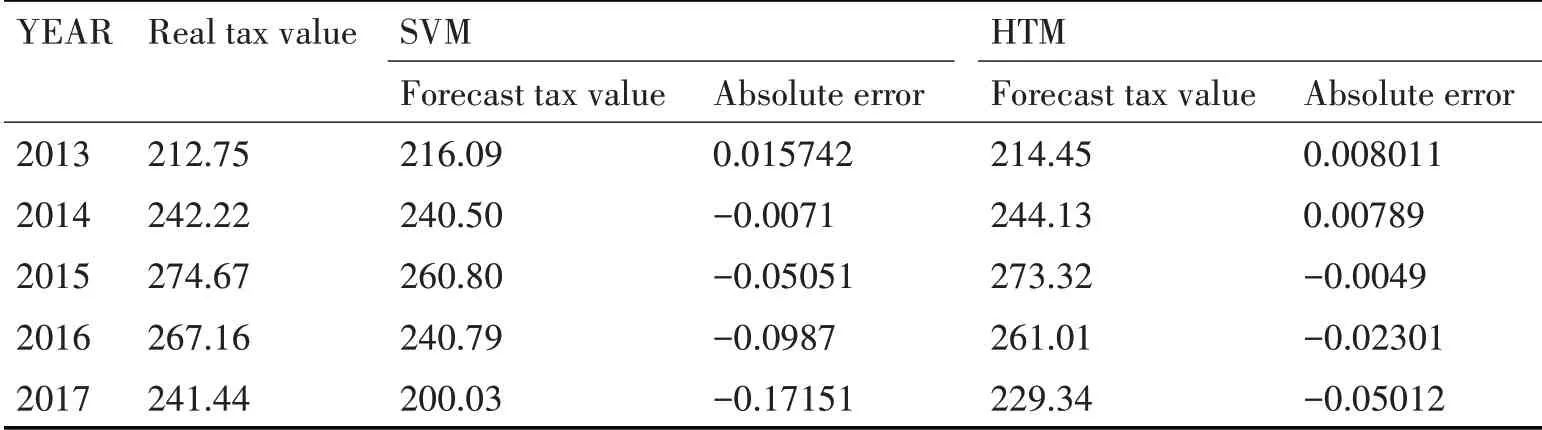
表2 税收预测误差值

基于支持向量机的预测模型的结果稳定，但是预测精度不高，层级时序记忆算法预测结果稳定，而且预测精度提高了。所以本文最终选取层级时序记忆算法预测模型作为最终的预测模型。

根据上述指标评价证实了两种预测方法的有效性，现根据两种模型预测未来三年的税收结果。

5 结语

由于正则化参数和径向基核函数的参数直接影响支持向量机预测模型的优劣，所以预测过程中将预测结果与训练数据的实际结果进行比较，需要不断调整预测模型，预测精度相对不高，实际操作的时间较长。层级时序记忆算法这种新型神经网络，通过感知数据流训练自身，其技能很大程序上由训练它的数据决定。层级能减少训练时间，减少空间使用，提供泛化框架，进而预测结果稳定，而且预测精度提高。最后通过对比试验可以验证层级时序记忆算法预测模型预测性能可行且实用。研究HTM 在模型规模较大预测时，还未能利用多核计算实现训练过程中的并行，模型训练速度尚需加强提高。