基于特征分组和PSO 的特征选择算法*

余肖生 江 川 陈 鹏

（三峡大学计算机与信息学院 宜昌 443002）

1 引言

特征选择，即从一个特征集中选择出一部分重要的特征，是数据处理中的关键步骤之一，其能起到降维，减少数据存储空间的效果［1］。若数据集中存在n维特征，使用特征选择进行搜索存在着2n种结果［2］。每一种结果都会耗费大量的时间和计算成本，对后面数据分析等步骤造成不利的影响，若选择出部分重要特征再进行分析，可以大大降低时间和计算成本。特征选择方法总体可以分为过滤式、封装式和嵌入式方法［3～4］。近年来，针对高维数据的特征选择，有不少研究者使用了演化算法来进行，如遗传算法、蚁群算法和粒子群算法等［5～8］。演化算法每迭代一次，便可以得到一组解，不需要多次进行全局搜索，花费时间和计算量较小。因演化算法是通过迭代实现特征选择，每一次得到的结果建立在上一次的结果上，容易陷入局部最优化。Zhu 等局部搜索方法和遗传算法进行结合，添加了包裹式方法，减少了因搜索需要的大量时间［9～10］。Xue 等提出了基于粒子群优化的特征选择算法PSO，在多个目标下达到最优［11～12］。Tabakhi等使用蚁群算法的无监督特征选择方法，搜索空间使用无向加权图来表示，使搜索空间减小了［13］。这些方法主要从演化算法的角度出发，针对特征选择出来的结果进行一次次的迭代，不断得到更好的特征选择结果，针对演化算法迭代时容易陷入局部最优的特点，加入了其他的方法进行了改进，从而使结果有了一定的进步。由于方法使用较多，使算法的复杂性明显上升，考虑的指标也只有样本分类的精确度，忽略了特征选择稳定性。从而导致每次选出的特征子集出现较大变化，以致影响了结果的鲁棒性。而在基因标记等应用中，特征选择结果的稳定性要求要远远高于精确度的要求［14～15］，所以选择出的特征子集的稳定性也是至关重要的［16］。

为了提升特征选择的稳定性和降低特征子集的冗余度，笔者提出了基于特征分组和PSO的特征选择算法，即以特征间的关联性对原始特征进行了分组，对分组后的特征使用PSO 算法进行选择，在选择过程中，为了避免算法陷入局部最优，对部分粒子的值进行了随机扰动，最后对选取的特征进行集成。以特征间的关联性分组，减小了特征选择的维度，也降低了每组特征的冗余，使PSO 算法进行特征选择时提高了初始化种群质量，最终选择出更稳定的特征子集。

2 相关理论知识

2.1 互信息

互信息是信息论中的一种信息度量方式，用于测量变量间相互依赖的程度。通过互信息，可以从一个变量中了解到另一变量的具体信息量，当互信息的值变大时，说明从一个特征了解另一特征的信息越多。对于两个离散随机变量X 和Y，它们的互信息可以定义为

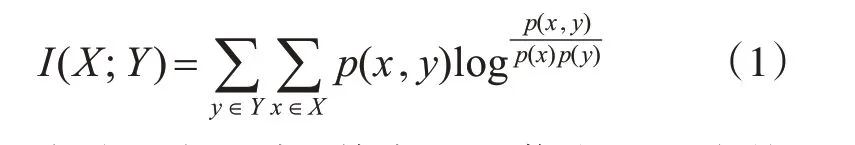
在连续随机变量中，其中的互信息可以变换成：

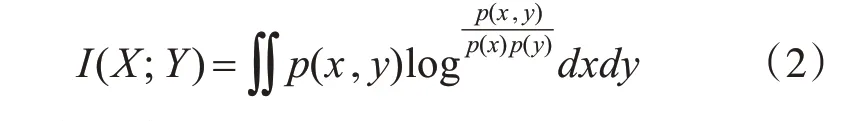
其中，联合概率密度函数表示为p（x，y），x 和y 的边缘概率密度函数表示为p（x）和p（y）。

通过式（1）、（2）可得，若X 和Y 相互独立，则X对Y 不提供任何信息，所得的互信息值为零，当X和Y 关系越密切时，所得的值越大。当X 与Y 表示特征和标签之间的联系时，互信息值越大，则特征和标签的关联性越强；当X 与Y 同时表示特征时，互信息值越大，则特征间的冗余性越强。

2.2 PSO

PSO 算法模仿鸟群，鸟群以合作的方式来寻找食物。其寻找过程是通过一次次的迭代得到目前最优的速度和位置，进而得到整个种群中食物的位置。在PSO模型中，优化问题的解作为解空间的一个粒子，粒子的位置和速度决定着它们下次迭代的方向，根据当前最优的粒子来不断调整自己的状态。在t+1代粒子i的速度根据式（3）进行更新：

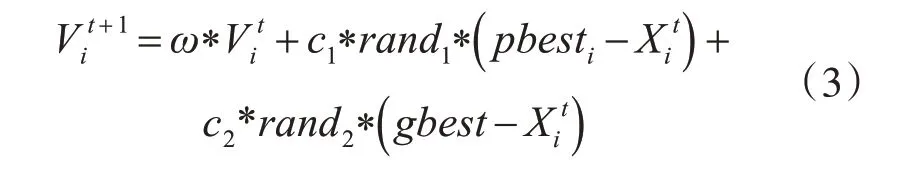
在t+1代粒子i的位置根据式（4）进行更新：

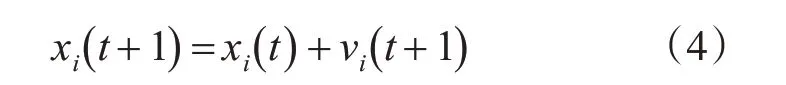
其中，w 表示惯性权重，第t+1代粒子的具体运动情况由第t 代的值来决定，参数c1和c2为粒子的学习因子，rand1和rand2是位于［0，1］的值，实验时由具体的情况进行设定。

2.3 稳定性提升方法

近年来，随着研究的不断深入，研究人员根据不同的问题，提出了一些稳定性提升算法。Zhou使用Bootstrap方法抽样数据得到多个特征子集，随机移除特征子集中的特征，使用Relief 特征选择方法对特征进行排序，通过移除不同特征，使用算法得到排序不变的特征，并筛选出这些不变的特征［17］。Yang 对原始数据特征使用不同规模的采样，生成不同的训练样本，最后集成特征选择的结果，来提高特征选择的稳定性［18］。Aldehim 使用集成的方法，集成不同方法得到的结果，提升特征子集的稳定性［19～20］。这些方法使用了多种特征选择方法，对特征选择出来的结果进行了集成，提高了特征选择的稳定性，但是采用方法过多，导致复杂性上升，每一种方法考虑其自身的优点，却没有考虑方法之间的联系和特征之间的前后关联，也较少考虑精确度和高维小样本问题。

3 基于特征分组和PSO 的特征选择算法

从稳定性角度看，传统算法和演化特征选择算法具有一定的效果。在特征选择中，针对传统方法时间复杂度较高等不足，笔者将特征进行分组，对原始特征进行降维，降低时间复杂度。针对演化算法没有考虑特征间的关联性，导致选出的特征存在部分冗余，在分组时考虑特征间的关联性，使特征子集间的耦合度降低，并对少部分粒子进行随机扰动，避免了算法陷入局部最优，对最后的特征子集进行集成，得到稳定的特征子集，具体流程图如图1所示。

图1 算法流程图

3.1 特征分组

在高维特征选择方面，演化算法所选出的最终特征容易出现不稳定。针对这一不足，笔者将原始的数据特征进行分组，相较于原始的高维特征，分组后的每组特征维度降低。为了选取更有效的特征，分组特征所使用的算法是互信息与随机森林。首先通过随机森林算法对特征的重要性进行排序，能识别出分类结果的排在前面。根据排序的结果，选出最前列的四个特征与其他特征进行互信息计算，得到特征间的互信息值，其余的每个特征与前四个特征中互信息值最大的分为一组，可得到四个特征组。

分组完成后，相较于原始特征集，特征维度降低，特征组间的冗余信息较少。特征组内的关联度较高，在使用PSO 算法做特征选择时，粒子的搜索空间减小，时间的复杂度降低。因每组特征内的关联度高，提升了粒子初始化种群的质量，进而每组特征能选择出更重要的特征。

3.2 PSO进行特征选择

根据第一步得到的特征分组后，笔者使用了粒子群算法对分组后的特征进行了选择。

3.2.1 种群的初始化

速度和位置两个参数决定了粒子运动的具体情况，位置决定了距离最优值的距离，速度迭代时变化的大小。在粒子群算法中。粒子的特征值每一维中只能取1或者0，1预示着该维特征在本轮迭代中被选择，0 则预示在本轮迭代中被舍弃，针对整个粒子的种群，可得到本轮迭代时的一种特征选择结果。在粒子群算法开始时，针对所有的粒子赋初始值。具体的初始区间为［0，1］，为了便于统计和观察，当初始值大于0.5 时，则赋值为1，当初始值小于等于0.5 时，则赋值为0，通过x（i，j）来进行记录，i 代表第i 行的样本，j 代表第j 维特征。可以得到，在初始化过程中，所选出的特征总数占原始特征的50%，满足一般的特征选择要求。具体公式如（5）所示：

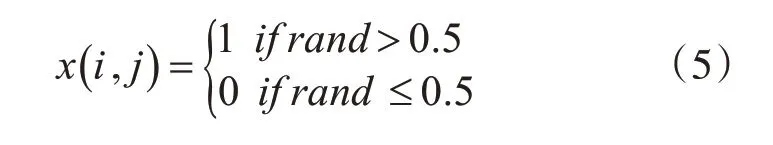
个体粒子初始pbest 为其粒子的本身，初始化gbest随机记录为某一粒子。

3.2.2 迭代的过程及结果

在迭代过程中粒子的速度和位置更新按照式（3）和式（4）进行更新。每次迭代之后得到的结果，从实际情况出发，特征选择不仅仅需要考虑的是特征最后选出的维数，还需要考虑样本分类的精确度，笔者使用这两种目标进行联合判定粒子所选出的优劣程度，所立的适应度函数精确度占比为0.8，特征维数为0.2，具体公式如式（6）所示：

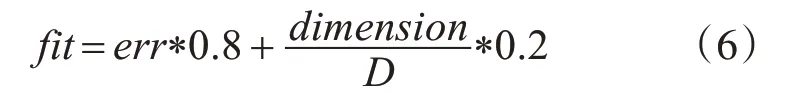
其中，fit 为适应度值，err 为错误率，来源于分类的结果，dimension 为所选的特征数，D 为原始的总特征数。

为了避免因粒子陷入局部而使结果存现偏差，在粒子选择的过程中，笔者对粒子进行了随机扰动，避免粒子陷入局部最优化，具体的过程为，对x（i，j）的值进行更改，更改的总数占整个矩阵的5%，更改的位置为迭代总数的60%。具体的更改公式如式（7）所示：

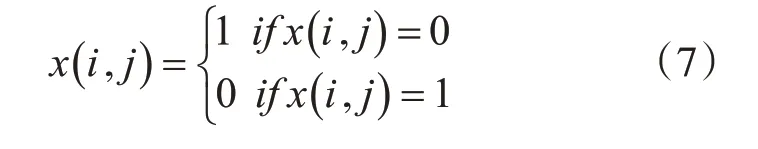
4 实验及结果分析

4.1 实验参数设置

所有的实验均是在内存8.00GB，处理器为Intel 上运行的，运行环境为MatlabR2016。在算法运算过程中，为了更具有代表性，分类器的使用中，选择了KNN（K=5）算法和SVM 算法。粒子群的参数设置中，种群大小N=30，最大迭代次数T=100，惯性权重随迭代次数的增加而更改，最大ω（max）=0.8，最小ω（min）=0.4。学习因子c1=c2=2，粒子的最大速度V（max）=10，最小速度V（min）=-10。表1 为本文所采用的5 个公开数据集。数据集来源于UCI 学习网站和http：//featureselection.asu.edu/datasets.php两个网站。

表1 数据集信息

4.2 常用的稳定性度量方法

稳定性度量指标是对特征选择结果的一种评判。根据现有研究，不同的评价指标往往决定了不同的特征选择稳定性结果。根据特征选择不同的度量方法，具体可以分为权重法、子集法和排序法。其中排序法通过对部分排序列表进行度量，考察排序向量的相似性。子集法通过子集间同一特征的距离度量来评判特征间的相似性［21～22］。每一种方法都可以从一方面或一些方面来度量特征选择的稳定性。

本文使用的稳定性度量方法主要有两种，其一为特征的重复率，在两个特征子集中，存在相同的特征越多，说明稳定性越高，如式（8）所示。

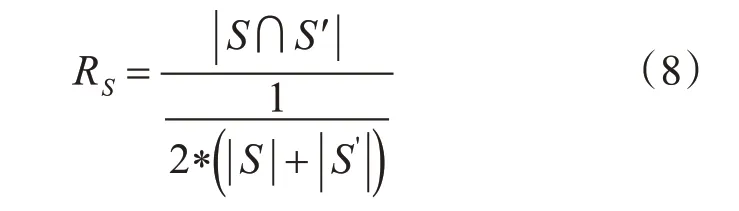
S 和S'为实验中的两个特征子集，S∩S′表示选出两个子集共有的特征。

其二为斯皮尔曼排序相关系数。针对共有的特征进行度量不够深入，因特征间的排列顺序和重要性不一样，排列顺序往往影响着特征的重要性。因此引入度量指标斯皮尔曼排序相关系数，如式（9）所示。

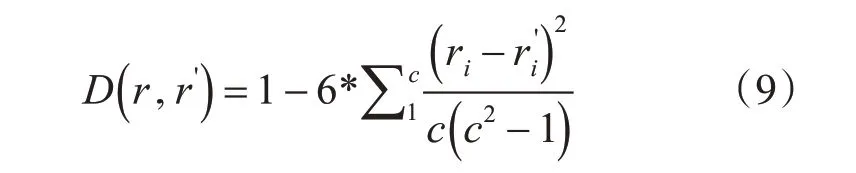
其中，ri和ri'是共有的特征i 在向量r 和r'中的位置，一共有c个共同的项。

4.3 实验稳定性分析

从相关网站上采取了数据集后，笔者利用所提出的方法完成了相关的实验。在高维小样本中，样本的变化导致选出的特征出现变化，本实验随机删除5 个样本和增加5 个原始中存在的样本，分析原始样本和增删样本的特征子集变化情况。为了验证方法的有效性，本方法记作DGBPSO（divide group about BPSO）并和原始的BPSO 方法以及遗传算法GA进行了结果对比。特征子集稳定性评判标准采用式（8）和式（9）。所得到的结果如图2～图5所示，为记作简便，横坐标为每个数据集的第一个字母，如ALLAML记作A。

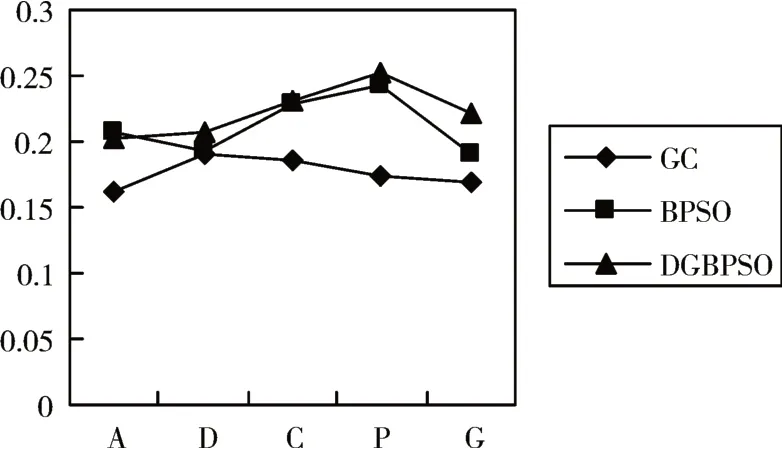
图2 随机减少5个样本对数据集进行运算并使用特征重复率评判准则得到的稳定性结果

图5 增加5个样本对数据集进行运算使用斯皮尔曼系数得到的稳定性结果

对每个数据集随机减少5 个样本，根据图2 可得，在DLBCL、CLL_SUB_111、Prosate_GE 和GLI_85四个数据集上，DGBPSO算法都比BPSO和GC算法特征重复率高，在数据集ALLAML 上，DGBPSO算法比不上BPSO 算法。在DLBCL 数据集上，特征重复率相较于BPSO 提高了7.4%；CLL_SUB_111 提高了0.48%；Prosate_GE 提高了3.8%；GLI_85 提高了16.2%。相较于BPSO 和GC 算法，DGBPSO 算法优点在于根据特征分组，缩小了特征维度，粒子所寻找到的特征则有更大的相似性，进而稳定性更高，算法得到了改进。

在上述减少5 个样本得到的特征子集上，笔者也选取了斯皮尔曼系数进行了评判，根据图3 可得，在ALLAML、CLL_SUB_111、Prostate_GE、GLI_85 数据集上，DGBPSO 方法比BPSO 和GC 方法要好，在DLBCL 数据集上比GC 方法好，没有BPSO 方法优秀。相较于传统的BPSO 方法，在ALLAML 数据集上，DGBPSO 提高了8.7%，CLL_SUB_111 提高了3.9%，Prosate_GE 提高了13.1%，GLI_85 提高了0.9%，可以看出在ALLAML 和Prosate_GE 数据集上，提升得比较明显。

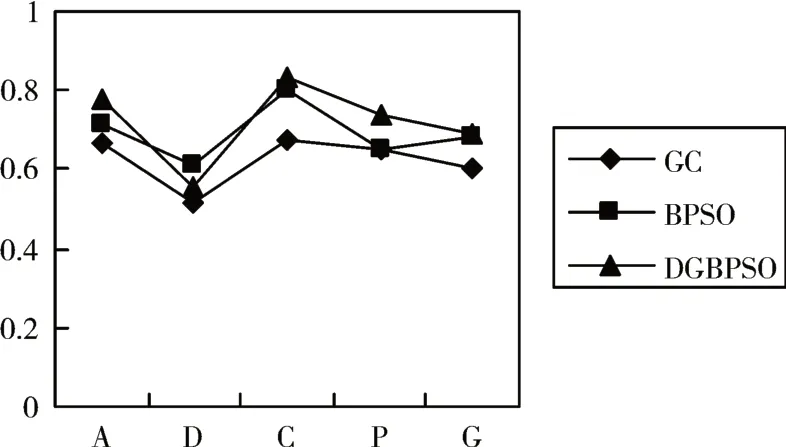
图3 随机减少5个样本对数据集进行运算使用斯皮尔曼系数得到的稳定性结果

在增加5 个样本的条件下，根据图4 可得，在ALLAML、DLBCL、Prosate_GE、GLI_85 数据集上，相较于GC和BPSO算法，本文的DGBPSO算法有较大提升，在CLL_SUB_111 数据集上，表现略差于BPSO 算法。其中数据集ALLAML提升了1%；数据集DLBCL 提升了2.3%，数据集Prosate_GE 提升了7.1%，数据集GLI_85 提升了17.2%。根据现有的研究理论，增加样本可以提高特征选择的稳定性，结合图3和图4可以看出，在相差10个样本中，DGBPSO 算法在增加样本的情况下，表现的比减少样本的实验好。

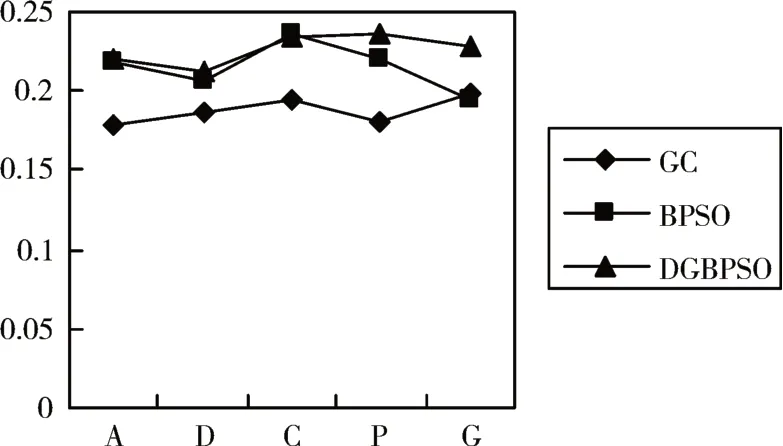
图4 增加5个样本对数据集进行运算使用特征重复率准则得到的稳定性结果

在增加5个样本的基础上，根据图5可得，在数据集ALLAML、CLL_SUB_111、Prosate_GE 上，DGBPSO算法得出的结果要优于GC和BPSO算法，数据集CLI_85 和DLBCL 上，DGBPSO 算法要略差于BPSO 算法。相较于传统的BPSO 算法，在数据集ALLAML 上，提升了5.9%；在数据集CLL_SUB_111上，提升了6.4%，在数据集Prosate_GE 上提升了7.1%。

针对选择出来的特征，在稳定性方面有了一定的提升，如果选出的特征，却对分类的准确率没有提高的话，实际应用方面则受到很大的限制。为了验证本方法存在的有效性，笔者对上述几种方法所得到的准确率进行了总结和概括。对于演化算法容易陷入局部最优的特点，本文所提出的对数据进行扰动存在的可行性，只对粒子群算法进行分组，不进行数据扰动的算法记作IBPSO 算法，可以所得到的结果如图6和图7。

图6 使用KNN分类器对数据集进行测试所得到的准确率

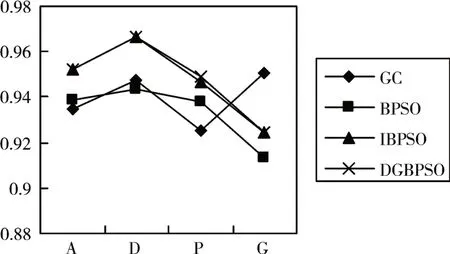
图7 使用SVM分类器对数据集进行测试所得到的准确率

根据图6 的数据可得，DGBPSO 算法在数据集ALLAML、DLBCL、CLL_SUB_111 表现比GC 和BPSO 算法好。相较于BPSO 算法，数据集ALLAML 提升了5.1%，数据集DLBCL 提升了1.1%，数据集CLL_SUB_111 提升了6.3%。五个数据集中有三个数据集有较明显提升，取得了比较好的效果。对于没有加入数据扰动部分的IBPSO 算法，可以看出，在数据集CLL_SUB_111 和Prosate_GE 中陷入了局部最优化，加入数据扰动，有了一定的提升，数据集Prosate_GE 虽没有BPSO 效果好，但比没有加入时提升了1.0%。

因SVM 分类器常用于二分类问题，使用SVM分类器对四个数据集进行了分析，根据图7 可得，在数据集ALLAML、DLBCL、Prosate_GE 中有了一定的提升。相较于BPSO 算法，DGBPSO 算法在数据集ALLAML 提升了2.5%，数据集DLBCL 提升了2.4%，Prosate_GE 数据集提升了1.2%，而在GLI_85数据集中，结合图6，可以看到GC 算法所得到的准确率更高，说明GLI_85 数据集更适合于GC 算法。对于没有加入扰动的IBPSO 算法，在数据集Prosate_GE 中有了一定的提升，提升效果为0.3%，其余数据集均没有变化。说明加入扰动部分能够一定程度地避免算法陷入局部最优过程中。

5 结语

为了提高高维小样本数据特征选择的稳定性，笔者提出了基于特征分组和PSO的特征选择模型，即先通过互信息对特征进行分组，根据特征关联性强弱分为不同组，待分组后，利用PSO 算法对特征进行了选择。为了避免粒子陷入局部最优，在选择过程中对少部分粒子进行随机扰动。最后利用两种稳定性度量指标评判所选择特征的稳定性。与现有方法相比，本算法提高了特征选择的稳定性，在分类精度方面，其中部分数据集也取得更好的结果，同时满足了特征选择的稳定性和分类精度，拓宽了算法的应用范围。