基于正弦振动的起落架舱耐久性分析

张 壮，郭 峰

（中航西飞民用飞机有限责任公司，陕西 西安 710089）

飞机在飞行过程中要承受复杂的振动激励，典型的飞机振源包含了推进系统产生的振动与噪声激励、非平稳气动力、螺旋桨产生的不平衡力等。这些振源可分为周期振动、随机振动以及瞬态振动。这些振动可能会引起飞机结构的局部应力过大，甚至疲劳破坏[1-2]。因此在飞机设计中一般都要求对结构进行强度校核分析以及振动耐久性试验。

由于振动耐久性试验周期长，花费高，故在试验之前都要进行仿真分析，对结构的疲劳损伤进行初步的判断和评估。耐久性试验主要分为随机振动试验和正弦振动试验。目前，关于随机振动的耐久性理论计算和分析较为全面[3-6]，关于正弦振动的耐久性计算较少，方红荣、薛立鹏等仅针对航天结构的最大应力处进行振动耐久性校核，未考虑其他较大位置的损伤累积影响和在三个方向振动的损伤累积[7-8]。

本文以某涡桨飞机起落架舱为研究对象，基于Miner 线性累积损伤理论，采用简化的损伤累积计算公式进行结构的所有节点在三个方向振动的耐久性计算。

1 正弦振动试验及疲劳寿命理论

1.1 正弦振动试验

为了模拟振动环境激励，找到产品结构的共振频率，对产品结构进行耐扫频以及耐扫频后的共振检查，通常进行振动试验。此涡桨飞机主要振源在螺旋桨以及发动机处，以周期振动为主。本文主要以正弦对数扫频为振动激励进行分析。

正弦振动试验分为定频试验和扫频试验，扫频试验又分为线性扫描和对数扫描[9]。扫频试验中频率按照一定规律发生变化，而振动量级是频率的函数。线性扫描频率的变化是线性的，用于细找共振频率；对数扫描频率按对数变化，即相同时间扫过的倍频程是相同的。

1.2 疲劳寿命理论

实际疲劳寿命的估算可以用疲劳累积损伤定律，最简单的是Miner 线性累积损伤理论[10]，它认为部分疲劳损伤可以线性叠加。通过正弦扫频振动分析得到结构应力随频率变化的频域描述，基于结构各节点的应力曲线，结合Miner 线性累积损伤理论，可以计算其疲劳寿命。在正弦扫频振动分析中，作出如下假设[11]：

(1)共振峰值应力是造成损伤的主要原因；

(2)共振峰扫频时间按照半功率时间计算。

基于以上假设，可将节点应力随频率变化曲线离散为若干个共振峰，将每一个共振峰的应力值和共振峰时间作为一级应力幅值循环。

Miner 线性累积损伤理论将疲劳损伤DL 定义为使用应力下的循环次数n 与该应力下材料疲劳寿命N 的比：

在多级不同应力幅值作用下，构件未发生疲劳破坏的条件：

式中： —第i 个节点在l 方向的损伤累积。

nj—第j 级应力水平下的循环次数，对应于正弦振动的第j 个共振频率下的振动次数。

Nj—第j 级应力水平下的疲劳寿命，源自于对应材料的S-N 曲线。

正弦振动中，上扫或下扫时间t、频率f、扫频速率Rs和半功率时间Th关系为：

一次上扫或下扫时间：

半功率时间：

一小时正弦扫频次数：

式中：f1、f2—分别为扫频起始频率和终止频率；

fN—共振频率。

在正弦振动试验中，通常将一个试件分别进行X 向、Y 向以及Z 向一个小时的振动，因此需要累加三个方向的损伤。

1.3 应用

文献[7-8]中基于正弦振动疲劳损伤累积，根据应力在频域的描述，利用振动时间和频率的关系将损伤累积的时间积分转化为频率积分，进而对频率进行离散化，得到最终的累积损伤。本文根据文献[11] 中电子设备结构常用的过谐振点的正弦扫频疲劳循环计算方法，认为结构在扫描期间累积的损伤，大多数会发生在峰值谐振点附近，并且采用半功率点这个方便的基准，直接对文献[7-8]中的损伤累积公式在时域和频域上进行离散，得到简化后的正弦疲劳损伤累积计算式。

2 起落架舱概述

2.1 模型概述

本文以某飞机起落架舱为研究对象，起落架舱结构用于起落架舱区域机身开口的气密密封，并保持起落架舱区域机身结构的完整性。起落架舱结构包括框、龙骨梁以及气密夹板等，框以及龙骨梁上部为7050-T7451 材料，龙骨梁下部以及气密夹板等为2024-T3 材料。

2.2 有限元模型

框、气密夹板、龙骨梁简化为壳单元，角钢、Z 型材简化为梁单元。按照与机身相连以及由于简化建模而打断的结构均需施加振动载荷的原则，将30 框、33 框、31 框-32 框与地板骨架连接点使用刚体元（RBE2）连至约束点，然后约束点固支，刚体元释放三个转动自由度，在约束点上分别施加X 向、Y 向、Z 向正弦振动载荷，振动频率范围为5~500 Hz，载荷按照试验曲线进行加载，见图1。根据ESDU 73011A，阻尼比采用5Hz∶0.016，145 Hz∶0.016，500 Hz∶0.005。建立的起落架舱有限元模型见图2。

图1 输入载荷

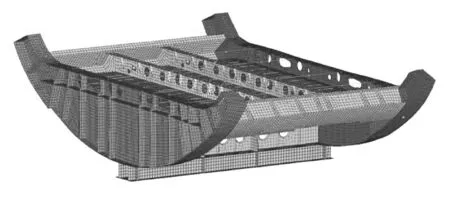
图2 起落架舱有限元模型

3 起落架舱分析

3.1 振动分析

对起落架舱约束点以强迫位移的方式施加正弦振动激励，进行频响分析，并按照共振频率输出结构各节点的Von Mises 应力，得到不同材料各节点的应力云图以及应力响应谱。在X 向、Y 向、Z 向三个方向正弦振动载荷下，各材料最大应力见表1。其中7050-T7451 材料和2024-T3 材料在Y 向振动下各节点应力云图和最大应力响应谱见图3。由表1 和图3 可见，起落架舱在Y 向载荷下，振动应力较大，频率均为282.0 Hz，主要位于龙骨梁与框的连接处。

表1 各材料最大应力

图3 各节点应力分布及其最大应力响应谱

3.2 振动耐久性分析

根据Miner 线性累积损伤理论，当DL 值小于1 时，可认为构件不会发生疲劳破坏。7050-T7451铝合金选取MMPDS（KT=3.0，应力比等于-1）的S-N 曲线；2024-T3 铝合金选取2024-T3 铝合金（KT=4.0，平均应力为0.0）的S-N 曲线。振动试验频率范围为5~500 Hz，速率为1.0 oct/min。

为了保证构件能够在振动台实现X 向、Y 向及Z 向三个方向各一个小时的振动需求，需要将各节点在三个方向的疲劳损伤DL 累加，基于Python 编程，得到各节点计算结果，汇总得到的耐久性预测见表2。计算表明，起落架舱在Y 向振动较为严重，7050材料最大累积损伤值为0.380，仅有2 个节点的累积损伤值超过0.200；2024 材料最大累积损伤值为0.223，仅有2 个节点的累积损伤值超过0.200。7050 材料和2024 材料在三个方向振动载荷下疲劳累积损伤值分别为0.382、0.285，预测该结构可承受三个方向各一小时的正弦振动。

表2 节点振动耐久性预测

4 结论

本文以某飞机起落架舱为研究对象，基于Miner 线性累积损伤理论，开展了正弦振动耐久性分析，建立了起落架舱动力学模型，按照试验载荷进行加载，得到结构应力随频率的响应。基于Miner 线性累积损伤理论编写Python 程序，对结构所有节点在三个方向的振动进行耐久性分析，预测该结构可以承受三个方向各一小时的试验振动激励。本方法基于Miner 损伤理论，对应力在频域上的分布直接离散，计算方便，可为类似工程的振动耐久性计算提供参考。