一种双边LCC补偿无线电能传输变换器谐振网络设计方法
2022-06-15苏建徽徐海波
刘 硕,苏建徽,张 健,徐海波
(1. 合肥工业大学 光伏系统教育部工程研究中心,安徽 合肥 230009;2. 东莞南方半导体科技有限公司,广东 东莞 523000)
0 引言
基于松耦合变压器LCT(Loosely Coupled Transformer)的无线电能传输WPT(Wireless Power Trans‐fer)技术适用于电动汽车、轨道交通等大功率场合[1-2]。其中LCT 因耦合度低,需要与补偿元件构成谐振网络,以补偿其无功功率,加强空间磁场[3]。常见的补偿方式有串联-串联SS(Series-Series)等[4]。
文献[5]提出的双边LCC补偿方式,具有谐振频率不受负载及LCT 互感影响、传输功率正比于互感等优点。该文献使用基波法FHA(Fundamental Har‐monic Analysis)分析了双边LCC补偿WPT变换器的基本特性;又考虑到谐波,提出了一种实现逆变电路开关器件零电压开通ZVS(Zero Voltage Switching)的参数设计方法,并为带有磁芯的平面结构LCT[6]配置了补偿元件参数。
相比SS 补偿方式,双边LCC 补偿方式谐振网络复杂,其参数配置具有更多自由度[7]。因此有必要合理设计其谐振网络。相关文献一般将LCT参数作为已知量,如文献[7]基于器件电压与电流应力、谐振网络对3次与5次谐波阻抗、LCT 铜损与铁损等方面的考虑,优化配置了谐振网络中两侧串联电感的比值。文献[3]针对以绝缘栅双极型晶体管IGBT(Insulated Gate Bipolar Transistor)作为开关器件的LCC 补偿WPT 变换器能量发射端,提出了一种实现开关器件零电流关断ZCS(Zero Current Switching)的谐振网络参数设计方法;而文献[8]针对以快恢复二极管作为整流元件的LCC 补偿WPT 变换器能量接收端,提出了一种以临界连续导通模式消除二极管反向恢复损耗的谐振网络参数设计方法。近几年碳化硅(SiC)器件迅速普及。SiC 绝缘栅场效应晶体管(MOS)与IGBT 相比不存在拖尾电流,与SiMOS 相比耐压高,开关损耗低;SiC 二极管与Si 快恢复二极管相比几乎无反向恢复损耗[9]。故采用SiCMOS 与SiC二极管后,不宜沿用文献[3]、[8]的设计思路,因开关损耗与反向恢复损耗不再占较大比例,开关器件内阻与整流二极管死区损耗的影响更加明显,故在谐振网络参数设计上,希望其有较强的谐波抑制能力。目前,相关文献未统筹设计谐振网络中元件电参数,故需要反复交替LCT 设计与补偿元件配置这2个步骤,才可达到满意的设计结果。
虽然空心LCT 参数估算与设计已有广泛研究[10-11],但为了增加耦合度,降低对外界的干扰,用于大功率场合的LCT 带有磁芯,故其设计一般使用建模与运算费时的有限元仿真软件[12],而相关文献没有提供有限元建模前对LCT 尺寸的理论估算,故仿真存在一定的盲目性。目前对LCT的研究热点在于磁集成技术和如何提高耦合度与抗横向偏移能力[1,6]。由于结构简单、节省导线、抗横向偏移能力强,圆形平面螺旋线圈LCT 在工程上较常应用[6],其磁芯有片状、辐射状2 种结构。文献[6]研究表明,对于片状磁芯,磁芯面积大则LCT耦合度高,但磁芯面积超过线圈面积后,耦合度增速明显减缓;对于辐射状磁芯,磁芯密集则耦合度高,但随着密集度增加,耦合度增速明显变缓,并接近片状磁芯效果。对于双边LCC 补偿WPT 变换器,与LCT 尺寸密切相关的参数(即互感)反映了其功率传输能力[5],而目前只有背靠无穷大面积、任意厚度磁材料的一对平行线圈,才能以解析法精确计算得到互感[13-15]。
本文提出了一种双边LCC 补偿WPT 变换器谐振网络电参数设计方案:以抑制谐波电流、缩小磁元件尺寸为目标,依据额定(满载)传输功率等约束条件,确定LCT 互感等电参数。并依据最大传输距离与最大横向偏移等约束条件,提出了相应的带磁芯圆形平面螺旋线圈LCT 设计方案:在有限元仿真之前,从理论上估算LCT尺寸,从而节约仿真时间。最后,通过样机实验验证了本文设计方案的正确性。
1 谐振网络电参数设计
双边LCC补偿WPT变换器拓扑如图1所示。图中:U1为变换器输入电压;I1为输入电流;U2为输出电压;I2为输出电流;RL为变换器的负载电阻;K1—K4构成全桥逆变电路;谐振电感Lf1、Lf2和谐振电容Cf1、Cf2、C1、C2以及LCT构成谐振网络;L1、L2和M分别为LCT 的初级自感、次级自感和互感;D1—D4构成整流电路;C0为输出滤波电容;i1(t)、i2(t)分别为逆变电路输出电流与整流电路输入电流;逆变电路输出电压u1(t)与整流电路输入电压u2(t)分别为幅值是U1与U2的方波。
逆变电路开关角频率等于谐振角频率ω0,且满足[5]:
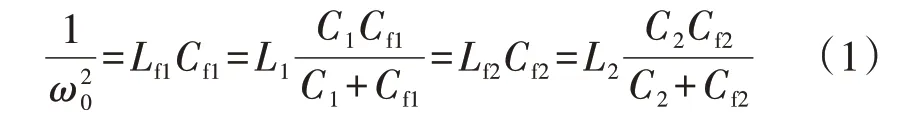
变换器传输功率P为[5]:
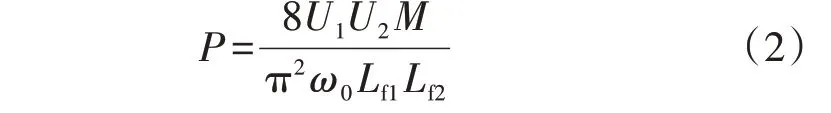
式(2)说明,M/(Lf1Lf2)表征变换器的功率传输能力,在其保持固定的约束下同时减小Lf1、Lf2与M固然能减少磁元件的体积与重量,但这样将降低谐振网络对谐波的阻抗,不利于抑制谐波、降低损耗。
在工程应用中,LCT 初级与次级线圈相对位置变动,导致M不稳定,而式(2)说明图1 中WPT 变换器传输功率正比于M。为了调节与稳定传输功率,一般该WPT 变换器附有前级Buck 变换器或后级Boost 变换器。对于本文即将讨论的后级附加Boost变换器方案(WPT变换器的负载是Boost变换器),其控制策略是,调节Boost 变换器开关管占空比,以稳定Boost 变换器输出电压或电流:当M较低时,调低占空比,使U2上升;当M增加时,调高占空比,使U2下降。
为了在ω0、额定传输功率Pm、最大传输距离、最大横向偏移等已知约束条件下,设计出合理的谐振网络电参数与LCT 尺寸,提出如下4 个步骤的设计方案。
1)步骤1:设计Lf1、Lf2与Cf1、Cf2。
i1(t)与i2(t)中的谐波不参与能量的传递,但会增加逆变电路与整流电路的负担与损耗[7],故谐振元件Lf1、Cf1与Lf2、Cf2应能有效抑制i1(t)与i2(t)中的谐波,但磁件的体积不宜过大。
考虑满载(功率恒为Pm)工况,当M取最小值Mmin时,由式(2)可知,I2处于最小值I2_min,为了在U1固定时维持功率稳定,后级Boost变换器将U2调到最大值U2_max,而I1不变。此时,i2(t)中的总谐波幅值最大,为I2hm_max,i1(t)中的总谐波幅值I1hm与I2hm_max分别为[5]:
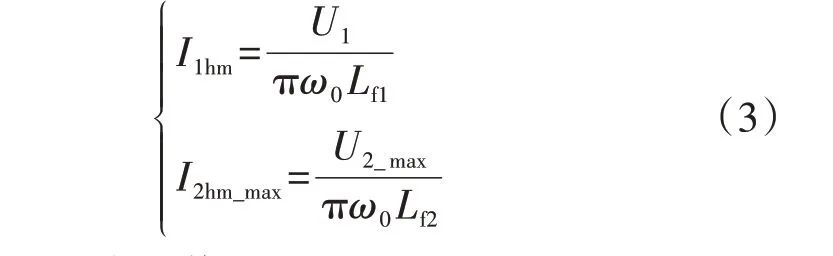
u1(t)的基波幅值U11stm为4U1/π;而此时u2(t)的基波幅值U21stm最大,为U21stm_max=4U2_max/π,因功率由基波传输,故此时i2(t)中基波幅值最小,为I21stm_min,i1(t)中的基波幅值I11stm与I21stm_min分别为:
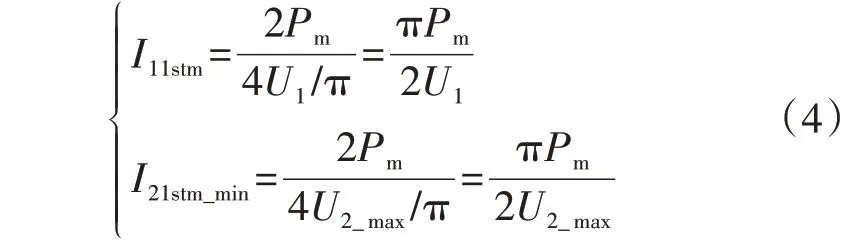
可见在功率固定时,Mmin状态下i2(t)中的基波含量最低而谐波含量最高。现将I1hm限制为λ1I11stm(λ1<1),将I2hm_max限制为λ2I21stm_min(λ2<1),则:
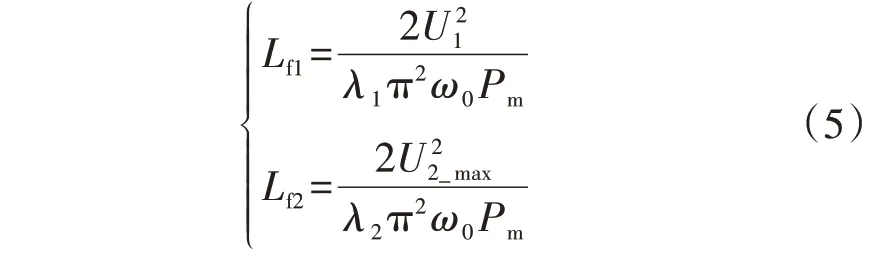
根据式(5)即可得到Lf1和Lf2。其中,系数λ1、λ2的取值反映了在压缩磁元件体积与抑制谐波之间寻求的平衡。分别将λ1、λ2作为参变量,i1(t)和i2(t)的波形分析见附录A,由此可知λ1、λ2分别取0.3、0.2附近较为合适。由式(1)和式(5),可算出Cf1与Cf2。
2)步骤2:设计LCT。
M随LCT 的传输距离h与横向偏移d的增加而减小[6],因此最大传输距离hmax与最大允许横向偏移dmax状态对应着最小互感Mmin。对于双边LCC 补偿方式,P正比于M(见式(2)),故该状态下,应使得在后级Boost变换器占空比为0、U2=U2_max时,传输接近额定功率Pm。
根据式(2)、(5),得到Mmin设计公式为:
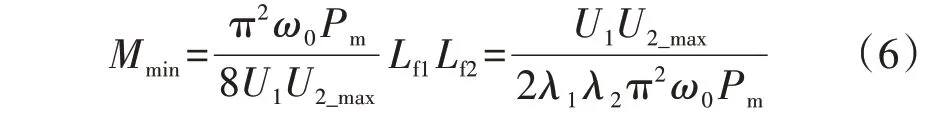
文献[5]中的式(14)、(15)说明,LCT 初级与次级线圈电流表达式不显含M和P;初级线圈电流幅值等于u1(t)的基波幅值除以Lf1对基波的感抗;次级线圈电流幅值等于u2(t)的基波幅值除以Lf2对基波的感抗。结合本文式(5),LCT 初级、次级线圈中电流有效值(ILCT_P、ILCT_S)分别为:
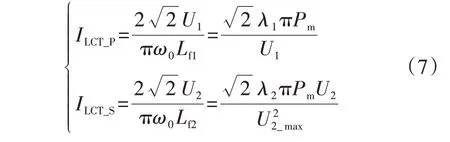
式中:当U2=U2_max时ILCT_S取最大值ILCT_S_max。将LCT初级、次级线圈电流密度都设计为J,则可依据式(7)确定导线导体部分截面积,并选定相应的丝包线,测量其线径(带绝缘层的导线直径)分别为ϕ1和ϕ2。一般LCT 的线圈为单层密绕(螺距为丝包线线径),在多数场合,希望LCT两线圈具有相同的半径,此时LCT的两线圈匝数之比N1∶N2设计为初级、次级线圈线径之比的倒数,即:
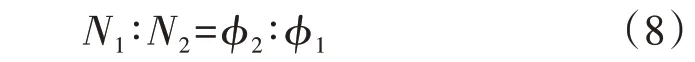
在两线圈半径不同的场合(设初级、次级线圈的内半径之比r01∶r02与外半径之比r1∶r2都等于α),同理依据几何关系得N1∶N2=α·(ϕ2∶ϕ1)。
依据Mmin、N1∶N2、ϕ1和ϕ2,利用有限元仿真软件反复优化,通常做法是,由经验估计LCT 尺寸并建模,运行并记录仿真结果中的互感值,与目标互感值Mmin相比较,再由经验修正模型参数,增大或缩小模型尺寸,重新仿真,如此交替仿真与修正参数过程,直到仿真结果接近Mmin,这样就设计出了LCT尺寸。
3)步骤3:确定C1和C2。
式(1)所示谐振条件包含LCT自感,而其有限元仿真结果与实物往往存在误差。故按上一设计步骤结果制作LCT,并测量hmax与dmax对应的最小自感L1_min与L2_min;又测量最小传输距离hmin与最小横向偏移dmin对应的最大自感L1_max与L2_max(对于平面结构LCT,自感随线圈相对位置变化不敏感[6])。
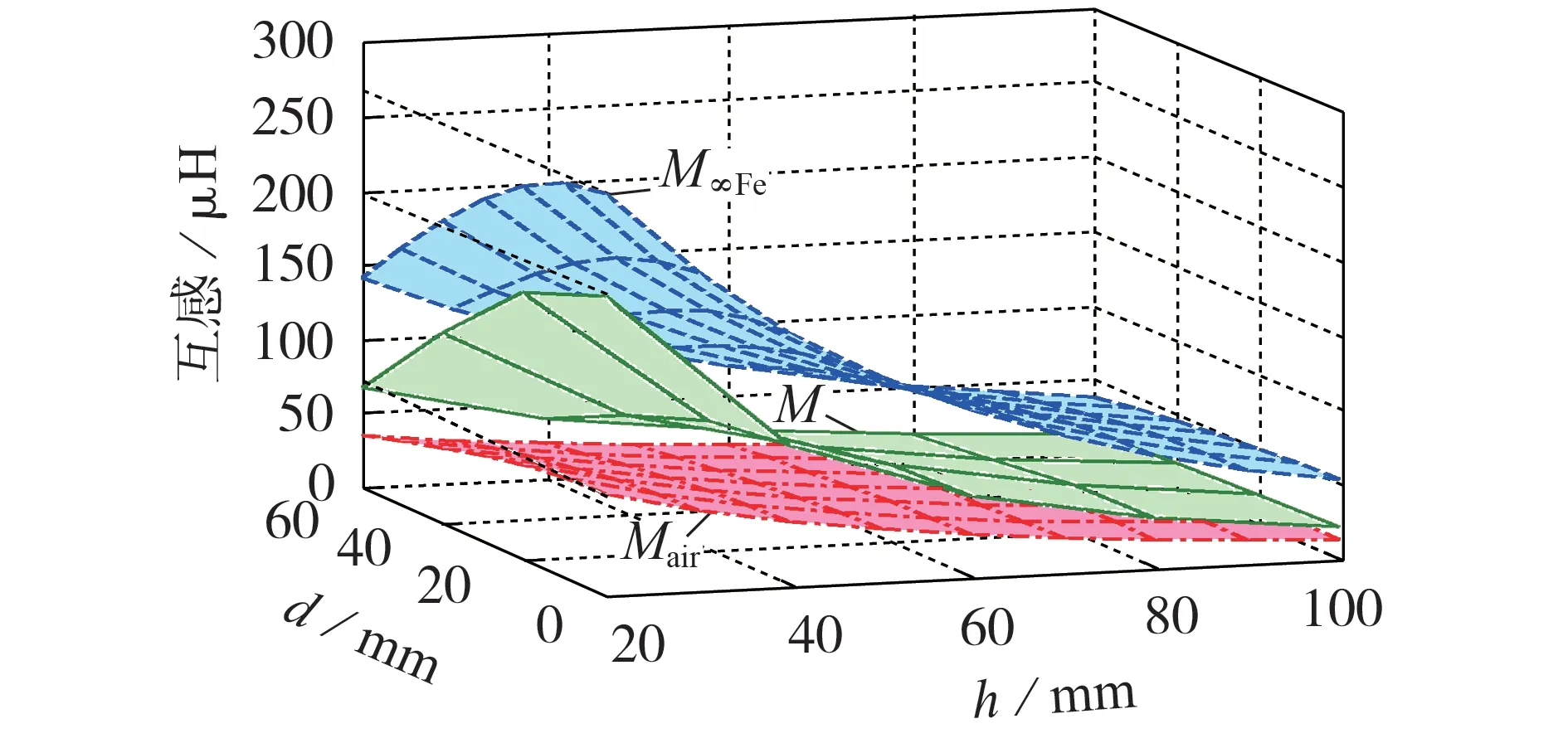
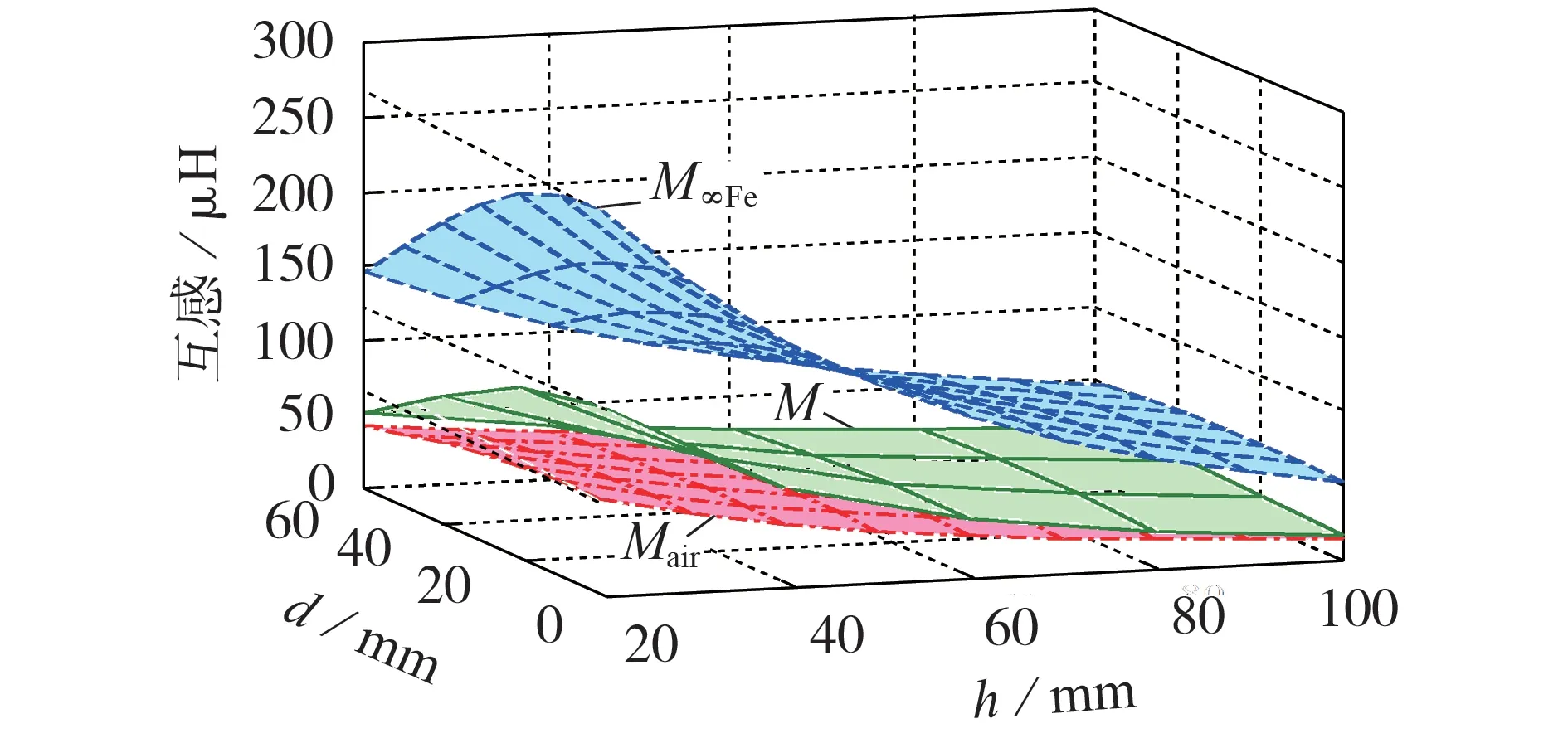
文献[16]的表1 说明,当谐振网络其他元件参数保持不变、LCT 自感偏大导致失谐时,若U1>U2则i1(t)超前u1(t),若U1 对于变换器的逆变电路中使用的SiCMOS,开通损耗大于关断损耗[5],故希望实现ZVS。大多数大功率的工程实例中,U1取自维也纳整流器,超过700 V,而负载是动力电池组,U2一般低于500 V,故将L1_max与L2_max分别作为L1与L2代入式(1)配置C1与C2最合理;反之,在U1 4)步骤4:确定Cf1、Cf2、C1与C2的电压应力。 由于谐波电压大部分降落在电感元件上,故C1和C2的电压应力(UC1m、UC2m)可近似为其基波电流幅值与其对基波容抗的乘积,即: 式(9)不显含M、P,其中ILCT_P与ILCT_S由式(7)确定。 Cf1和Cf2的电压应力也可近似为其基波电压幅值,由于u1(t)与u2(t)的基波相位差接近π/2[5],根据图1,使它们分别作用于谐振网络,利用叠加定理与勾股定理,Cf1与Cf2的电压应力(UCf1m、UCf2m)分别为: 再结合式(1),式(10)可化简为: 在电压应力估算中,M取为Mmax,U11stm和U21stm分别取为4U1/π和4U2_max/π。 综上所述,基于在抑制总谐波幅值与压缩磁元件体积之间寻求平衡的考虑,且保证互感最小时可传输接近额定功率,可设计出图1 拓扑谐振网络(包括LCT)的电参数。 LCT 互感反映了双边LCC 补偿WPT 变换器的功率传输能力。第1节的设计步骤2中,最大传输距离与最大横向偏移状态对应的互感Mmin取值与LCT的尺寸正相关,借助有限元仿真软件反复优化,可在Mmin、N1∶N2、ϕ1和ϕ2约束下设计出LCT,但有限元软件运行费时,通常的设计方法中,有限元仿真次数依赖运气与设计者的工程经验丰富程度。若有限元建模之前,从理论上估算出LCT尺寸范围,则可减少有限元仿真与模型修正次数,节约仿真时间。本节通过对比在不同传输距离与横向偏移状态,背靠大面积片状磁芯的圆形平面螺旋线圈互感磁像法[13]计算结果,及同样的线圈,但磁芯面积与线圈相仿的实际情形的互感有限元计算结果,提出了一种基于半解析解预估-有限元修正的带磁芯圆形平面螺旋线圈LCT设计方法。 对于空心LCT,其互感具有解析解[10-11,13]。若一对平行线圈c1与c2相距h,都背靠面积远大于线圈本身、厚度足以屏蔽LCT 外侧磁场的高磁导率片状铁氧体材料,则根据磁像法[13],线圈电流的镜像分布如图2所示。 图2 一对背靠大面积磁材料的线圈电流镜像分布Fig.2 Mirror current distribution of a couple of coils cling to large area of magnetic material 为了具有足够的机械强度,高磁导率的片状铁氧体磁芯厚度往往足以对LCT 电参数影响较小[17]。图2 中,由于两线圈都紧贴铁氧体,因此电流I1对铁氧体1 的镜像紧贴I1,与c2相距h。I1、对铁氧体2 的镜像、也均与c2相距h。由于铁氧体的相对磁导率μr≫1,根据文献[13]中式(4.111)(即=(μr-1)I1(/μr+1)),、的值都等于I1。I1其他镜像(图2 中未标出)与c2的距离呈h的3、5、7、…倍增长。线圈c1与c2的互感反映了I1及其全部镜像产生的磁场在c2中的通量,文献[11]的计算结果表明,与相比,I1其他离c2较远的镜像对通量的贡献弱,该通量接近I1单独作用在c2中产生通量的4 倍。故背靠大面积铁氧体材料平行线圈c1与c2的互感M∞Fe可近似为无铁氧体时互感Mair的4 倍,Mair可按式(12)进行数值计算[11]。 式中:μ0为真空磁导率;φ1、φ2为积分变量;r0、r分别为两线圈内半径和外半径;a1=δ1/(2π),a2=δ2/(2π),δ1、δ2分 别 为c1和c2的 螺 距,且 满 足(r-r0)/δ1=N1,(r-r0)/δ2=N2,N1、N2分别为c1和c2的匝数。 对于实际应用中的平面结构LCT,磁芯的面积往往与线圈面积相当,且磁芯磁导率和电导率对互感M的影响相比磁芯面积对M的影响可忽略[6],故M小于M∞Fe,而大于Mair,即: 式(13)可为有限元仿真模型中LCT尺寸的选取缩小搜索范围,但有必要进一步研究对于以下2 种典型磁芯结构,随着传输距离及横向偏移的变化,M与Mair及M∞Fe的关系究竟如何。 圆形平面螺旋线圈LCT的一种典型磁芯结构如附录B 图B1 所示。该LCT 的铁氧体磁芯呈片状,与线圈相固连。其单层密绕线圈的外边缘构成其正方形磁芯的内切圆。将该LCT简称为片状磁芯LCT。 设定这一对平行线圈的r0都为20 mm,r都为100 mm,初级线圈40 匝,次级线圈27 匝,磁芯厚度为10 mm。将按附录B图B1建模得到的有限元软件仿真结果M,以及按式(12)计算得到的相应无磁芯时互感值Mair、线圈背靠大面积片状磁芯时的互感值M∞Fe,整理成如图3 所示的曲面图。其中,计算网格节点设置为:传输距离h自20 mm(即20%r)至100 mm(即r)变化,节点距为10 mm;横向偏移d自0至60 mm(即60%r)变化,节点距为10 mm。为节约计算时间,有限元仿真的网格节点距为20 mm。 图3 片状磁芯LCT的互感仿真结果Fig.3 Simulative results of mutual inductance of flat core LCT 由图3 可知:在h=20%r、d=0 时,片状磁芯LCT互感M达到M∞Fe的74%、Mair的3 倍;随着h和d的增大,M与M∞Fe的差异增加;随着h的增加,M与M∞Fe的差异的增速减慢;随着d的增大,M与M∞Fe的差异的增速增快;当h=r、d=60%r时,M仅为Mair的1.3倍。 进一步的有限元仿真(求解类型必须设为Eddy Current,激励源频率设为100 kHz)研究结果表明,与线圈尺寸相当的铝屏蔽材料[6,12]对片状磁芯LCT 互感的影响较弱。若紧贴图B1 中的磁芯外侧存在厚度为2 mm、面积与磁芯相同的铝板,则当h=20%r、d=0 时,M减小至无铝板时的94%(Mair的2.8 倍);当h=r、d=60%r时,M减小至无铝板时的88%(Mair的1.1倍)。 综上,在已知目标互感与线径,以有限元仿真确定片状磁芯LCT 线圈半径与匝数时,搜索范围宜从目标互感对应的无穷大面积片状磁芯线圈半径和匝数,至目标互感对应的空心线圈半径和匝数,搜索宜起始于目标互感的一半对应的空心线圈半径和匝数。这样,利用式(12)所示半解析解预估,再通过有限元仿真修正,片状磁芯LCT的设计流程如下。 1)对应于hmax和dmax,设定两线圈相对位置。 2)目标互感为Mmin。由于是密绕,线径即是螺距。设定两线圈的r0。在式(8)所示的匝比约束下,依据式(12),编程计算并绘制空心线圈Mair-N1关系曲线,寻找在Mair=Mmin/2 时的N1,确定其对应的外半径ra(ra=r0+N1δ1),同理找到Mair=Mmin/4、Mair=Mmin对应的外半径(rb、rc)。 3)以ra作为初始值建模,根据有限元仿真结果,在(rb,rc)范围内,不断增加或减少N1和r以修正模型,直到片状磁芯LCT的互感仿真结果逼近Mmin。 4)最后必须确认磁芯是否会饱和。 图1 中LCT 初级、次级线圈电流分别与U1、U2成正比[5];磁场分布与磁芯相对位置有关。在hmax与dmax状态下,U2=U2_max;在hmin状态下,平均磁路长度最短,磁路缩短会增加磁芯内平均磁密;在dmax状态,磁场分布最不均衡;由于LCT是松耦合,故磁芯附近的磁密受对侧线圈的影响可忽略,利用文献[13]中图4.16(b)定性分析,磁芯内最大磁密区域出现在LCT磁芯靠近线圈侧的表面;常见的锌锰铁氧体磁芯材料临界饱和磁密是0.3 T。因此观察有限元软件提供的hmin与dmax状态下,磁芯靠近线圈侧表面磁场分布图是否出现磁密超过0.3 T 的区域。若未出现则不同工况下的磁芯均不会饱和,若出现则需增加LCT尺寸或增厚磁芯。 圆形平面螺旋线圈LCT的另一种典型磁芯结构如附录B图B2所示[6],该LCT的磁芯为条形(尺寸为90 mm×20 mm×10 mm),呈辐射状分布。磁芯的分布可稀疏也可稠密,本文仅仿真线圈结构、尺寸同图B1,每盘线圈6 根磁芯的情形。设定磁芯伸出线圈外边缘10 mm。将该LCT简称为辐射状磁芯LCT。 类似图3 的绘制过程,对辐射状磁芯LCT 整理出如图4所示的反映互感值随h与d变化的曲面图。 图4 辐射状磁芯LCT的互感仿真结果Fig.4 Simulative results of mutual inductance of radial core LCT 由图4 可知:在h=20%r、d=0 时,辐射状磁芯LCT 互感M为M∞Fe的49%、Mair的1.9 倍;随着h和d的增大,M与M∞Fe的差异变化趋势同图3;当h=r、d=60%r时,M仅比Mair多7%。 进一步的有限元仿真研究表明,与线圈尺寸相当的铝屏蔽材料对辐射状磁芯LCT 互感的影响较大。若紧贴图B2 中的磁芯外侧存在厚2 mm、构成线圈外接正方形的铝板,则当h和d较小时,M略大于Mair(当h=20%r、d=0 时,M仅为Mair的1.2 倍);当h和d较大时,M小于Mair(当h=r、d=60%r时,M仅为Mair的66%)。 综上,在以有限元仿真确定辐射状磁芯LCT 线圈半径和匝数时,搜索范围宜从目标互感的一半对应的空心线圈半径和匝数,至目标互感2 倍对应的空心线圈半径和匝数,搜索宜起始于目标互感对应的空心线圈半径和匝数。 由于按式(12)计算的效率远高于有限元计算效率[11],故在有限元仿真之前确定LCT 尺寸初始取值和搜索范围,能显著提高LCT设计便捷性。 为验证所提设计方案的正确性,设计了一台样机。技术指标为:Pm=4.5 kW、开关频率f0=100 kHz、U1=700 V、U2_max=400 V、h=60~70 mm、d=0~50 mm。 若取λ1=0.3,λ2=0.2,则由式(1)、(5)、(6)得到Lf1=117 μH、Lf2=57.3 μH、Mmin=83.6 μH、Cf1=21.6 nF、Cf2=44.2 nF;由式(11)得到UCf1m=1 160 V、UCf2m=815 V。实际Cf1和Cf2采用标准件,分别选用标称容量Cf1=20 nF 和Cf2=40 nF、耐压都为3 kV 的圆柱形感应加热专用谐振电容;重新由式(1)确定Lf1=127 μH、Lf2=63.3 μH,又由式(5)确定λ1=0.28、λ2=0.18;由式(6)得到Mmin=99.5 μH。由式(4)得到满载时i1(t)、i2(t)中的基波有效值分别为I11st=I11stm/1.414=7.14 A、I21st_min=I21stm_min/1.414=12.5 A。取LCT 线圈r0=30 mm、J=4 A/mm2,由式(7),LCT初级线圈电流有效值为8 A,选用ϕ0.1×250股丝包线(ϕ1=2.1 mm),次级电流为9 A,选用ϕ0.1×300股丝包线(ϕ2=2.3 mm)。由式(8)得N1∶N2=1.1。为了在hmax=70 mm 与dmax=50 mm 状态下获得Mmin=99.5 μH,在有限元仿真前,先由式(12)缩小LCT尺寸的搜索范围,其中h=hmax=0.07 m,d=dmax=0.05 m,δ1=0.002 1 m,δ2=0.002 3 m,r0=0.03 m;以MATLAB 绘制N1与空心线圈互感Mair的关系如图5所示。 图5 线圈尺寸估算Fig.5 Coil size estimation 由图5 可见:Mair=Mmin/2≈50 μH 对应的N1=N1a为43 匝,故ra=30+43×2.1≈120(mm);Mair=Mmin/4≈25 μH对应的N1b为35 匝,故rb≈104 mm;Mair=Mmin≈100 μH对应的N1c为53匝,故rc≈141 mm。 然后利用有限元仿真修正,以r=ra为初始外半径(此时N1为43 匝,N2=N1/1.1 为39 匝),LCT 的片状铁氧体磁芯选为厚度5 mm、边长250 mm 的正方形,相对磁导率设为3 000,hmax=70 mm、dmax=50 mm 状态下Mmin的仿真结果是98.3 μH。经过进一步优化,最终确定N1为44 匝,N2为40 匝,r=122 mm,相应地Mmin=106 μH。 制作出LCT,测得hmax与dmax状态下L1_min=440 μH(仿真值422 μH),L2_min=358 μH(仿真值348 μH),而Mmin=106 μH;hmin=60 mm、d=0时,L1_max=458 μH(仿真值437 μH),L2_max=373 μH(仿真值360 μH),而Mmax=180 μH(仿真值180 μH)。将L1_max与L2_max代入式(1),得到C1=7.64 nF、C2=8.18 nF,由式(7)、(9)得到C1、C2电压应力分别为2.25 kV 和2.53 kV,确定C1和C2分别以7个和8个耐压为5 kV、容量为1 nF的圆柱形聚丙烯薄膜谐振电容(标准件)并联而成。 将Mmax=180 μH 代入式(2),得到U2_min=236 V,再由式(4)得到I21st_max=I21stm_max/1.414≈21.2 A。确定Lf1和Lf2分别选用ϕ0.1×200股与ϕ0.1×500股丝包线,在PQ4040 磁芯骨架上绕制(Lf1可使用更小的PQ3535磁芯骨架,但考虑到后级Boost 变换器也用到PQ4040磁芯骨架,为了减少物料种类,故牺牲体积)。 将LCT两线圈电流幅值(ILCT_Pm=8×1.414≈11.3(A)与ILCT_Sm=9×1.414≈12.7(A))作用于hmin=60 mm与dmax=50 mm状态的仿真模型,得到2片磁芯靠近线圈侧的表面最大磁密为2.4 mT,远小于前述的0.3 T,故排除磁饱和的可能性。 将制作的LCT 与所选用的其他元件按照图1 搭建成样机,如附录B 图B3所示。WPT 变换器样机包括逆变电路、谐振补偿电容与电感、LCT 以及整流电路,后级的Boost 变换器与整流电路共用一块电路板。其中LCT 的片状磁芯是由厚5 mm 的小块铁氧体材料拼接而成的(总面积为250 mm×250 mm),线圈与磁芯由环氧树脂浇注在铝壳内;Boost 变换器采用2路交错并联结构;样机中所有的MOS都采用SiC器件C2M0280120D,所有的二极管都采用SiC 器件GS40120KQ2;U1=700 V 为充电模块SR750-20 的输出,U2为后级Boost 变换器的输入,Boost 变换器的负载为大功率滑线变阻器。控制屏的作用是设置与监测运行参数,被监测的运行参数除了U1、U2、I1、I2,还包括Boost变换器的输出电压与电流、逆变与整流电路板散热器温度,这些参数由模拟采样电路采集,经28035 处理器处理后与控制屏通信,其中采样电路采用高精度运放OP2177,直流电流的采样使用了ACS712ELCTR-20A 霍尔电流传感器(测量相对误差小于1.5%,内阻为1.2 mΩ)。 设置如下2 种工况:①工况1 为h=hmax=70 mm、d=dmax=50 mm、U2=400 V;②工况2 为h=hmin=60 mm、d=dmin=0、U2=225 V。2 种工况下u1(t)、u2(t)、i1(t)、i2(t)波形如图6所示。 图6 谐振网络电压与电流波形Fig.6 Waveforms of voltage and current in resonant network 由图6 可知,2 种工况下,逆变电路的所有开关管都能实现ZVS,WPT 变换器输出电流I2分别为11.1 A 和20.2 A,输出功率PO=U2I2分别为4 440 W 和4545 W,输入电流I1分别为6.55 A 和6.73 A,WPT 变换器的效率η=PO/(U1I1)分别为96.8%和96.5%。 分别保持上述2 种工况对应的LCT 相对位置,降低U2从而降低PO,得到η随PO变化的规律如附录B 图B4 所示。由图可见:效率与传输功率正相关;在样机性能指标规定的h和d变化范围内,对于相同的功率,当h和d较小时效率相对更低,即WPT 变换器总损耗更高(详细的损耗分析见附录C)。在图B4中各测量点,逆变电路的开关管也都能实现ZVS。 以上实验数据与波形表明,本文方案设计的谐振网络可在宽范围实现逆变电路开关管ZVS。所设计出的LCT功率传输能力达到预期。对比其他文献中的样机:文献[5]中样机在20 cm 距离、最大31 cm横向偏移时传输功率为7.7 kW,开关频率为79 kHz,最大效率为96%,λ1、λ2分别取0.14、0.16,其DD线圈LCT 外形是60 cm×80 cm 的矩形;文献[6]中样机在15 cm 距离、无横向偏移时传输功率为3.3 kW,最大15 cm 横向偏移时传输功率为1.8 kW,开关频率为85 kHz,最大效率为93.6%,λ1、λ2分别取0.23、0.43,其辐射状磁芯LCT 初级、次级圆形线圈直径分别为60 cm、30 cm;文献[7]中样机在15 cm距离时传输功率为6.6 kW,开关频率为85 kHz,最大效率为92.4%,λ1、λ2分别取0.52~0.77、0.82~1.22,其方形线圈LCT初级、次级外形分别为67 cm×54 cm、32 cm×32cm 的矩形。本文样机因应用场景需求,在传输距离、横向偏移、传输功率、开关频率等方面与上述文献中的样机有所不同,但最大效率超过96%。综合考虑LCT尺寸和效率两方面,本文样机在性能上不劣于上述文献中的样机,而本文样机的设计方法更具有便捷性。 本文提出了一种适用于双边LCC 补偿WPT 变换器的谐振网络电参数设计方案,可依据额定传输功率、开关频率等约束条件,确定包括LCT在内的谐振网络电参数。提出了一种适用于该拓扑的圆形平面螺旋线圈LCT尺寸设计方案。通过将传输距离和横向偏移大范围变动时,LCT 互感有限元计算结果与2 种特殊情形半解析解对比,为在已知最大传输距离、最大横向偏移及其对应的互感时LCT 尺寸的估算提供了理论依据,克服了目前有限元仿真中存在的盲目性。样机实验验证了本文方案的正确性。 附录见本刊网络版(http://www.epae.cn)。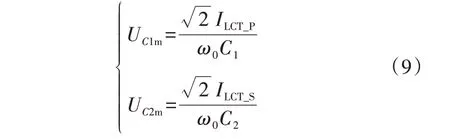
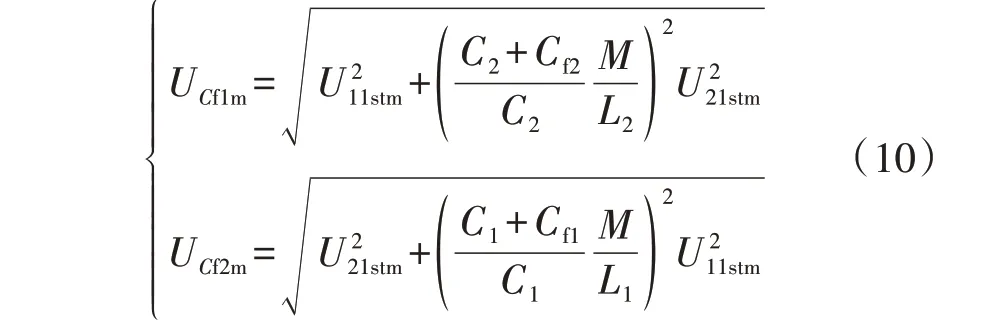
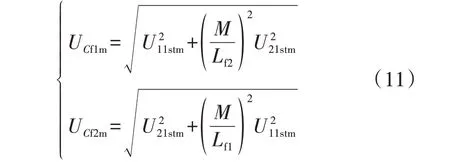
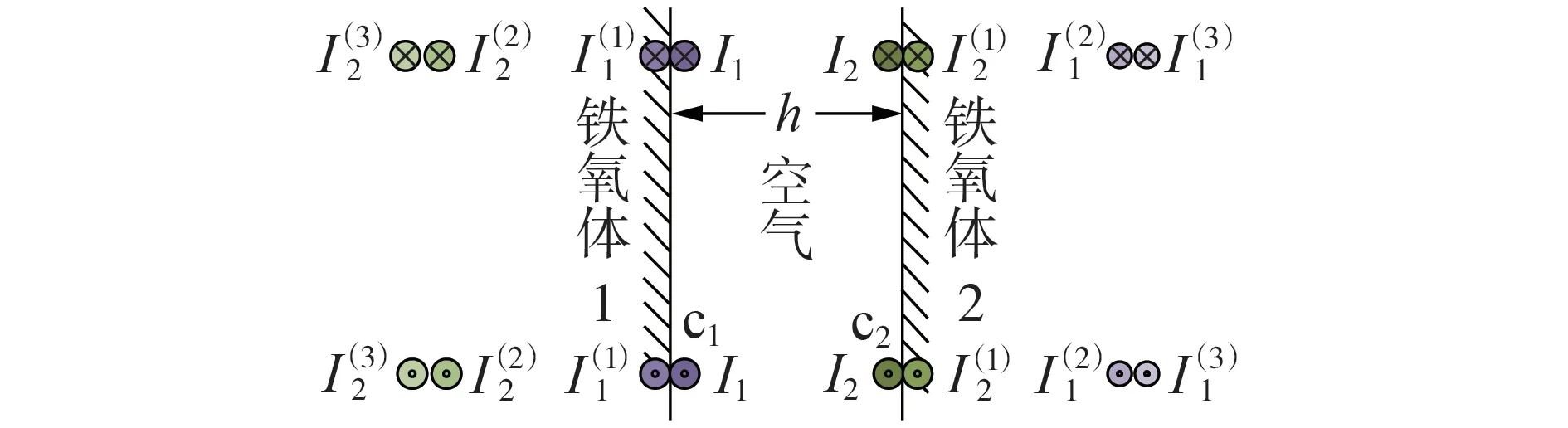
2 带磁芯圆形平面螺旋线圈LCT设计
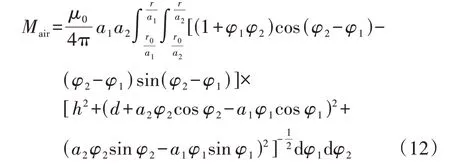
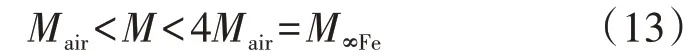
3 样机设计与实验结果
3.1 样机谐振网络设计
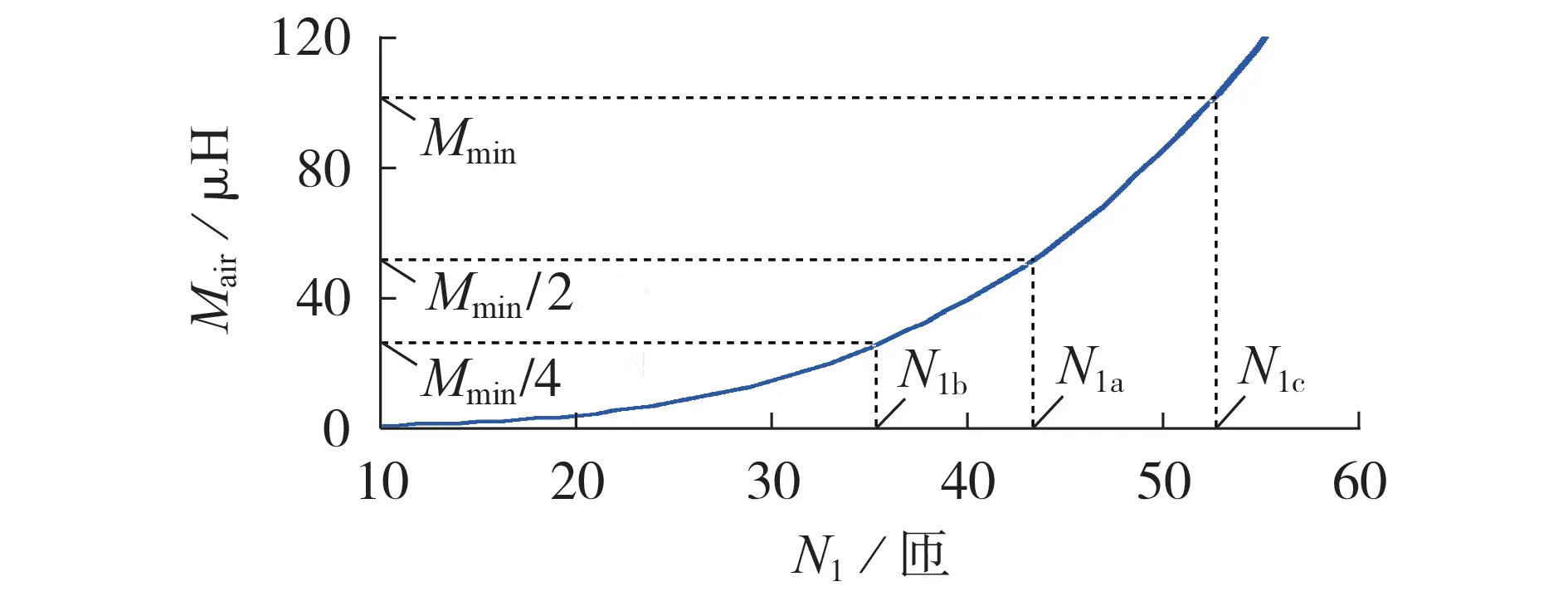
3.2 实验结果
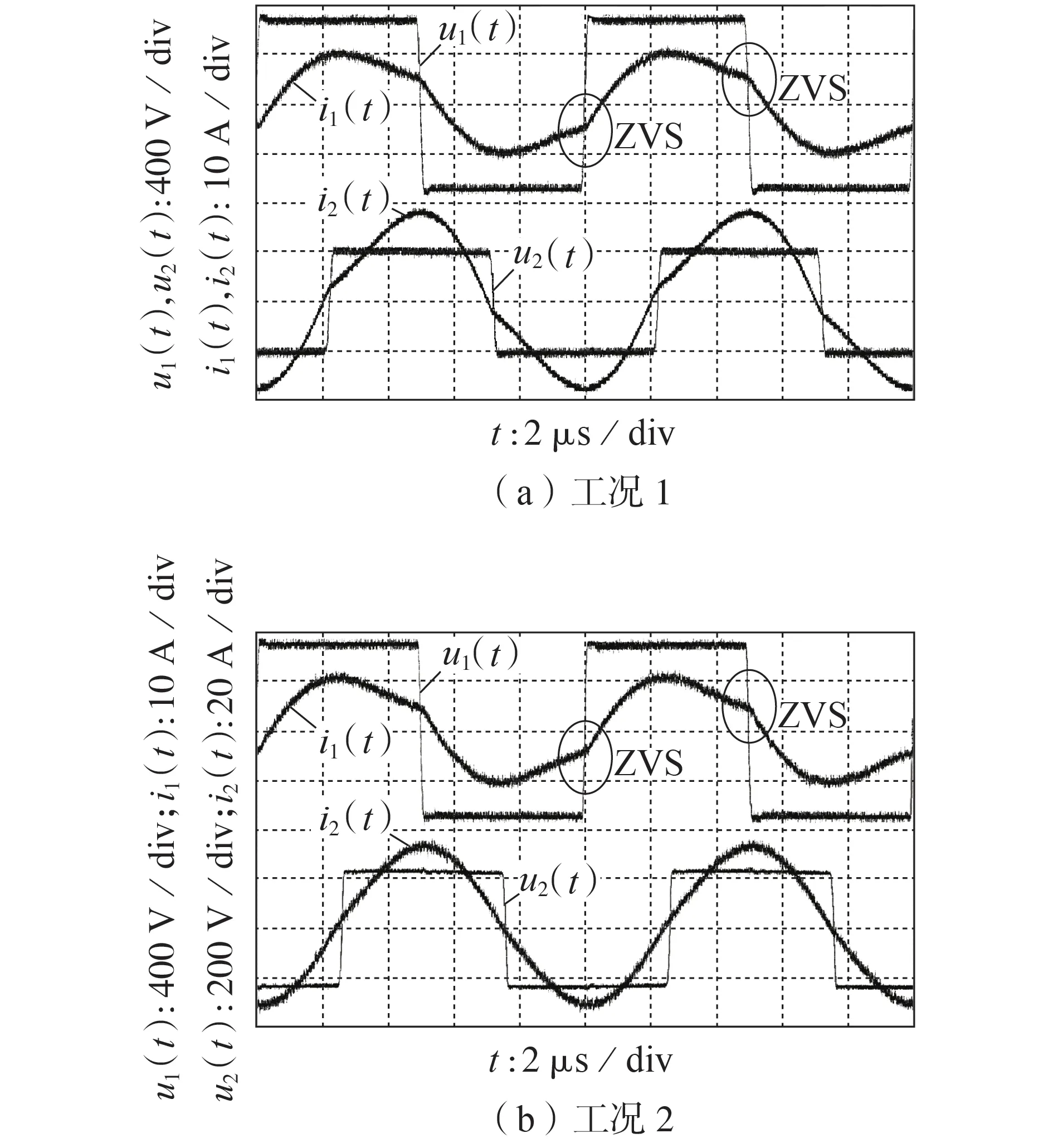
4 结论
