并网VSC系统正阻尼时的一类切换型振荡分析

2022-06-15薛安成汪云涛乔登科王永杰付潇宇

电力自动化设备 2022年6期

薛安成，汪云涛，乔登科，王永杰，付潇宇，2

（1. 华北电力大学新能源电力系统国家重点实验室，北京102206；2. 国网湖南省电力有限公司检修公司，湖南长沙410007）

0 引言

源-网-荷侧多样化电力电子装置的应用极大地改变了现代电力系统的运行方式和动态特性［1］。含大规模电力电子装置的电网呈现出新的稳定形态并产生新的失稳问题［2］，其中由换流器引发的振荡失稳问题引起了学者的广泛关注。

电力电子装置并网后产生的次同步振荡可分为负阻尼振荡、光滑的强迫振荡和切换型振荡［3］。现有研究大多关注小干扰下的负阻尼振荡，即当系统或控制参数变化时在次／超同步振荡模式下系统阻尼会变为负值，引起单一频率的发散的局部振荡［4-7］，而对非线性切换环节引发／参与的切换型振荡研究相对较少。目前，非线性切换环节引发／参与的振荡研究主要包括计及限幅等非线性切换环节的振荡近似分析等效建模以及限幅等非线性切换环节造成系统振荡失稳的机理研究2个方面。

在计及限幅等非线性切换环节的振荡近似分析等效建模方面，现有文献主要采用描述函数法分析换流器控制中的非线性切换环节对振荡动态的影响，其基本思想是利用基波响应代替非线性切换环节，从而将所分析的系统在频域内近似为线性系统［8］，在时域内近似为光滑系统。如：文献［9］提出大信号阻抗模型（LSIM）的概念以分析较大幅值扰动下系统的动态特性，并提出加入非线性切换环节改变LSIM特性以抑制系统振荡的措施；文献［10］基于描述函数理论，利用等效饱和增益表示脉宽调制（PWM）饱和状态，建立电压源换流器（VSC）的LSIM，解释了非线性切换环节引发／参与的切换型振荡所产生的频率和幅值偏差问题；文献［11］和文献［12］分别考虑了直驱风电机组电压限幅和电流限幅环节，建立了包含非线性、线性限幅环节的传递函数，通过广义奈奎斯特判据判断系统的稳定性，相比小扰动模型的传递函数能更精确地估计系统的振荡幅值与频率。

在限幅等非线性切换环节造成系统振荡和失稳的机理研究方面，主要考虑如下2 个方面的问题：一是考虑限幅／切换作用导致系统失去平衡点，造成小扰动失稳或者暂态失稳，如文献［13］分析了逆变器并网系统切换至低电压穿越控制策略时系统的复杂振荡失稳形式，文献［14］基于换流器的虚拟功角（VPA）特性分析了大干扰下由电流限幅导致的失稳；二是切换或者限幅导致的切换型次同步振荡问题，如文献［15-16］基于非光滑分岔理论和时域仿真研究了风电参与的切换型次同步振荡现象，文献［17］建立了并网VSC 系统的12 阶模型，分析了由电流限幅引起的切换型振荡现象，并说明其来源于切换时系统特征值的变化。如果在振荡过程中某些非线性条件（如电流持续达到限幅值等）导致系统被限制在某一流形上，则可按照微分动力学理论，基于降维的流形的数学模型分析该系统的振荡模态，然而上述数学模型的物理意义不够明确，对于实际系统描述的可信度有待进一步研究。

本文基于电流持续达到限幅值后的降阶物理系统进行振荡分析。首先建立了考虑锁相环、电流内环及直流电压外环等控制环节的并网VSC 简化模型。其次分别从数学降阶和物理降阶角度，研究了正阻尼下的电流达到限幅值后引发的切换型振荡机理。分析表明该类切换型振荡近似模型可对应于无平衡点但有极限环的数学降阶系统（MROS）以及具有负阻尼特性平衡点的物理降阶系统（PROS）。最后讨论了PROS 与原系统中振荡产生原因的关联性。上述工作有助于进一步理解非线性限幅环节对系统振荡的影响。

1 并网VSC系统时域模型

并网VSC系统拓扑结构及控制结构见附录A图A1。换流器包括机侧换流器和网侧换流器，本文将机侧换流器等效为恒功率负载，网侧换流器控制结构中包含直流电压外环、电流内环及其锁相环控制。限幅环节考虑对系统振荡动力学特性影响最大的d轴电流参考值idref［18］。忽略PWM 环节，可认为输出电压参考值等于实际值。

系统的状态空间方程（各物理量均为标幺值）的推导过程如下。直流电容的微分方程为：

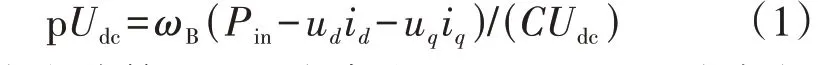
式中：p 为微分算子；Udc为直流电压；ωB=2πf0为角频率基准值，f0为基频；C为直流电容；Pin为输入功率，为恒定值；ud、uq和id、iq分别为网侧换流器出口电压u和电流i的d、q轴分量。直流电压外环通过比较直流电压实际值与参考值，经比例积分（PI）环节输出d轴电流参考值idref，直流电压外环控制的微分方程为：

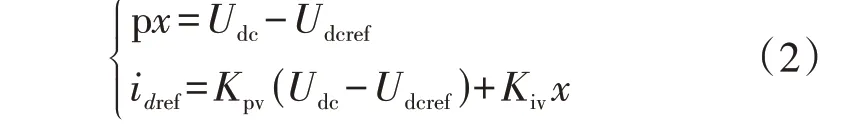
式中：Kpv和Kiv分别为直流电压外环比例系数和积分系数；Udcref为Udc的参考值；x为附录A图A1所示并网VSC 控制结构中的中间变量。设q轴电流参考值iqref为定值，电流内环通过比较电流实际值与参考值，经PI 环节和补偿项后输出电压参考值。忽略d、q轴网侧换流器出口电压的交叉耦合项［19］，选取ud、uq为状态变量，采用相同的电流内环比例系数Kpc和积分系数Kic，电流内环的微分方程为：

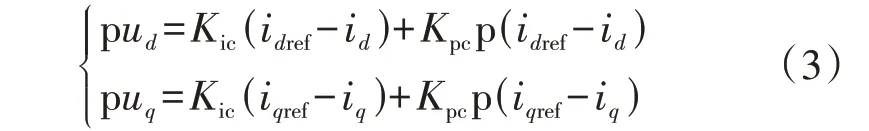
系统中存在2 个坐标系：一是锁相环d′q′坐标系，其d′轴定向于d轴并网点电压utd，且以锁相环输出角频率ωpll旋转；二是电网电压dq坐标系，其d轴定向于d轴电网电压ugd，且以同步角频率ω1旋转。上述2 个坐标系的关系如图1 所示，图中φ为d轴、d′轴间的夹角。锁相环的微分方程为：

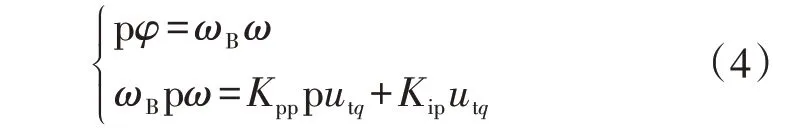
式中：ω=ωpll-ω1；Kpp和Kip分别为锁相环比例系数和积分系数；utq为q轴并网点电压。由图1 可得ugd、ugq转化到锁相环d′q′坐标系后的变量关系如下：

图1 坐标系示意图Fig.1 Schematic diagram of coordinate system

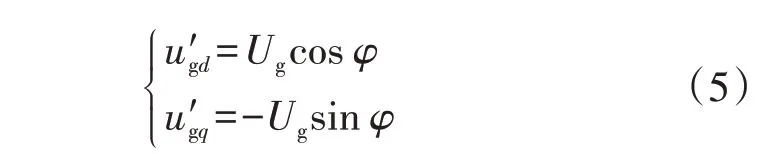
式中：Ug为电网电压幅值分别为d、q轴电网电压转化到锁相环d′q′坐标系后的变量。主回路在锁相环d′q′坐标系下的电流微分方程为：

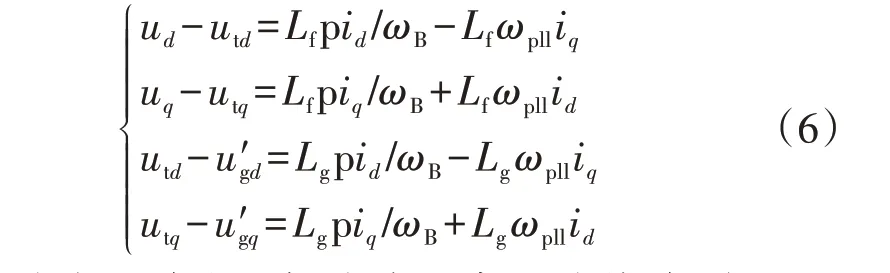
式中：Lf为主回路出口侧滤波电感；Lg为线路、变压器及电网电抗的等效电感。联立式（1）—（6）可得并网VSC 系统包含状态变量（φ，ω，ud，uq，id，iq，x，Udc）的8阶简化模型，各变量的微分方程见附录B式（B1）。

2 小扰动稳定及参数影响分析

并网VSC系统中平衡点稳定性由对应雅可比矩阵J的特征值决定。进一步，对于上述模型，可得雅可比矩阵表达式如附录B式（B2）所示。并网VSC系统参数如附录C 表C1 所示，系统的平衡点和特征值如附录C 表C2所示。由表C2可知，系统含有4个平衡点AEQ1—AEQ4，其中：AEQ1为系统稳定运行点；AEQ2—AEQ4为含有一个正实部特征值的不稳定鞍焦点，由其对应的状态变量值（φ，id）可知，此时VSC 的输出功率过大，导致系统不能维持稳定运行［20］。

稳定运行于平衡点AEQ1的并网VSC 系统主要包含4 种振荡模式，各振荡模式下的振荡主导环节、振荡频率、阻尼比以及引起振荡的参与变量如表1 所示。表中，ed、eq分别为电流内环输出电压的d、q轴分量。

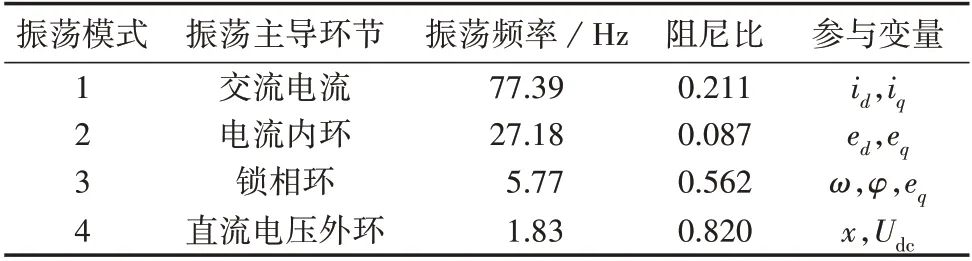
表1 平衡点AEQ1下并网VSC系统的4种振荡模式Table 1 Four kinds of oscillation modes of gridconnected VSC system under equilibrium point AEQ1

进一步，分析振荡模式1—3下并网VSC系统随单一参数变化的系统稳定性变化情况（振荡模式4始终稳定，直流电压外环参数对并网VSC 系统的稳定性无明显影响，此处均不做分析）。当改变某一参数时，维持其他参数为表C1 中的初始值不变，分析结果如表2 所示。表中，“↓”、“↑”分别表示该参数相较于表C1 中原始参数值的减少、增加情况，其后数值表示各振荡模式下系统变为不稳定运行时的参数临界值；Lg为标幺值，后同。由表2可知，虽然振荡模式1、3 下个别参数的变化会影响并网VSC 系统的稳定运行，但振荡模式2 下系统的稳定性受诸多参数的影响，因此振荡模式2 为并网VSC 系统中受参数变化影响的主要不稳定振荡模式。

表2 参数变化对振荡模式的影响Table 2 Influence of parameter variations on oscillation modes

3 正阻尼时电流限幅导致切换型振荡现象

当系统运行于稳定运行平衡点且系统呈正阻尼状态时，在遭受小扰动后各电气量的运行曲线会逐渐收敛至平衡点；在系统遭受大扰动后，为限制设备过流、过压可在电流内环控制器中加入电流限幅环节，电流达到限幅值后控制环节进行动态切换，形成系统的切换型振荡现象［3］。

设Kpp=4.8，其他参数均保持表C1 所示数值不变，设idref的上限值idmax=0.9 p.u.，为模拟系统遭受大扰动后的初始点，设置初值为距离平衡点较远的某一数值，对简化系统数学模型进行数值积分可求得系统各状态变量的时域响应。加入限幅前后ω、ud和idref的时域响应对比如图2 所示，图中纵轴变量为标幺值。由图可知：未加入限幅时，电气量波形最终稳定于平衡点，系统收敛，这表明此时系统为光滑的正阻尼系统，与特征值分析结果一致；加入限幅后系统变为非光滑系统（平衡点附近为局部光滑正阻尼系统），在相同初值下系统出现振荡，振荡频率为6.6 Hz，此时idref在0.1 s左右达到idmax后维持不变。

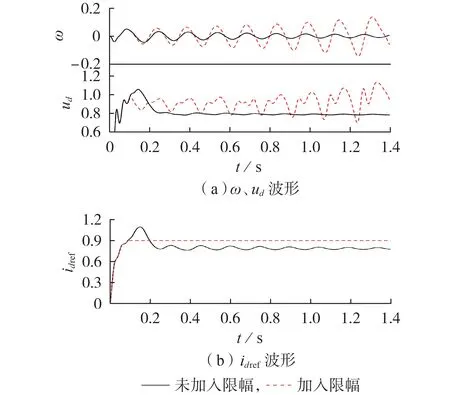
图2 加入限幅前、后系统时域响应对比Fig.2 Comparison of time domain response of system before and after adding limitation

综上所述，限幅环节对系统的动力学特性影响显著。加入限幅后，原正阻尼的系统产生振荡，此时无法通过原系统平衡点处的特征值描述系统的稳定性（平衡点的吸引域因限幅的存在而发生剧烈变化，吸引域减小）。值得注意的是，该振荡在大扰动和限幅的共同作用下产生（若为小扰动，则无需限幅，系统为局部光滑系统），是一种切换型振荡［3，15］。

4 基于MROS的切换型振荡分析

4.1 加入限幅的MROS分析

本节从数学降阶角度初步分析正阻尼下加入电流限幅环节后引发的并网VSC 系统切换型振荡机理。当电流达到限幅值并保持不变时，系统自由度由8维降为7维，即并网VSC系统数学模型变为含状态变量（φ，ω，ud，uq，id，iq，Udc）的7 阶简化模型。若此时MROS存在平衡点，则其平衡点的数学表达式为：

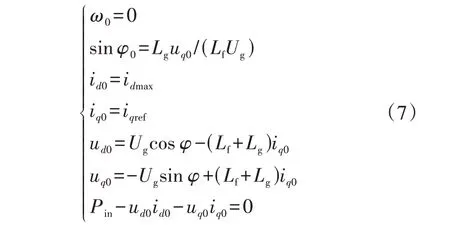
式中：下标0 表示各电气量的稳态值。由式（7）可知，当系统受大扰动后，直流电压外环控制失效，即pUdc≠0，Udc无稳态值，进而导致ud不存在稳态值，故该MROS不存在平衡点。

值得注意的是，关于系统稳定性的研究大多针对存在平衡点的系统，而针对无平衡点但存在极限环系统的稳定性研究较少，目前大多针对3 阶系统或可等价为2、3阶的高维系统进行研究，鲜有考虑4阶系统的情况，如文献［21］研究了考虑增强型死区时无平衡点但存在稳定极限环4 阶系统的稳定性。7 维系统极限环的存在性还需进一步证明，故本文不再考虑通过MROS 分析电流达到限幅值后系统的稳定性，而考虑基于PROS进行分析。

4.2 切换型振荡产生的参数条件

从分岔角度看，随着参数的变化，切换型振荡的发生对应于系统发生非光滑分岔［3］。当改变单一参数时，保持其他参数为初始值不变，并网VSC系统发生非光滑分岔的单一参数临界值如表3 所示，表中Kpp、Kpc、Kic、Kpv小于其临界值时系统发生切换型振荡，Kip、Kiv、Lg大于其临界值时系统发生切换型振荡，且当Lg改变时，系统平衡点发生变化，而其余控制参数改变时，平衡点不变化。

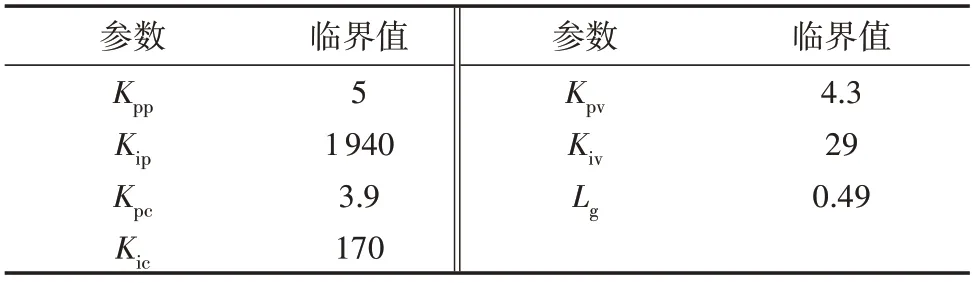
表3 切换型振荡发生时并网VSC系统参数临界值Table 3 Critical values of parameters for grid-connected VSC system when switched oscillation occurs

5 基于PROS的切换型振荡分析

5.1 加入限幅的PROS分析

当电流初始值与参考值存在偏差时，直流电容两端功率不平衡，造成直流电压偏差，直流电压通过直流电压外环控制调节idref输出，进而维持直流电容的两端功率平衡；当系统受大扰动影响（电流初始值较大）导致较大的直流电容两端功率不平衡量出现时，直流电压外环控制调节输出的idref达到限幅值，这意味着此时直流电压外环的调节能力受设备过流能力限制，难以维持直流电容两端的功率平衡，进而导致直流电压进一步升高，该过程中直流电压的动态响应如图3 所示，图中Udc为标幺值。随着直流电压的升高，输出的idref进一步增大，达到限幅值后维持idmax不变，此时直流电压外环控制失效，相当于直流电容和直流电压外环控制环节与系统其他部分解耦，因此当idref=idmax时，原系统的拓扑结构和控制框图等效为附录D 图D1 所示的PROS，即忽略直流电容和直流电压外环控制的动态响应。

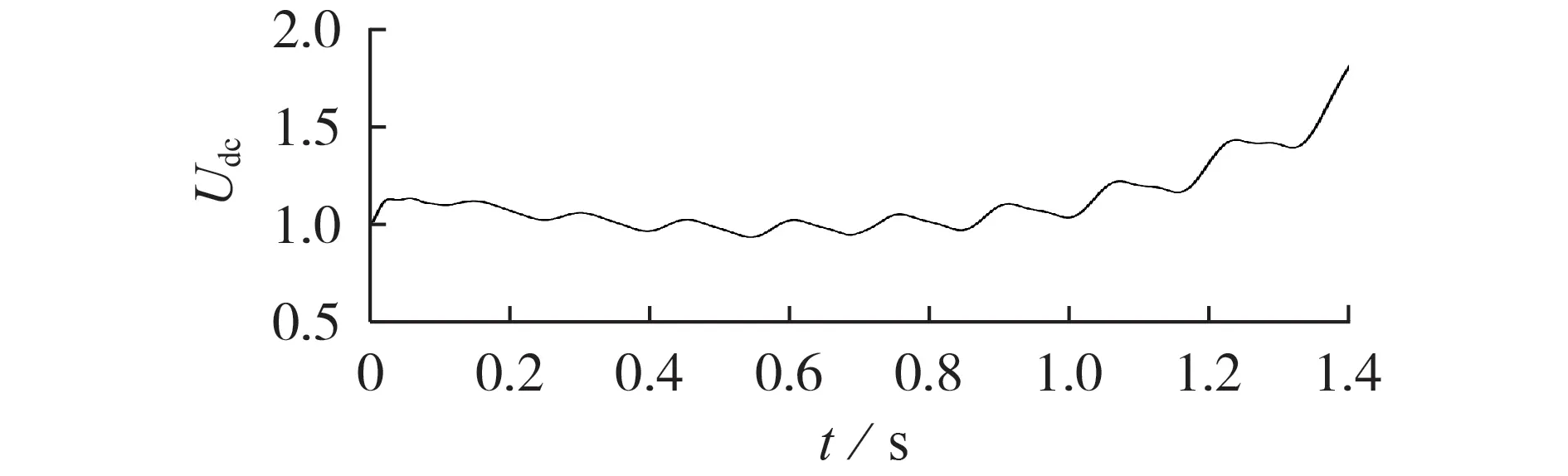
图3 电流持续达到限幅值时Udc时域图Fig.3 Time domain diagram of Udc when current reaches its limitation

5.2 PROS的稳定性分析

取Kpp=4.8，其他参数不变，当idref=idmax时可得4种振荡模式下PROS 与原系统的特征值对比结果见表4。加入限幅环节前并网VSC 系统稳定运行于平衡点AEQ1，加入限幅后大扰动导致系统电流达到限幅值，将原系统等效为附录D 图D1 所示的PROS。由表4可知，PROS 存在不稳定的振荡模式3，故此时系统不稳定出现振荡现象。

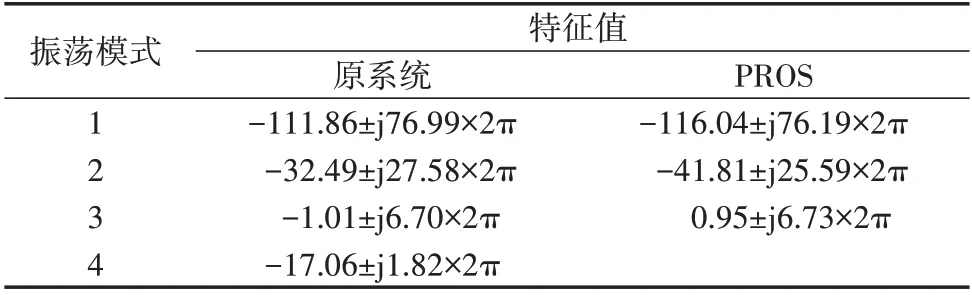
表4 4种振荡模式下原系统与PROS特征值对比Table 4 Comparison of eigenvalues between original system and PROS under four kinds of oscillation modes

基于PROS 对并网VSC 系统进行稳定性分析，系统的振荡频率为6.73 Hz，而原系统的振荡频率为6.6 Hz，两者基本一致，验证了基于PROS 进行系统稳定性分析的准确性。此时系统运行于振荡模式3下，并出现次同步频率的振荡现象。进一步分析振荡模式3 下PROS 的根轨迹随idref的变化情况，如图4所示。由图可知，随着idref从0.5 p.u.逐渐增大，振荡模式3 下PROS 的根轨迹逐渐右移，阻尼比减小，并在idref=0.67 p.u.时到达右半平面，即振荡模式3下系统变为不稳定。上述仿真结果表明随着idref的增大，PROS 的稳定性变弱，当idref=idmax=0.9 p.u.时，PROS呈现负阻尼特性。

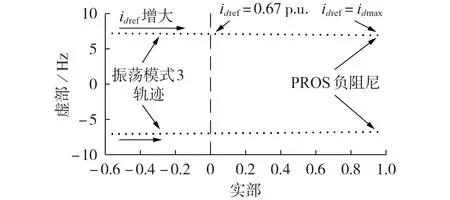
图4 idref变化时的振荡模式3轨迹Fig.4 Trajectory of Oscillation Mode 3 when idref changes

综上，大扰动下正阻尼时并网VSC 系统的切换型振荡现象可解释为：大扰动使得具有稳定运行点的系统电流达到限幅值，等效降阶为具有负阻尼平衡点的PROS，从而产生发散振荡。

5.3 PROS产生振荡的参数条件

分析PROS 平衡点处雅可比矩阵的特征值，当改变单一参数时，保持其他参数为初始值不变，振荡模式3 下PROS 发生Hopf 分岔变为振荡状态的单一参数临界值如表5 所示，表中Kpp、Kpc、Kic小于其临界值时系统发生Hopf分岔，Kip、Lg大于其临界值时系统发生Hopf 分岔，且当Lg改变时，系统平衡点发生变化，而其余控制参数改变时，平衡点不变化。

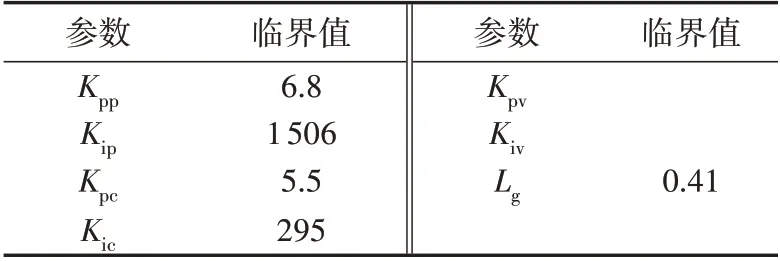
表5 发生Hopf分岔时PROS参数临界值Table 5 Critical values of parameters for PROS when Hopf bifurcation occurs

5.4 原系统和PROS中振荡产生原因的关联性讨论

结合前文所分析的振荡产生原因，可进一步推测原系统和PROS 产生振荡条件之间的关系。对比表3、5 可知，产生振荡现象（发生分岔）时原系统和PROS 对应的参数变化具有相同趋势，如：Kpp越小，越容易产生振荡；发生切换型振荡对应的非光滑分岔时原系统参数临界值小于发生Hopf 分岔时PROS参数临界值，即发生切换型振荡的参数范围小于PROS发生负阻尼振荡的参数范围，这说明原系统出现切换型振荡（非光滑分岔）的前提是PROS 出现振荡模式3下的Hopf分岔。

所提PROS 按照物理降阶规律，忽略直流电压外环控制，将8 阶系统降为6 阶系统，仅通过物理近似未进行数学推导，同时根据分析结果，发生分岔时PROS参数值与原系统存在一定差异，故所得振荡模式3 下PROS 发生Hopf 分岔变为振荡状态的单一参数范围相较于原系统具有一定的局限性。需要说明的是，表3所示参数临界值会随着所设置的直流电压外环控制参数初值（PROS 不含该参数）的变化而变化，进而在理论上也可由直流电压外环与电流内环控制参数的协调优化来避免该切换型振荡的发生。