几类具有多项式势的可积系统的耦合常数变形

方东丽，章 海

（安庆师范大学 数理学院，安徽 安庆 246133）

从已知的经典可积哈密顿系统出发构造新的可积系统是一种常见的研究思路。由Hietarinta等[1]引入的耦合常数变形（CCM）是一种在经典可积系统之间变换的方法，适用于任何具有势函数的哈密顿系统。它将一个哈密顿系统变换成另一个哈密顿系统，并保持可积性，这样就可以生成新的可积系统。新系统的哈密顿量表达式一般来说是任意的，但是采取合适的正则变换可以将其化简成标准的自然哈密顿系统的形式，即哈密顿量为动能与势能之和的形式。例如，Holt系统在几组特定的参数下是可积系统，利用CCM可以得到新的系统，再借助于正则变换即可变成可积的Henon-Heiles系统[2]，因此得到了Henon-Heiles系统和Holt系统之间的对偶[1-4]。CCM在可积和超可积系统研究中有很多应用，可以从已知的平坦空间上的二次超可积系统生成非平坦空间上的二次超可积系统。然而，在高维情况下，CCM并不能保持守恒量的阶数。为了从这个一般的变换得到有用的结果，需要限制变换作用的范围或条件。Kalnins等[5]研究了部分势能项消失情况下的CCM，此时也称为雅可比变换，这种特殊形式的CCM将哈密顿系统的n阶守恒量转化为新系统的n阶守恒量，但并不改变守恒量的阶数。CCM已被有效地应用于构造新的高阶超可积系统，可以将TTW系统（简谐振子势的超可积形变族）映射为PW系统（超可积的开普勒-库仑势形变族）[6]。

非退化的二次超可积系统可以通过CCM变换从常曲率空间中的二次超可积系统得到[7]。CCM以一种简单的方式修改了超可积系统的泊松代数，使得我们可以将非退化的二次超可积系统分成7个等价类，在同一类的系统可以运用CCM和伸缩变换来相互转化[8]。文献[9]引入了经典和量子可分系统的Stackel变换，Stackel变换和CCM一般情况下是不相同的，但当限制于二阶超可积系统之间的转换时，它们是一致的。Stackel变换对经典和量子超可积系统都有定义，被广泛且有效地应用于二阶超可积系统的分类。文献[10]提出了一族具有多项式势能的平面可积系统，其中每个系统都在抛物坐标下可分[11]。本文通过将这些势能线性组合起来，得到非齐次多项式势能。这些系统具有适合于用CCM方法处理的形式。我们考虑这些系统的CCM，分析所获得的新系统的可积性质和几何性质。

1 耦合常数变形

耦合常数变形是一种非正则变换，是通过原哈密顿系统中的耦合常数与能量做交换来获得新系统，且保持系统的可积性[1,12-14]。原系统的守恒量是确保新系统可积的关键。考虑一个n维经典哈密顿系统

其中，T是动能项，U、V是关于坐标q=(q1,q2,q3,…,qn)的势能项，α是与其独立的任意耦合常数。

列出系统（1）的哈密顿-雅可比方程T+V-αU=E，再解出耦合常数α来获得新系统：其中，耦合常数和哈密顿量的角色进行了互换，这样的变换称为耦合常数变形。假设对于参数α的每一个值，系统都有守恒量I(α)，它与H是对合的，{H,I}=0。CCM的一个显著特征是新守恒量与新哈密顿量的关联映射，即通过CCM转换后的函数J=I(G)与新哈密顿量G也是对合的，{G,J}=0，从而保证了新系统是可积的。由{I(α),H}=0得{I(α),T+V-αU}={I(α),T+V}-{I(α),αU}=0，{I(α),T+V}=α{I(α),U}，对任意常数α都成立。又因为

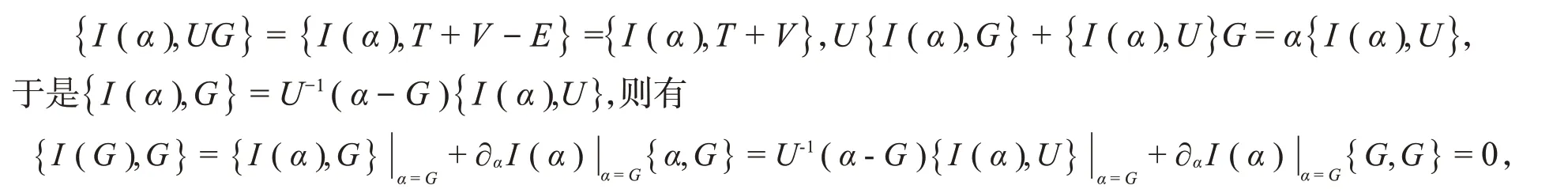
可见J=I(G)确实是新系统（2）的守恒量。

CCM把可积系统变成可积系统，把超可积系统变成超可积系统，我们主要关心的是自然哈密顿系统和它的多项式形式的守恒量。原系统的二阶守恒量I通常关于耦合常数α上是线性的（也可能与α无关），所以它们被转化为新系统的二阶守恒量，即CCM保持二阶守恒量的阶数。然而，一般情况下CCM并不能保持高阶守恒量的阶数。对于一些含有多个耦合常数的系统，选择不同的耦合常数做CCM变换，变换后守恒量的阶数可能会有改变，多项式守恒量甚至会变成动量的有理函数（非多项式）[5]。

2 带组合势系统的耦合常数变形

使用CCM方法时，耦合常数的位置和势能项的结构很重要。本文考虑文献[10]提出的带有如下多项式势的系统：

2.1 V1和V n的组合势

2.2 V2和V3的组合势

2.3 V2和V4的组合势

考虑式（8）中的V和任意Vn的组合，可得组合势能

注新哈密顿函数G3和守恒量J3的二次部分与G2、J2的二次部分分别相等（忽略非零常数因子），函数G3、J3对应的度量、Killing张量、高斯曲率与G2、J2的结果（11）、（12）都相同。

3 结论

CCM在可积系统研究中起着重要作用，系统中势能的加性项结构非常关键。本文对几类带有非齐次多项式势能的可积系统做耦合常数变形处理，获得了新系统的哈密顿函数和守恒量。对于这些对合的守恒量二次项部分对应的度量，计算了其高斯曲率和Killing张量。容易看出，这些新系统定义的空间不是常曲率空间，所以仅用点正则变换不可能把它们变为常曲率空间上的系统。因此，必须采用类似于文献[1]中的一般正则变换，才能把这些系统化为常曲率空间上的可积系统，甚至平坦空间（欧氏空间或闵氏空间）上的系统。另外，本文分析的几个系统势能项只含有一个任意参数，若势能项含有多个任意参数，则可以对原始系统连续地作多次CCM变换，每次变换减少一个参数，最终得到系统的哈密顿量与守恒量的特征，以及它与文献中已有系统之间的联系。