基于大单元教学的高三数学复习课问题链设计

杨进生 李琳 郑敏

摘要：问题链不应该是针对某一课时，而是应该站在大单元教学的角度进行统筹设计。

关键词：高三数学复习课;大单元教学设计;问题链

大家都知道自古数学就有两种形式，一种是中国古代的数学，是以问题解决为主要目标，经典著作《九章算数》就是由246个数学问题及解法汇总而成。另一种是古希腊数学，以公理化的演绎系统为主要特征，大名鼎鼎的《几何原本》就开创了数学理性思维的先河。两者相辅相成，互为补充。然而在高中数学复习中，我们大部分老师当然也包括我都喜欢第二种模式。首先复习基础知识，然后通过例题揭示基本方法，最后通过习题加以巩固。当然这种模式有它自己的优势，比如更易构建学生的知识框架结构，更易培养学生的逻辑思维能力。但他的缺点也很明显，这种模式突出了教师的教，教师的思维固化了学生的思维，对提高学生解决问题的能力是不利的。所以我们在刚复习过的解三角形这一单元中尝试了问题链教学。受到我们以前做的大单元教学设计的启发，我觉得问题链也不应该是针对某一节课时，而是应该站在大单元的角度进行统筹设计。

第一步，在对考纲、高考、教材、学情进行分析之后，初步确定本单元的关键问题。

考纲分析：1、掌握正弦定理和余弦定理，并能解决一些简单的三角度量问题。

2、能够运用正弦定理和余弦定理的知识方法解决一些与测量和几何计算有关的实际问题。

高考分析：近年的全国卷中解三角形一直都是高考的热点问题。它常常和数列交替出现在解答题的第一题中，选填也经常涉及。题目往往与平面向量，三角公式相结合考察，题目常规难度中等。

教材分析：本单元既是初中解直角三角形的延伸，也是三角函数和平面向量知识考察的重要载体。正余弦定理本身揭示了一般三角形中的重要边角关系。在实际测量中有许多应用与社会生活联系紧密，有很强的实践性。

学情分析，现在教的两个班作为文科创新班和文科重点班，本身的数学基础不是太好。又加上当时学习新课时正值网课期间，导致学生对本单元内容本来就掌握不了，后来又遗忘了很多。所以本单元复习的重点是让学生重拾知识，构建解题思路与方法。通过以上4点分析，我初步确定了本单元的两个关键问题：一、什么是正弦定理？余弦定理？他们在解三角形如何应用？二、如何用正弦定理，余弦定理解决实际问题？

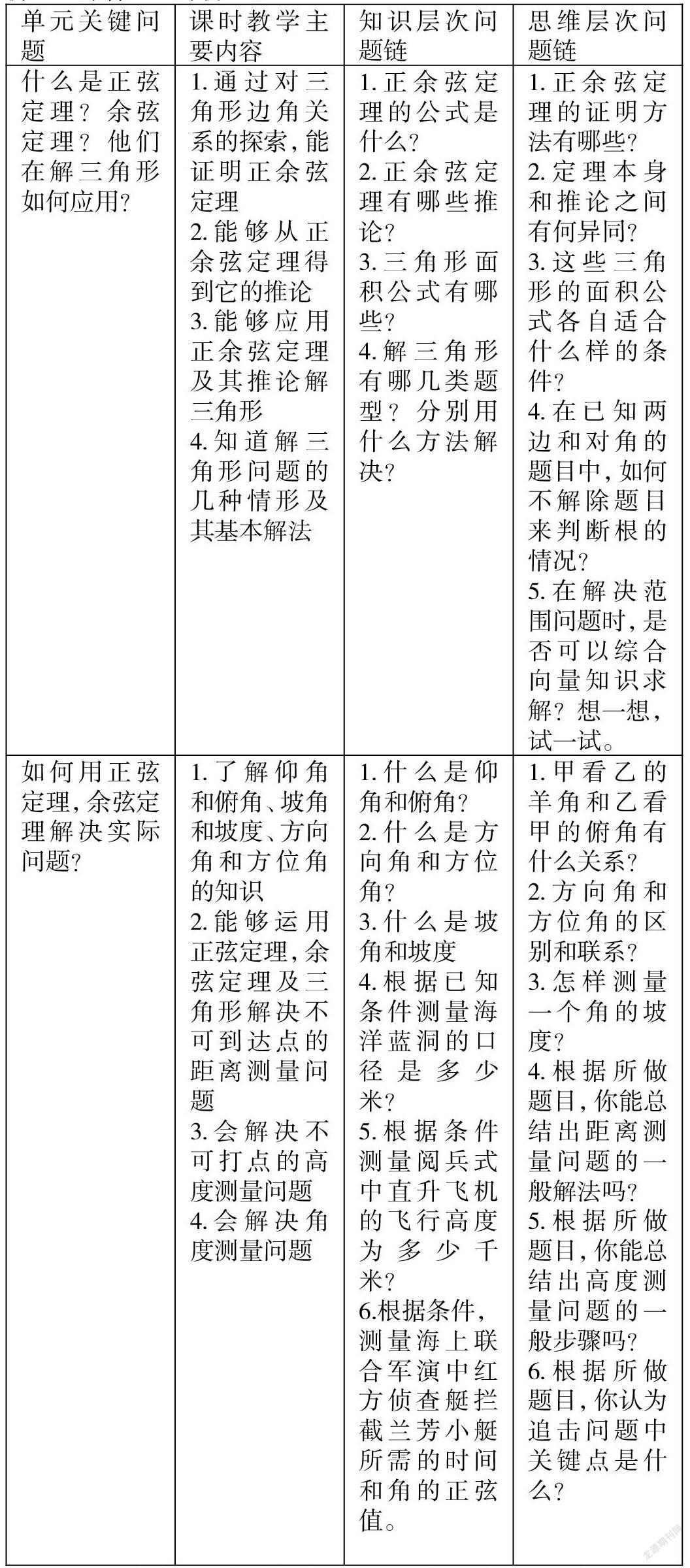
第二步，根据本单元关键问题确定课时教学的主要内容，根据这两个主要问题确立了两个课时及每个课时的四个学习目标。

第三步就到了对每个课时进行问题链设计了，关键就在这个链字上，为什么要链？怎样链？我们说的问题链不是一些问题的简单堆砌，而是一连串有序列、有聯系、有中心、有系统性的教学问题的整合。从形式上看，它是一问接一问，一环套一环;从内容上看它是问问相连，环环紧扣;从目标上看它是步步深入，由此及彼。他的每一问都要使学生的思维产生一次飞跃，像一条锁链，把疑问和目标紧紧连在一起。以下就是我根据目标设计的两个层次的问题链：“知识点”和“思维链”。如果用布鲁姆目标分类法的六个层级来解释，那知识链指向的就是前三个层级：“知道”“领会”“应用”，思维链指向的就是后三个层级：“分析”“综合”“评价”。

最后用数学家哈尔莫斯的一句名言作为结束语，“定理证明，概念，定义，理论公式，方法都不是数学的心脏，只有问题才是。”

课题：本文是河南省教育科学“十四五”规划课题“基于核心素养的高中数学新教材大单元教学研究”（立项编号：2021YB0835）的部分研究成果。

作者简介：杨进生，1968年6月，男，河南信阳，大学本科，郑州市第九中学，高级教师，教育教学。3AFFD750-6C15-4442-8247-83E5B243C7BC