断溶体油藏连通路径智能识别
2022-06-09孔强夫刘坤岩韩东熊培祺
孔强夫 ,刘坤岩 ,韩东 ,熊培祺
(1.中国石化石油勘探开发研究院,北京 100083;2.中海油能源发展股份有限公司工程技术分公司,天津 300450)
0 引言
目前,我国石油产量的70%仍来自老油田,其剩余可采储量依然相当可观。与此同时,老油田经过几十年的开发,总体已进入“双高”(高采出程度、高含水率)开发阶段。高含水油田挖潜的中心任务是提高油藏采收率,提高油藏采收率的关键是准确预测剩余油相对富集区,这类油田的开发成为我国石油界面临的重大挑战。以塔河油田碳酸盐岩油藏为例,该油藏2013年已成为中国最大的碳酸盐岩缝洞型油藏[1-3],年产量达600×104t。该类油藏缝洞储集空间形态多样,分布不均,非均质性强。油藏连通路径识别是开展缝洞储集体动用状况分析、注水(气)效果差异性分析、后期调整对策及注采井网构建的基础。如何表征缝洞型油藏的井间连通结构,已成为科研生产研究的难点。
前人主要通过地球物理与地质手段对缝洞储集体的宏观结构进行研究,同时利用井间干扰试井、油藏数值模拟、地球化学及动态反演等方法在井间动态连通性方面开展了大量的研究工作。但这些研究主要停留在井间连通对应关系及连通程度的定性分析上[4-10]。数字岩心是利用CT扫描的岩心数据对孔隙特征进行分析计算,得到孔隙连通性及分布等参数。提取地震属性得到的油藏孔隙度切片数据,类似于数字岩心中的CT图像处理后得到的孔隙度数据,其大小满足一定的分布规律,因此,可以借鉴数字岩心中的孔隙连通性分析方法,应用于地震孔隙度数据,进而分析油藏井间、层位间的孔隙连通关系。
本文首先利用数字岩心中的图像处理方法(插值、二值化、最大球算法等)对地震孔隙度数据进行处理,保留原始孔隙间的连通路径和几何特征;然后通过离散化达西定律中的流动面积、流动单元渗透率2个参数对流动路径的权值进行赋值,进而建立带有流动路径权值的油藏孔隙连通模型[11-16];最后运用迪克斯特拉(Dijkstra)算法找到孔隙网络中井间地理最短路径和权值最小路径(即优势通道)[17-26]。
1 连通路径智能识别方法
连通路径智能识别方法是基于油田的油藏孔隙度分布数据,通过插值、权值赋值计算,将实际路径根据路径特征进行加权,进行最优路径计算和查找。该方法主要分8步完成。
1.1 读取孔隙度数据文件
地震孔隙度切片原始数据文件是Petrel软件存储孔隙度等数据的数据体文件,采用道的方式对数据进行存储和读取。数据文件通过转码加密,借助外部的程序或者库函数将数据按道读取出来。
1.2 数据间插值
为了细化油藏的孔隙结构和完善孔隙度分布,同时保留孔隙路径的拓扑结构,采用层间插值的方法对油藏孔隙度数据的层间数据进行插值完善,提高数据量,间接提高油藏孔隙度数据分辨率。由于层间数据缺失,故根据不同情况优先推荐反距离插值(IDW)或线性插值方法。图1为2种方法的实际插值效果对比。图1a为使用全三维反距离插值得到的中间像素图像,图1b为使用分片二维线性插值得到的中间像素图像。

图1 2种方法的实际插值效果对比
图1中存在黑色的孔隙流动通道,也存在蓝色的不可流动的无效流动区域。全三维反距离插值会引入不可流动区域的孔隙度值进行插值运算,使得最终图像中黑色有效流动区域被整体参数平均,出现了有效孔隙和无效孔隙的模糊化,图像特征不够明显。而图1b采用分片二维线性插值算法,得到的有效孔隙和无效孔隙的对比较为显著,图像特征明显,与原始图像特征较为接近。
1.3 孔隙阈值剖分
孔隙度数据与图像灰度数据一样,二值化剖分时存在一个最佳的剖分点。对孔隙度数据的统计可以看到,孔隙度分布呈现明显的谷底阈值分布特征,可以采用谷底阈值的方式对孔隙度进行二值化分类。结合图像灰度直方图和油藏孔隙分类理论,每一种油藏具有独有的油藏孔隙分布特征,同时也存在最佳的流动孔隙剖分阈值。采用基于直方图的二值化方法,将地震孔隙度切片原始数据文件中的所有孔隙度值绘制成直方图,寻找其双峰的谷底作为阈值。通过谷底阈值方法二值化后的图像,能够清楚地区分流动路径和非流动区域。还可以使用K值聚类分析或K值聚类分析增强算法对孔隙度进行分类,也能取得很好的分类效果。
1.4 细化提取路径
在保留路径拓扑结构的前提下,对路径进行细化,提取路径的关键特征信息,用单个像素的宽度代替原始路径的半径。细化算法采用模板刻蚀的方法,利用12个像素的矩阵刻蚀矩阵,不断地刻蚀二值化之后的路径区域,直到无法再刻蚀为止,即为最优细化路径。
1.5 生成连通关系
采用中轴变换方法提取了所有连通路径的拓扑结构,借鉴格子玻尔兹曼方法中的邻域和连通关系定义,在二维空间内每一个细化后的可流动像素位置使用8连通的3×3滤波器,对每一个流动像素的邻域进行查找,并保留连通关系。
1.6 建立权值通道
利用达西定律确定线性流动下的渗流规律,得到的基础模型为由节点和边确定的离散渗流模型,其求解区域为离散的孔隙像素点。故需将达西定律离散化,在微小渗流单元内,流体相对渗流阻力R可表示为
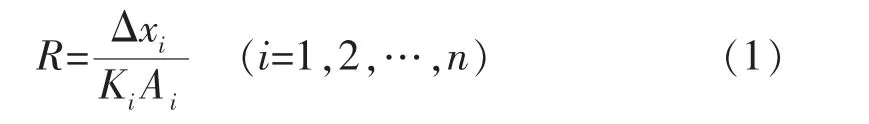
式中:Δxi为孔隙流动路径上的第i-1个孔隙与第i个孔隙的相对空间距离(即边的相对长度);Ki为第i个孔隙的相对渗透率;Ai为第i个孔隙的相对流动面积(二维空间表示相对流动宽度,由最大球算法确定)。
考虑到单宽度的单向单条流动通道的阻力为线性叠加(串联机理),即:
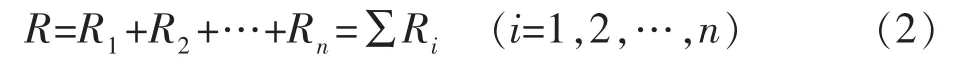
每2个连接节点(即每2个可流动孔隙节点)之间按照串联模式计算流动阻力。注入井到生产井的流动阻力,为流动路径上每2个连通孔隙点之间区域阻力的线性叠加。
流动通道权值实际上是2个顶点和1条边组成的基础单元权值的叠加。对于单元权值来讲,边的长度、渗透率和流动面积A均为顶点属性,计算公式为
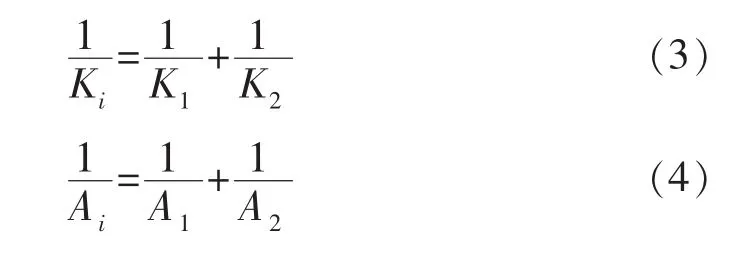
通过上述公式,将节点权值转换到边的权值上。
1.7 邻域修正
在实际的孔隙度分类和路径计算中发现,单纯以某一阈值作为二值化条件的方法存在缺陷,即某些端点孔隙存在可连通性。但是通过绝对的阈值判定可流动孔隙和非流动孔隙,将无法完全判断孔隙连通性,此时通过单法则方法处理的结果就不完全正确。故需要对度(即路径上每一点的直接连接的端点数)为1的端点进行路径完善和补充,利用的算法为膨胀运算。
算法流程为:1)找到细化路径中度为1的端点;2)对每个端点进行以固定半径的圆盘为模板的膨胀运算(或腐蚀运算);3)得到结果与原始图片进行叠加;4)再次进行中轴变换,提取流动路径;5)识别和查找路径,将查找到的路径与原始路径叠合,从而还原端点的连通情况(见图2。图中红线为孔隙的流动路径)。
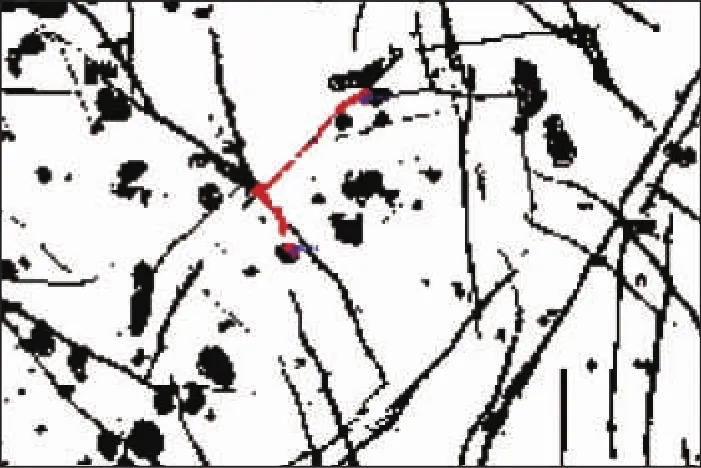
图2 邻域修正与路径通过的端点
从图2可以看到,路径中间存在1个未连通的端点,但是通过算法修正路径之后,端点的两端已连通,红色路径已经被还原。
1.8 查找目标路径
通过生成权值路径之后,采用Dijkstra算法找到地理最短路径和权值最小路径。
2 实例分析
本研究选取塔河油田奥陶系上段的22张连续地震孔隙度切片作为基础数据,通过Petrel软件将图像文件转为灰度坐标数据文件。利用上述方法查找S67,TK687井的连通路径(见图3。图中黑圆点为孔隙,红线首尾端为井位,黑线为裂缝,下同)。黑圆点面积越大,表明孔隙度越大,当孔隙度超过某一界限(根据实际情况设定),可以描述为孔洞或者洞穴。研究中一共查找到4条合理的连通路径,表明两井之间主要通过裂缝连通。

图3 S67井和TK687井的连通路径
图4为S67井和TK687井的井间示踪剂分析结果,即示踪剂突破1 mm裂缝的质量浓度曲线。由图4可以看出,第10次取样后示踪剂质量浓度出现1个峰值,第11次取样后示踪剂质量浓度开始降低,且保持相对稳定。分析结果表明,两井间基本以裂缝连通为主,与图3分析结果一致。
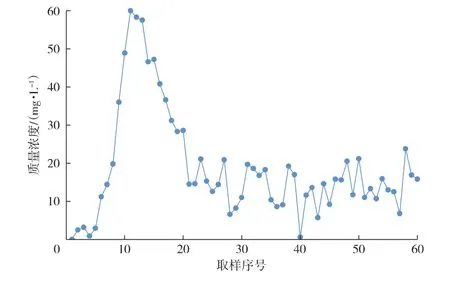
图4 S67井和TK687井井间示踪剂分析结果
该方法也可以识别多对多的大范围井间关系,即多井间的路径识别(见图5。图中红、绿、橙、紫线分别代表井网中与某井匹配的地理最短路径,紫圆点为井位)。例如,图中红线表示与B井连通且地理最短路径的井为D井。实际应用中发现:该方法对裂缝型、缝洞型油藏(即孔隙分布具有典型双峰特征的油藏)应用效果较好;对于非均质油藏,只能识别地理最短路径,难以实现最优路径(即渗流阻力小的路径)识别。
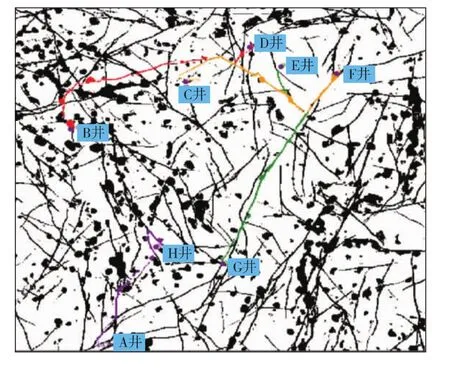
图5 多井间的路径识别
3 结论
1)油藏连通路径识别是分析井间连通结构的基础,是开展注水(气)分析及井网改造的重要依据,对提高油藏采收率具有重要意义。
2)首次将图像处理技术与达西定律相结合,获取流动通道的路径权重,利用迪克斯特拉算法开展连通路径的智能识别,能够克服传统识别方法的诸多不足。
3)智能识别的连通路径与示踪剂分析结果一致,在单井间的识别效果较好,可为同类油藏提供参考。
