超临界CO2压裂起裂压力预测方法
2022-06-09马建民马可欣张富美李小娜杜玉昆赵博赵玉明
马建民 ,马可欣 ,张富美 ,李小娜 ,杜玉昆 ,赵博 ,赵玉明
(1.中国石油大学(华东)石油工业训练中心,山东 青岛 266580;2.中国海洋大学工程训练中心,山东 青岛 266100;3.中国石油青海油田分公司采油一厂,青海 海西 817000;4.中国石油大学(华东)石油工程学院,山东 青岛 266580)
0 引言
我国非常规油气资源具有储层致密、地质结构复杂、黏土矿物含量高等特点,增加了非常规油气田的开发难度。实践表明,大规模水力压裂是非常规油气田开发中最有效的技术手段之一[1-2]。然而,传统水力压裂存在着耗水量大、储层伤害和返排液污染等问题,制约了储层压裂改造的规模和效果,阻碍了我国非常规油气资源商业化开发的进程[3]。因此,亟需探索一种对环境友好的新型无水压裂技术。
超临界CO2压裂是以超临界CO2作为压裂流体对储层进行压裂改造的新型工艺技术[4-5]。压裂过程中,低温液态CO2以较高压力注入井筒,在沿井筒向下流动的过程中被井周地层加热,到达井底时通常处于超临界状态[6]。 在这种情况下,CO2具有高密度、低黏度、强渗透能力等特征,与水基压裂液相比,更容易诱发次生裂缝,形成复杂缝网[7-8],使其在非常规油气储层的压裂增产作业中具有广阔的应用前景。此外,超临界CO2压裂在降低原油黏度、与甲烷竞争吸附、抑制黏土膨胀、节约水资源以及实现温室气体的有效埋存等方面具有优势[9],是一种绿色高效的压裂技术。
储层起裂机理是研究超临界CO2压裂基础理论的起点和重点。对于储层起裂机理的研究可以追溯到20世纪50年代,目前,主要以Hubbert-Willis模型和Haimson-Fairhurst模型为基础。 Hubbert等[10]于 1957年,基于三轴压缩实验提出了受井筒压力影响的近井地带应力模型(Hubbert-Willis模型),并给出井壁破裂模式的判据,但并未考虑径向渗流的影响。1967年,Haimson等[11-12]将渗流项引入井壁应力模型,推导了起裂压力和裂缝缝宽的计算公式。黄荣樽[13]进一步提出了垂直裂缝和水平裂缝起裂、扩展的判据,并认为岩性、交界面、压裂液等均可影响裂缝的起裂和扩展。2000年,Hossain等[14]利用坐标变换和叠加原理建立了射孔井水力压裂的起裂准则。随后,国内外学者逐步开展了井斜和方位[15]、完井和射孔情况[16-17]、地层构造和层理结构[18-19]、储层各向异性以及天然裂缝分布[20-21]等对起裂压力和方位的影响。然而,超临界CO2作为压裂液时,其高渗透性及与岩石相互作用将显著影响井周应力状态,进而改变起裂压力。室内实验研究证实,超临界CO2压裂比常规水力压裂具有更低的起裂压力和更复杂的裂缝网络体系[7,22-23]。 陈立强等[24]考虑超临界 CO2黏度、流体可压缩性及增压速率等因素,建立了超临界CO2压裂起裂压力预测模型,并进行了参数敏感性分析。仲冠宇等[25]建立了考虑井筒温压场和井周应力场的热流固耦合模型,并分析了页岩储层超临界CO2压裂及破裂时间随排量、初始注入压力、注入温度等因素的变化规律。Xiao等[26]将井筒流动方程、井筒增压速率与起裂压力方程耦合,提出了考虑真实井底温压条件的CO2压裂起裂模型,并给出了最优注入排量范围。
综上所述,对于超临界CO2压裂起裂机理的研究目前仍以室内实验为主,尚未形成考虑CO2侵入影响的储层起裂理论体系。针对现有理论模型的不足,本文建立了热流固耦合的超临界CO2压裂起裂压力模型,综合考虑超临界CO2对近井地层温度、孔隙压力以及岩石切向应力的影响,分析了井壁及近井地层的应力薄弱点,进而计算起裂压力,以期为现场施工提供理论指导。
1 理论模型
建立模型的基本假设为:1)不考虑地层水的影响;2)孔隙度和渗透率均为常数且各向同性;3)忽略纵向热量传递;4)岩石满足胡克线弹性定律。
1.1 井周切向应力模型
压裂过程中,裂缝的产生与拉伸破坏有关。取压应力为正,地层产生压裂裂缝的条件为

式中:σθ为有效切向应力,MPa;σt为储层岩石的抗拉强度,MPa;下标θ表示井周角。
CO2渗透性强,到达井底后侵入地层,改变井周孔隙压力的同时对岩石物性造成影响,从而改变井周切向应力;同时,流体与储层之间的温度差异也会引起井周切向应力的改变。
通过上述分析可知,超临界CO2压裂过程中,井周切向应力主要由外部径向应力、井内压力、孔隙压力、热效应等4种基本载荷所引起。根据叠加原理[24],井周有效切向应力的表达式为
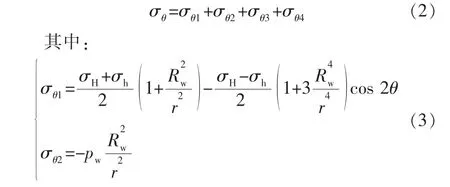
式中:σθ1为外部径向应力引起的切向应力,MPa;σθ2为井内压力引起的切向应力,MPa;σθ3为孔隙压力引起的切向应力,MPa;σθ4为热效应引起的切向应力,MPa;σH,σh分别为最大、最小水平主应力,MPa;pw为井底压力,MPa;Rw为井眼半径,m;r为水平方向上距井眼的距离,m。
CO2几乎不具备造壁性[27],无法在井壁内侧形成泥饼;同时,由于注入过程中井底压力升高以及超临界CO2较强的渗透性,部分流体侵入地层造成孔隙压力升高,从而改变切向应力。定义孔隙压力变化量Δpp为
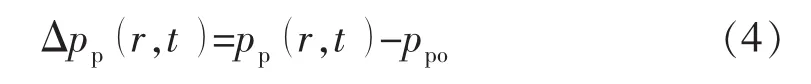
式中:pp(r,t)为井周地层孔隙压力,MPa;ppo为原始地层压力,MPa;t为时间,s。
由孔隙压力变化引起的切向应力分布公式为

式中:η为多孔弹性介质的应力系数;r′为r的积分变量;G,γ为岩石拉梅系数;α为Biot系数;ν为泊松比。
当流体与储层存在温度差时会产生热应力,造成岩石损伤[28-29]。超临界CO2压裂过程中,注入的低温CO2到达井底时与储层存在温度差,由此产生的热应力会影响井周切向应力。定义井周围岩温变场ΔT为

1.2 储层温度和孔隙压力模型
从式(5)和式(7)可以看出,近井地层切向应力与地层温度和孔隙压力有关。因此,建立了力热耦合的储层温度压力模型,分析CO2侵入后裂缝的启动条件。
根据孔隙内流体的质量和能量守恒方程,可得:

式中:φ 为孔隙度;ρf为 CO2密度,kg/m3;Jv为流体流速,m/s;ρs为储层岩石密度,kg/m3;cps为储层岩石的比热容,J/(kg·K);λT为热传导系数,W/(m·K);Qs为热源强度,J/(m3·s);K 为渗透率,μm2;μ 为黏度,mPa·s;p 为孔隙压力,MPa;kT为热渗透系数,m2/(s·K)。
CO2侵入储层后,流体流速受温度、压力影响。流速散度为

2 模型求解和验证
2.1 模型求解方法
由于CO2具有可压缩性,其物性参数对温度、压力的变化较为敏感,同时,CO2的物性参数也会改变近井地带储层温度和孔隙压力分布,进而影响储层局部应力状态。CO2侵入储层后与岩石相互作用,也会影响岩石的物理力学性质[31-32]。因此,在计算起裂压力时,需综合考虑CO2对岩石物理力学性质的影响、流体的渗流与传热以及CO2物性变化等多方面因素,以进行耦合求解,计算流程如图1所示。本文分别采用国际公认的较高精度的 Span-Wagner[33]和 Vesovic 方程[34-35],来计算CO2热物理性质(密度、比热容等)和迁移性质(黏度、热导率等),以保证模型的准确性。
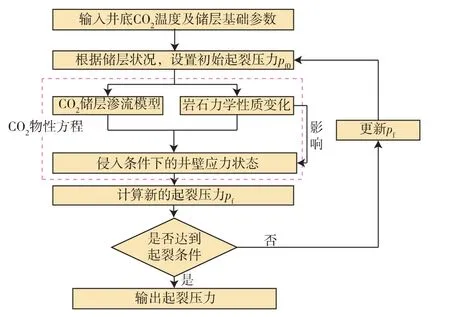
图1 超临界CO2压裂起裂压力耦合计算流程
2.2 模型验证
本文应用某致密砂岩气井超临界CO2压裂施工数据(见表1)来验证模型。现场数据表明,起裂发生在注入初期,起裂压力为48.62 MPa,井底温度为368.97 K,原始地层温度为382.15 K。本文模型计算的起裂压力为48.94 MPa,绝对误差为0.32 MPa,在1%以内,说明本文模型具有较高的计算精度。
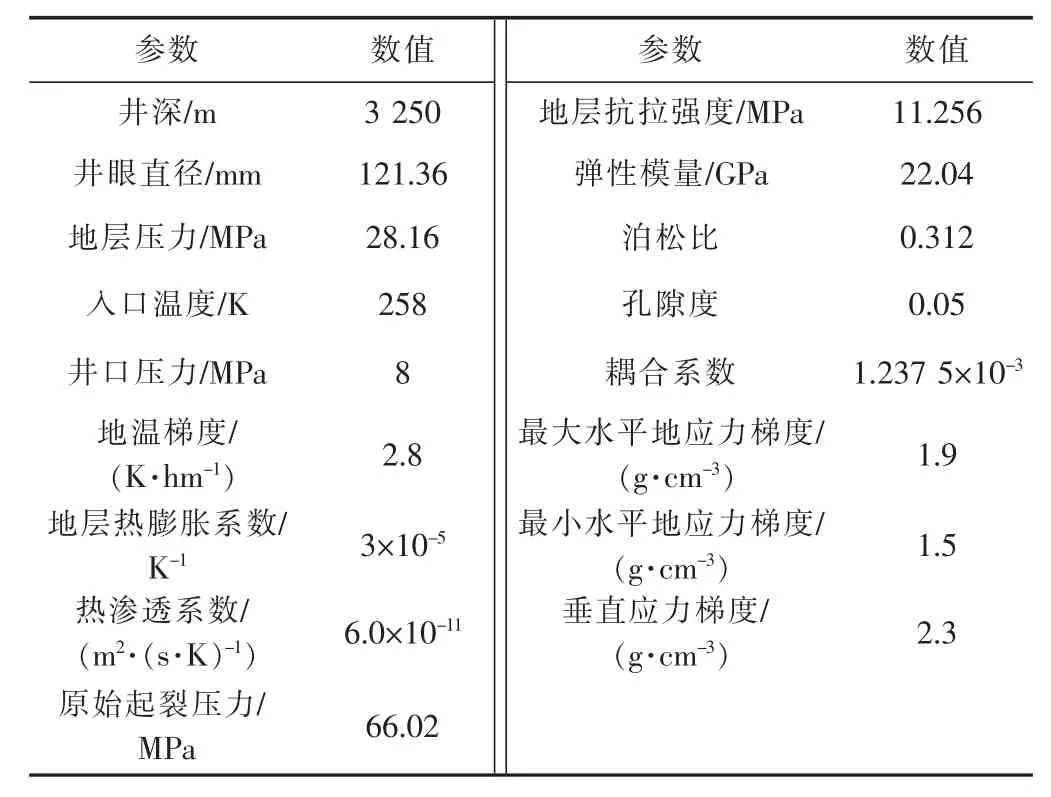
表1 基本参数
3 结果分析
3.1 地层温度和孔隙压力分布
超临界CO2压裂的注入过程中,井底温度逐渐降低且低于地层温度,而井底压力高于孔隙压力,故CO2易侵入地层,影响近井地层温度和孔隙压力[36-37]。前期研究结果表明,排量是影响井筒内CO2温度、压力的主控因素[36],随着排量的增大,井底温度降低。本文采用参考文献[25]的井底温度和压力开展计算,分析了0.5,2.0 m3/min排量下近井地层温度和孔隙压力随时间和径向距离的分布规律(见图2、图3)。
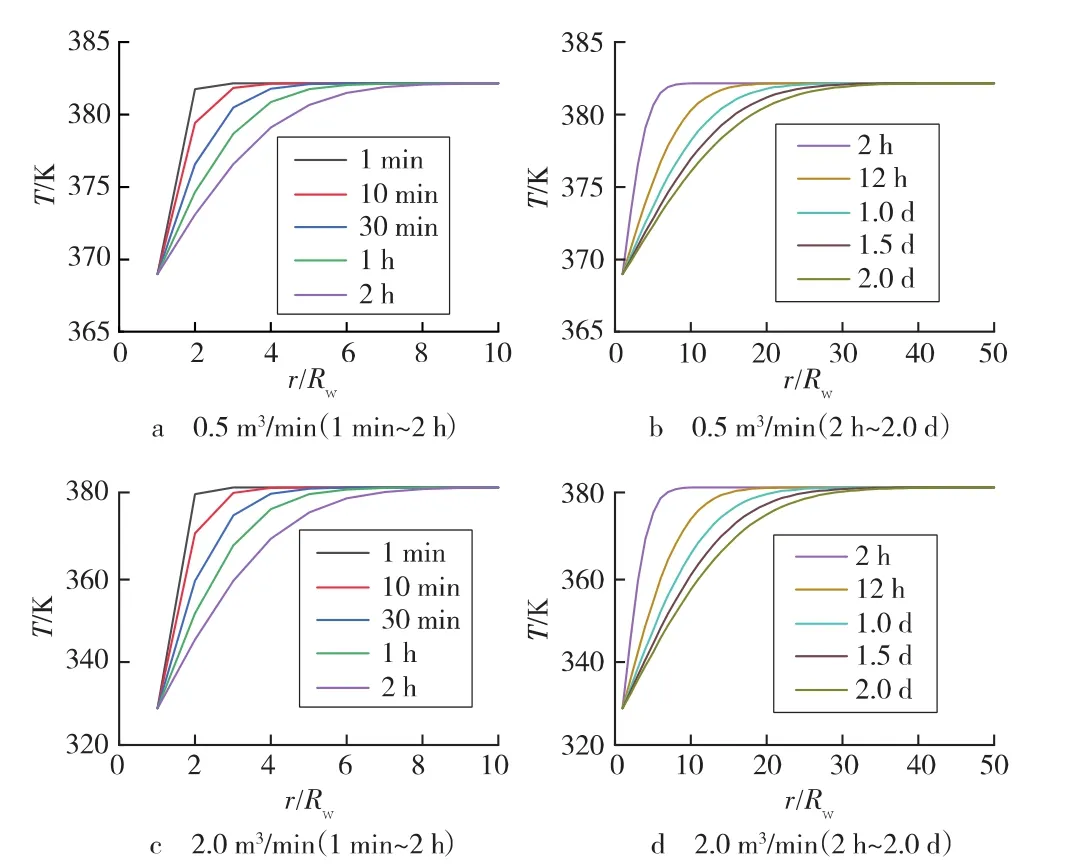
图2 不同排量下近井地层温度分布
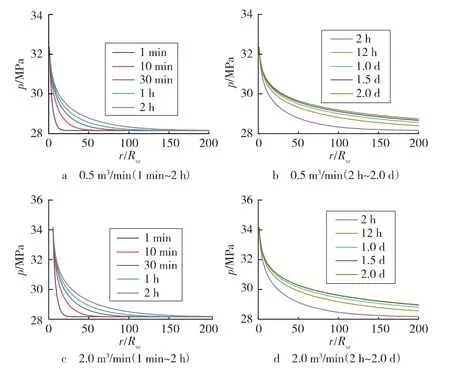
图3 不同排量下近井地层孔隙压力分布
由图2可以看出,当排量从0.5 m3/min增大到2.0 m3/min时,井底温度从368.97 K降低到328.83 K,降低了40.14 K。在不同排量下,随着时间的增加,井底附近地层存在明显的降温,且影响范围逐渐扩大。此外,排量对地层降温波及范围的影响不大。由图3可以看出,相同井口压力下,当排量从0.5 m3/min增大到2.0 m3/min时,井底压力从32.35 MPa升高到34.17 MPa,升高了1.82 MPa。这是由于,重力水头增大引起的压力增量大于排量增大引起的摩阻压降增量。不同排量下,随着时间的增加,井底附近地层孔隙压力升高,且影响范围增大。此外,对比图2和图3可以发现,井底压力的波及速度明显高于井底温度。
3.2 地应力分布
将近井地层温度和孔隙压力代入式(5)和式(7),得到0.5 m3/min排量下由地层温度和孔隙压力引起的岩石应力(见图4)。

图4 地层温度和孔隙压力引起的岩石应力变化
由图4a可以看出,井壁附近热应力(σθ4)为负值,可以有效降低井壁处的切向应力,从而降低起裂压力。热应力最大值在井壁处,为 5.24 MPa,随着径向距离的增大,热应力绝对值逐渐减小并转变为正值。随着时间的增加,热应力负值范围增加。
从图4b中可以看出,井壁附近孔隙压力引起的切向应力(σθ3)为正值,说明孔隙压力升高可引起切向应力的增加,使起裂压力升高。σθ3最大值也出现在井壁处,为0.92 MPa。在CO2压裂过程中,孔隙压力变化对井壁处切向应力的影响小于储层温度。随着径向距离的增大,σθ3逐渐减小并转变为负值;随着时间的增加,σθ3正值的范围逐渐增加。此外,观察图4b可以发现,孔隙压力引起的切向应力集中区域集中在井壁附近。综合来看,超临界CO2压裂时地层温度变化引起的应力大于孔隙压力变化引起的应力。这是由于注入的低温CO2到达井底时,虽然可以达到超临界状态,但温度低于储层温度,从而引起较大的热应力。
图5为0.5 m3/min排量下近井地层切向应力分布。由图可以看出,井壁处的切向应力最小,为41.16 MPa,随着径向距离的增大,切向应力先增大后减小,并逐步趋于稳定,在2~4倍井径范围内存在应力集中区。随着时间的增加,该应力集中区逐渐释放,这是近井地层温度和孔隙压力变化综合作用的结果。
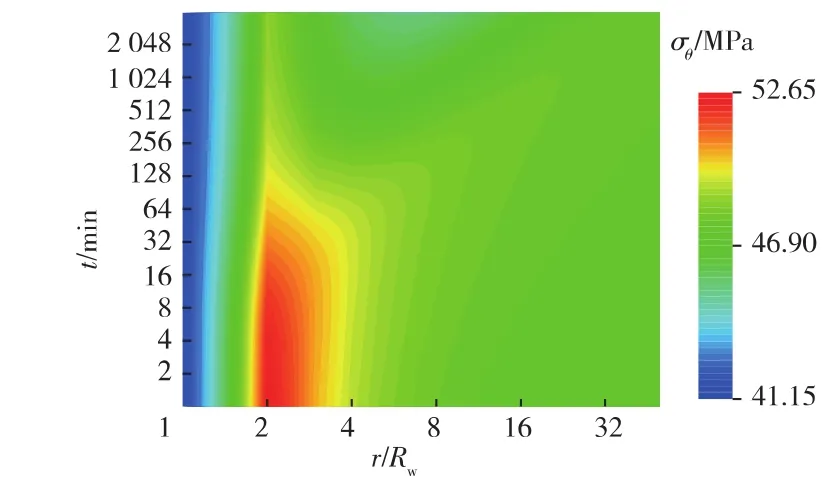
图5 地层切向应力分布
3.3 起裂压力影响因素
由式(9)可以看出,影响超临界CO2压裂起裂压力的因素很多。本文考察了岩石力学性质(泊松比、弹性模量)和井底温度等参数的影响。
3.3.1 泊松比
CO2侵入后,储层岩石轴向应变增大,导致泊松比减小。Ding等[30]对页岩岩心的实验表明,CO2浸泡后,岩心的泊松比从0.280降到0.257,降低了8.2%。
由式(5)、式(7)可以看出,η 和 σθ4均受泊松比影响,前者随泊松比的增大而减小,而后者随泊松比的增大而增大。图6为不同Biot系数下多孔弹性介质应力系数和起裂压力随泊松比的变化情况。由图6可以看出,Biot系数增大,η和pf整体增大。在不同Biot系数下,随着岩石泊松比的增大,η和pf均减小。结合Ding等[30]的研究结果,CO2侵入后岩石的泊松比减小,因而CO2进入地层后可能使得储层起裂压力升高。
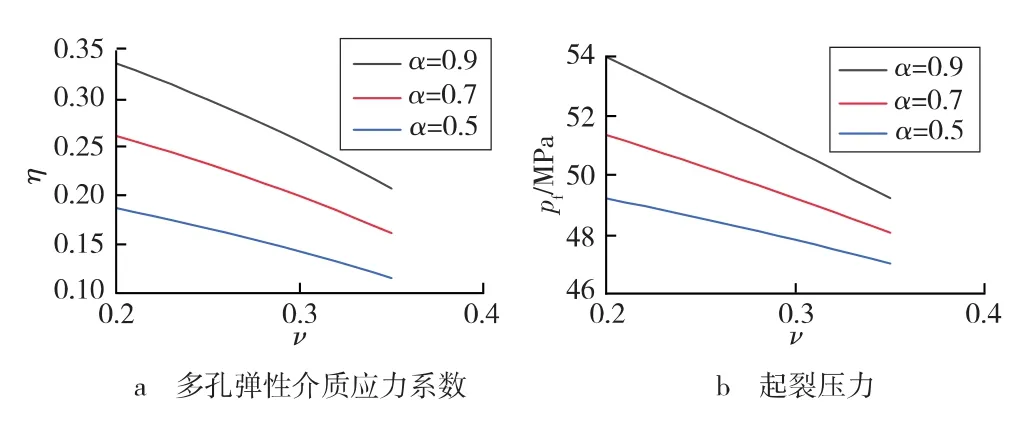
图6 多孔弹性介质应力系数和起裂压力随泊松比的变化
3.3.2 弹性模量
Ding 等[30]研究发现,CO2侵入后,岩心能承受的应变差减小,弹性模量增大。根据式(9)可知,在井底流体温度较低的情况下,随着弹性模量的增大,起裂压力降低。图7为起裂压力随弹性模量的变化情况。由图可以看出,起裂压力随弹性模量增大,线性降低。
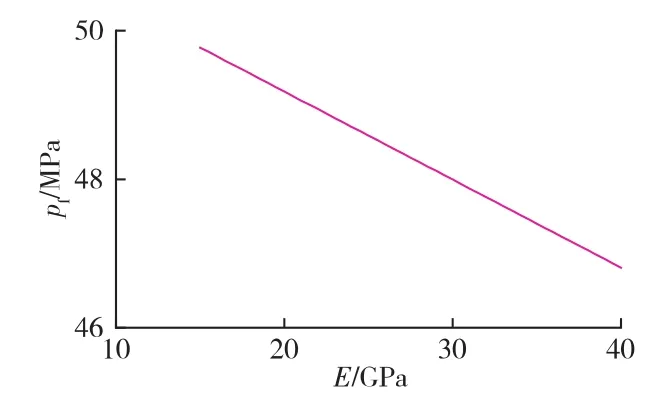
图7 起裂压力随弹性模量的变化
3.3.3 井底温度
井底温度是超临界CO2压裂储层时起裂压力的重要影响因素。不同温差下起裂压力随泊松比的变化情况如图8所示。图中,排量0.5,2.0m3/min对应的地层温度差分别为13.18K(井底温度368.97K)和53.32K(井底温度为328.83K)。
由图8可以看出:不同温差下,储层起裂压力随泊松比的增大,线性递减;随着井底与储层之间温差的增大,储层压力降低,起裂压力随泊松比增大而递减的斜率略有升高。

图8 流体与地层的温差对起裂压力的影响
通过上述分析认为,与CO2接触后储层岩石的泊松比和弹性模量均产生较明显的变化。为了综合分析岩石泊松比和弹性模量变化对起裂压力的影响,给出了井底温度为368.97 K时起裂压力随泊松比和弹性模量的变化(见图9)。
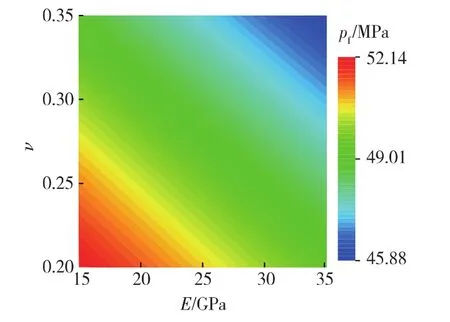
图9 泊松比和弹性模量对起裂压力的影响
由图9可知,泊松比和弹性模量的增大均可引起储层起裂压力的降低。实际应用中,可根据CO2侵入后泊松比和弹性模量的增量来判断起裂压力变化情况。
4 应用实例
基于上述分析,分别计算了排量为0.5,2.0 m3/min时的起裂压力(见表2)。由表2可以看出,超临界CO2压裂可有效降低储层起裂压力。随着排量的增大,储层起裂压力降低,当排量从0.5 m3/min增大到2.0 m3/min,起裂压力从48.94 MPa降低到40.99 MPa,降低了近8 MPa。需要说明的是,虽然增大排量可以降低起裂压力,但同时也带来较大的能量损耗,在起裂阶段,不宜过度追求高排量下的低起裂压力。
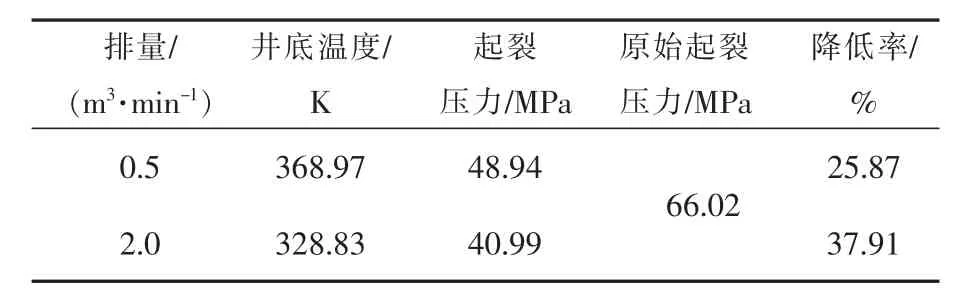
表2 不同排量计算结果对比
从动态压裂过程看,低起裂压力有助于裂缝的产生,裂缝产生后会在井底压力下迅速扩展。由于温度场的传播速度较慢,故其产生的热应力可以诱导次生裂缝的产生和扩展,进而在储层内产生具有较高导流能力的裂缝网络体系。
5 结论
1)超临界CO2压裂可有效降低储层起裂压力,随着排量增大,储层起裂压力降低。
2)随着CO2的注入,井底温度、压力对近井地层的影响沿径向扩大,井底压力的波及速度高于井底温度。排量主要影响近井地层温度和孔隙压力的大小,对波及速度影响不大。
3)地层温度和孔隙压力引起的切向应力最大值均位于井壁处,前者减小井壁处的切向应力,后者增大井壁处的切向应力,地层温度变化引起的应力大于孔隙压力变化引起的应力。整体来看,切向应力最小值也位于井壁处。
4)泊松比增大、弹性模量增大、井底温度降低均可使储层起裂压力降低。
