螺旋压缩弹簧的加速贮存行为研究

赵 薇 ， 宫晓春 ， 洪 洁 ， 王 强

（北京强度环境研究所，北京 100076）

0 引言

固体导弹参加贮存延寿的弹体结构主要包括铆钉、起吊接头、起吊组件、发动机裙结构模拟件、尾翼接头、尾翼、惯组基座、惯组基座试片、尾段、止脱弹簧等产品。导弹结构产品中的连接件与弹性元件是贮存过程中的薄弱环节，弹性元件如弹簧、金属减震器、波纹管等，是影响导弹结构可靠性的重要因素之一，也是贮存环节中的薄弱点[1-2]。如尾翼弹簧若经长期贮存，发生应力松弛导致其贮存的能量减小至一定值后，在导弹使用过程中将不能使尾翼展开至规定位置，导致导弹飞行姿态和飞行轨迹不符合要求而发生失效。

应力松弛是材料在服役时出现的一种物理现象，指在恒应力的作用下，产品的总变形量恒定时，内部弹性应变随着时间逐渐转化为塑性应变的行为[3]。材料发生应力松弛后，其内部贮存的弹性能减小，造成能量不足，影响产品的使用。因此，产品的抗松弛性能对其设计和使用具有重要意义。

弹簧失效的模式并非单一，其中应力松弛是最主要的失效模式之一[4]。虽然早在1868年J.C.Maxwell对应力松弛规律及其影响因素进行了相关研究[5]，然而迄今人们对应力松弛机制、发生条件与抗应力松弛设计等尚未建立起统一的理论，且无通用的应力松弛测试方法。另一方面，对于元件的寿命预测，虽然曾有研究者总结出了数种方法[6-8]，但所涉及的物理机制模糊。因此，研究应力松弛随外界因素的变化规律与松弛机理，对于提高元件的抗应力松弛性能，准确预测弹簧件使用或贮存寿命，具有重要的理论和实际意义。

在室温工作条件下弹簧的松弛速率较低，相对于较高温度下的应力松弛试验，室温下的应力松弛试验耗时较长，有时长达105h以上，而且结果对很多参数十分敏感。因此，本研究随机抽取同一热处理工艺后的T9A螺旋压缩弹簧，对其进行较高温度下的短周期加速应力松弛试验获得其松弛特性，通过观察分析松弛行为，探究其应力松弛机制，在此基础上建立松弛寿命方程，并对弹簧在室温工作条件下的长周期贮存寿命进行合理预测。

1 应力松弛试验

参加试验的是应用于尾翼的螺旋压缩弹簧，弹簧材料为T9A，材料成分见表1。根据材料成分计算材料平衡相图见图1[9]。由图可见，材料在室温下，其主要存在相为体心立方的A2结构。这种主要存在相的转变温度高于500 ℃。因此，确定预试验温度范围为室温至300 ℃。

图1 T9A弹簧材料平衡相图Fig.1 Balance phase diagram of T9A

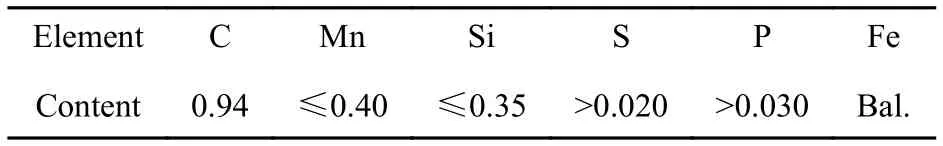
表1 T9A弹簧丝材料成分表（质量分数 /%）Table 1 Chemical composition of T9A spring wire (mass fraction /%)

经摸底试验后，发现温度大于140 ℃时，弹簧的应力松弛曲线相较于较低温度下的应力松弛曲线出现了明显的区别。故确定正式试验温度为80、100、120、140 ℃。

在配备闭环控制系统的电子试验机上进行弹簧的应力松弛试验。三段式电阻炉提供等温环境。试验中3个热电偶实时监测弹簧的上、中、下3部位，保证温度波动不超过±1 ℃。在试验温度下，采用弹簧贮存时的实际应力126 N为初始应力，压缩量为60 mm，在预定的压缩量下保持24 h，采样频率为 60 次/min。

将弹簧置于电子式万能材料试验机上进行应力松弛试验，松弛曲线见图2。

图2 螺旋压缩弹簧应力松弛曲线（P0=130 N）Fig.2 Stress relaxation curve of spiral compression spring (P0=130 N)

2 应力松弛行为分析

分析可以发现，尽管弹簧结构与标准应力松弛试验的试样不同，但其应力松弛行为相似。

观察弹簧的载荷−时间曲线可以看到，弹簧的应力松弛均分为2个阶段：第一阶段，弹簧的载荷随着时间快速下降，下降幅度很大，但持续的时间较短（约100 s），随着时间的增加载荷下降的速率变缓，逐渐进入第二阶段；第二阶段，弹簧的载荷随着时间的增加出现缓慢下降的趋势，且载荷下降的速率不随时间的继续增加而出现明显的变化，曲线呈线性，该阶段持续的时间较长，但载荷下降的比率要远低于第一阶段。随着时间的继续增加，弹簧的载荷值逐渐趋于稳定，无明显的下降趋势。

对比不同温度下弹簧的载荷−时间曲线可知，4个温度下弹簧的载荷−时间曲线相似，说明4个温度下弹簧的松弛对应的微观机理均未发生变化。进一步分析发现，不同温度对弹簧应力松弛行为的影响有很大差异。温度越高，弹簧在第一阶段时载荷下降的越多，进入第二阶段的时间越早。弹簧在140 ℃时，第一阶段发生的载荷损失约为80 ℃第一阶段发生的载荷损失的6倍，但其所用的时间仅为80 ℃第一阶段时间的1/5。随着温度升高，弹簧在第二阶段载荷下降的也越明显。

3 应力松弛方程拟合

材料的应力松弛第二阶段通常可用经验公式（1）拟合，其中：a为松弛开始时的初应力，即第二阶段直线方程在纵坐标轴的截距；b为应力松弛率vs，即第二阶段直线方程的斜率。

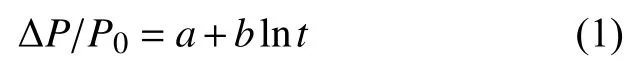
其中，ΔP=P0−Pt为应力松弛中的载荷损失量，a、b为与温度相关的常数。

当材料的应力松弛是由位错的热激活过程控制时，通常认为松弛率vs与温度T及位错越过障碍所需的激活能Q之间满足Arrhenius公式：

其中，vs可以定义为：

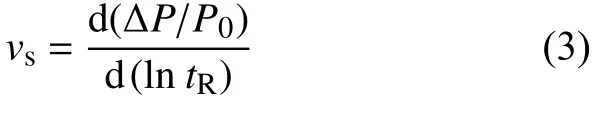
式中：γ为特定常数；T为热力学温度，K；k为玻尔兹曼常数（k=8.6×105eV/K），tR为松弛时间，P0为初载荷。对式（3）两边取对数可得：

令t=1，带入式（1）中可得：

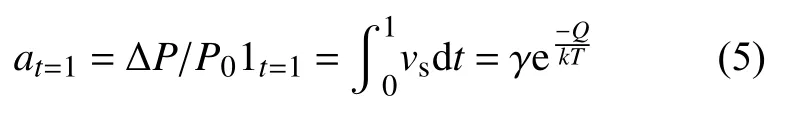
式（5）两边取对数可得：

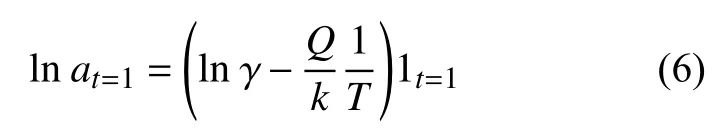
由此可建立基于Arrhenius模型的应力松弛方程。

利用方程（1）对应力松弛的第二阶段进行线性拟合，可得a、b值及拟合精度，见表2。不同温度的载荷损失率曲线如图3所示，各温度下的载荷损失率拟合曲线见图4。

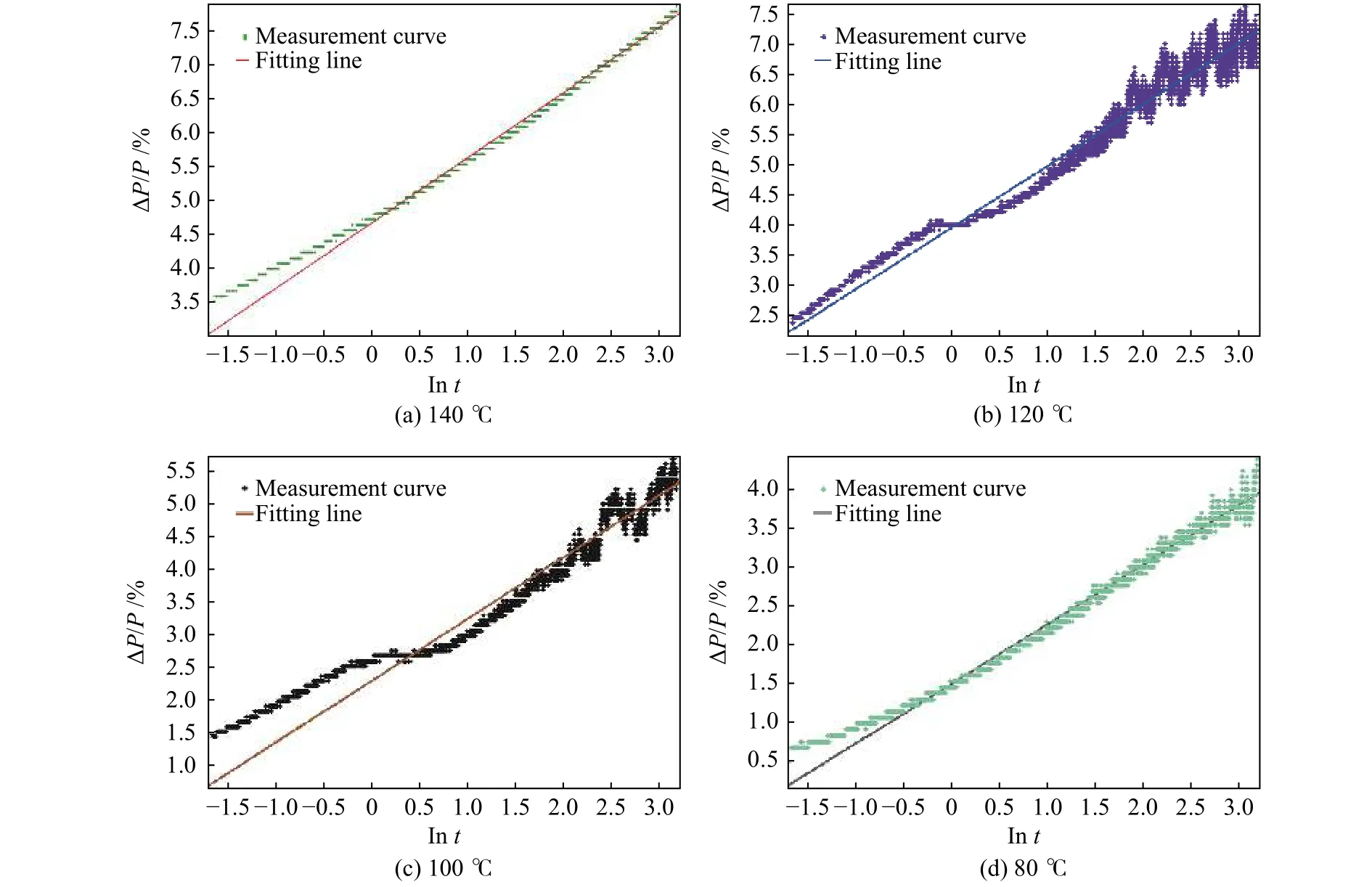
图4 各温度下的载荷损失率曲线拟合图Fig.4 Curve fitting of load loss rate at different temperatures

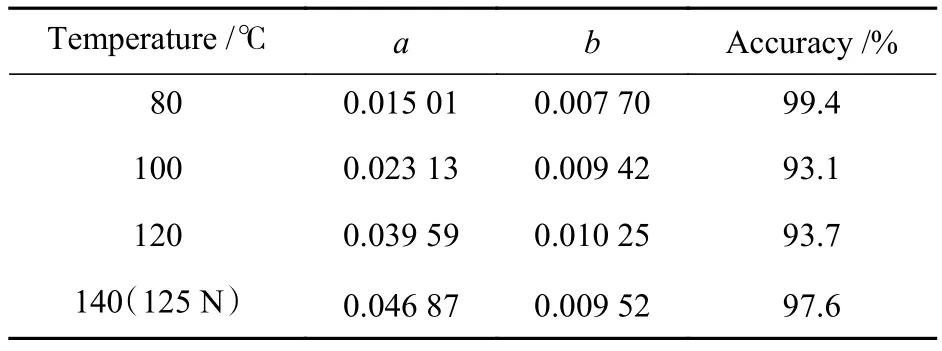
表2 Arrhenius方程拟合参数值及拟合精度Table 2 Fitting parameter value and fitting accuracy of Arrhenius equation

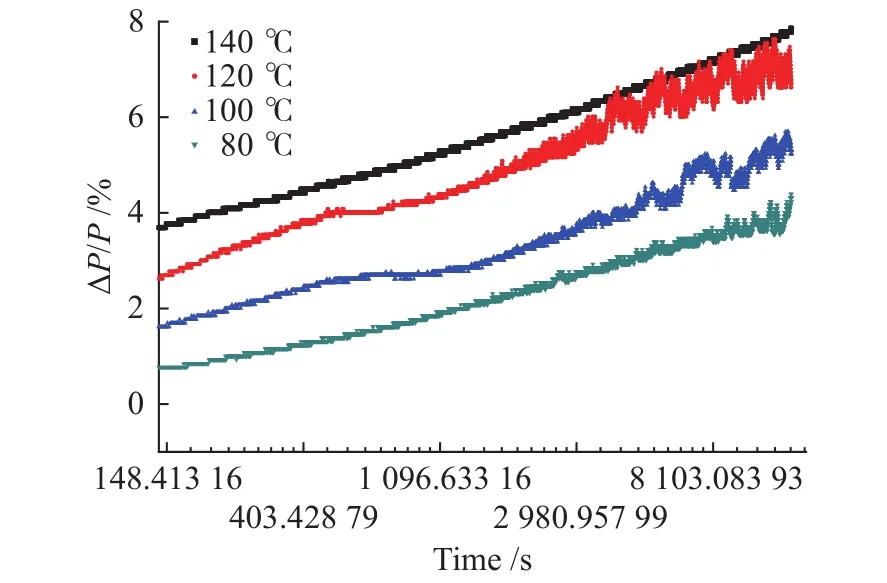
图3 不同温度的载荷损失率曲线Fig.3 Load loss rate curves at different temperature

利用式（4）对松弛率vs进行拟合，利用式（6）对a值进行拟合。拟合结果如式（7）、式（8）所示：

由以上分析计算结果可知，在松弛的第二阶段，当T=80 ℃时，1 h后应力松弛率变化不大；但当T=140 ℃时，在相同初始应力条件下，1 h后载荷损失率显著提高。表明在应力松弛初期，温度为应力松弛的主要影响因素。松弛过程中环境温度决定了位错等缺陷的能量大小，主导着位错的增殖、湮灭过程[10-14]。低温时，在应力松弛初期，弹性变形导致弹簧微观存在较大的应力水平，使弹簧位错增殖速率高于位错湮灭速率，弹簧内部可动位错密度较高，松弛主要取决于饱和的位错增值速率。而随温度升高，弹簧位错增殖速率开始低于位错湮灭速率，松弛主要取决于位错的湮灭速率，此时温度成为影响应力松弛的主导因素[15-16]。

从不同温度、相同应力松弛水平（Δσ/σ0=1%）时弹簧贮存寿命预测的拟合结果可以发现，在进入应力松弛第二阶段后，弹簧应力松弛的速率（载荷损失率的斜率b）随着温度的升高而升高。当T=80 ℃时，松弛的速率为 0.007 70，当T=140 ℃时，松弛的速率为0.009 52。但将T=140 ℃的数据与T=120 ℃的数据对比发现，2个温度条件下的应力松弛的速率差别很小，说明该种弹簧第二阶段的应力松弛的速率对温度变化的敏感程度较低。这与T9A弹簧钢材料的热稳定性相符[17-18]。

根据式（7）、式（8）可以得出弹簧在室温下，第二阶段载荷损失率的方程为：

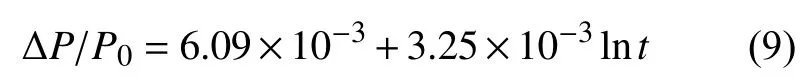
如果计算弹簧贮存20 a后是否符合要求，将t=20×365×24×3600 s带入式（9），即可计算出其载荷损失率为7.2%。按载荷损失率小于12%的要求，可得出弹簧满足贮存寿命20 a要求的结论。

4 结论

1）应力松弛是导致螺旋压缩弹簧发生失效的主要原因，松弛速率随着温度升高而加快，故螺旋压缩弹簧的加速贮存试验可通过升温加速其应力松弛过程进行。

2）弹簧的应力松弛分为2个阶段：第一阶段弹簧的载荷值下降较快，载荷损失率较大，但该阶段持续时间很短；第二阶段弹簧的松弛趋于稳定，载荷值变化较小，弹簧进入长时稳定阶段，可通过对该阶段进行评估获得弹簧的应力松弛规律。

3）基于应力松弛过程的热激活特性，构建T9A螺旋压缩弹簧的应力松弛动力学方程，并对其室温下的贮存寿命进行合理预测。预测结果表明，T9A螺旋压缩弹簧满足常温25 ℃，载荷损失率小于12%、贮存20 a的要求。