钢丝绳声发射信号传播特性分析

张鑫鹏， 黄丽霞， 沈佳卉， 尉桂芝， 朱 萍，王海涛， 胡 强， 李秋锋,*

（1.无损检测技术教育部重点实验室（南昌航空大学），南昌 330063；2.中国电建集团江西省电力设计院有限公司，南昌 330096；3.中国航发沈阳黎明航空发动机有限责任公司，沈阳 110043；4.中建一局集团第二建筑有限公司，北京 100161）

0 引言

钢丝绳是将若干直线钢丝经过螺旋缠绕后形成的螺旋结构绳索，具有较高的抗拉强度、抗疲劳强度和冲击韧性。同时，由于钢丝绳柔韧性较好、自身质量轻及安全系数大等特点，使这一构件成为承受拉伸载荷、交变载荷等多种载荷的理想工程部件[1]。然而，由于钢丝绳工作环境复杂，特别是在承受较大载荷时容易产生断丝、磨损等缺陷，严重影响其使用寿命及安全，为确保钢丝绳在使用过程中的安全性，针对钢丝绳的无损检测技术是如今实际工程应用中的热点问题。目前，针对钢丝绳无损检测方法应用较广的是超声检测法、光学检测法、电磁检测法、声−超声检测法和声发射检测法[2]。

声发射（Acoustic Emission，AE）检测是指，通过接收工件受内力或外力作用产生变形或破断时的弹性波信号，来判断该工件性能或结构安全性及完整性的检测方法。钢丝绳在载荷作用下发生塑性形变、生成裂纹及股丝断裂时会产生声发射信号，该信号沿钢丝绳传播经传感器接收并转换为电信号，从而反映钢丝绳损伤信息[3-6]。

近年来，邵永波等[7]研究了钢丝绳的损伤机理、断丝模式及声发射信号特征；聂林等[8]通过经验模式分解和支持向量机提出了一种较为可靠的提取钢丝绳断丝声发射信号特征的方法，可较准确地识别钢丝绳缺陷声发射信号；钱骥、陈鑫等[9-11]采用小波变换从时频能量的角度研究了超声导波在钢丝绳中的传播特性与规律，通过单点波动信号对钢绞线中超声导波的模态成分进行了分析，发现其声波在时频领域的特性可以有效反映结构损伤。

本研究通过设置不同频率、不同位置的钢丝绳声发射源，对其传播过程中所产生的声发射信号的幅值与弹性应变能密度进行提取，同时通过小波变换分析声发射信号的时频信息，并结合理论频散特性，对比分析声发射信号的模态分布，研究其在钢丝绳结构中的传播特性，为实际工程检测提供理论支撑。

1 钢丝绳声发射源的选取及仿真条件

1.1 钢丝绳声发射源的选取

常规钢丝绳断丝声发射信号的频率主要在500 kHz以下，且钢丝断裂的AE源频率约为150 kHz[12-13]。为得到钢丝绳中较为精确的声发射信号传播过程，基于等效体力理论，本研究采用150、500 kHz的正弦信号来模拟断丝声发射源，其激励表达式为：

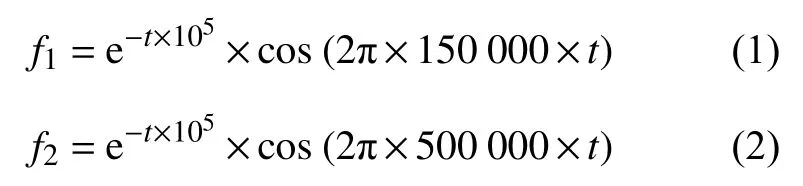
式(1)模拟的是常规断丝声发射源，式(2)模拟的是高频断丝声发射源，通过不同频率的激励信号来横向对比应力波在钢丝绳内部传播的状态。

1.2 仿真条件

为了得到准确的结构中随声发射现象而产生的弹性应力波传播特性，需要设置与模型和激励信号相适应的空间分辨率和时间分辨率。空间分辨率则是划分网格的单元长度，时间分辨率是在仿真中每一时间步的步长[14-16]，公式分别为：

式中：Δt为时间间隔；fmax为结构中声发射信号的最高频率；K为对时间采样和空间采样的比例缩放因子，通常取10~20，本研究中K取10；le为所划分网格的单元长度；lmin为结构中声发射信号的最小波长。

根据所采用的2种不同激励信号频率，由式(4)可得仿真时间步长 Δt为 0.6、0.2 μs。lmin则是根据结构中横纵波波速与fmax所确定，计算公式为：

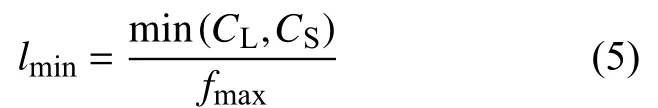
式中：CL、CS分别为纵波、横波波速，其计算公式为：

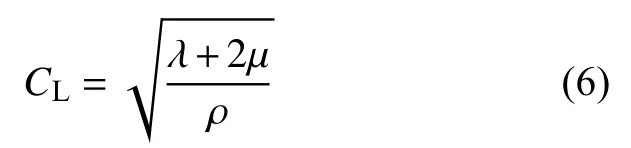
式中，λ、μ为材料拉梅常数，其分别由式(8)、式(9)确定。

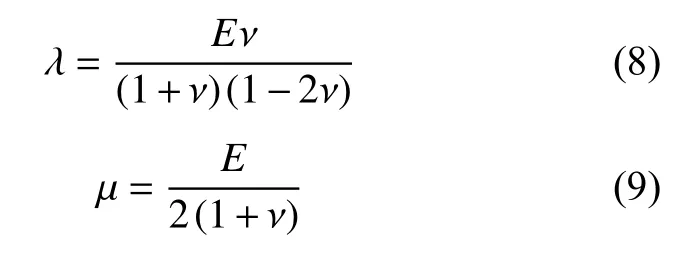
在仿真研究中，需要提前对三维模型定义材料及参数。本研究中单股钢丝绳所选取的材料为316退火不锈钢，经式(8)、式(9)计算得到该材料拉梅常数，再代入式(6)、式(7)得到其对应的横波、纵波波速（表1）。根据参数建立仿真环境，并开展仿真运算。

表1 316 不锈钢材料退火参数Table 1 Parameters of the annealed 316 stainless steel

1.3 导波模态与频散特性

根据边界条件的不同，波在固体介质中的传播分为体波和导波两种形式。在无限大均匀介质中传播的是体波，而在边界受限介质中传播的则是导波。钢丝绳结构中的超声导波由于其波导结构接触复杂，使得导波频散特性的理论求解非常困难。构成钢丝中的导波可视为圆柱体中的导波，通过将单根钢丝的频散特性推广至钢丝绳中，可以对钢丝绳结构的导波模态进行分析[17-20]。

声波在无限长圆杆中传播，有3种振动模式，并对应3种模态，分别是对称纵向模态L(0,n)、对称扭转模态T(0,n)和非对称弯曲模态F(1,n)，其波动方程为：

式中：φ为柱坐标系的体积不变量；t为时间；ωr、ωz、ωθ分别为r、z、θ3个方向的旋转矢量分量；λ、μ为材料的拉梅常数；R为钢丝半径；ρ为材料密度；ur、uz、uθ分别为r、z、θ3 个方向的位移分量。

3种振动模式的边界条件分别是：

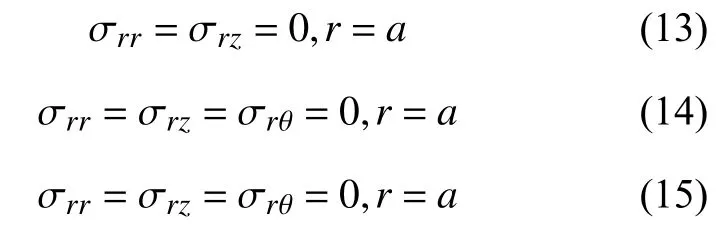
式中，a为圆杆截面半径。

根据式(10)~式(15)，可求得不同模态导波的频率特征方程，由导波群速度与频率的关系可得到不同模态导波的频散曲线，通过波速、传播距离和时间的关系将频散曲线叠加到时频图中，从而得到叠加频散曲线的钢丝绳声发射信号时频图。图1为单股钢丝绳的理论频散曲线。

图1 单股钢丝绳理论频散曲线Fig.1 Theoretical dispersion curve of a single wire rope

2 仿真试验与结果分析

2.1 钢丝绳三维模型的建立

针对钢丝绳仿真研究，首先利用SolidWorks软件对1×7单股钢丝绳进行建模，如图2所示。单股钢丝直径为3 mm，长度为100 mm，公称抗拉强度为1670 N/m2。将模型存储为.stl文件导入Comsol中，对钢丝绳的三维模型施加约束，选择固体力学物理场，根据前述定义材料参数和仿真条件，并设置低反射界面降低端面回波。

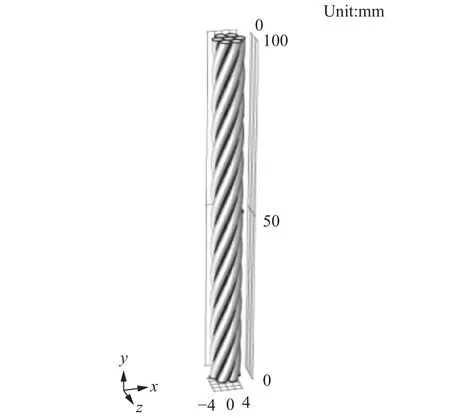
图2 1×7 单股钢丝绳三维模型Fig.2 Three-dimensional model of a single wire rope

在实际应用中，钢丝绳受载荷影响，外层钢丝易产生裂纹发生断裂，而中心丝在载荷较大时也可能会由于颈缩现象产生断裂。根据仿真模型，在钢丝绳的下端面建立2个激励源，即A(0,0,0)、B(4.3,0,0)（单位：mm，下同），其中A点是下端面中心点，用来表征钢丝绳中心股丝的断丝信号；B点是下端面近表面点，用来表征外层股丝的断丝缺陷信号（图3）。

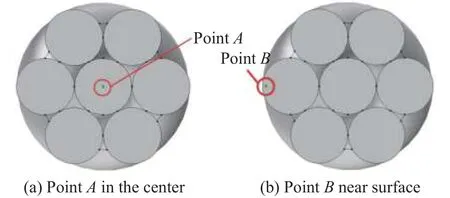
图3 钢丝绳下端面激励点布置Fig.3 Arrangement of excitation points on the lower end of the wire rope

由于实际检测中声发射探头是布置在钢丝绳表面来接收AE源信号的，故仿真中在钢丝绳模型近表面设置C（4.1,78,0）、D（4.3,50,0）、E（4.2,23,0）3个采样点，如图4所示。在A点施加沿轴向y方向的频率分别为150、500 kHz的激励源信号，在B点施加沿径向x方向的频率分别为150、500 kHz的激励源信号，仿真时间步长Δt分别为0.6、0.2 μs，时间总步长为100 μs，进行4组仿真试验。图5为模拟断丝声发射信号的波形图，基于等效体力理论表示声发射源，采用固体力学场中的力源函数，以总力Fp表示。

图4 钢丝绳近表面采样点布置Fig.4 Layout of sampling points near the surface of steel wire rope

图5 声发射源波形图Fig.5 AE source waveform

2.2 仿真测试与结果分析

通过仿真计算结果提取位移云图，可以清晰地看到钢丝绳中声发射源所产生的声波传播路径。如图6所示，位于端面中心y方向激发的声发射源所产生的质点振动多为纵向的对称模式，而位于端面近表面x方向激发的声发射源产生的波动多为径向的非对称模式。

图6 钢丝绳声波传播路径Fig.6 Sound wave propagation path of wire rope

2.2.1 不同类型声发射源传播特性分析

为研究钢丝绳中不同声发射源的传播特性及模态特征，读取结构表面3个采样点的位移及弹性应变能密度的波形图进行分析。

图7、图8为设置在端面中心的频率为150 kHz的声发射源，在3个采样点所产生的位移和弹性应变能密度图。由图中可以看出：声波分别在3个采样点的34、22、10 μs时达到位移幅值最大值，对应的最大幅值分别为0.14、0.16、0.19 nm；随着声波传播距离的增加，幅值均逐渐衰减，其衰减的规律与采样点距波源的距离和波源信号的波速大致相对应。从能量角度来看，3个采样点分别在位移幅值达到最大时，对应的弹性应变能密度同时达到最大，分别为0.075、0.095、0.110 mJ/m3，其能量衰减也符合一般规律。

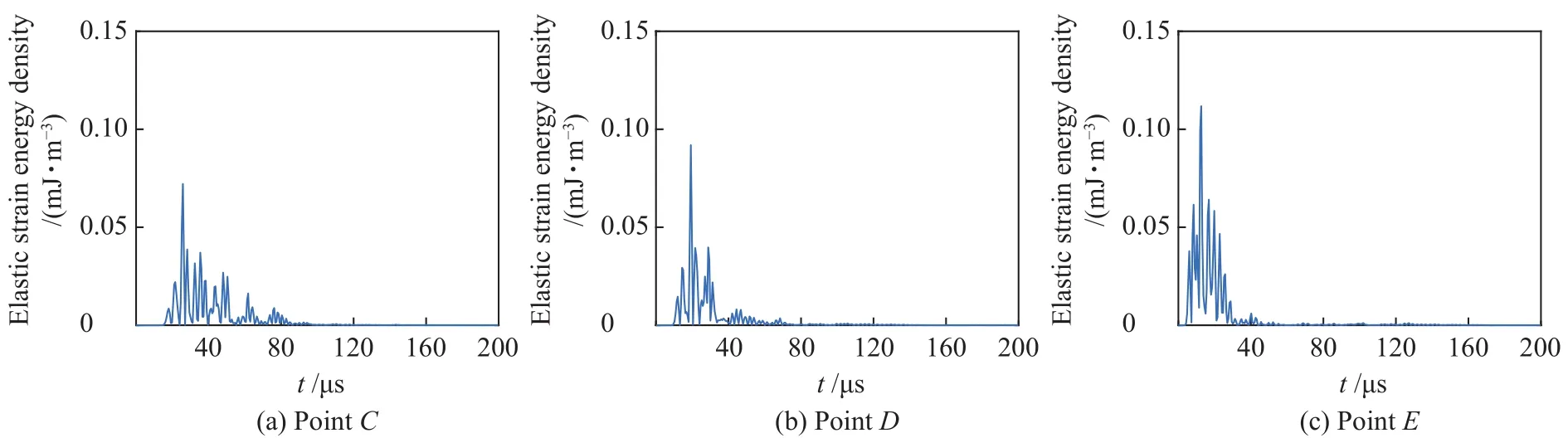
图8 150 kHz 端面中心 AE 源采样点弹性应变能密度图Fig.8 Elastic strain energy density map of sampling points of AE source at the end-face center (Frequency: 150 kHz)

当150 kHz波源设置在端面的近表面时，由于激励方向不同，对应采样点接收到的波形与在端面中心激发所产生的波形图有较大差距。各点位移幅值达到最大的时间分别为 75、25、15 μs，对应的最大幅值分别为 0.10、0.11、0.18 nm。声波在C点达到最大幅值的时间与根据理论波速计算的时间偏差较大，C、D点的最大位移幅值衰减较小，且声波在传播到C点时逐渐产生了第二个位移幅度峰值。各采样点的弹性应变能密度最大值分别为3.75、3.90、0.36 mJ/m3，对应时间为35、25、15 μs，能量在声波传播到D点时有所提高，传播到C点时大幅衰减。

图9、图10为 500 kHz端面中心 AE源在各采样点的位移和弹性应变能密度图，3个采样点的最大位移幅值分别为 0.014、0.016、0.031 nm，对应的到达时间分别为 45、20、10 μs，声波在C点产生的质点振动达到最大的时间较长，且位移幅值从E点到D点的衰减较大，从D点到C点的衰减则较小。各点的能量弹性应变能密度最大值为0.012、0.011、0.073 mJ/m3，能量在声波从E点到D点时衰减很大，在传播到C点时几乎无衰减。各点到达最大值的时间为分别 55、45、25 μs，且C点的弹性应变能密度图在75 μs产生第二个波峰。

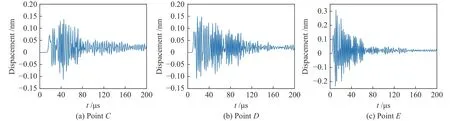
图9 500 kHz 端面中心 AE 源采样点位移图Fig.9 Displacement map of sampling points of AE source at the end-face center (Frequency: 500 kHz)

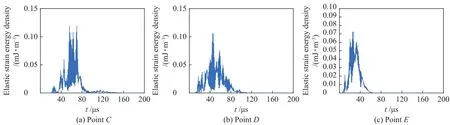
图10 500 kHz 端面中心 AE 源采样点弹性应变能密度图Fig.10 Elastic strain energy density map of smapling points of AE source at the end-face center (Frequency: 500 kHz)

当500 kHz波源设置在端面近表面处时，声波在采样点产生的位移变化较大，从位移−时间图无法看出明显规律。从弹性应变能密度图来看，各点的最大值分别为 0.125、0.560、0.340 mJ/m3，达到最大值时间分别为 50、30、25 μs，能量变化也是先增后减，在中端达到最大，随后在远端大幅衰减。

通过对比以上仿真实验数据发现：150 kHz的声发射源在不同位置激发的弹性波时，位于端面中心的波源依次对各采样点产生的位移和弹性应变能密度最大值衰减较为稳定，且各点达到最大幅值的时间大致与各点距波源的距离除以AE源中心频率对应的波速所得的理论时间值相吻合；位于端面近表面的波源由于激励方向的不同导致结构中存在复杂模态成分，导致C、D点的位移最大幅值较为相似，达到最大值的时间与理论值偏差较大，各点的弹性应变能密度在声波传播过程的后半程衰减很大。

当波源频率为500 kHz时，端面中心激发的声波在各采样点产生的位移最大幅值变化与150 kHz有所差异，由E点到D点的衰减较大，由D点到C点的衰减很小，能量的变化也与位移相似，前半程衰减很大，后半程弹性应变能密度变化很小；端面近表面处激发的声波在各采样点处所产生的速度和能量变化皆为前半程增高，后半程大幅下降，这是由于沿x轴激发的声发射源产生了较多的非对称F模态，在声波传播到后半程时，频散现象加剧，声波在结构中反射折射程度增加，能量大幅减小。

2.2.2 不同类型声发射源的模态分析

由于受钢丝绳结构限制，声波在介质中传播时，在结构边界处产生大量反射、折射等，会以导波的形式传播。为了分析在钢丝绳中的模态特性，取3个采样点的数据，对所得信号通过小波变换进行时频分析，选取时频窗较小的Morlet小波作为母小波，分别设置小波中心频率为150、500 kHz，通过尺度变换和时移后得到不同区间的基小波，再分别和对应基小波的区间的原始信号乘积再积分，产生的极值对应的频率就是原始信号这一区间含有的频率，并将理论频散曲线叠加到时频图中观察分析不同中心频率导波的模态与传导距离的关系[21]。

图11为150 kHz端面中心y方向波源在3个采样点产生的时频图。图中曲线为不同模态的频散曲线，由于信号中心频率较低，其产生的导波能量主要集中在低阶模态。3个采样点的最高幅值区集中在 150 kHz 左右 (120~180 kHz)，这与波源信号中心频率(150 kHz)相符合。通过分析其高幅值区域上所覆盖的模态频散曲线可以看出主要成分为L(0,1)，而T(0,1)与F(1,1)混杂在一起无法分辨。由于激励信号产生的主要为轴向和周向振动，在 300 kHz左右 (270~370 kHz)产生了幅值较低的T(0,1)、F(1,3)和L(0,1)，随着声波传导距离的增加，T(0,1)、F(1,3)和L(0,1)的幅值相较E点明显下降。

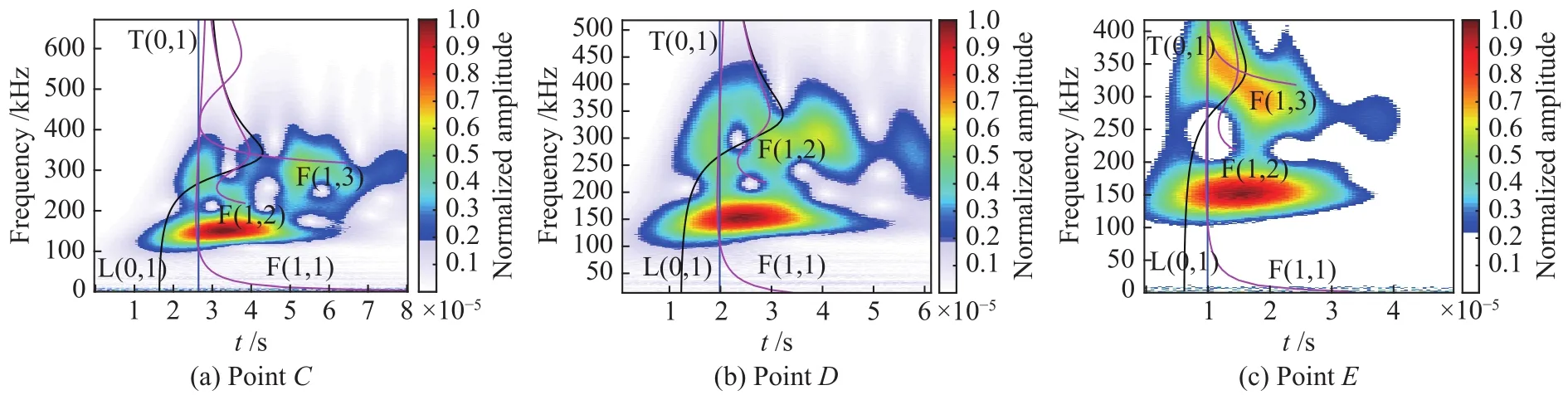
图11 150 kHz 端面中心 AE 源信号时频与频散曲线叠加图Fig.11 Overlay of time-frequency and dispersion curves of AE source signal at the end-face center (Frequency: 150 kHz)

图12为150 kHz端面近表面处x方向波源在3个采样点所产生的时频图。可以看出，声波在传导初期(E点)的高幅值区主要为130~210 kHz，较为接近波源信号中心频率(150 kHz)，其主要成分为由轴向振动引起的L(0,1)以及径向振动引起的F(1,2)、F(1,3)。且在较高频率区(450~570 kHz)产生了低幅值的T(0,2)；随着波的传导，在D点时，150 kHz附近的模态成分随声波衰减幅值有所下降，而在400~520 kHz区域产生了较高频的L与F混叠的模态；在声波传导至C点时，由于钢丝绳柱状结构的两端径向振动较大，声波的L(0,1)逐渐集中在250~350 kHz范围内并与F(1,2)、F(1,3)混叠在一起，150 kHz附近的模态成分主要为由质点径向振动引起的F模态。

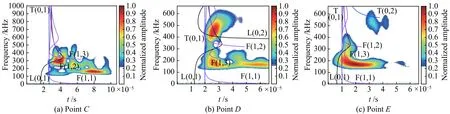
图12 150 kHz 端面近表面 AE 源信号时频与频散曲线叠加图Fig.12 Overlay of time-frequency and dispersion curves of AE source signal near the end-face center (Frequency: 150 kHz)

当端面中心设置频率为500 kHz的波源时，E点时频图的幅值较高区域在510~560 kHz，为T(0,2)和 F(1,4)，且在约 350、430 kHz 处产生了幅值较低的3种低阶模态的混叠，此时由F占据主导；当传播到D点时，较高频率(500~560 kHz)的模态成分幅值有所下降，而较低频率的模态成分幅值逐渐上升，L(0,1)与L(0,2)逐渐占据主导成分；声波传播到C点时，幅值较高区集中在320 kHz左右的L(0,1)，以及450 kHz的L与F混叠区域，在 500 kHz附近存在幅值较高的 T(0,2)和F(1,4)，但与初始相比其幅值有较大下降。

当激励源为500 kHz的端面近表面AE源信号时，E点的采样数据在约450 kHz存在少量的L(0,1)和 L(0,2)， 且 在 约 520 kHz处 T(0,2)和F(1,4)为该点的主要成分；在D点时 T(0,2)和F(1,4)两种模态仍占据主导，但在350~420 kHz产生的L(0,1)和L(0,2)幅值有所上升；在C点的450 kHz左右L模态幅值继续提高，但500 kHz附近的F模态仍为主要的模态成分。

当声发射源的位置在端面中心沿y轴激发时，150 kHz所产生的模态较少，主要为L纵向模态，且其特征频率与AE源信号的中心频率大致符合，同时存在少量的F模态，而T(0,1)与F(1,1)两曲线过于紧凑无法识别。500 kHz则产生了较高阶的F模态，在传导初始阶段仅有少量的L模态成分，随传播距离增加其幅值逐渐提高，为L与F共存的形式。

当声发射源的位置在端面中心沿x轴激发时，在导波传播的全过程中为F模态占据主导位置，这是由于x方向激励的波源使质点在径向上振动产生的。在频率较低时，L模态的幅值较高，且L与F主要为低阶模态，其特征频率也与信号中心频率相符。而在频率较高时，L模态幅值较低，其幅值随着导播传导有逐渐上升的趋势，但在导波传导至远端时，识别不同的模态成分较为困难。

表2为不同声发射源各采样点的特征频率值，可以看出，时频图中最高幅值区域所对应的特征频率基本对应声发射源中心频率，且由于频散现象会产生一些其他频率的较高幅值区。而根据高幅值区域上所覆盖的不同模态的频散曲线，可以得到各采样点的主要模态成分，发现当AE源在沿y轴激发时，模态成分主要为L纵向模态，当AE源在沿x轴激发时，模态成分主要为F弯曲模态。根据各点的主要模态成分构成以及所对应的特征频率，大致可以反映声发射源的中心频率和声发射源的类型。

表2 不同声发射源在各采样点的特征频率范围Table 2 Characteristic frequency range of different AE sources at each sampling point

3 结论

1）小波变换可以有效提取钢丝绳中损伤声发射源的时频特征，结合理论频散曲线可以有效识别声波的主要模态成分与各模态对应的特征频率。

2）不同位置、不同方向声发射源的时频图数据差别很大，沿x、y轴激发的AE源所体现出的主要模态成分不同，可根据设置多采样点所得数据进行时频分析，结合覆盖在高幅值区域的理论频散曲线可得到AE源信号的主要模态特征。经过分析，当AE源的主要模态为L纵向模态时，AE源为沿Y轴激发，当AE源的主要模态为F弯曲模态时，AE源为沿x轴激发，该方法可以判断钢丝绳中声发射源的不同振动方向与中心频率。